基于PPF控制算法对大型柔性多输入多输出板结构的主动振动控制研究

张 彭

(弗林德斯大学 科学与工程学院，南澳大利亚州 阿德莱德 5042)

大型柔性结构在很多领域有着广泛的应用，这种结构大多都有振动问题.大型柔性结构往往有无穷多的振动模态，而且其阻尼往往很小，很容易受到振动的影响.控制器设计的复杂程度随着受控对象的阶数增加而急剧增长，一般设计控制器时只考虑目标频率范围内的共振点.但是根据降阶模型设计出的控制器，往往在控制高阶受控系统时会产生溢出，从而造成整个闭环系统的不稳定[1].为了消除溢出对闭环系统造成的影响，人们提出很多新型的控制算法.其中，最常使用的控制算法包括:谐振控制[2],独立模态空间控制[3]和正位置反馈控制(PPF控制)[4].

谐振控制是基于谐振系统的特性产生的控制算法[5].设计谐振控制器时，对于每个模态的增益选择是独立的，可以节省很多计算量，加快控制器的设计速度[6].而且一组传感器作动器可以控制多个振动模态，有利于谐振控制扩展到更大型的结构中.然而谐振控制无法给系统提供很大的阻尼，在某些系统中其控制效果往往无法达到要求[4].

独立模态空间控制最早由Meirovich提出，它对每个受控模态使用一组模态滤波器防止系统溢出[3].独立模态空间控制最大的弊端在于每一个受控模态需要由一组传感器作动器控制，且其控制器的设计需要很高的计算量，因此其往往无法运用于大型结构中.

PPF控制最初由Goh和Caughey提出[4].PPF控制器是一个二阶低通滤波器，可以有效的减少溢出.PPF在很多结构中有广泛的运用[7-8].和另外两种控制算法相比，PPF可以给系统提供更大的阻尼效果，且一组传感器作动器可以控制多个振动模态[9].

基于以上的分析，可以设计一种基于PPF控制算法对大型柔性多输入多输出板结构的主动控制器.通过系统建模求得板结构的数学模型，运用PPF控制算法设计出控制器结构.通过闭环系统稳定条件，求得控制器最优参数.模拟和实验数据表明控制器的减振效果可达20 dB以上，可大幅提高系统的减振性能.

1 系统建模

本文中的实验系统由两块板组成，如图1.顶板(400 mm×400 mm×1.5 mm)由三组扩音器(传感器/作动器)固定在底板上.实验过程中，干扰信号由干扰传感器持续输入到底板上，引起顶板的振动.控制目标是在底板持续振动时，保持顶板稳定.

图1 大型柔性多输入多输出板结构实验设置

图2 开环系统建模

对多输入多输出板状柔性结构设计有效的控制器，需要建立受控对象的数学模型.为了建立有效的属性模型，本文先进行了开环系统的研究.信号发生器产生的正弦信号u1,u2,u3分别单独的输入T1，T2和T3,三路输出信号y1,y2和y3同时由NI DAQ 9234读取，加上输入信号，四路信号将被送入ModalView进行信号处理，如图2所示.产生系统的频率响应方程为：

(1)

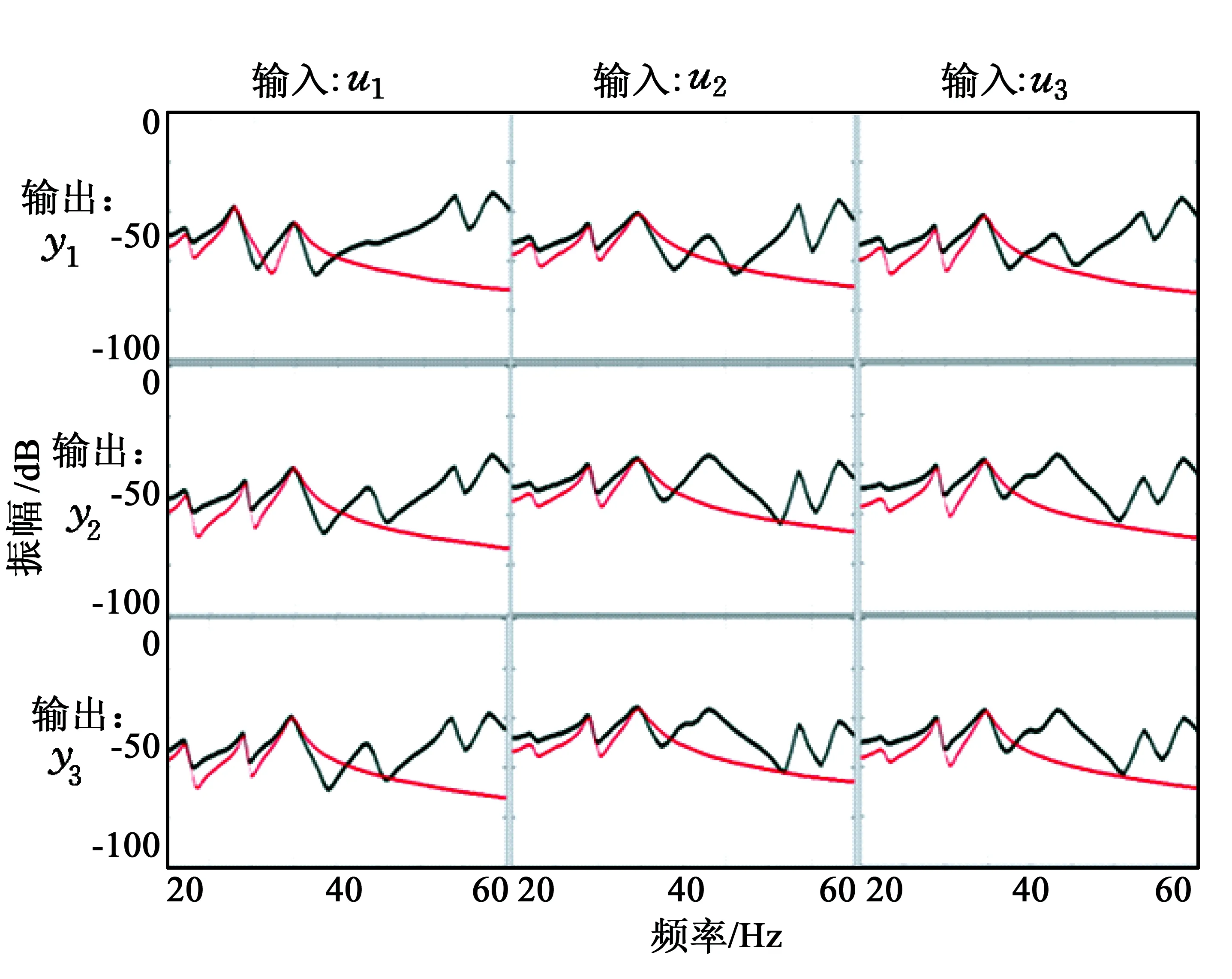
图3 系统建模实验数据及简化模型

实验所得的3×3系统频率响应如图3黑线所示.为了得到受控对象的数学模型，本文使用多维多项式曲线拟合法求解系统各振动模态对应传递函数Hijs对应的参数:

(2)

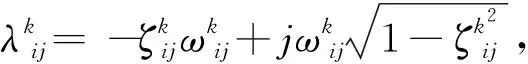
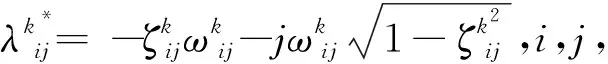
(3)

对于此系统而言，目标频率范围为20～40 Hz，包含了前3个振动模态.因此，系统数学模型可以简化为图3中虚线：

(4)

2 PPF控制器设计

PPF控制算法最早由Goh和Caughey提出[4]，整个系统由两部分组成.第一部分代表了系统结构方程，另外一部分代表PPF控制器方程，系统结构图如图4：

结构方程:

(5)

Y(t)=ψX(t)

(6)

控制器方程:

(7)

U(t)=(CΩc)Gη(t)

(8)

式中X和η分别代表系统和控制器的模态向量，

定义η=G-1/2ξ， 系统方式(5)～(8)可写为：

(9)

根据二阶系统稳定性理论[4]，系统闭环稳定需满足：

(10)

即：

Ω2-ψTCGCψ>0

(11)

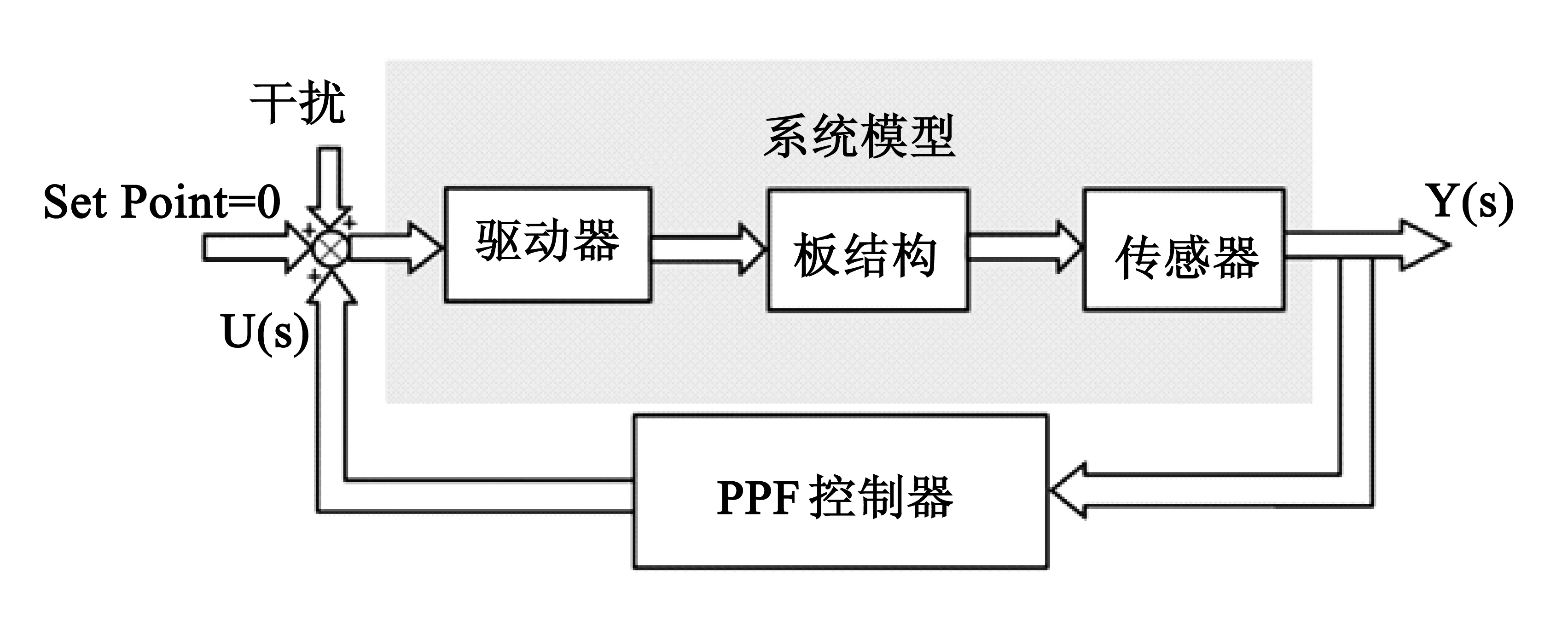
图4 闭环系统结构图

为了给系统增加阻尼，从而实现减振效果，控制器的频率Ωc需要设置为系统频率(Ωc=Ω)[10].控制器阻尼范围为(0,1)，为了保证控制器鲁棒性，一般PPF控制器阻尼范围设置成(0.5,1).控制器增益矩阵的最优化选取需根据系统稳定性条件(11)决定.为了得到PPF控制器控制效果最优化参数组合，定义Hij-Cl(s)(i,j= 1,2,3)为系统闭环频率反馈方程.通过遗传算法求得Hij-Cl(s)的H无穷最小值：

(12)

从而获得Dc,Ωc,和G最优解.

3 模拟和实验结果

使用第二章通过遗传算法所得最优PPF控制器参数组，在MATLAB SIMULINK中对此多输入多输出大型柔性板结构进行模拟仿真，并得到如图5的控制结果.图中，黄色曲线为开环系统频率响应，粉色曲线为系统闭环PPF控制效果曲线.仿真结果表明，系统闭环PPF控制效果大幅度减少振动幅值约19.850 dB(减少89.826%).

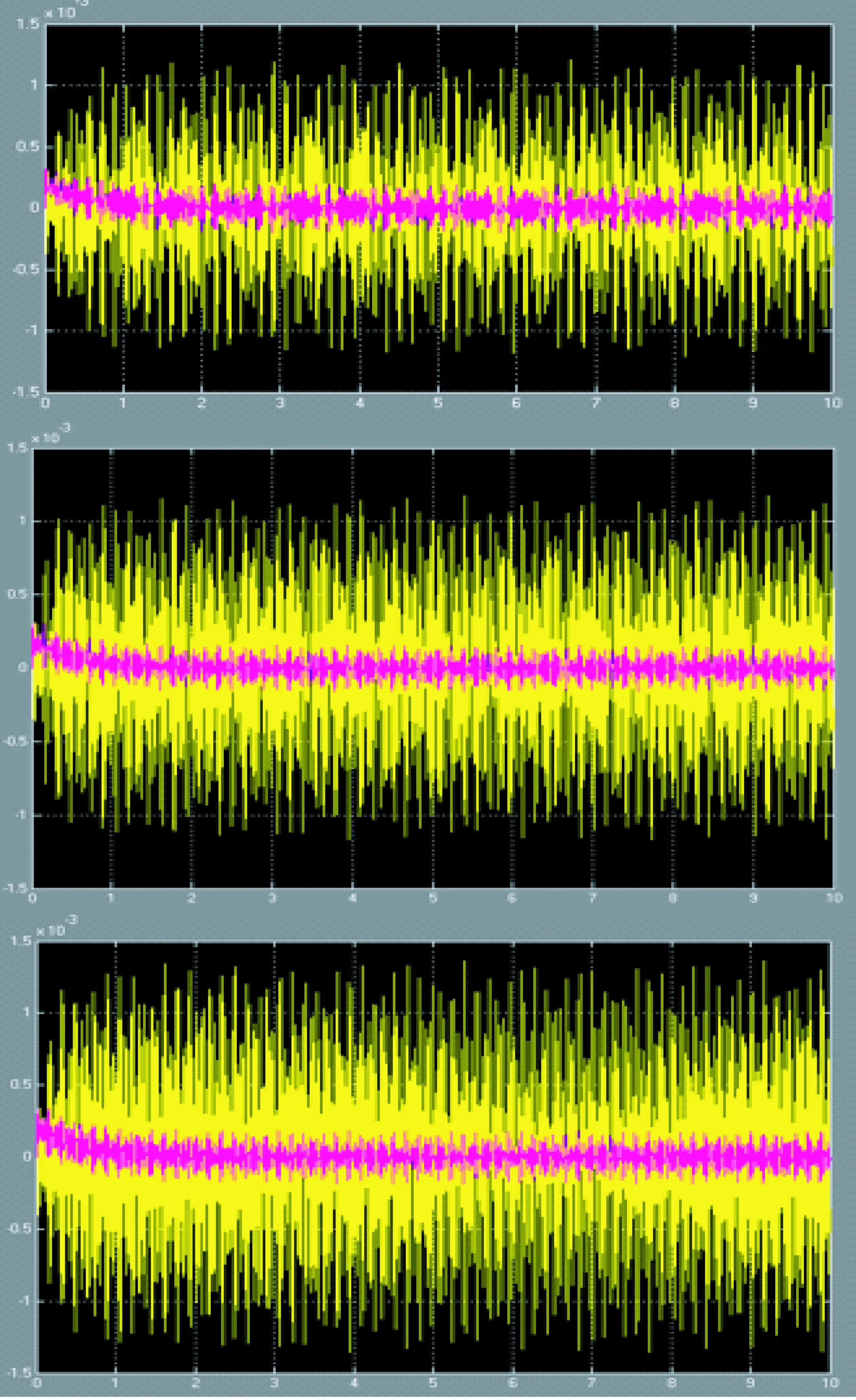
图5 模拟仿真结果

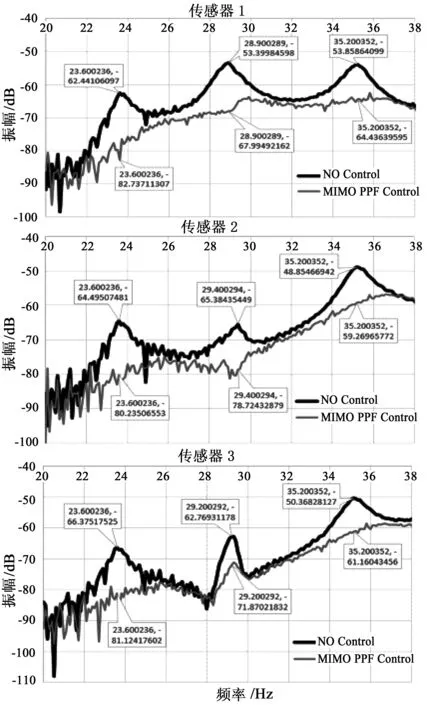
图6 实验结果

多输入多输出实验设置如图1所示.干扰由信号发生器产生输入至干扰传感器.顶板上的三组加速度传感器的感应信号作为输入信号传递至DSPACE，开环系统频率反馈如图6深色曲线.图6浅色曲线表示闭环系统PPF控制效果频率反馈曲线.由表1数据可得，系统第一振动模态在三组传感器/作动器位置平均减振16.928 dB，第二振动模态平均减振12.345 dB，第三振动模态平均减振10.595 dB.由此可见，实验结果和仿真结果均表明本文提出的多输入多输出PPF控制对于大型柔性板结构减振效果显著，大幅度的减少了原系统振动幅度，从而保证了系统在振动干扰情况下的安全性.

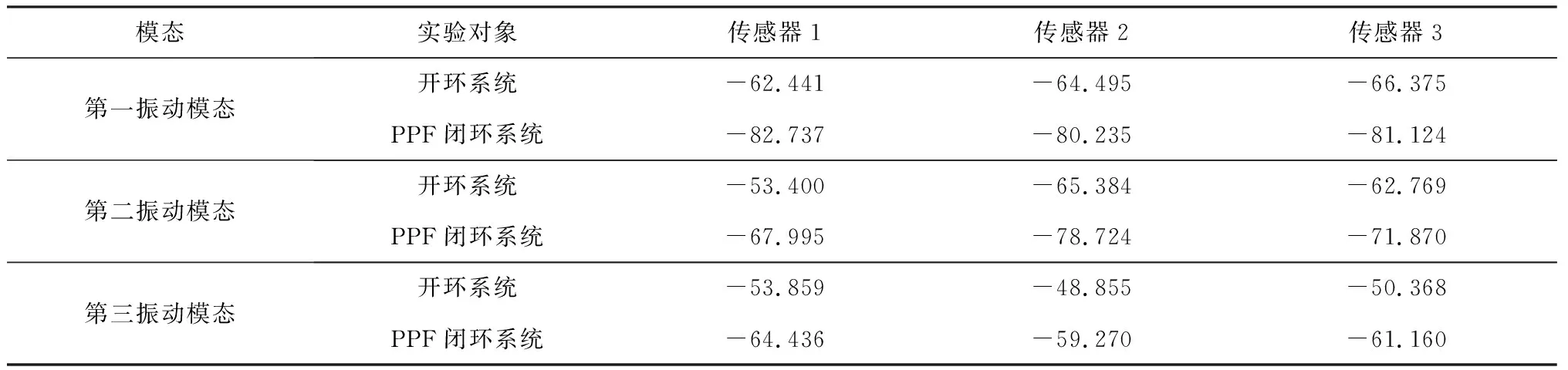
表1 系统实验数据/dB

4 结语

研究针对大型柔性板结构的振动问题，提出了基于PPF控制算法的多输入多输出主动控制振动研究.通过遗传算法求得闭环传递函数H无穷最小值的方法，得到多输入多输出多振动模态PPF控制器参数最优解并成功通过系统模拟仿真和实验验证了PPF控制器的有效性.提出的PPF控制方法可以进一步拓展到更大的柔性结构中并运用于更宽的频率范围.