压电陶瓷振动传感器的迟滞非线性误差补偿研究
陈高华, 闫献国, 郭 宏, 李志飞
(1.太原科技大学 电子信息工程学院,太原 030024;2.太原科技大学 机械工程学院,太原 030024)
机械设备的振动信号可直接反映其当前的工作状态,以航空飞行器为例, 据统计70%以上的发动机故障可以通过振动形式表现出来[1]。因此,可以通过监测振动信号来分析、推测、判断设备内部一些组件的工作状况。
因具有良好的压电效应、较高的居里温度、强自发极性、高机电耦合系数、亚纳米级分辨率以及亚微秒级的响应时间,压电陶瓷在微驱动、微测量领域中得到了广泛研究与应用[2-5]。比如使用压电陶瓷材料制成的振动传感器被用于飞机发动机故障诊断上,可以用来测量累积性损伤,裂纹增长,转子不平衡[6]。但是压电陶瓷本身存在迟滞,蠕变,非线性等特性,直接影响到传感器的检测精度[7-8]。其中迟滞特性的影响最大,因此迟滞非线性补偿成为提高基于压电陶瓷传感的微测量精度的首要问题。为减小或消除该不利影响,可以利用逆模型进行线性化控制[9-10],而利用逆模型进行线性化控制的关键是非线性迟滞的精确建模。
描述压电陶瓷迟滞现象的经典建模方法大体分为两类:一类是根据压电陶瓷的微观机理建立物理方程,从而求解出输入输出关系的建模方法[11-12]。另一类是只考虑输入输出关系而不深究其微观机理的建模方法,包括 Preisach模型[13]、Prandtl-Ishlinskii 模型(简称PI模型)[14]、多项式模型[15]、Bouc-Wen模型(简称B-W模型)[16-17]等。其中B-W模型由于只需要用一个辅助的非线性微分方程来描述迟滞行为,计算效率高,实时性好,且逆模型求解十分方便,因而受到更多研究者的青睐。传统B-W模型是一个关于中心点严格对称的模型,而压电陶瓷的迟滞特性是不完全对称的,所以传统B-W模型很难达到较高的拟合精度。
本文在压电陶瓷压电效应的理论基础上,研究了电荷放大器在压电陶瓷传感系统中的应用,分析了压电陶瓷传感器迟滞非线性产生的原因。在传统B-W模型的基础上,提出了改进算法,建立了压电陶瓷传感器的非对称迟滞模型,并给出了模型参数对迟滞曲线的影响关系和逆模型的求取方法。设计实验,利用改进Bouc-Wen逆模型补偿压电陶瓷传感器的迟滞非线性,验证了所提方法的有效性。
1 压电陶瓷传感器的基本性能
1.1 压电陶瓷传感器的压电效应
压电陶瓷的正压电效应是指介质在力的作用下产生形变,引起介质表面带电,逆压电效应是指施加激励电场,介质将产生机械变形。压电陶瓷传感器是一种基于压电陶瓷材料的正压电效应而工作的功能器件。压电陶瓷的正压电效应示意图如图1所示。压电陶瓷材料经极化处理后,剩余极化强度会使与极化方向垂直的两端出现束缚电荷(一端为正,另一端为负),由于这些束缚电荷的作用会使压电陶瓷的两个电极表面产生极性相反的自由电荷,并使整个压电陶瓷片呈电中性。当外界压力使压电陶瓷材料发生变形时,瓷片压缩,极化强度变小,导致上下表面的电势改变,和表面接触的两电极上的部分自由电荷被释放,因此在电路中会有电荷流动。

图1 压电陶瓷正压电效应示意图
1.2 电荷放大器
压电陶瓷传感器的输出信号非常微弱,且电荷在电路中易消耗掉,所以在使用时通常与电荷放大器配合使用,把电荷信号Q转换成电压信号U完成物理量的测试。
电荷放大器的工作原理如图2所示,图中Q为压电陶瓷传感器受到外力后产生的电荷量,Ci为输入级等效电容(包括传感器等效电容、连接电路等效电容和放大级输入电容),Ri为输入级等效电阻(包括传感器等效电阻、连接电路等效电阻和放大级输入电阻)Cf为反馈电容,Rf为反馈电阻。

图2 电荷放大器工作原理图
设运算放大器的开环增益为A,则输出电压
u0=-Aui
(1)
根据集成运算放大器工作在线性区域的虚断特点,对运放的反向输入端对应结点列写KCL方程,可以得到如下关系
(2)
由式(1)和式(2)可得
(3)
式(3)相应的相量式为
(4)
当运放的开环增益大于105时,上式可简写为
(5)
以上所述的分析结果表明,电荷放大器输出电压相量和输入电荷相量的比值大小决定于被测信号的振动频率和反馈网络的参数,如果测量信号的振动频率相当高时,可以得到
(6)
即:电荷放大器输出电压U0与采集到的电荷Q近似成正比关系。
1.3 迟滞非线性成因分析
压电陶瓷是属于铁电材料的压电体,未经预极化处理的压电陶瓷材料,是一种多晶体多电畴材料,对于其中的每个电畴来说,具有方向相同的自发极化,但就由多晶体多电畴组成的整体而言,因各电畴无规则排列,各电畴的极化效应被相互抵消,并不具有压电效应。如图3(a)所示。压电陶瓷自发极化的电畴会在外电场的作用下重新取向,这种在外电场作用下,电畴重新取向的状态称为铁电效应[18]。为使压电陶瓷材料具有压电效应, 就必须利用其铁电效应进行预极化处理,即在压电陶瓷上加一足够高的直流电场,并保持一定的温度和时间,迫使其电畴转向,或者说迫使其自发极化作定向排列。如图3(b)所示。去掉电场后,经预极化处理后的电畴虽然不会完全转向与电场一致的方向,但在压电陶瓷内部仍存有很强的剩余极化强度。如图3(c)所示。当外界机械力F作用于压电陶瓷传感器时,会使压电陶瓷材料发生形变,压电陶瓷材料的形变迫使电畴发生转向,极化强度变小;当减小外界机械力F,压电陶瓷材料恢复形变,极化强度变大,而非180°电畴转向是不完全可逆的,相对于形变增加的过程中,减小过程电畴转向要比同一应变时增加过程时的电畴转向要小,因此极化强度小于同一应变时形变增加时的极化强度。从而压电陶瓷传感器的应变-输出电压曲线产生严重的迟滞非线性现象。

(a) 极化处理前 (b) 极化处理过程中 (c) 极化处理后
图3 压电陶瓷的极化处理
Fig.3 Polarization treatment of the piezoelectric ceramic
2 非对称迟滞模型建立
压电陶瓷传感器的迟滞非线性可以利用逆模型进行线性化控制,本文在传统B-W模型的基础上,提出一种改进模型来表征压电陶瓷传感器的非对称迟滞特性。模型建立包括两部分:①正模型建立,正模型建立主要是确立压电陶瓷传感器的输出电压随驱动位移变化的模型关系;②逆模型求取,逆模型求取主要是对所建立的正模型进行反变换,得到压电陶瓷传感器的驱动位移随输出电压变化的模型关系。
2.1 正模型建立
根据传统B-W模型,电压u(t)的表达式定义为
u(t)=dx(t)+h(t)
(7)
式中:x(t)是迟滞输入,u(t)是迟滞输出,d为传感器输出电压与驱动位移的比率常量,h(t)代表一个可观测的迟滞非线性项。在零初始条件下,h(t)满足如下方程[19]
(8)
式中:α,β,γ和n用来控制迟滞回线的形状大小。式(8)可进一步改写为
(9)
定义形状控制函数为
Ψ(x′,h)=γ+βsgn[x′(t)h(t)]
(10)
其中sgn表示符号函数。
由式(10)可知:传统B-W模型的形状函数在四个不同的区域只有两个独立的值(γ+β和γ-β),它是关于中心点严格对称的模型, 因而,如果直接用它描述压电陶瓷的非对称迟滞现象,很难达到较高的拟合精度。
为了提高模型精度,对传统B-W模型进行改进势在必行, 且改进型B-W模型的形状控制函数必须具有非对称性。为使改进后的B-W模型的形状控制函数在其四个区域段具有相互独立的值,本文定义形状控制函数为
(11)
如图4所示,本文改进B-W模型的形状控制函数在四个区域段具有四个独立的值:①在区域段(x′≥0,h≥0),ψ(x′,h)的值为γ+β+φ;②在区域段(x′<0,h≥0),ψ(x′,h)的值为γ-β-φ;③在区域段(x′<0,h<0),ψ(x′,h)的值为γ+β-φ;④在区域段(x′>0,h<0),ψ(x′,h)的值为γ-β+φ。

图4 改进B-W模型的形状控制函数特性
由于改进B-W模型的形状控制函数在四个区域段具有四个独立的值,能够独立地控制迟滞回线在四个区域段的形状,所以改进后B-W模型既可以描述对称迟滞,也可以描述非对称迟滞现象。
2.2 模型参数分析
(1) 令d=1,α=1,β=1,γ=0.5,φ=0.5,n=1,输入x(t)=2sint,传统B-W和改进B-W的迟滞正模型曲线,如图5所示。
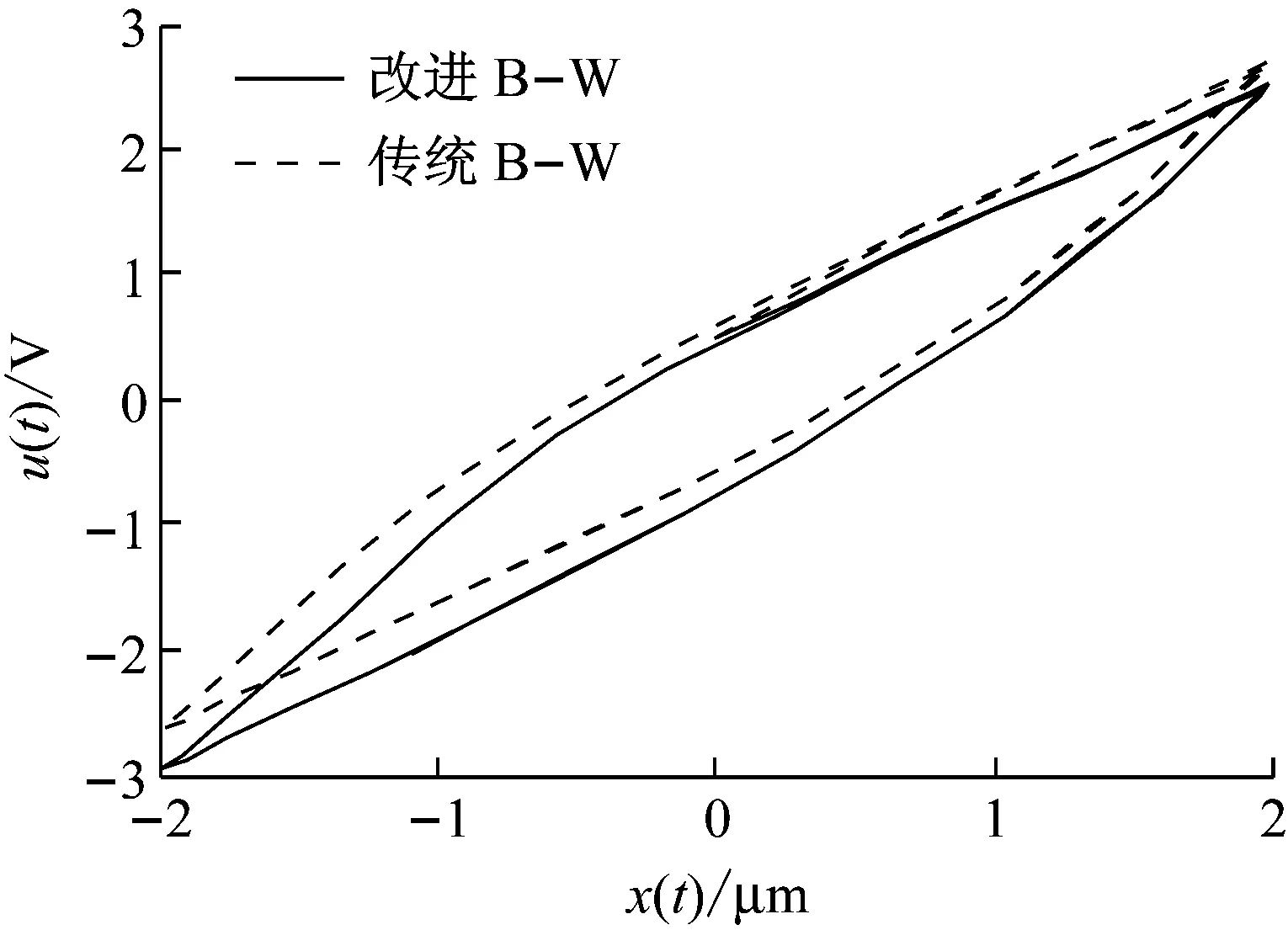
图5 迟滞正模型曲线
(2) 令d=1,β=1,γ=0.5,φ=0.5,n=1,输入x(t)=2sint,当α=0.6和α=2时改进B-W的迟滞正模型曲线,如图6所示。
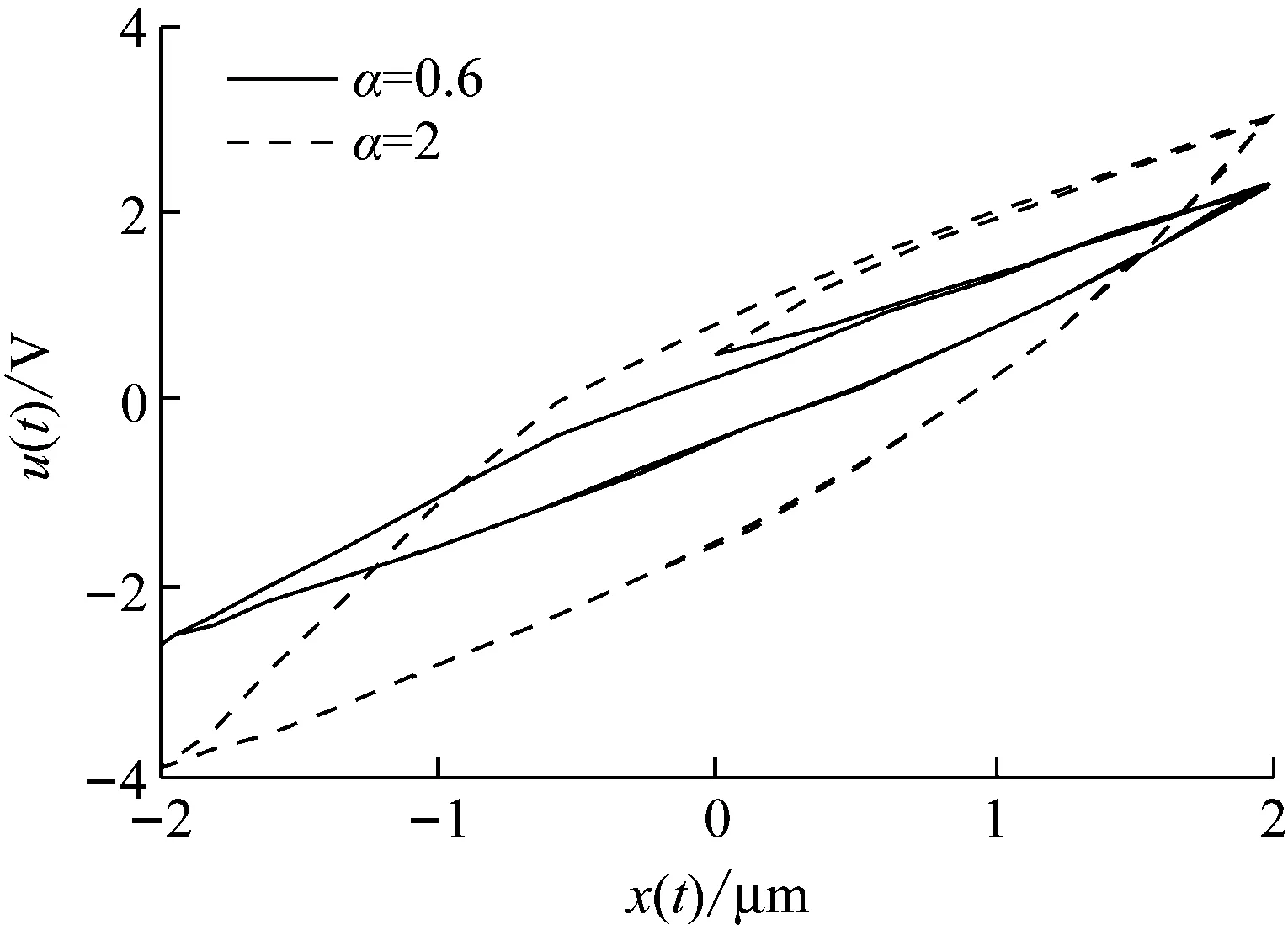
图6 α改变时迟滞曲线
(3) 令d=1,α=1,γ=0.5,φ=0.5,n=1,输入x(t)=2sint,当β=0.6和β=2时改进B-W的迟滞正模型曲线,如图7所示。

图7 β改变时迟滞曲线
(4) 令d=1,α=1,β=1,φ=0.5,n=1,输入x(t)=2sint,当γ=0.6和γ=2时改进B-W的迟滞正模型曲线,如图8所示。

图8 γ改变时迟滞曲线
(5) 令d=1,α=1,β=1,γ=0.5,n=1,输入x(t)=2sint,当φ=0.05和φ=0.5时改进B-W的迟滞正模型曲线,如图9所示。

图9 φ改变时迟滞曲线
(6) 令d=1,α=1,β=1,γ=0.5,φ=0.5,输入x(t)=2sint,当n=0.1和n=1时改进B-W的迟滞正模型曲线,如图10所示。

图10 n改变时迟滞曲线
(7) 令d=1,α=1,β=1,γ=0.5,φ=0.5,n=1,输入x(t)=2sint和x(t)=2sin 10t时改进B-W的迟滞正模型曲线,如图11所示。

图11 频率改变时迟滞曲线
由图5可以看出:传统B-W模型是关于中心点对称的,本文提出的改进B-W模型可以反映非对称迟滞特性。由图6~图10可以看出:改变参数α,β,γ,φ和n的值时,迟滞曲线的形状和大小会随着改变。其中,参数α主要影响迟滞曲线的大小,对迟滞曲线的形状和非对称特性影响不大;参数β,γ,φ和n的大小主要影响迟滞曲线的形状和非对称特性。由图11可以看出:当输入信号的频率改变时,迟滞曲线也会随着改变,即,本文提出的改进B-W模型可以反映频率相关性。
2.3 逆模型求取
对式(7)求取反函数可得
(12)
由2.1节可知,改进B-W正模型的迟滞非线性项h(t)在零初始条件下满足如下关系
h′(t)=x′(t){α-[γ+βsgn(x′(t)h(t))+

(13)
其中
(14)
定理 对于由式(12)和式(13)描述的改进Bouc-Wen迟滞逆模型,有
sgn(x′)=sgn(u′)
证明 对于式(13)描述的非线性动态系统
h′(t)=x′(t){α-[γ+βsgn(x′(t)h(t))+

由Gronwall定理可知,h(t)有界,且
(15)
故
(16)
由式(12)得
(17)
式中:d为传感器输出电压与驱动位移的比率常量,d≥0。
由式(16)、(17)可知

(18)
即:sgn(x′)=sgn(u′)
(19)
定理得证。
由式(12)~式(14)和定理可得
(20)
h′(t)=x′(t)f(u′,h)
(21)
与图5对应的迟滞逆模型曲线,如图12所示。

图12 改进 B-W迟滞逆模型曲线
3 迟滞逆补偿实验
本文利用改进B-W逆模型作为补偿器来补偿压电陶瓷传感器的迟滞非线性。
3.1 改进B-W模型参数辨识
3.1.1 实验装置
在辨识模型参数前需要通过实验测试得到一组压电陶瓷传感器的输入输出数据,然后利用该数据进行参数辨识。实验测试装置如图13所示。本研究首先由测试平台产生一个正弦信号,经过驱动电源放大处理,输出给压电陶瓷位移驱动器(0~150 V,55 μm),压电陶瓷位移驱动器控制加压板产生正弦波振动载荷施加给PZT压电陶瓷传感器,传感器产生的电荷信号由电荷放大器转换为电压信号。最后,电荷放大器的输出电压信号和位移传感器获得的位移信号通过数据采集卡传送给上位机。

图13 实验装置
3.1.2 模型参数辨识
本文提出的改进B-W模型有6个需要辨识的参数,它们分别是d,α,β,γ,φ和n。目前,辨识模型参数的方法有很多,如最小二乘法、粒子群算法、差分进化算法等。其中,差分进化算法待定参数少,收敛速度快,不易陷入局部最优,具有较强的全局收敛能力和鲁棒性[20]。故本文采用差分进化算法进行模型参数辨识, 算法流程如图14所示。
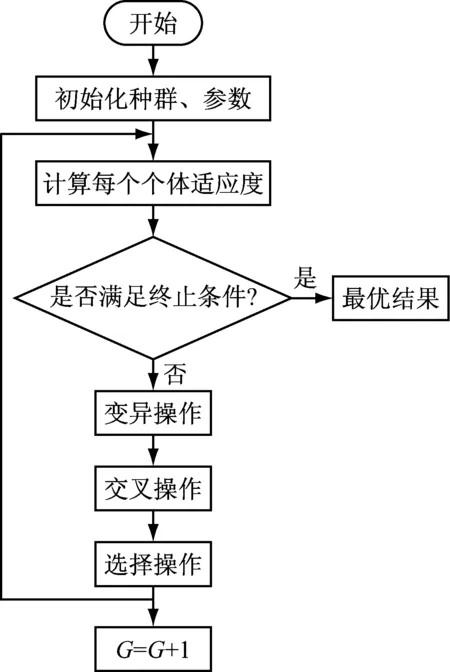
图14 参数辨识算法流程
算法运行中,取种群规模M=50,最大迭代次数G=200,变异因子F=0.8,交叉因子CR=0.6,辨识误差指标为
(22)
辨识误差函数J的优化过程如图15所示,最终误差指标为:J=4.406 6×10-9。根据实验数据辨识得到的模型参数如表1所示。改进B-W模型与实验测得的数据对比如图16所示,模型曲线和实验曲线基本吻合。
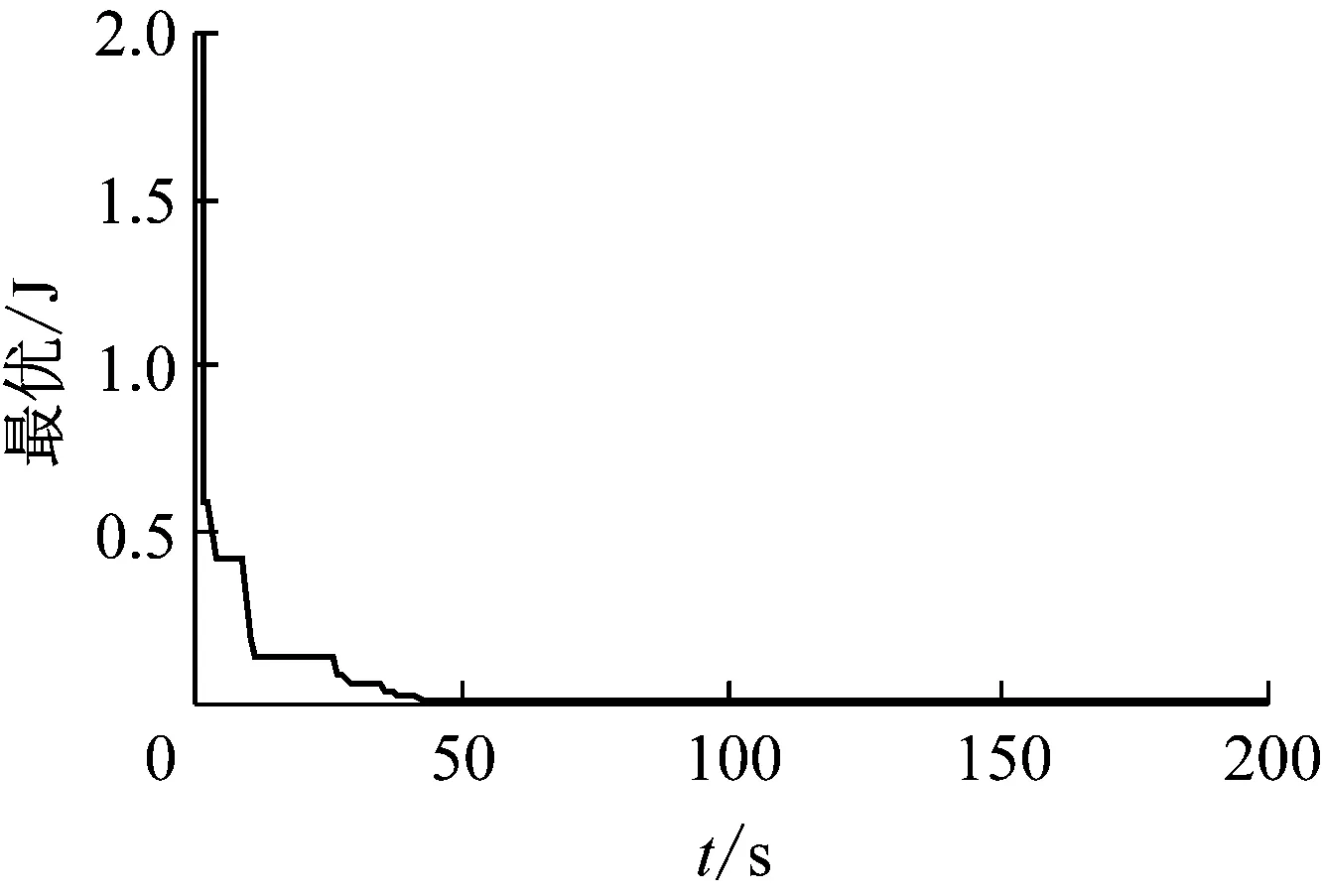
图15 误差函数的优化过程

参数数值d/(V·μm-1)4.263α/(V·μm-1)1.902β/(μm-1)0.785γ/(μm-1)-0.210ϕ/(μm-1)0.075n1.005

图16 改进B-W模型和实验数据对比
3.2 迟滞逆补偿
为了测试改进B-W逆模型对压电陶瓷传感器的迟滞非线性补偿效果,将表1中根据实验数据辨识得到的模型参数代入逆模型进行补偿验证,实验流程如图17所示。

图17 传感器迟滞逆补偿流程
Fig.17 The hysteresis inverse compensation processing of sensors
经传统B-W迟滞逆模型补偿校正后,压电陶瓷传感器的校正位移与输入位移的特性曲线见图18,跟踪误差曲线见图19,最大跟踪误差为0.29 μm。经改进B-W迟滞逆模型补偿校正后,压电陶瓷传感器的校正位移与输入位移的特性曲线见图20,跟踪误差曲线见图21,最大跟踪误差为0.03 μm。由图18~图21可以看出:通过逆补偿后,改进B-W模型的跟踪误差远小于传统B-W模型的跟踪误差。即,经改进B-W模型逆补偿后,校正位移总是能够很好跟踪传感器的实际输入位移,跟踪误差小于0.03 μm,有效保证了传感器的检测精度。

图18 传统B-W模型补偿后的跟踪特性曲线

图19 传统B-W模型补偿后的跟踪误差曲线
Fig.19 The tracking error curve after compensation of traditional B-W model

图20 改进B-W模型补偿后的跟踪特性曲线
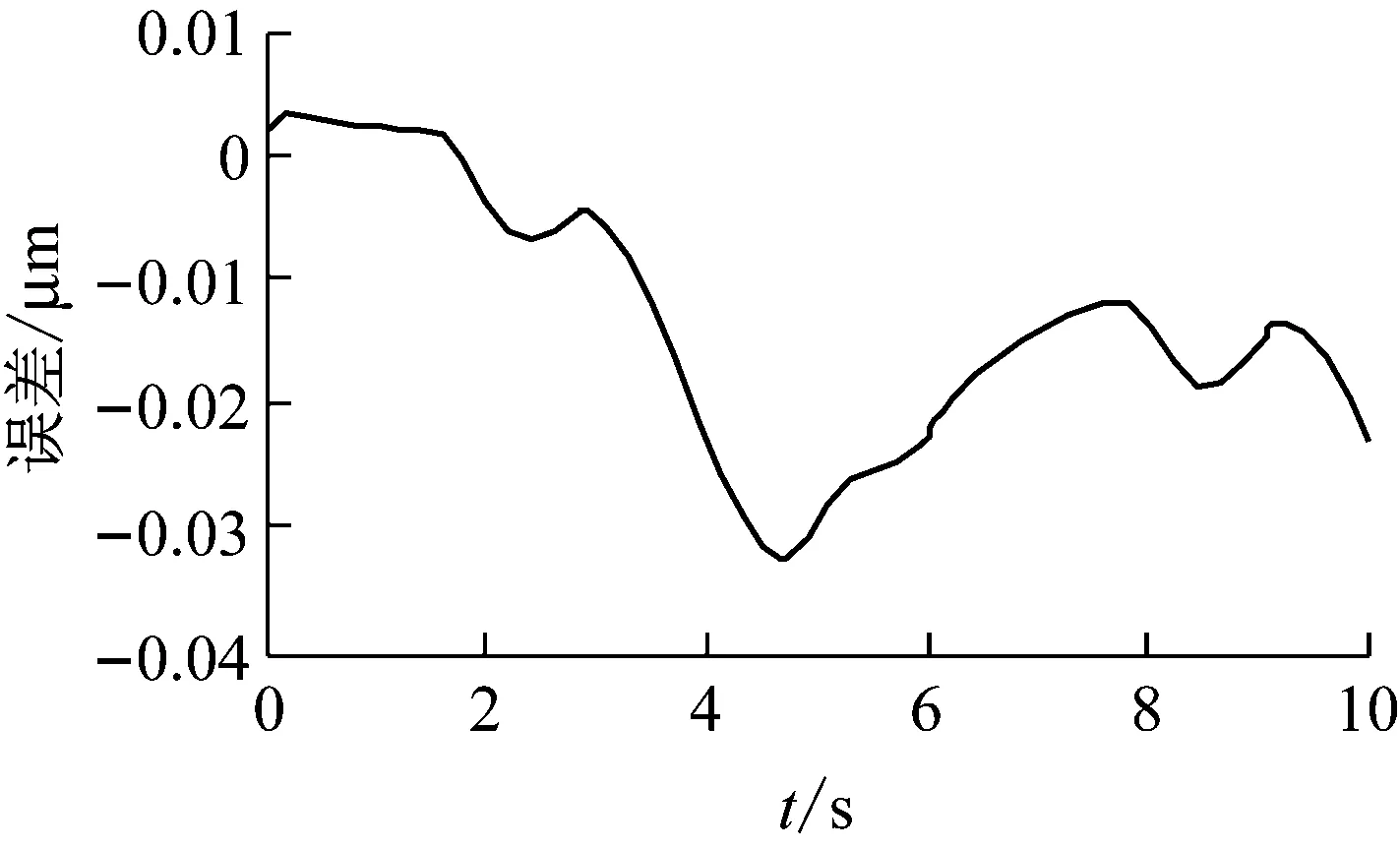
图21 改进B-W模型补偿后的跟踪误差曲线
4 结 论
压电陶瓷的迟滞非线性是影响压电陶瓷微测量系统检测精度的主要因素。本文通过分析压电陶瓷的铁电效应微观极化机理,确定了压电陶瓷传感器产生迟滞非线性现象的原因。针对传统B-W模型不能准确反映压电陶瓷传感器的非对称迟滞特性而导致检测精度难以提高的问题,提出了一种可以表征压电陶瓷传感器非对称迟滞现象的改进B-W模型,研究并给出了模型参数对迟滞曲线的大小、形状及平稳性的影响关系和逆模型的求取方法。在正弦波振动载荷下,分别利用传统B-W逆模型和改进B-W逆模型作为补偿器补偿压电陶瓷传感器的迟滞非线性,实验结果显示,经改进B-W模型逆补偿之后,校正位移总是能够很好跟踪传感器的实际输入位移,而且跟踪误差明显小于传统B-W模型的跟踪误差,有效保证了检测精度。本文研究成果为基于压电陶瓷传感器的振动测试系统提供了一种有效的迟滞非线性误差补偿方法,且适用于具有迟滞特性的其它类型传感器。

