永磁电机驱动的刮板输送机主传动系统机电耦合扭振动态分岔研究

鞠锦勇， 李 威， 范孟豹, 王禹桥， 杨雪锋

(1.中国矿业大学 机电工程学院，江苏 徐州 221116； 2.安徽工程大学 机械与汽车工程学院，安徽 芜湖 241000)

近些年来，在国家“去产能”和“调结构”的宏观调控下，确保煤矿开采的安全性以及高产高效变成了其首要任务[1]。现阶段，传统的刮板输送机传动系统为了实现软启动以及具有较强的过载能力，在异步电机和减速器之间增加液力偶合器、限矩摩擦离合器、调速偶合器等软启动装备，这类机电传动方式传动线路长，传动环节多，很容易出现诸多故障，并且齿轮传动系统还需保证良好的润滑[2-3]。在高效率、高可靠性以及大功率的发展趋势下，传统的异步电机驱动系统面临着不少挑战[4]。

在国家节能减排号召下，“变频永磁直驱”成为各行业重点攻克的新课题[5-7]。随着矢量控制和直接转矩控制在交流调速系统中的不断发展和完善，近年来在风力发电[8-9]、装备制造[10-11]、电动汽车[12-13]、船舶推进[14]、矿业牵引等传统采用异步电机的领域不断可见交流永磁电机的应用。Haring等[15]指出交流永磁电机在很宽的速度范围内具有高的响应性能和灵活性，使得永磁直驱概念对于大部分的实际应用是可行的。采用大功率永磁电机直接驱动工作装置，实现 “近零传动”，能够显著提高系统运行效率以及降低故障率，是现今大功率机电装备的发展趋势[16]。但是，由于刮板输送机主传动系统(机头)是一个多质量弹性连接的机械动力学系统，在运输作业时所施加负载力矩和电动机电磁转矩的联合作用下，将使系统连接轴产生扭转振动。并且采用大功率永磁电机直接驱动刮板输送机机头滚筒，省去了中间传动机构，系统连接轴所承担的电磁转矩与负载力矩将会显著变大，其扭转振动现象将更加明显[17-18]。因此为了确保大功率永磁电机在刮板输送机上的安全可靠运用，首先需要对刮板输送机主传动系统扭转动态特性进行分析。

在分析刮板输送机主传动轴系这类相对转动运动系统时，多数学者将其等效为质量弹性扭转系统。Duan等[19]对含摩擦、间隙和裂纹的转子系统研究时发现系统出现亚临界Hopf分岔是导致主传动系统发生自激振动的主要原因；刘彬等[20]将轧机主传动系统等效为转子-轴承相对转动系统，并基于非线性反馈控制对系统分岔进行了控制；刘爽等[21]考虑时滞非线性参数的影响，分析了一类相对转动系统的Hopf分岔特性；Das等[22]采用多尺度法分析了一类柔性转子-轴承相对转动运动系统的扭转振动特性，并提出通过控制电磁驱动器以提高系统临界转速。上述研究较好地从机械参数角度，研究了摩擦、间隙、外部负载等因素对相对转动运动系统扭转动态特性的影响，但是忽略了电气系统对系统动态特性的影响。由于永磁电机作为整个系统的直接动力源，其输出电磁转矩直接作用在相对转动系统连接轴上，必然对系统连接轴动态特性产生较大影响。孟杰等[23]基于机电系统分析动力学，对高速电主轴电机-主轴系统进行了局部耦合和全局耦合分析，并据此分析了该系统的机电耦合动力学特性；熊万里等[24]建立了异步电机-转子系统的机电耦合模型，并采用数值计算研究了负载波动及串联补偿电容引起的系统机电耦合非平稳过渡过程；Kia等[25]分析了一类感应电机-变速箱机电系统，讨论了齿轮箱轴系扭振对感应电机电流及转矩的影响；田拥胜等[26]针对一台高速永磁电机设计了电磁轴承转子系统，并对该系统进行了动力学性能分析与实验测试研究。但是由于机械参数与电气参数之间复杂的非线性耦合关系，上述研究主要是通过数值仿真进行分析，对于电机系统与相对转动转子系统的机电耦合特性还有待进一步深入研究，从而有利于相对转动系统的安全平稳运行。

本文以交流永磁电机驱动的刮板输送机主传动系统为研究对象，考虑刮板输送机作业过程中运输煤物料质量不均匀性产生的非线性摩阻，基于拉格朗日-麦克斯韦原理[27]，建立了刮板输送机主传动系统机电耦合非线性扭振动力学模型，研究非线性摩阻转矩系数变化时系统表现的复杂动力学行为，重点分析系统的Hopf分岔形式及运动稳定性。这对大功率永磁电机在刮板输送机上的有效利用，以及刮板输送机主传动系统的安全稳定运动具有非常重要的意义。

1 系统机电耦合动力学建模

构成永磁电机驱动的刮板输送机主传动系统主要包括：大功率交流永磁电机、连接轴、工作滚筒等部件。可将这些传动部件归纳为两种，一种质量大而弹性小，如电动机、滚筒等；另外一种弹性大而质量小，如连接轴等。因此为了更好地分析永磁电机驱动下刮板输送机主传动系统的扭振特性，从全局机电耦合角度，将系统等效为一个由若干惯性部件和弹性部件构成的“质量弹性系统”，最终构建了永磁电机-刮板输送机机头滚筒的物理模型，如图1所示。图1中，J1，J2分别为永磁电机输出轴转动惯量与刮板输送机机头滚筒转动惯量；K，C分别为连接轴扭转刚度与阻尼系数；θ1，θ2分别为永磁电机转角及刮板输送机机头滚筒转角；ia，ib，ic分别为永磁电机三相定子电流；ua，ub，uc分别为永磁电机三相定子输入电压；永磁电机电磁转矩为Tm；刮板输送机机头滚筒负载转矩为Tl。建模过程中做如下假设： ①磁饱和及永磁体损耗忽略不计，各相绕组的自感和互感都是线性的；②永磁电机转子无偏心，气隙均匀；③忽略温度和频率变化对电动机参数的影响。

图1 永磁电机-刮板输送机机头滚筒运动物理模型

(1) 首先确定永磁电机驱动的刮板输送机主传动系统广义坐标共5个，如表1所示。其中电磁系统包括3个分别为永磁电机三相定子电量，机械系统包括2个分别为永磁电机转角与刮板输送机机头滚筒转角。

表1永磁电机驱动的刮板输送机主传动系统广义坐标

Tab.1Generalizedcoordinatesofthemaindrivesystemofthescraperconveyordrivenbypermanentmagnetmotor

广义坐标电磁系统定子转子j=1j=2j=3-机械系统电机转角滚筒转角j=4j=5qjeaebecΨfθ1θ2q·jiaibic---θ·1θ·2Qjuaubuc---F11F22

(2) 系统广义动能包括机械系统运动动能和电磁系统磁场能。其中，永磁电机驱动的刮板输送机主传动机械系统的动能主要包括：电机轴转动动能、滚筒转动动能，可表示为

(1)

永磁电机的磁场能主要包括定子电流产生的磁能以及永磁体转子产生的磁链与定子电流作用产生的磁能，可表示为

(2)

式中：La，Lb，Lc分别为永磁电机三相定子绕组自感系数；H为永磁电机三相定子绕组互感系数。

(3) 系统势能为连接轴扭转变形所致的弹性势能，取弹性力形式为：Fk=K(θ1-θ2)，则系统势能可表示为

(3)

(4) 系统耗散函数包括电磁系统和机械系统两部分，可表示为

(4)

式中：Ra，Rb，Rc分别为永磁电机三相定子绕组电阻。

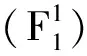
(5)

将式(1)～式(5)代入拉格朗日-麦克斯韦方程

(6)

式中：Ll为拉格朗日算子，可表示为

Ll=Emech+Wm-U

(7)

对于定子绕组A(j=1)，取q1=ea，将式(7)代入式(6)可得定子绕组A的电压方程为

(8)

同理，对于定子绕组B(j=2)和定子绕组C(j=3)，电压方程可分别表示为

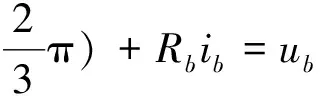
(9)

(10)

对于机械系统，当取广义坐标为电机转角(j=4)，即q4=θ1，式(7)代入式(6)可得永磁电机转角的运动方程为

(11)

同理可得刮板机机头滚筒转角的运动方程为

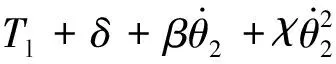
(12)

联立式(8)～式(12)，可得永磁电机驱动的刮板输送机主传动系统机电耦合扭振动力学模型为

Rbib=ub

Rcic=uc

(13)

(14)

式中：ud，Id分别为永磁电机定子直轴电压与电流；uq，Iq分别为永磁电机定子交轴电压与电流。

2 平衡点的稳定性及Hopf分岔存在性分析

刮板输送机在作业过程中，由于运输煤物料质量的不均匀性会导致滚筒与拖链间摩阻力矩的变化，继而导致系统发生Hopf分岔，并伴随有失稳振荡。因此选取摩擦因数β为分岔参数。用[x1x2x3x4x5]T代替[IdIqϑω1ω2]T，式(14)可化为

(15)

式中：A(x,β)为原系统的Jacobian矩阵，f(x,β)为原系统的非线性项。

式(15)的平衡点通过适当的坐标变换可以转移到坐标原点，因此研究系统平衡点在原点处的动力学特性具有普遍意义，选择合适的参数得式(15)在原点处Jacobian矩阵和非线性项为

(16)

式(16)特征方程可表示

κ5+λ1κ4+λ2κ3+λ3κ2+λ4κ1+λ5=0

(18)

由A(0,β) 特征根的实部可判定式(15)在原点处的稳定性，如果A(0,β)特征根有正实部，则系统在原点处不稳定，将出现失稳振荡；若A(0,β)特征根的实部全部为负，则系统在原点处渐进稳定；当A(0,β)特征根有零实部时，此时需要考虑系统非线性项f(x,β)的影响。传统的方法是根据原系统相关参数计算其Jacobian矩阵A(0,β)的所有特征根，进而判断参数变化时A(0,β)是否有特征根穿越虚轴，该方法计算量大，且很难写出系统特征根跟分岔参数β的解析表达式。故本文利用Hurwitz判据判定原系统Hopf分岔的存在。原系统在原点Jacobian矩阵的特征方程其系数λi可构成如下Hurwitz行列式

(19)

式中：如果i>5，则λi=0。系数Λi(i=1～5)由分岔参数β确定。基于Hurwitz判据判定原系统Hopf分岔存在性及计算相应分岔参数值的具体流程，如图2所示。

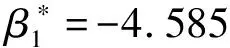
图2 永磁电机驱动的刮板输送机主传动系统扭振Hopf分岔存在性判定流程

3 系统模型降维及分岔类型判定

(20)

式中：J为永磁电机驱动的刮板输送机主传动系统线性化矩阵的Jordan标准型，f(Y)为非线性部分。将相关参数代入，可得f(Y)的表达式为

f(Y)=inv(T)f(TY,β)=

根据f(Y)表达式，可以看出原系统标准型方程非线性部分不仅与中心流形参量y1，y2有关，而且与稳定流形参量y3，y4有关。因此为了实现对原系统的降维，根据中心流形定理可设

(21)

c11=-0.081 64χ，c12=-0.002 097χ，

c15=-0.050 25χ，

c21=-0.220 63χ，c22=0.002 550χ，c25=-0.200 47χ

31.373y2+F1(y1,y2)+U1(y1,y2)

-31.487 8y1+F2(y1,y2)+V1(y1,y2)

(22)

式中：U1(y1,y2)与V1(y1,y2)为含y1，y2的高阶项。

25.264y3+F1(y2,y3)+U2(y2,y3)

-25.264y2+F2(y2,y3)+V2(y2,y3)

(23)

式中：U2(y2,y3)与V2(y2,y3)为含y2，y3的高阶项。

根据局部不变流形与中心流形定理知，式(22)，式(23)与式(14)的非线性特性相同，在平衡点处具有相同的稳定性及分岔类型。根据规范型理论，可得原系统二阶中心流形Hopf分岔稳定性指标为

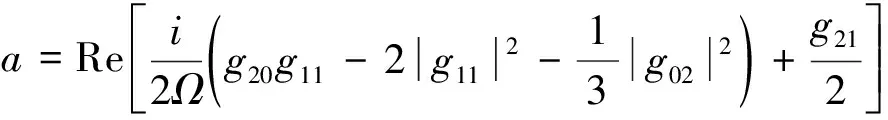
(24)

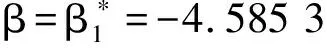
a=0.095 268χ2>0

(25)

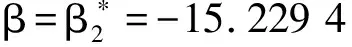
a=-0.025 918χ2<0

(26)

由式(25)、式(26)知，当一次线性摩阻系数β=-4.585 3，永磁电机驱动的刮板输送机主传动系统在平衡点(0,0)发生亚临界Hopf分岔，当一次线性摩阻系数β=-15.229 4，永磁电机驱动的刮板输送机主传动系统在平衡点(0,0)发生超临界Hopf分岔，并且系统在临界点发生的Hopf分岔类型与系统所受平方项摩阻系数(χ)无关。

4 数值仿真验证

图3 超临界Hopf分岔时电机转速-机头滚筒转速相图(β=-13)

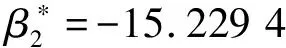
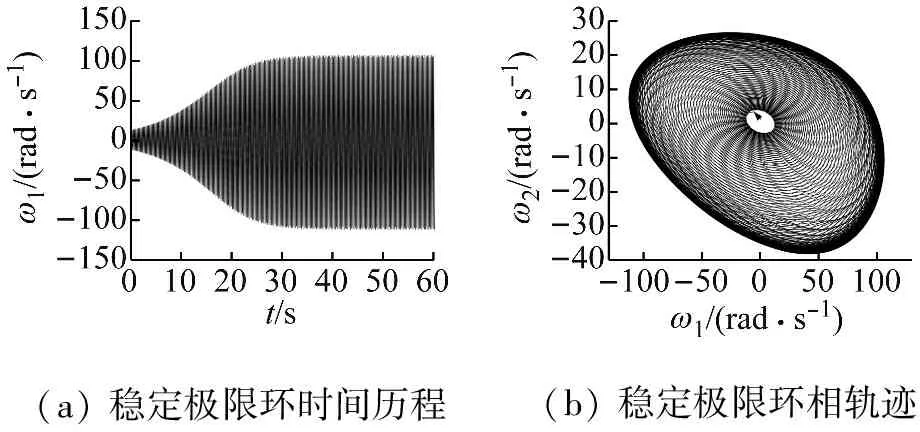
(a) 稳定极限环时间历程(b) 稳定极限环相轨迹

图4 超临界Hopf分岔时电机转速-机头滚筒转速曲线(β=-16，初值为[0.5,0.5,0.5,0.5,0.5])

Fig.4 Response curve of motor speed and drum speed in supercritical Hopf bifurcation (β=-16, initial condition is [0.5,0.5,0.5,0.5,0.5])

(a) 稳定极限环时间历程(b) 稳定极限环相轨迹

图5 超临界Hopf分岔时电机转速-机头滚筒转速曲线(β=-16，初值为[1,1,1,1,1])

Fig.5 Response curve of motor speed and drum speed in supercritical Hopf bifurcation (β=-16, initial condition is [1,1,1,1,1])

图6 亚临界Hopf分岔时电机转速-机头滚筒转速相图(β=-7)

Fig.6 Phase diagram of motor speed and drum speed in subcritical Hopf bifurcation (β=-7)

(a) 稳定极限环时间历程

(b) 稳定极限环相轨迹

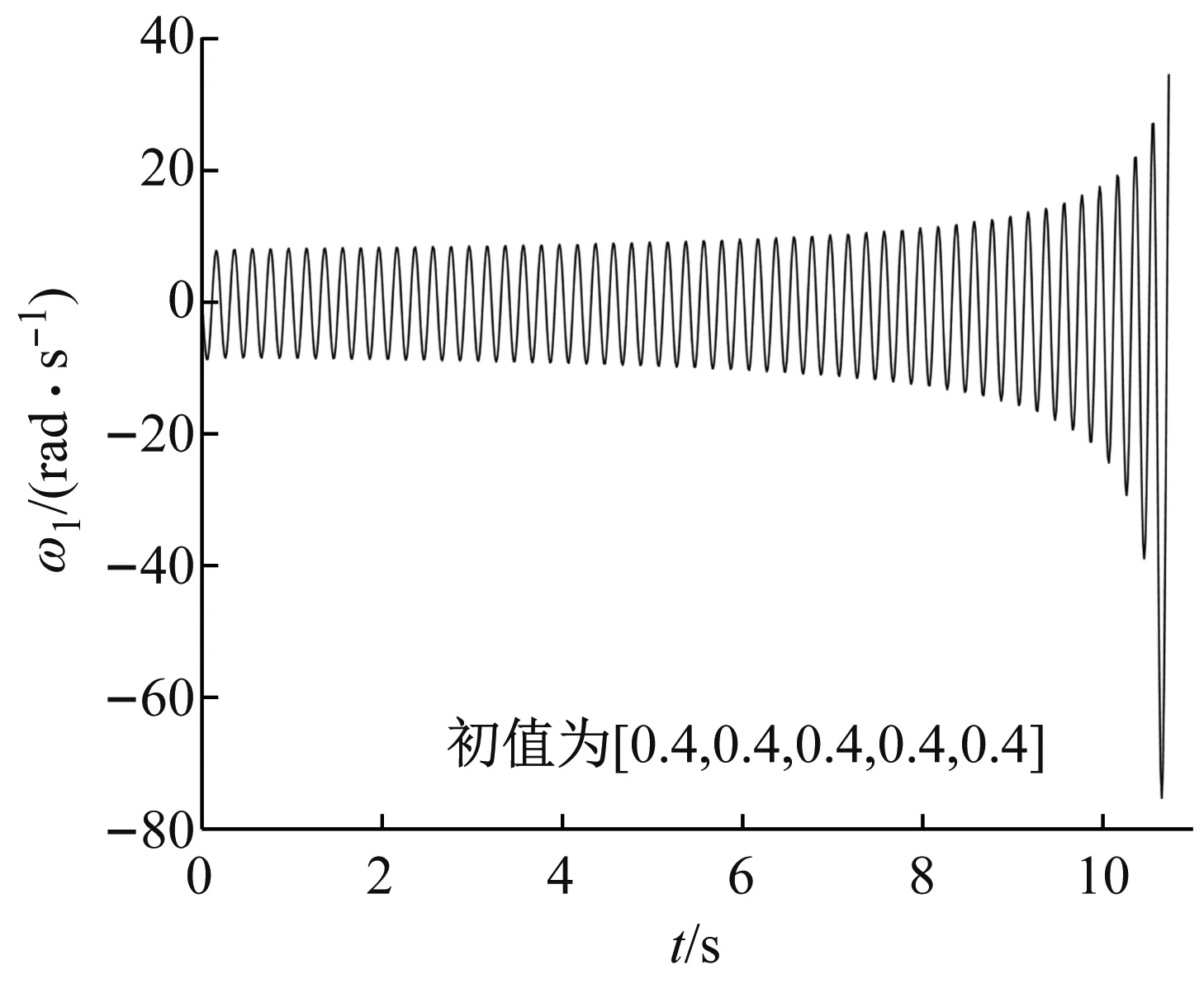
(c) 不稳定极限环时间历程

(d) 不稳定极限环相轨迹

综合文中分析结果可知，永磁电机驱动的刮板输>送机主传动轴系Hopf分岔临界点位置由系统线性部分决定，因此，后期进行大功率永磁电机控制器设计时，可结合文中方法对控制器线性增益部分进行设计，扩大系统的稳定范围并将系统具有潜在威胁的亚临界Hopf分岔控制为超临界Hopf分岔，保证刮板输送机系统的稳定运行。

5 结 论

本文考虑大功率永磁电机直接驱动形式下刮板输送机作业过程中运输煤物料质量的不均匀性，建立了一类非线性摩阻作用下刮板输送机主传动系统的机电耦合非线性扭振动力学模型，利用中心流形理论与规范型理论对刮板机主传动系统扭振Hopf分岔行为进行解析分析。理论分析与数值仿真计算结果表明：

(3) 将大功率永磁电机应用到刮板输送机上，应该考虑运输煤物料质量不均匀性的影响，具体应用时应避免在系统亚临界Hopf分岔临界点附近工作，根据本文的分析结果，可为后期刮板输送机主传动系统亚临界Hopf分岔的控制研究提供参考。