桥梁地震需求分析中建模不确定性的敏感性研究

吴文朋， 李立峰， 唐盛华， 张旭辉

(1. 湘潭大学 土木工程与力学学院，湖南 湘潭 411105；2. 湖南大学 土木工程学院，长沙 410082; 3. 工程结构动力学与可靠性分析湖南省高等学校重点实验室，湖南 湘潭 411105)

基于性能的抗震设计(Performance Based Seismic Design,PBSD)理论自提出以来就得到了各国学者的重视，经过20多年的发展，尽管其优点已被广泛认可，且分析理论已经逐渐成熟，但在实际应用中完全基于性能的桥梁抗震设计案例并不多。这主要是由于当前的PBSD方法大多建立在全概率可靠度理论基础之上[1]，而如何合理地识别、量化和吸收各种相关的不确定性，是推动性能抗震设计向实际工程应用转化的关键[2]。

桥梁概率地震需求分析(Probabilistic Seismic Demand Analysis,PSDA)是PBSD的重要中间环节之一。早期的桥梁地震需求分析大多只考虑影响相对较突出的地震波不确定性[3-4]。Mackie等[5]的研究表明，地震波和桥梁建模相关的不确定性都会对桥梁结构的地震需求产生较大影响。尽管有些研究对桥梁建模相关的不确定性考虑得比较充分[6-7]，但没能定量地分析这些不确定性因素对桥梁地震需求的影响程度。

Pan等[8]分析了5种不确定性参数对桥墩地震响应的影响，指出上部结构重量和支座摩擦因数的影响较大。Tubaldi等[9]研究了23种不确定性在PSDA中的传递效果，指出结构建模相关不确定性的影响不可忽略。Padgett等[10]将桥梁地震响应相关的不确定性分为地震波、桥梁宏观尺寸和桥梁建模相关三大类，并进行了比较分析，研究结果表明与桥梁宏观尺寸相关的不确定性对桥梁区域性地震易损性分析的影响最大。Wang等[11]针对采用美国新抗震规范进行设计的加州地区的桥梁，分别研究了地震波不确定性和建模不确定性的影响，得到的结论是，尽管桥梁建模不确定性远小于地震波的不确定性，但有必要考虑两类不确定性的耦合效应。Pang等[12]采用均匀设计方法同时考虑多种不确定性因素的影响，研究表明考虑所有不确定性时的桥梁失效概率要大于只考虑一种不确定性时的桥梁失效概率。

以上研究都强调了桥梁建模相关不确定性在桥梁地震需求分析中的重要性。理论上讲，考虑的不确定性因素越多，则对桥梁地震需求的预测越准确。然而，实际工程中影响桥梁抗震分析的建模相关不确定性因素有很多，如果考虑全部不确定性的影响，会导致非线性时程分析的计算量很大，而且并非每种不确定性的影响权重都一样。因此，有必要对PSDA中的各种桥梁建模相关不确定性的影响进行敏感性研究，以确定重要的不确定性参数。本文以采用我国新规范设计的某多跨钢筋混凝土连续梁桥为例，同时考虑与结构材料、边界条件和桥梁结构相关的三类不确定性因素，并基于OpenSEES源代码程序建立了参数化有限元模型，输入22条标准化的远场强震地震波进行非线性动力分析，基于条带概率分析方法和龙卷风图对各种不确定性进行了敏感性研究，得到这些不确定性对桥梁地震需求分析的影响规律，并给出了影响较大的重要不确定性参数。

1 算例桥梁有限元建模

算例桥梁为一座4×30 m的连续梁桥，上部结构由8片T梁组成，桥面宽19 m，材料为C40；中间桥墩是由3个直径1.4 m的圆柱和盖梁组成的排架式桥墩，墩高均为10 m，材料为C30；桥墩截面沿环向布置30根纵筋，配筋率1.6%；采用螺旋式箍筋，体积配箍率0.6%，纵筋和箍筋的材料均为HRB335。桥墩盖梁处设置8个型号为GJZ 450×450×114的普通板式橡胶支座；桥台采用桩基支承的座式桥台，且采用铅芯橡胶支座；桥墩盖梁和桥台处在横桥向均采用了滑移混凝土型挡[13-14]。

基于OpenSEES源代码分析平台[15]建立桥梁有限元模型。主梁采用弹性梁单元模拟；墩柱采用弹塑性纤维梁单元模拟，其中混凝土和钢筋的应力-应变关系分别采用Concrete 04 和Steel 02材料，模型参数来自Mander模型和Menegotto-Pinto模型；支座均采用Elastomeric Bearing Element模拟；桥台模拟考虑了台后填土和桩基的双重贡献，采用Hyperbolic Gap Material和Hysteretic Material并联模拟；挡块采用徐略勤和李建中提出的滑移型挡块力学模型进行模拟；桥台处的碰撞采Impact Material进行模拟。本文不考虑桥墩处桩-土相互作用的影响。以上各个构件的力学模型如图1所示。

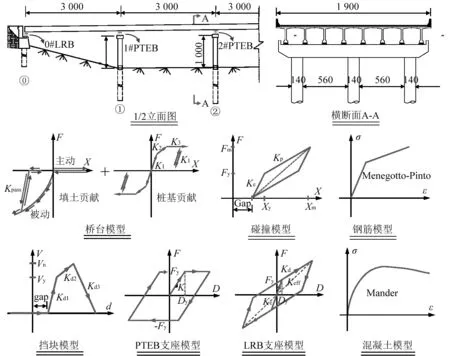
图1 算例桥梁有限元模型(单位：cm)Fig.1 Finite element model of the bridge (unit: cm)

2 桥梁建模不确定性参数

影响桥梁结构地震需求分析的不确定性可分为认知不确定性和偶然不确定性，其中，认知不确定性是由于人类当前撑握的知识或信息不够充分导致的，而偶然不确定性是事物自身固有的属性，在实际工程中二者的区别并不明显。例如，混凝土本构参数的不确定性是材料的固有属性，但结构自重、支座参数是由于缺乏足够的信息所致。由于这些不确定性都体现在桥梁结构有限元建模中，本文统一归于建模相关的不确定性。此外，阻尼比的不确定性也归类于桥梁建模相关的不确定性。本文主要从结构层次、材料层次和边界条件3个方面进行展开。

2.1 结构层次不确定性

结构层次的不确定性(Structural Uncertainty, SU)主要影响结构整体的动力特性和响应。从结构动力学的角度来讲，与质量矩阵、刚度矩阵以及阻尼矩阵相关的不确定性都可归于这一类，但本文主要考虑与构件宏观尺寸以及阻尼比等相关的不确定性。

桥梁工程施工现场的复杂性以及混凝土配制过程存在的偶然误差，都会导致桥梁上部结构和桥墩等构件的几何尺寸和密度存在差异，从而影响桥梁结构的质量分布以及刚度特性。Nielson等在研究美国中部和东南地区的桥梁地震易损性时，假定结构的质量调整系数服从U(0.9,1.1)的均匀分布。Pan等在研究美国纽约地区的桥梁地震易损性时，假定上部结构的容重系数服从U(0.8,1.3)的均匀分布。Ellingwood等[16]通过对结构的恒载进行统计分析后，建议结构抗震分析中恒载服从正态分布，均值为1.05倍的设计容重，变异系数为10%。于晓辉[17]在研究我国钢筋混凝土框架结构地震易损性时，比较了国内文献对混凝土容重变异性的差别，并建议混凝土容重为服从正态分布的随机变量，均值为μc=26.5 kN/m3，标准差为σc=1.75 kN/m3。我国《公路桥桥涵设计通用规范》[18]建议在设计中钢筋混凝土的容重为25～26 kN/m3。综合考虑，本文假定主梁和桥墩容重的中值为25 kN/m3, 容重系数λw服从正态分布N(1.04, 10%)，如表1所示。质量分布则随容重变化而变化。由于桥墩在地震作用下的非线性特性与其直径(D)、保护层厚度(c)以及纵筋直径(d)等有关，因此，根据既有的研究，本文假定这些参数也服从正态分布，分布特性如表1所示。

结构在地震作用下的各种非线性滞回响应或永久变形都将耗散一定的能量，而在结构非线性分析过程中的能量耗散是通过定义阻尼比(ξ)来实现的，且阻尼比的定义也有利于数值计算的收敛和稳定。我国《公路桥梁抗震设计细则》[19]规定混凝土结构的阻尼比可取ξ=0.05。本文采用基于质量和刚度的Rayleigh阻尼，参考Nielson等的研究，假定阻尼比服从正态分布，分布特征如表1所示。

2.2 材料层次不确定性

材料层次的不确定性(Material Uncertainty, MU)主要影响桥墩在地震作用下的非线性响应。由于上部结构和盖梁采用弹性梁单元模型，因此本文主要考虑墩柱纵向钢筋HRB335和混凝土C30两种材料的不确定性，箍筋不确定性的影响则通过约束混凝土本构模型的变异性来体现。

桥梁抗震分析中混凝土的本构常采用Mander模型，因此本文采用OpenSEE中相对应的Concrete 04材料来模拟。混凝土材料又以箍筋为界分为非约束混凝土(保护层)和约束混凝土(核心区)。OpenSEES对于Concrete 04材料的定义涉及多个参数，本文不考虑混凝土的抗拉效应，因此主要涉及4个参数：峰值应力、峰值应变、极限应变以及初始切线弹性模量。由于Mander模型中约束和非约束混凝土的初始切线弹性模量相同，因此，共有7个混凝土材料参数需要考虑，根据既有的研究，本文假定这些参数均服从对数正态分布，分布特征如表1所示。

桥墩纵向钢筋的本构采用Steel 02材料，选取钢筋屈服强度(fy)、弹性模量(Es)和强屈比(B)3个参数为随机变量，且均服从对数正态分布。墩柱纵向钢筋采用HRB335级钢筋，其相应的抗拉强度标准值为fyk=335 MPa，根据我国2010版《混凝土设计规范》[20]的规定，钢筋的强度平均值(fym)与强度标准值(fyk)之间应该满足关系式fyk=(1-1.645δy)fym(95%保证率)，其中，δy为钢筋的抗拉强度变异系数，对于HRB335级钢筋，δy=7%。我国规范对钢筋弹性模量(Es)和强屈比(B)的变异性没有相应的规定，因此，本文根据以往的研究成果假定这两个参数的随机分布特征如表1所示。

2.3 边界条件不确定性

算例桥梁考虑了支座、桥台、挡块以及碰撞等复杂的非线性力学特性，这些非线性特征在桥梁结构的地震分析中十分析重要，因此有必要考虑边界条件不确定性(Boundary Uncertainty, BU)的影响。

普通板式橡胶支座(Plate-Type Elastomeric Bearing,PTEB)的力学模型由其弹性剪切刚度K以及临界摩擦力Fy决定。其中，弹性剪切刚度K变异性主要取决于橡胶材料的剪切刚性模量G，临界摩擦力Fy的变异性则取决于支座的轴力和摩擦因数。我国常用板式橡胶支座中橡胶材料剪切弹性模量GPTEB服从正态分布[21]。因此，假定橡胶支座的弹性剪切刚度服从正态分布，分布特征如表1所示。李冲等[22]的试验研究表明，板式橡胶支座与混凝土表面接触时，其摩擦因数(μ)与支座竖向应力N成反比。当N=4 MPa时，摩擦因数在0.3～0.4；当N=6 MPa时，摩擦因数在0.2～0.3；当N=8 MPa时，摩擦因数在0.15～0.25；当N=10 MPa时，摩擦因数在0.1～0.25。由于本文不考虑竖向地震动，支座承担的竖向轴力变化很小，本文直接以恒载作用下的支座反力为竖向压力，根据此竖向力可假定支座的摩擦因数μPTEB服从均匀分布U(0.15,0.25)。

铅芯橡胶支座(Lead Rubber Bearing,LRB)是在普通板式橡胶支座的基础之上发展起来的一种有阻尼特性的隔震支座。铅芯橡胶支座所用的铅必须是高纯度而无杂质的铅，因此铅芯的变异性较小。地震作用下铅芯屈服以后的水平刚度几乎为零，此时支座水平刚度主要由橡胶层承担。因此可以假定铅芯橡胶支座的屈服后刚度KP_LRB为服从正态分布的随机变量，同PTEB一样，其分布特征也取决于橡胶材料的剪切弹性模量，如表1所示。铅芯橡胶支座初始刚度取为屈服后刚度的6.5倍。

桥台模型同时考虑了台后填土以及桩基的贡献，因此，桥台模型既有主动刚度又有被动刚度，其力学模型如图1所示。对于被动土压力的影响，本文采用Shamsabadi等[23]提出的双曲线力-位移模型(Hyperbolic Force-Displacement,HFD)，HFD模型的相关参数有平均刚度(KA)、极限承载力(Pult)以及最大位移(ymax)。在OpenSEES程序中可用Hyperbolic Gap Material(HGM)来模拟HFD，而HGM默认的参数是初始切线刚度，桥台建模时需要将平均刚度换算成初始切线刚度。桥台主动水平刚度主要由桩基础提供，以单根桩的等效水平刚度KActive为基准，本文以三折线滞回模型模拟桩基的贡献。以桥台被动初始切线刚度KPassive、极限承载力Pult以及单桩等效水平刚度KActive为随机变量，参考Nielson等的研究，本文假定3个随机变量均服从U(0.5R,1.5R)的均匀分布，R表示参考既有研究成果计算出的3个随机变量的理论值，其具体分布特征如表1所示。

表1 建模相关不确定性参数Tab.1 Modeling related uncertainty parameters

挡块是钢筋混凝土桥梁横向主要的限位和传力构件之一。算例桥梁在桥台和墩顶处都设置了横向挡块，挡块的形式均采用徐略勤等推荐的新型滑移型钢筋混凝土挡块，他们根据大量的试验研究提出了三折线的挡块模型简化计算公式，如图1所示。本文仅考虑简化模型中钢筋混凝土挡块的屈服力Vy和极限力Vn的不确定性，由于桥台和墩顶处的挡块配筋形式相同，只是挡块底面的剪切面积不同，因此桥台和墩顶处挡块的不确定性可同时用竖向剪切钢筋的屈服强度(fyv)和极限强度(fuv)的变异性来表示，其分布特征如表1所示。对于挡块与主梁之间的间隙(δ)的设计，目前没有统一的规定，本文假定δ服从均匀分布U(3,10)。伸缩缝是设置在主梁与桥台背墙之间的间隙，正常使用状态该间隙能够适应温度变化、制动力以及收缩徐变等引起的主梁位移。目前对于伸缩缝间隙(Δ)的设计也没有统一规定，本文假定Δ服从均匀分布U(5,15)。需要说明是的，尽管本文对δ和Δ假定带有一定的主观性，但取值范围均参考了既往的研究成果和一些实际桥梁工程的设计经验，以此来探讨δ和Δ的不确定性对桥梁抗震分析的影响是可行的。地震作用下主梁的位移可能会足够大，以致伸缩缝完全闭合，进而引起主梁与桥台之间发生碰撞，一般可取主梁的轴向刚度为碰撞有效刚度，即Keff=EA/L，其中E为混凝土的抗压弹性模量，A为主梁的横截面面积，L为主梁的长度。本文以碰撞有效刚度Keff为随机变量，其变异系数由混凝土弹性模量Ec决定，分布特征如表1所示。

2.4 不确定性分析区间

采用敏感性分析方法研究桥梁建模相关参数的不确定性对桥梁抗震性能的影响，以预测各参数在地震需求分析中的重要性。该方法实际上是基于单一变量法，即每次分析中只改变单个参数的取值，而其它参数均保持中值不变。因此，首先根据各参数的分布特征，确定前文提到的26个不确定性参数的上界、下界以及中值，分别对应5%,95%和50%的概率分位数，如表1所示。

3 地震波缩放

算例桥梁原型为某高速公路桥梁，设计基准期为100年，抗震设防类别为B类，工程场地为Ⅱ类，抗震设防标准：桥址处50年超越概率10%时的峰值地面加速度为0.2g, 地震反应谱特征周期为0.4 s。根据规范要求，需进行E1和E2两概率水平的抗震设计。本文选用FEMA-P695报告[24]中推荐的22对远场地震波作为地震动输入，这些地震波来源于自197-1999年期间全世界范围内发生的14次大地震实测记录，震级从M6.5～M7.6不等。FEMA-P695报告对这些地震波有详细介绍，本文不再赘述。

根据FEMA-P695报告的要求，使用这些地震波之前，首先要基于峰值地面速度(Peak Ground Velocity,PGV)对原始地震波进行标准化处理，以避免自来于震级、震中距、震源及场地类别等不确定性的影响，但仍然保留地震波之间固有的不确定性，使其适用范围更广泛。为适应我国抗震规范的要求，还需对这些地震波进行适当地缩放，根据FEMA-P695的缩放方法进行调整。既有的研究表明，在规则桥梁的地震需求分析中，结构基本周期对应的谱加速度(Spectral Acceleration,SA)比我国规范中的峰值地面加速度(Peak Ground Acceleration,PGA)更适合作为地震动参数。因此以算例桥梁第一阶振型周期对应的SA作为地震动参数。图2为E1和E2两种概率水平下地震波的缩放情况，由图可知，经过缩放处理以后的22组地波的谱加速度值与规范标准谱的加速度完全一致。需要说明的是，FEMA- P695推荐地震波实际上来源于PEER强震数据库，其中每组地震波均包含Fault Parallel和Fault Normal两个正交方向，考虑到每组地震波的频谱特性存在差异，其PGA，PGV和SA也不完全一致，因此，本文将每组地震波看作两条独立的地震波进行输入，即共有44条地震波用于分析。

图2 基于标准反应谱的地震波缩放(ξ=5%)Fig.2 Scaling of ground motions based on standard spectrum

4 建模不确定性敏感性分析

4.1 工程需求参数

既往的结构不确定性研究中往往只考虑了单个工程需求参数(Engineering Demand Parameter,EDP)的影响，例如，高层结构的层间转角(θ)或漂移比(%)。然而，桥梁工程在地震作用下可能存在多种破坏模式，因此，在桥梁地震需求分析中，需要同时考虑与这些失效模式相关的多个EDP的响应。此外，各种不确定性参数对不同EDP的影响是否一致仍有待研究。根据前文建立的桥梁有限元模型，本文主要考虑墩柱弯曲破坏、板式橡胶支座破坏、铅芯橡胶支座破坏、桥台破坏等几种破坏模式，因此，可确定工程需求参数如表2所示。

表2 工程需求参数表Tab.2 Engineering demand parameter

4.2 条带分析

本文采用条带分析法研究不同桥梁建模相关参数对结构地震响应预测的敏感性。首先，利用全部建模参数的中值(见表1)建立OpenSEES有限元分析模型，并分别输入E1和E2两种概率水平地震波，进行大量的非线性时程分析，实时记录表2中的8个EDP的最大响应值。由于地震动频谱特性的差异，相同SA作用下的地震响应一般是不同的。

条带分析中一般可采用对数正态分对结构的地震响应进行拟合[25]。本文采用极大似然法估计各构件的响应均值(μmi)和对数标准差(ζmi)。以中值有限元模型在E1和E2两种概率水平的地震波激励响应为例，图3给出了桥墩纵向响应(φL)、铅芯支座纵向响应(δLRB_L)、板式支座纵向响应(δPTEB_L)以及桥台被动响应(ΔAbut_pass)的条带法分析的结果。

图3所示的条带分析结果可为后文中的敏感性分析提供基础，即每次改变单个参数的取值，用表1中的下界值或上界值来替换中值，重复上述过程进行一系列的条带分析，可得到参数变化后的响应均值(μmi-,μmi+)和对数标准差(ζmi-,ζmi+)。需要指出的是，在改变单个参数取值的同时，其它参数均应该保持中值不变。

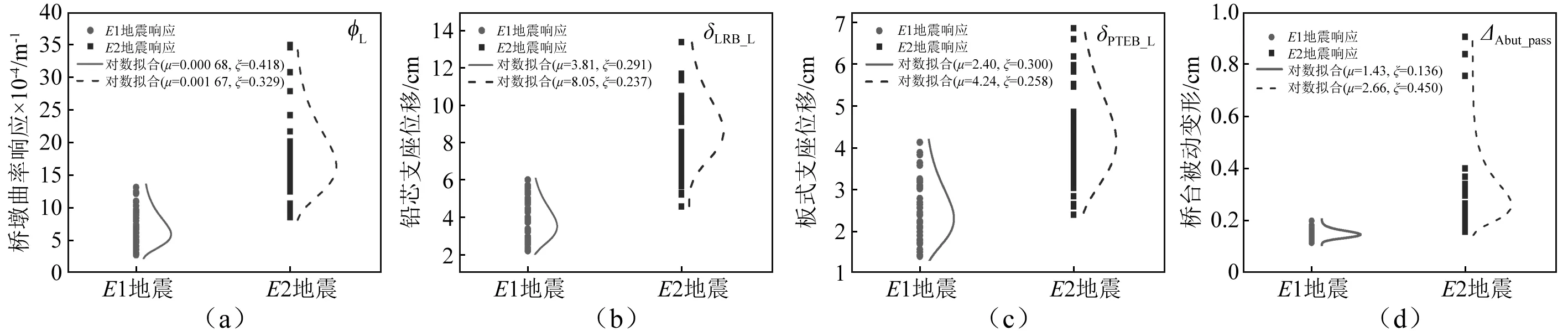
图3 不同工程需求参数基于中值模型的条带分析Fig.3 Stripe analysis of different EDPs based on the median bridge model

4.3 敏感性分析

基于以上条带法分析的结果，将桥梁各构件的响应均值和对数标准差在相同的概率分布区间的变化情况绘制在同一图中，并按变化量从大到小的顺序从上至下依次排列，可得到类似龙卷风形状的图形，即为敏感性分析中常用的龙卷风图。需要说明的是，一些地震波在缩放至E2概率水平时，会导致非线性分析出现不收敛的情况，这时可采用以下最大似然函数估计其对数正态概率分布的相关参数

(1)

式中：fX(x)为概率密度函数；FX(x)为累积分布函数；k为能使非线性计算收敛的地震波条数；n为条带分析用地震波的总数量。

图4为桥墩纵向响应在E1和E2概率水平地震作用下的响应均值和对数标准差的龙卷风图。如图所示，每个龙卷风图的中心纵轴对应所有桥梁建模相关参数均取中值的情况，则由中心纵轴向两侧伸出的柱状图长度可表示地震响应均值(μ)和对数标准差(ζ)对该参数的敏感性。柱状图越长意味着对应参数的敏感性越高。本文将桥梁建模相关的不确定性分为结构层次 (SU)、材料层次 (MU)以及边界条件 (BU) 三类。因此，与传统龙卷风图的统一排序法不同的是，本文将以上三类不确定性参数的影响用同一个龙卷风图来表示，但在图中又以虚线为界分为三层，对每一层都单独进行排序。图中，上层表示BU，中间层表示MU，下层表示SU。这样处理既可以纵向比较每类建模不确定性参数中影响最大的参数，还可以横向比较出不同类型不确定性参数间的影响大小。

值得指出的是，本文龙卷风图的排列顺序是根据建模相关参数对构件地震响应均值μ的影响大小排列的，而对数标准差ζ龙卷风图中的参数排列顺序则与均值龙卷风图的排列保持一致。由于篇幅限制，除图4外，本文只给出了桥墩横向φT、铅芯支座横向δLRB_T、板式支座纵向δPTEB_L和桥台被动方向ΔAbut_acti在E2地震作用下的龙卷风图，如图5～图8所示。

图4 E1和E2地震作用下φL的龙卷风图Fig.4 Tornado diagram of φL under E1 and E2 earthquake

图5 E2地震作用下φT的龙卷风图Fig.5 Tornado diagram of φT under E2 earthquake

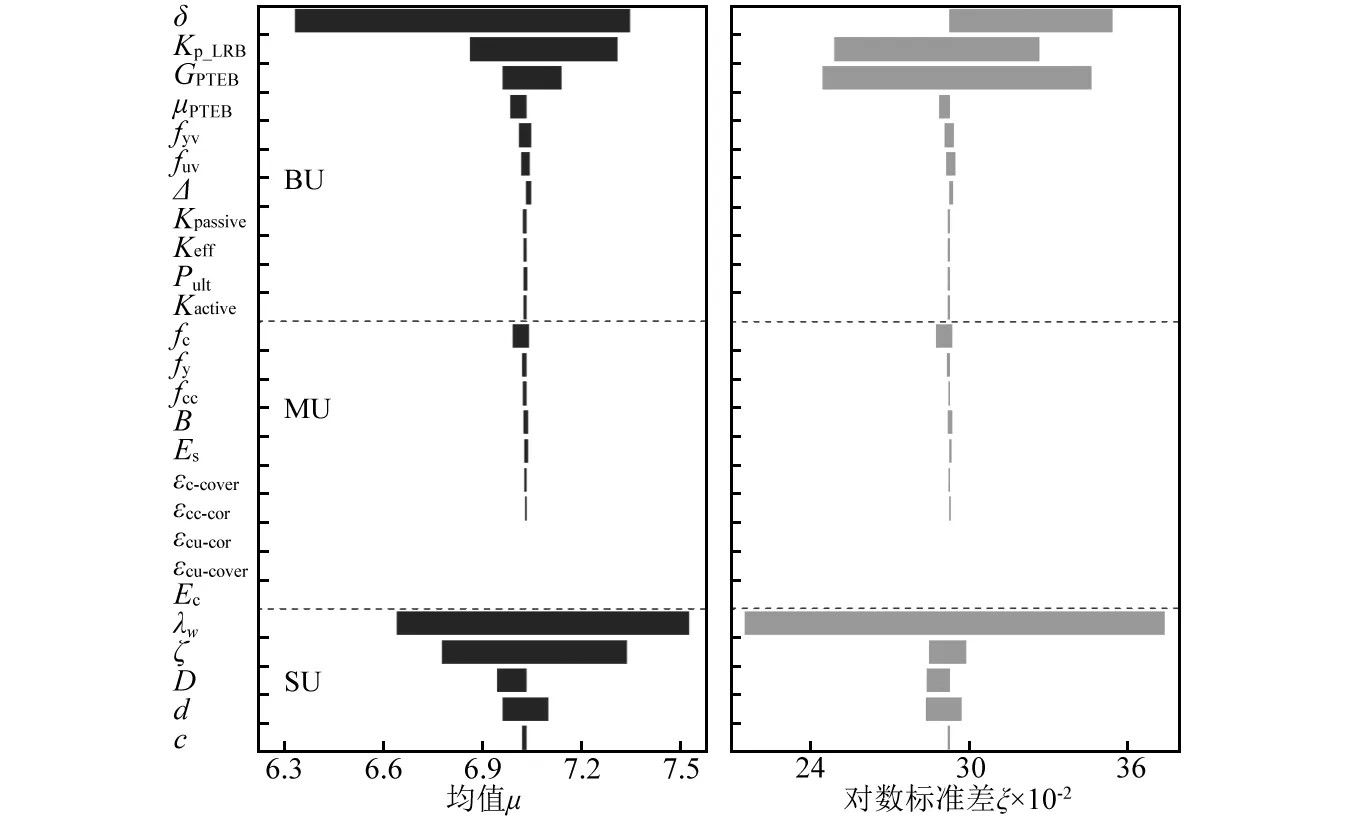
图6 E2地震作用下δLRB_T的龙卷风图Fig.6 Tornado diagram of δLRB_T under E2 earthquake

图7 E2地震作用下δPTEB_L的龙卷风图Fig.7 Tornado diagram of δPTEB_Lunder E2 earthquake

图8 E2地震作用下ΔAbut_acti的龙卷风图Fig.8 Tornado diagram of ΔAbut_actiunder E2 earthquake

4.4 分析结果讨论

由上一节的参数敏感性分析结果可知：

(1)随着地震激励强度的增加，影响桥梁结构地震响应预测的建模相关不确定性因素越多。如图4所示，在规范E1地震激励下，只有KP_LRB等6个BU参数和Es等5个MU参数对墩柱纵向地震响应(φL)预测有不同程度的影响，然而，在规范E2地震激励下，几乎全部的BU和MU参数都对φL预测有影响。这主要是由于在地震激励水平较低时，大多数构件仍能保持弹性状态，各种非线性特性并没表现出来。

(2)桥梁建模相关不确定性参数对构件响应均值μ和对数标准差ζ的影响并非完全相同。例如，由5可知，在规范E2地震激励下，对桥墩横向响应均值影响最大的结构层次不确定性(SU)是墩柱直径D，然而，对桥墩横向响应对数标准差影响最大的SU却是的容重系数λw。

(3)结构层次不确定性(SU)参数中的结构容重(λw)、阻尼比(ξ)和墩柱直径(D)对所有构件的地震响应预测都有较大的影响，但保护层厚度(c)以及纵筋直径(d)的影响则很小。

(4)由于本文只选取了桥墩的材料非线性参数进行分析，因此，材料层次不确定性(MU)仅对墩柱地震响应预测有一定的影响，但相比另外两类不确定性(SU和BU)的影响，MU对其它构件响应的影响非常小，特别是在规范E1地震激励下，对其它构件响应的影响几乎可以忽略不计。

(5)边界条件的不确定性(BU)参数的影响大小则因工程需求参数(EDP)的不同而不同。由图4～图8可知，尽管没有统一的规律可循，但仍可以归纳出三种情况：①具有方向性的参数。例如，伸缩缝间隙Δ对于纵桥向构件响应有一定的影响，但对横桥向地震响应几乎没有影响；横向挡块间隙δ则刚好相反，主要对横桥向的地震响应有较大影响；②与构件受力机制直接相关的参数，例如，桥台刚度参数(KPassive,KActive)对构件本身的影响明显大于对其它构件的影响；③对所有构件均有重要影响的参数。例如，铅芯橡胶支座和板式橡胶支座是桥梁上下部结构之间的主要传力构件，因此，KP_LRB,GPTEB和μPTEB对所有构件的响应均有较重要的影响。

综上所述，桥梁地震需求分析中有必要考虑各种建模相关不确定性的影响，但由于不同类型不确定性参数对结构地震响应的影响程度不同，在实际应用中可根据所建立的模型和研究对象的不同而选择只考虑一些重要的不确定性参数。根据本文选取的8个桥梁工程需求参数(EDP)的龙卷风图，可以分别对三类桥梁建模相关不确定性参数的重要性进行排序。对于每一类不确定性参数，如果假定龙卷风图中排前三出现次数较多的参数为重要的不确定性参数，则可总结出13个重要的桥梁建模相关不确定性参数，其中，SU参数3个、MU参数3个、BU参数7个，汇总如表3所示。需要指出的是，表中每一类重要不确定性的重要程度从左往右依次递减，即λw，fc和KP_LRB分别为最重要的SU,MU和BU参数。

表3 重要桥梁建模不确定性参数Tab.3 Important modeling uncertainty parameters

5 结 论

(1)桥梁结构的概率地震需求分析中，影响结构地震需求预测的建模相关不确定性因素随着地震动激励大小的增加而逐渐增多，这表明在进行强震作用下的桥梁倒塌性能分析时应尽可能多的考虑建模相关不确定性的影响。

(2)相比结构层次(SU)和边界条件(BU)的不确定性影响，材料层次(MU)的不确定性影响相对较小；SU对几乎所有的EDP都有较大影响，但BU的影响却因选取的EDP的不同而不同。因此，对不同桥梁构件进概率地震需求分析时，应合理的选择要考虑的不确定性因素。

(3)表3给出的13个重要不确定性参数对桥梁结构的地震需求影响较大，特别是即容重系数λw、混凝土峰值应力fc和铅芯支座的屈服后刚度KP_LRB的影响最大，在桥梁有限元建模时忽略这些不确定性，可能导致概率地震需求分析的结果不准确。

(4)单个不确定性参数对桥梁概率地震需求分析的绝对影响是有限的，大部分参数的影响甚至可以忽略，这主要是由于本文在生成龙卷风图时，每次只改变单个因素，忽略了多个因素之间可能存在的联动效应，在以后的研究有必要进一步研究建模不确定性参数间的相关性对桥梁地震需求的影响。