基于高斯多峰法的密闭空间爆炸特性曲线拟合
谢 威, 蒋新生, 徐建楠, 周 毅, 王 冬
(陆军勤务学院 油料系,重庆 401311)
在石油、化工安全防护中,研究易燃、易爆介质产生的爆炸超压等特性有着极其重要的意义。通过对其发展规律的研究探索,能有效地预测爆炸产生的危害,以便对爆炸防护装置的强度等参数进行设计、计算、分析。对于爆炸超压的预测和计算,国内外许多学者都已有较多研究,主要包括空气中爆炸超压[1-4]到密闭容器、有约束和无约束的泄压容器爆炸超压的预测计算研究[5]。由于受限空间爆炸的传播受距离、扰动、障碍物等的影响会加速,甚至可能形成爆轰,造成更大的破坏,引起了研究者们的重视[6]。而且,不同尺度的受限空间,其爆炸规律也不尽相同。所使用的研究手段主要有三种:①基于试验数据的信号处理[7-8];②基于爆炸理论的理论推导;③基于数值计算与爆炸理论相结合的数值模拟。
针对密闭空间或容器爆炸的研究,王淑兰等[9]对密闭容器内中心弱点火条件下的烃类气体的燃爆特性进行了计算研究;赵衡阳总结了密闭容器爆炸的三种简化模型:等温爆炸模型、绝热爆炸模型和一般模型,并将密闭容器气体或粉尘爆炸的理论和试验结果进行比较分析,验证了模型的可靠性;严清华等[10]利用数值模拟的手段,考虑流体动力学和化学反应动力学,对大型球型密闭容器内的可燃气体爆炸过程进行了数值模拟,弥补了解析解模型如等温爆炸模型不能对浓度、密度、温度等流场进行定量描述的缺点。但是,由于密闭容器爆炸的理论研究、数值模拟研究往往与实际环境、实际需求相差较大,得到的结论再投入工程应用的部分比较少,因此,利用试验数据结合理论分析来反推和修正理论数值进而投入应用,是有效解决问题的途径之一。
本文提出用高斯多峰拟合法对爆炸特性曲线进行拟合,利用多个高斯单峰函数的线性叠加趋近真实曲线,提高拟合精度,通过比较不同数量分峰时的残差分布,选择一个能较好反映原曲线总体特征的简化表达式,对进一步量化分析试验特性参量,如初始浓度、温度、压力等与爆炸的联系具有重要意义。
1 高斯多峰法应用于爆炸特性曲线拟合
高斯多峰法应用到信号波的处理上的研究比较广泛,比如Giorgos等[11]将其应用到波形激光雷达的信号处理上,Samjin等[12]将其应用于心脏频谱的分割,Gabriel等[13]将其应用于复杂色谱分析等等,而国内目前比较常见的应用领域是统计学与光谱分析[14-16],在其他领域的应用比较少见,但其本身却是很好的求曲线拟合的一种方法。而且高斯多峰的叠加性质可以很好契合爆炸过程中各种爆炸波(泛指爆炸过程中所有具有可叠加性质、震荡特性的爆炸表征),比如,压力波、速度波、火焰波、声波等等的叠加,尤其是在密闭空间中,由于容器等约束的限制,引起爆炸压力波的径向传播受阻,而轴向传播得到加速,后产生的爆炸压力波追上之前的爆炸压力波,不断叠加,在前方产生更强的叠加压缩波,当传播距离足够长时,最终将形成爆轰波。
在爆炸特征参量-时间(f-t)曲线上,可以将高斯单峰函数看作某一波动的波动能量随时间的变化过程,多个单峰曲线的叠加,就等于同一时刻不同波动能量的叠加,意味着某一测点某一时刻受多个波动的影响。而在爆炸特征参量-距离(f-x)曲线上,可以将高斯单峰函数看作某时刻某一波动的波动能量随位置的变化过程,多个单峰曲线的叠加,就等于同一位置不同波动能量的叠加,也意味着某一时刻某一位置受多个波的影响。此外,爆炸过程总伴随着振动频率先不断增大后逐渐降低的压力波振荡现象,如需更精确的描述爆炸特性曲线,可以对曲线进行修正
f(t)=M(t)+Di(t)+Fi(t)(i=1,2,3,4,...,n)
(1)
式中:f(t)为修正值;M(t)为拟合值;Di(t)为修正爆炸波高频区间的振动函数;Fi(t)为修正低频区间的脉动函数,且Fi(t)的脉动变化是先增强后慢慢变弱,利用频谱图分析高频和低频段的频率和振幅,找到对应的函数。
2 高斯多峰拟合法
高斯单峰的函数表达式为
(2)
式中:y0为函数的基准值;W为控制峰宽的峰宽函数;A为高斯函数的面积函数,可正可负;Xc为高斯函数的峰轴。
标准的高斯函数曲线就是正态分布曲线,其基值为0,中心轴为x轴,积分面积恒为1,如图1所示。

图1 标准的高斯函数曲线Fig.1 Standard Gaussian function curve
高斯多峰拟合法就是利用高斯单峰函数在不同位置的叠加来拟合出需要的近似曲线,并得到一个函数表达式。高斯多峰的函数表达式为
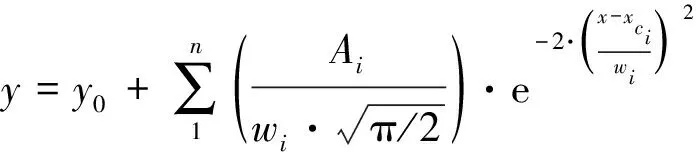
(3)
当y0=0时,记
(4)
则有
(5)
(6)
也就是说原函数的积分等于分峰后的所有单峰面积求和。
3 密闭容器爆炸试验
试验主体为φ700×3 000 mm,耐压10 MPa的长密闭圆管,点火位置都在图2左侧法兰中心,压力测点位于末端中心,可燃气体为汽油蒸汽,采用真空泵循环,如图2所示。辅助设备包括:WGDH-5型高能点火器;TST6300压力数据采集系统;GXH-1050碳氢分析仪——用于测定试验系统初始状态时内部的可燃气体体积分数。为保证预混均匀,在停止充气后,需继续循环一段时间然后静置10 min。若各测量点碳氢分析仪的读数变动在0.3%范围内,即说明试验容器中的可燃气体混合均匀。试验共进行5次,以保证试验的可重复性,并从所得的数据中选取具有代表性而且振动特性比较明显的一次试验数据作为试验结果。
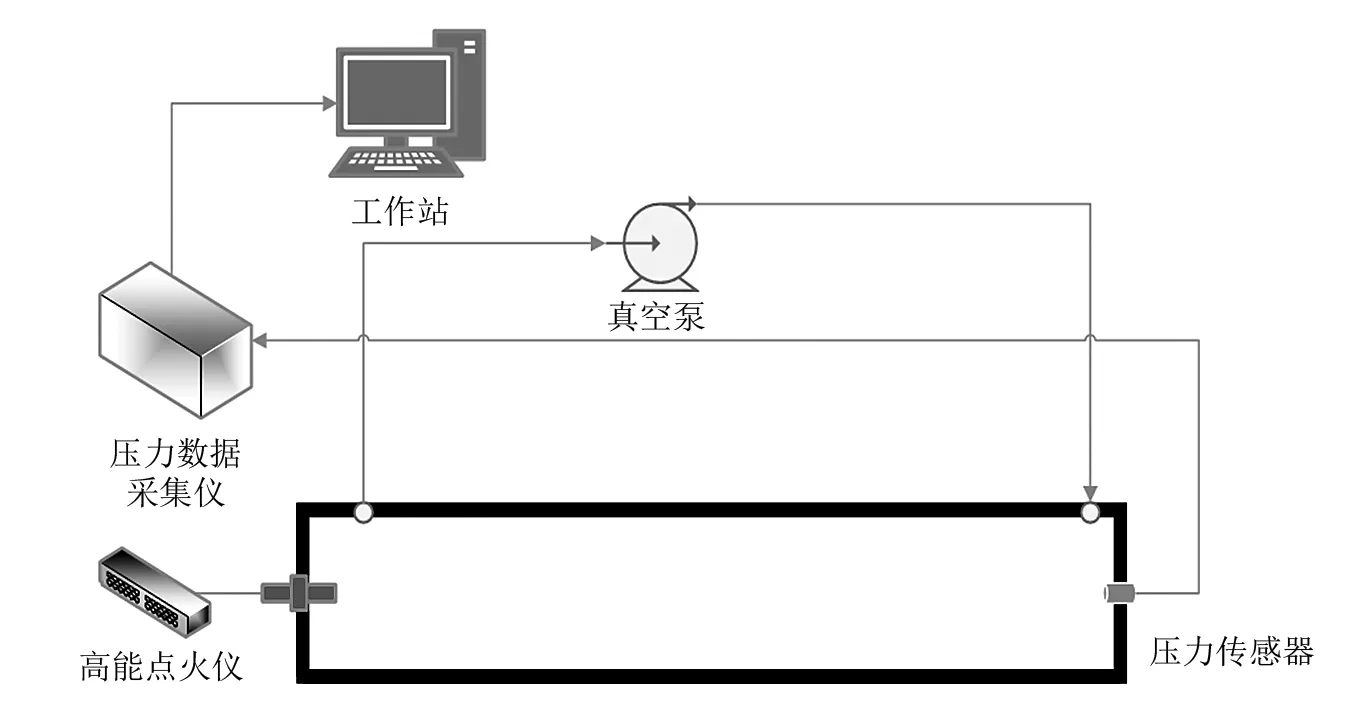
图2 试验布置示意图Fig.2 Experiment layout diagram
测得的密闭空间内末端的油气爆炸典型压力-时间曲线,如图3所示。由于密闭容器爆炸产生的压力振荡前期得到不断加强,当振动频率足够大时,会引发容器振动和传感器干扰,使得试验采集到的数据存在一定的干扰误差。所以,在进行数据拟合前,可以先利用傅里叶变换进行适当的滤波预处理,使曲线便于拟合计算,如图4所示。

图3 可燃气体爆炸试验实测p-t曲线Fig.3 Measured p-t curve of combustible gas explosion

图4 实测数据滤波后的p-t曲线Fig.4 Data curve of p-t after filtering
由于拟合所采用的数据是基于瞬态压力数据采集系统采集到的压力数据,而且传感器为压阻式,因而可视其为一维压力波动数据,方向为垂直于传感器方向,所以采用高斯多峰法对该压力-时间曲线的拟合,仅是对该点的压力波在一维尺度上的近似分析。
4 密闭空间爆炸压力特性曲线拟合及结果分析
将高斯多峰函数法具体应用到爆炸压力特性曲线p-t上,对比油气体积分数为2.0%(其爆炸极限为1.4%~7.6%)时管道爆炸试验测得的曲线图与不同峰数拟合得到的曲线图。具体的操作步骤,如图5所示。先对试验曲线进行滤波处理,滤掉高频的一些干扰和振动,得到一条相对光滑的曲线(见图4)。然后,利用Origin软件对曲线进行峰分析和以高斯函数为基函数的多峰曲线拟合[17]。分析滤波后的曲线,取一较小峰数(n=6)对曲线拟合,得到的图形如图6所示。但是,由于Origin软件目前的最大迭代步数限制为400步,若能继续迭代,将得到更适合的表达形式。
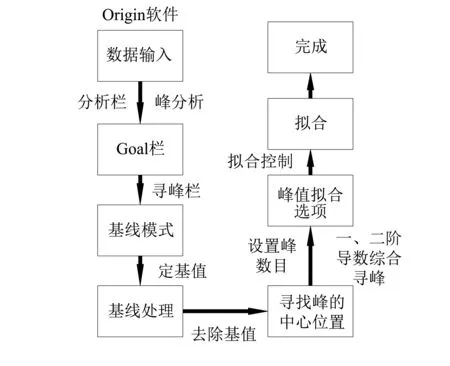
图5 详细操作步骤Fig.5 Operation details
通过拟合可以看出,分峰数为6时,拟合的曲线基本可以体现出爆炸压力发展的整体过程,其拟合的确定数COD(R2),也就是校正后的相关系数平方为0.995 17,如图6所示。由图6可知,利用高斯多峰拟合法对爆炸压力曲线进行分析时,将所得Fit Peak按照峰中心出现时间及幅值进行排序,可得到两类峰:一类是构成超压曲线主体,称为主体峰,其表征了整个超压曲线的总体变化趋势;另一类是构成超压曲线出现最大值时的振荡峰,称为特征峰,其表征了超压振荡的压力波动细节,幅值、峰宽一般都较小。对于分峰数为6时的拟合曲线来说,峰1、峰3、峰4、峰5、峰6为主体峰,峰2为特征峰。可见超压最大时的压力波动细节体现明显不足,其残差波动也比较大,因此只能满足对爆炸超压总体趋势的估计,其相关参数,如表1所示。

图6 分峰数为6的拟合情况Fig.6 The case of six fit peaks

表1 拟合曲线的相关参数Tab.1 Parameters of the fitting curve
实际上,6个高斯函数拟合后的曲线是对原压力曲线的比较粗糙地光滑,为了更逼近原始曲线,尝试采用采用12个高斯函数叠加来对其进行拟合,得到的结果,如图7所示。
通过拟合可以看出,分峰数为12时,拟合的曲线更加接近爆炸压力发展过程,其拟合的确定数COD(R)为0.998 46。其中峰1、峰2、峰5、峰6、峰8、峰9、峰10、峰11、峰12为主体峰,峰3、峰4、峰7为特征峰。随着主体峰数量的增加,压力的整体变化趋势愈加精确。而特征峰增加不明显,虽然超压最大时的压力波动细节比6峰时要好,残差波动也比6峰时小,但是压力波动细节的体现仍然略显不足。其相关参数如表2所示。
为了更加体现压力波动细节,达到增加特征峰的目的,在超压曲线达到最大值时多选取几个分峰点,并采用20个高斯函数对其进行拟合,得到的结果如图8所示。
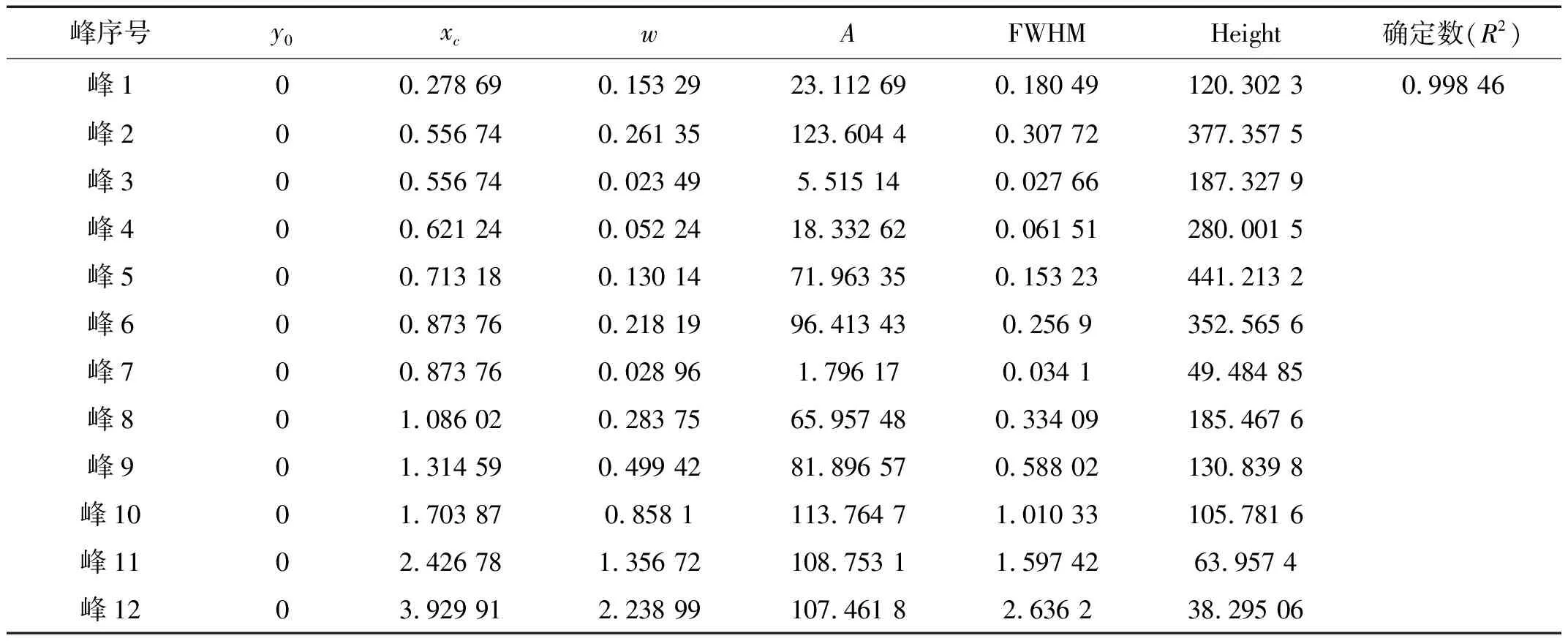
表2 拟合曲线的相关参数Tab.2 Parameters of the fitting curve
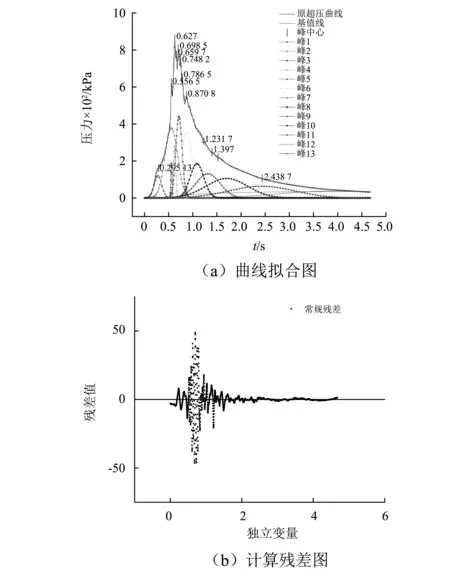
图7 分峰数为12的拟合情况Fig.7 The case of twelve fit peaks

图8 分峰数为20的拟合情况Fig.8 The case of twenty fit peaks

表3 拟合曲线的相关参数Tab.3 Parameters of the fitting curve
分峰数为20时,拟合的曲线几乎与原爆炸压力曲线没有多少区别,其拟合的确定数COD(R2)为0.999 4,得到的拟合曲线表达式为
式中:Fit Peak3在该拟合段的值都为0,可以忽略,峰1、峰2、峰3、峰4、峰12、峰14、峰15、峰17、峰18、峰19、峰20为主体峰,峰5~峰11、峰13、峰16为特征峰,因此其压力波动细节明显比12峰时更好,残差波动也比12峰时小。但遗憾的是,由于Origin软件迭代步数的限制,使得结果仍不能完全达到预期效果,出现了负向波动的情况。若能继续迭代的话,可得到更加精确的结果,将原曲线精确得划分为主体峰与特征峰。拟合曲线的相关参数,如表3所示。
4.1 分峰数量与拟合效果的关系
通过拟合结果可以看出,最终拟合曲线与寻峰的峰轴位置及数目相关;在满足迭代步数足够多的前提下,随着分峰数目的增加,拟合曲线的残差值的范围会缩小,拟合精度会越高,分出来的主体峰与特征峰会更加精确。当峰的数量较多时,高斯单峰之间的间距越少,其主体峰的拟合方式越接近连续变换,其峰值、峰轴、峰宽也可进行二次拟合得到面积函数A(t)、峰宽函数w(t)、峰轴函数Xc(t)。也就是说,只要高斯单峰的基数量n足够多,则拟合出来的曲线可以无限接近试验测得的爆炸特性曲线,其表达式可以写成
(7)
式中:pi(t)为特征峰函数;Pz(t)为主体峰复拟合函数,其积分的具体表达式为
(8)
但是,通过试验发现,随着分峰数的增加,相邻峰轴越来越接近,其产生负向峰的数量也会增加,拟合的成功率会降低,所需要的计算时间及迭代步数会大大增加,拟合的优化效果变化越来越不明显,越难得到一个理想的拟合结果。因此,我们只需要在满足精确度的前提下,找到一个合理的峰数即可。
4.2 分峰参数与爆炸压力变化过程的对应关系
高斯单峰函数本身的几个参数都具有显著的几何含义,其中,峰的高度Height计算为
(9)
(10)
半峰宽的计算为
(11)
峰的高度在压力-时间曲线上表示的含义是单峰的最大超压值;半峰宽的大小则与单峰的升压速率相关,同时也表征了拟合峰的作用时间。
如图9所示,以6个高斯函数拟合为例,采用高斯函数对爆炸压力-时间曲线进行拟合,就是对爆炸模型的简化,将爆炸的整个过程看作是多个不同时刻的不同幅度的单个压力脉冲的叠加。也就是说,采用脉冲叠加的方式可以模拟出接近实际爆炸的超压等效过程。

图9 6高斯函数拟合的三维图Fig.9 The three-dimensional curves of the case of six Gaussian peaks
4.3 单峰积分与爆炸冲量的关系
对每一个高斯函数进行积分,可以得到高斯峰面积。由于基线从0时刻开始,小于0时刻的积分几乎可以忽略不计,因此高斯峰总面积可以近似表示为
(12)
也就是说,爆炸产生的超压总冲量近似等于单个峰的超压冲量之和,而高斯函数的积分是比较容易求得的
(13)
因此,利用高斯多峰拟合法可以非常快速的求出单峰的超压冲量,进而估计出整个爆炸的总冲量。
5 结 论
为了更加细致、量化地研究可燃气体爆炸超压振动的主要特性,本文从试验的角度出发,采用高斯多峰拟合法对试验所得的爆炸超压曲线进行了分析,得到如下结论:
(1)拟合结果的精确度与寻峰的峰轴位置及数目相关。当用12个高斯函数去拟合时,拟合曲线的主体变化趋势比6个高斯函数拟合时更精确;当增加超压曲线达到最大值时的分峰数时,拟合曲线的波动细节体现更明显,其精确度高达99.94%。
(2)高斯多峰拟合法能得到比较精确的密闭空间爆炸超压函数表达式,其对密闭空间爆炸超压的预测及规律研究具有重要意义。
(3)高斯多峰拟合能得到爆炸超压波动的等效模型,采用多个不同时刻不同幅值的脉冲叠加,可以等效实际爆炸的超压过程。
(4)高斯多峰拟合法得到的单峰的面积积分之和就是整个爆炸超压的冲量大小,采用此方法能快速地估计出整个爆炸超压的总冲量。
在实际应用时,应根据实际需要适当调整计算时间及迭代步数等参数,提高拟合效率。

