带状结构的高斯图模型嵌套惩罚估计

李凡群，张新生

（1.安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030；2.复旦大学 管理学院，上海 200433）

0 引言

无向图可以用G=(V，E)来描述，其中V包含p维随机变量X=(X1，…，Xp)的p个顶点（node），边集(edge)E={eij|1≤i＜j≤p} 描述了X=(X1，…，Xp)这p个顶点之间的两两条件相依性。当且仅当Xi和Xj在给定其他变量时是条件独立的，则称Xi和Xj之间不存在边，即E中不存在元素eij。如果X=(X1，…，Xp)服从高斯分布N(μ，Σ)，则记 Ω=Σ-1为协方差矩阵的逆矩阵，称为精确矩阵。在高斯分布场合的图模型中，Xi和Xj之间不存在边等价于给定其余变量的条件下，Xi和Xj是条件独立的，这又等价于Ω中元素ωij=0。于是高斯图模型的恢复和参数估计问题就等价于其协方差矩阵或其精确矩阵的估计以及精确矩阵中的零元素的识别问题。

Lauritzer[1]介绍了高斯图模型的性质，并把图模型选择和估计的方法应用于高斯图模型。Meinshausen和Bulmann[2]提出相邻点选择的方法。Levina等和Fredman等[3,4]把惩罚似然的方法用于精确矩阵的估计及图模型的恢复。Fan和Peng[5]用自适应Lasso和SCAD惩罚选择图模型和参数估计。Zhang等(2014)[6]提出D-trace损失，在约束条件下，通过最小化D-trace损失，获得了稀疏的精确矩阵的估计。

尤其是多维随机变量有序的，比如纵向数据、时间序列、空间数据及光谱数据等。该类数据的特点是顶点间的条件相依性与顶点之间的位置有关，位置越远，条件相依性越弱，称该类模型为带状结构高斯图模型。对这类数据，Smith和 Kohn[7]，Huang等[8]提出对正定矩阵做修正的Cholesky分解：Ω=(1-Φ)TD-2(1-Φ)，其中Φ是主对角线上的元素为1的下三角矩阵。D为对角形矩阵。Bickel等(2008)[9]通过对协方差矩阵的元素设置门限以确定带宽，Levina等(2008)[3]对修正的Cholesky分解因子Φ提出嵌套的Lasso估计。Cai等(2011)[10]提出l1惩罚CLME方法，通过解线性规划，获得协方差矩阵的估计。本文利用精确矩阵的诸列(行)元素的系列线性回归模型的解释，对系列回归模型的回归系数施加嵌套的惩罚，得到精确矩阵的估计。与有关文献相比，该方法更能直接获得估计结果。随机模拟结果表明，对精确矩阵施加嵌套的惩罚的估计提高了估计的精度。

1 精确矩阵的诸列元素的系列线性回归模型的解释

令X=(X1，…，Xp)T为一个p维随机变量，且X～N(μ，Σ)。为了表达方便，本文用Σi，j表示移去Σ的第i行和第j列的的子矩阵，Σi，j表示Σ的第i行，其中第j个元素被移去，Xi表示移去变量X的第i个变量后的p-1维的随机向量。如果对X，μ，Σ做如下分块：

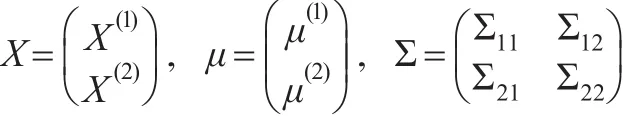
则由多元统计知，在给定X(2)=x(2)的条件分布为[11]：

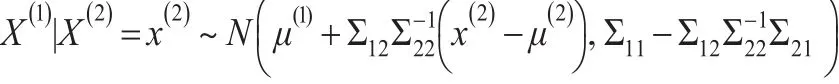
特别地，取X(1)=Xi，X(2)=Xi

那么在给定其余变量Xi=xi的条件下，Xi的条件分布为：

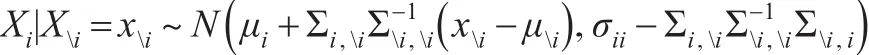
如果把Xi看成响应变量，其余变量Xi看成协变量，考虑如下的线性回归模型：

此时令β(j)=(β1，…，βj-1，βj+1…，βn)T，ϵi与Xi相互独立，并且在均方意义下：

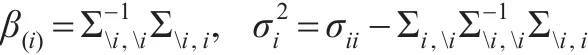
另一方面，若令Ω为多元正态分布X～N(μ，Σ)的精确矩阵，则由ΣΩ=I，有：

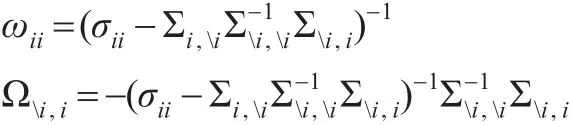
对每一个i(i=1，2，...，p)，得到精确矩阵Ω的诸对角线上的元素ωii以及其第i列上其余元素Ωi，i与回归问题（1）中回归系数β(j)及残差方差之间有如下关系：

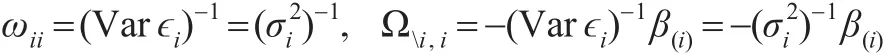
这表明精确矩阵Ω的第i列的元素Ωi，i与回归系数成比例，于是Ωi，i中的零元素与β(j)中的零元素相对应，反之亦然。从而高斯图模型的参数估计与模型选择可以转化为对回归问题（1）的模型选择及对残差的方差的估计。基于估计

2 精确矩阵嵌套的l1惩罚估计

2.1 嵌套惩罚函数

根据前文的分析知，精确矩阵Ω中每行元素有相应的回归问题中回归系数的解释。并且模型恢复与参数估计的问题转化为对回归系数β(j)和残差方差的选择和估计问题。

基于模型（1）的β(j)和的负的对数似然函数为：

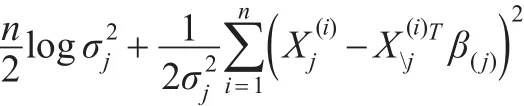
(j)惩罚似然的估计为：

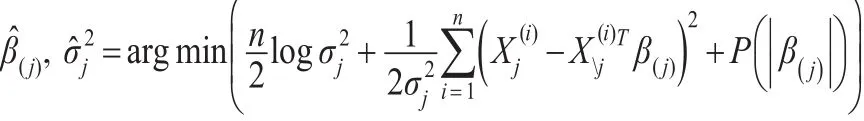
Levina等(2008)[3]基于改进的Cholesky分解，对cholsesky分解因子每行元素提出嵌套的惩罚，得到嵌套的分解因子估计。

下面本文基于带状模型对应的回归模型，对其系数β(j))提出如下的嵌套惩罚函数：

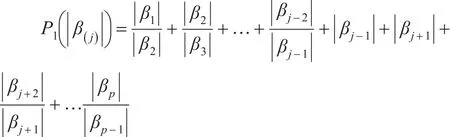
该惩罚函数相当于加权的l1惩罚函数。在该惩罚下，一方面，当 k＜ j 时，若0。这意味着精确矩阵Ω的第j行元素有估计当l＞j时，若这意味着精确矩阵Ω的第j行元素有估计于是通过该惩罚，得到的图模型估计保证了其带状结构特性。

考虑到 |βj-1|，|βj+1|的分母为1，故对 |βj-1|，|βj+1|两个参数的惩罚在尺度上和其余参数不一致，所以对P1(|β(j)|)做如下两种改进：

2.2 局部平方近似以及牛顿迭代算法

本文利用迭代算法，通过最小化：

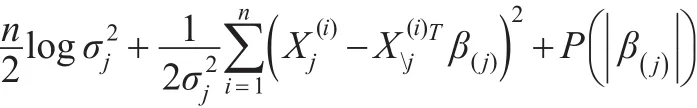
得到β(j)和估计。

第一步：给定β(j)的当前估计值,计算：

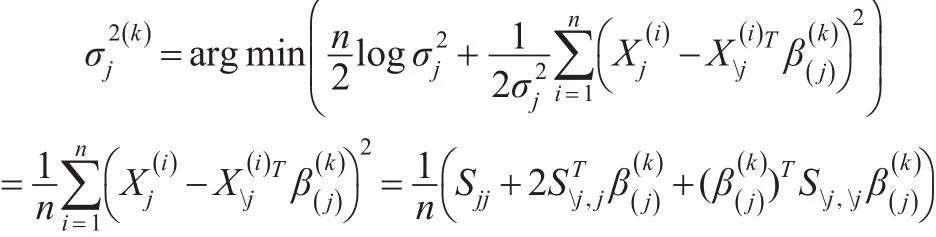
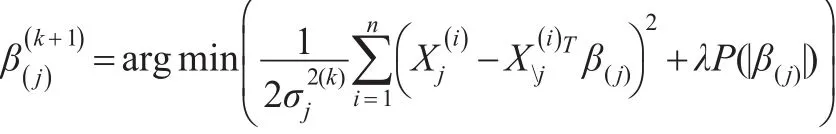
对每一个j=1，2，…，p重复以上两步，直到满足一定的准则，从而得到诸β(j)和的估计，根据前文的分析，得到精确矩阵的估计。由于函数不是关于β(j)的凸函数，为了克服计算上的困难，本文对诸进行局部平方近似，得到了的显式表达式。

一方面，对于惩罚函数的分子部分，令：

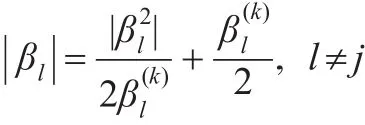
则上述三个惩罚函数经过局部平方近后得到如下形式：

其中C1为常数为对角形矩阵:

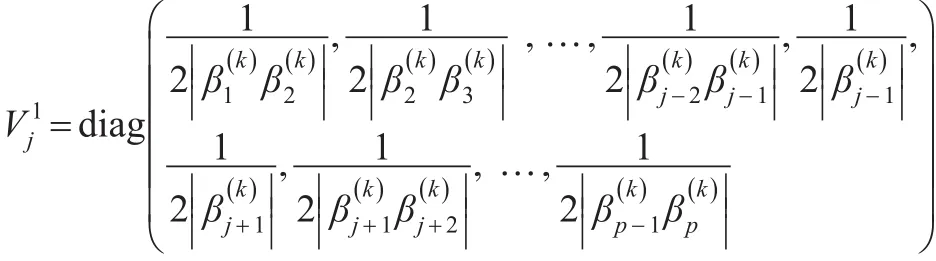
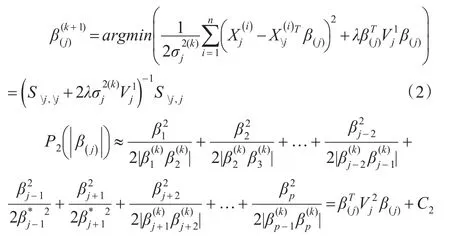
其中C2为常数，为对角形矩阵:

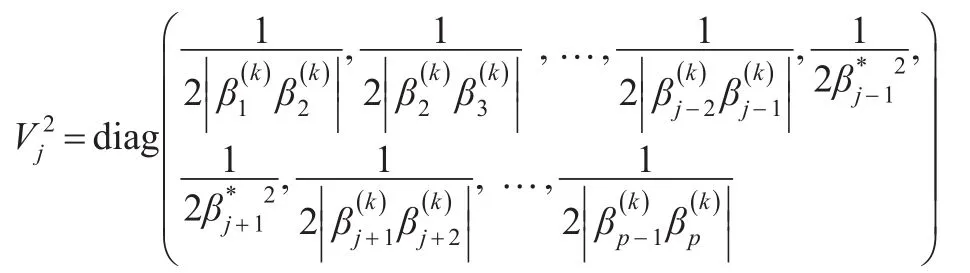
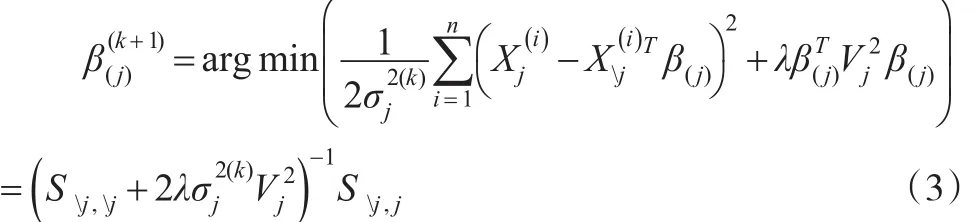
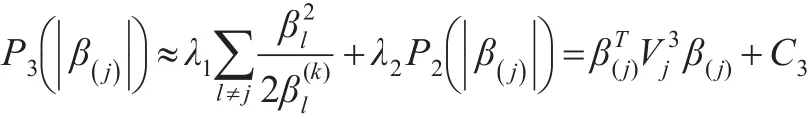
其中C3为常数，为对角形矩阵:

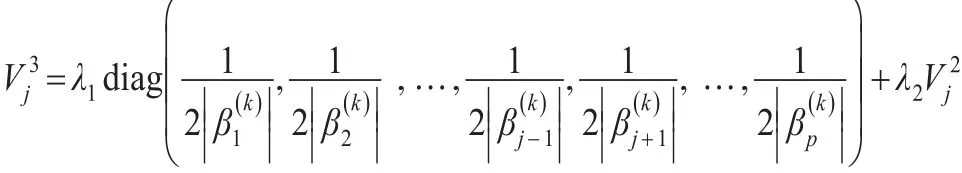
3 随机模拟

下面通过几个例子，分别计算估计的损失，比较不同方法的估计的精度。本文用K-L损失来度量估计的精度：把本文的方法得到的估计Modified nested Lasso简记为MNL，并把结果同以下方法的估计进行比较，包括基于Cholesky分解的nested-Lasso(CNL)[3]，g-Lasso[4]，以及由经验协方差矩阵得到的精确矩阵的估计记为Sample。考虑p=30，50，100，200的情况，对于每一个例子中的每一个p，从真实的模型中产生50组样本数据，每组样本数据各包含200个观测值。分别利用BIC和CV准则，选取调节参数λ。

在进行迭代过程中，当参数的估计的绝对值|βk|＜10-5时，令 |βk|=0。由于模型1是稀疏的，所以本文报告了BIC准则和CV准则下的估计结果。对于每一个模型，由式（2）至式（4），本文分别计算了三种迭代估计的结果，列出其中估计的最小损失以及损失标准差。所有结果列于表1和表2所示。表1和表2表明，基于精确矩阵元素的回归模型的改进的嵌套惩罚估计一致优于所列的其他方法。

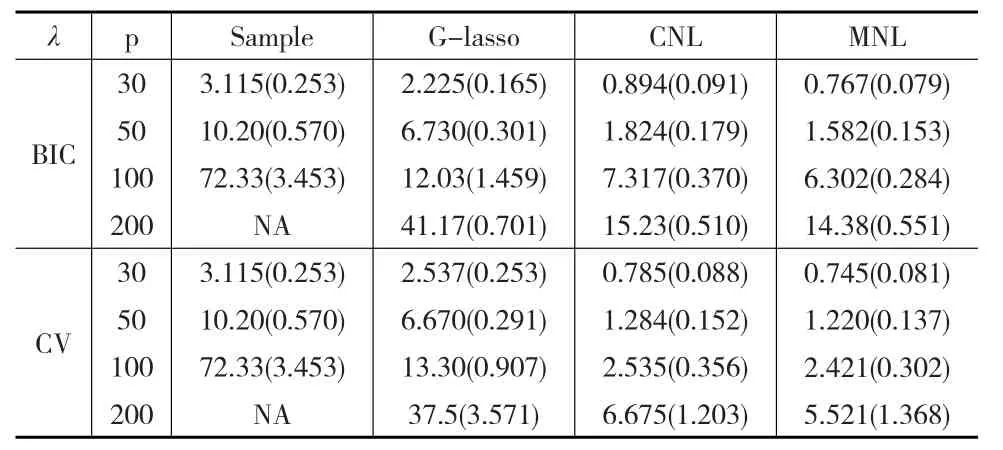
表1 K-L损失下不同的估计方法对模型1的估计结果

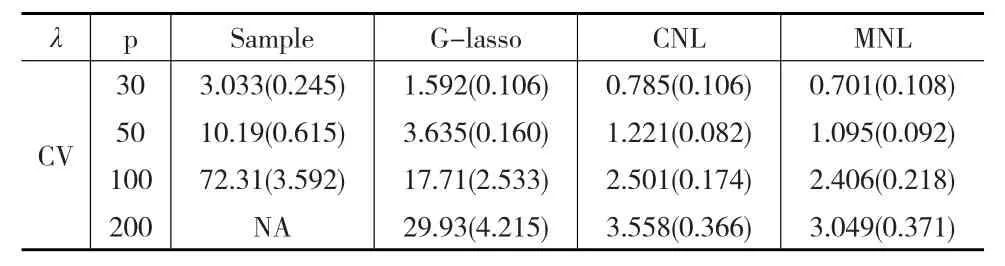
表2 K-L 损失下不同的估计方法对模型2 的估计结果

（1）模型1(AR(3))：精确矩阵Ω=(ωij),其中ωij=0.5|i-j|，|i-j|≤3，i≠j,以及ωii=1,其他场合ωij=0。

（2）模型2（完全模型）：精确矩阵 Ω=(ωij),其中ωij=0.5|i-j|。

4 结束语

本文在具有带状结构的高斯图模型场合下，利用高斯图模型的精确矩阵的诸元素可以利用系列线性回归模型进行解释的性质，对诸线性回归系数施加嵌套的l1惩罚，得到精确矩阵的改进的嵌套Lasso估计。通过局部平方近似及牛顿迭代算法，能很方便得到估计结果。与基于改进的Cholesky分解的嵌套Lasso估计相比，本文的方法能更直接得到精确矩阵的估计，减少了估计损失。数值模拟结果表明精确矩阵的嵌套Lasso估计提高了估计速度和估计精度。