基于全人口死亡率数据的随机死亡率模型拟合效果比较

樊 毅，张 宁

（1.中南林业科技大学 经济学院，长沙 410004；2.湖南大学 金融与统计学院，长沙 410006）

0 引言

近些年来，死亡率的持续下降带来的平均预期寿命的提高成为了世界各国人口发展的重要特征，我国也不例外。根据国家统计局发布的数据，我国人口的人均预期寿命已经从建国初期的40岁左右增加到了2015年的76.34岁。人的预期寿命的不确定性也会因人们在生活方式上的变化、医疗技术上的创新等因素而增加。预期寿命变动的随机性不利于养老金成本的核算，并在很大程度上影响到各种养老金计划的可持续发展，从而很可能会对寿险公司和养老金机构造成损失。综上所述，在与历史数据进行比较的基础上，选择与我国人口死亡率分布状况拟合效果较好的随机死亡率模型，可以使得死亡率预测的精准性得以大大改善，这为我国寿险企业和养老金机构的实践提供了理论支持。

近二十年来，国内外学者对随机死亡率模型进行了一系列的研究。其中随机死亡率模型同时考虑了年龄因素和时间因素对死亡率的影响，使得其预测值更接近实际。目前为止，由Lee和Carter(1992)[1]提出的Lee-Carter（LC）系模型和由Cairns等(2006)[2]提出的CBD系模型是较为经典且运用广泛的模型。

国内学者虽然有利用死亡率模型对中国人口死亡率进行预测，但是将不同死亡率模型对中国人口的拟合效果进行比较分析的研究相对较少。王晓军和蔡正高（2008）[3]在全面综述了各类死亡率模型的基础上，为中国的死亡率模型选择提供了合理建议。王晓军和黄顺林（2011）[4]比较分析了几个较为常用的随机死亡率模型对我国男性人口死亡率历史数据的拟合效果，发现在CBD模型基础上拓展而来的一个模型对中国男性人口死亡率经验数据的拟合效果最好。段白鸽和石磊(2015)[5]在动态死亡率模型的构建中考虑了超高龄人口死亡率的因素，建立了超高龄人口动态死亡率分层模型，分析了我国人口死亡率的变化状况和该模型预测的效果。张志强和杨帆（2017）[6]首次在人口死亡率预测中运用了多变点检测方法，其将Lee-Carter模型与在主成分分析基础上建立的死亡率模型对多个国家数据进行拟合，发现采用多变点检测的基于主成分分析的死亡率模型对人口死亡率预测的精确度和稳定性更优。

本文在全面综述各类死亡率模型的基础上，选择了8个运用较为广泛的随机死亡率模型，以此对中国1994—2013年总人口死亡率的经验数据（0～89岁）进行比较分析，并在综合考虑拟合效果的基础上作出评价，以此得出最优模型。

1 随机死亡率模型

死亡率模型主要划分为确定型和随机型两种。其中确定型死亡率模型不考虑时间因素和死亡率未来趋势对其造成的影响，只假设死亡率与年龄相关，且该种模型的参数由死亡率的经验数据确定。目前，随机死亡率模型可划分为LC系和CBD系死亡率模型。

1.1 Lee-Carter模型

在有关随机死亡率的研究中，比较著名的是由Lee和Carter于1992年提出的Lee-Carter模型：

其中，αx，βx指年龄因素，kt指随机时间因素。m(x，t)指在t时刻年龄为x岁的人的中心死亡率，αx指不同年龄段死亡率对数变动的基数；βx指不同年龄段死亡率对数变动的趋势。kx指时间因素变量，可当作一个随机游走过程或一个ARIMA过程，表示在t时刻死亡率的变动情况。

如今进行参数估计的方法有许多。Lee和Carter（1992）[1]提出的SVD法 (Singular Value Decomposition)是最早进行参数估计的方法。之后，统计方法更加标准化，注重对全部数据的拟合程度[7,8]。但 Lee和 Miller（2001）[9]认为，应更加注重对数据集最后一年的拟合，因为最后一年的数据对未来死亡率预测的影响要大于其他年份数据。

1.2 包含出生年效应的Lee-Carter模型

2006年，Renshaw和Haberman[10]第一次将出生年效应纳入人口死亡率模型：

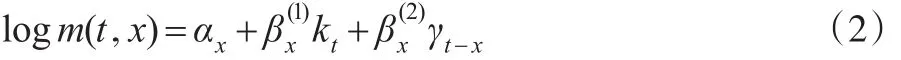
其中，kt指随机时间因素，γt-x指随机的出生年效应，是（近似）出生年份(t-x)的函数。Renshaw和Haberman（2006）[10]将英格兰和威尔士的数据进行分析后，发现相较之前的Lee-Carter模型，加入出生年效应会使人口死亡率模型更加完善，但该模型（RH模型）的稳定性不佳。CMI(2006)[11]发现模型的参数估计值会随着死亡率数据的年龄范围变化而变化；Cairns等(2008)[12]用不同时间范围去拟合模型的过程中也意识到了这个缺陷，他们还进一步意识到用该模型拟合的出生年效应大致存在一个确定的线性趋势或二次趋势，这或许会对模型的拟合效果造成影响。

Haberman和Renshaw（2011）[13]令RH模型中的=1以解决其稳定性问题，具体简化形式如下：

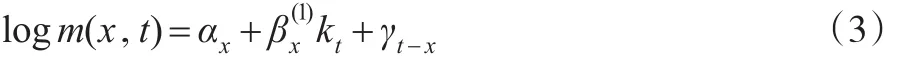
Currie等(2006)[14]在简化了RH模型后，建立了APC模型：

该模型能够很好地拟合美国的历史数据，也能解决RH模型在上文中提到的稳定性问题[11]。

1.3 CBD模型及它的拓展模型

针对高龄人群，Cairns等(2006)[2]提出了一个基于Logistic转换的CBD模型：

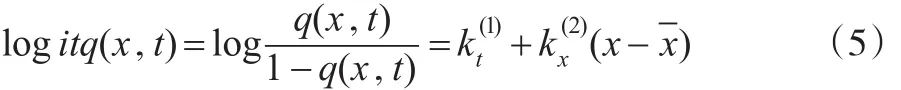
其中，q(x，t)=1-exp(-m(x，t))，指在t年内x岁的人死亡的概率，-x为样本年龄均值，为具有漂移项的双变量随机游走kt=kt-1+μ+cZt，因此该模型也被称为双因素死亡率模型。此外，他们在分析中还详细说明了如何利用贝叶斯方法在模拟中包含参数的不确定性。

之后，Cairns等(2007)[15]进一步拓展了CBD双因素模型：

Cairns等(2008)[12]将原始模型进一步简化，建立了两个模型，一个模型是令=0，见公式（7）；另一个模型是令是零，用更复杂的年龄-出生年效应因子替换，见公式（8）：

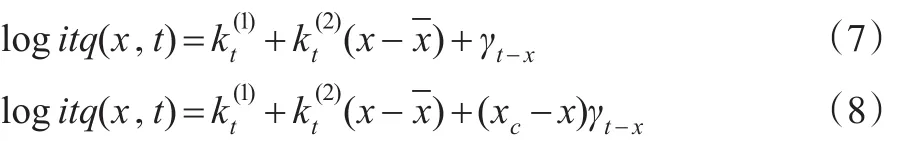
1.4 Plat模型

Plat(2009)[16]在审查和分析LC系和CBD系等死亡率模型后，建立了四因素死亡率预测模型：

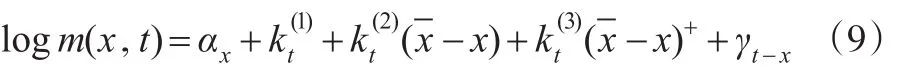
其中，αx与Lee-Carter模型中的类似；代表各年龄死亡率随时间的变化程度；指各年龄段的人死亡率改善水平的差别；是指由于滥用药物、暴力或酗酒等原因而使低龄人群的死亡率出现波动，此处用(-x)+=max(-x，0)来代替-x)，目的是使死亡率-年龄曲线变动趋势与以往数据相吻合。若仅仅预测高年龄组人群死亡率，可剔除，使模型更加简化：

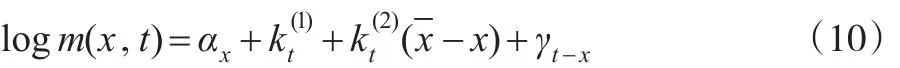
γt-x指出生年效应，与前文模型所指意义类似。

2 随机死亡率模型拟合效果的比较分析

2.1 随机死亡率模型的选择

下页表1将前文提到的随机死亡率模型进行了汇总。其中，LC模型是出现最早的随机死亡率模型且该模型不包含出生年效应；RH模型和APC模型把LC模型进一步拓展，但APC模型比RH模型更稳定。CBD模型是针对高龄人群、基于Logistic转换的双因素模型；将M7模型进一步简化，可得到M6模型和M8模型；因纳入二次年龄效应和出生年效应两个成分，使得M7模型稳定性更强；M8模型同为CBD系拓展模型，它包含了年龄-出生年效应因子；Plat模型即四因素死亡率预测模型。

2.2 模型参数的估计方法

本文在进行参数估计时，假设死亡人数D(x，t)近似服从Poisson，即：

其中，D(x,t)指在t年时x岁的人的死亡数量，用E(x,t)指在t年时x岁的人平均死亡风险暴露人数，m(x，t)与之前模型类似。为了避免空缺数据单位对参数估计的影响，本文将提前拟定权数而准许数据过度离散。Yxt指在t年时年龄为x岁的人的死亡数量。基于Yxt的一阶矩和二阶矩，可得到关系式如下：

表1 8个随机死亡率模型

其中，Φ为比例参数，wxt为权重函数，V[E(Yxt)]=E(Yxt)为方差函数。令数据缺失时的权数等于0，反之等于1。为了使模型之间的比较基础一致，本文将使用死亡率q(x，t)的模型转换成m(x，t)，如下：m(x，t)=-log[1-q(x，ty)]。这样能够对表1中的8个模型都使用m(x，t)来计算模型的极大似然估计值。

对于一个给定的模型，要将符号m(x，t)扩展成m(x，t，θ)来代表参数之间的依赖性，其中θ表示待估计的参数向量，同样地：

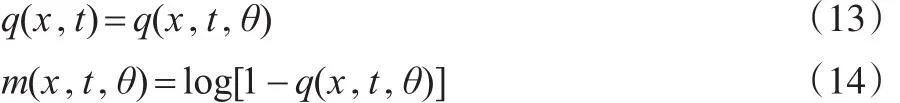
对上述8个模型进行参数估计时，使用的是极大似然估计法，具体形式如下：

最后，为了得到各参数的估计值，使用牛顿迭代法，其公式如下：

2.3 模型的选择标准

2.3.1 残差图检验

本文使用了中国1994—2013年0～89岁的综合死亡人数和平均死亡风险暴露人数数据，来更好地比较所选取的8个模型的拟合效果。图2和图3以残差图的形式，在泊松误差结构假设下，分别反映了年龄、日历年和出生年对死亡率的影响。通常按照残差分布来选择模型。依据图2和图3，可看出8个模型都捕捉到了时间效应，但是仅仅只有RH、APC、M6、M7、M8以及Plat模型反映出了出生年效应。此外，从CBD模型残差图中能够得知，其年龄残差图以及出生年残差图都呈现了波动剧烈的特征，这在一定程度上表明了年龄效应以及出生年效应并没有在其中得到反映，但是从其时间残差图得知，时间效应能够在该模型中得到有效地反映，因为其时间残差图是均匀分布在零轴两侧；LC模型也未能较好地捕捉出生年效益，因其对应的残差有轻微的波动，但该模型却很好地捕捉了年龄效应和时间效应；从残差图可看出，RH模型和APC模型的拟合程度很高，三个成分的残差在零轴两侧均匀分布，但是RH模型的拟合效果的稳定性优于APC模型。M7模型的残差图分布均匀且最接近零轴，因此该模型的拟合程度较高，优于M6模型和M8模型；与M7模型相比，虽然Plat模型的残差分布均匀，但在零轴附近的偏移程度较大，因此该模型对数据的拟合存在一定的偏差。

图3 M6、M8、M7与Plat模型的残差图

2.3.2 AIC和BIC比较法

通常，极大似然估计值的大小受模型中参数个数多少的影响，参数个数越多估计值越大，则会使模型过度参数化，可以通过惩罚过度参数化的模型来避免该问题。本文将运用贝叶斯信息准则（BIC）和赤池信息量准则（AIC）来观察添加的每一个参数对模型的极大似然估计值的影响。就比较标准而言，AIC和BIC考虑到了模型的拟合质量和简洁度，同时在比较时不必考虑模型之间有无相互嵌套关系，此外，BIC没有假设先验模型的排序。通过得出表1中的8个模型的AIC值和BIC值及其大小顺序（见表2），能够发现RH模型对中国的死亡数据的拟合程度最高，其次是Plat模型，再次是APC模型。

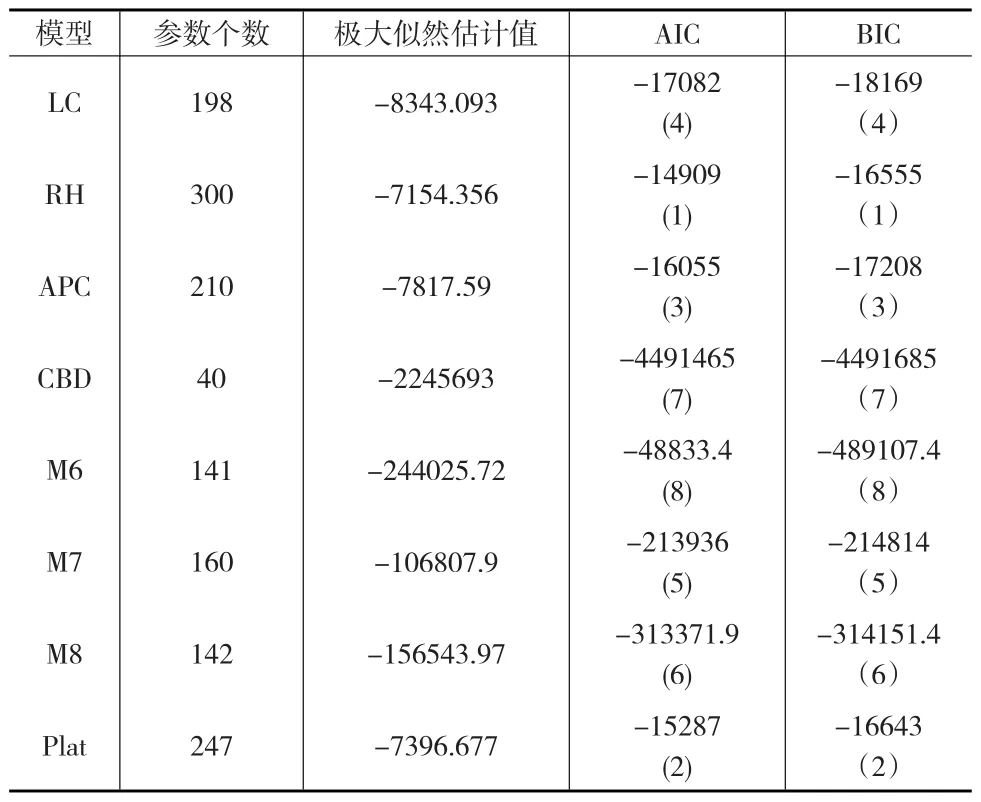
表2 8个随机死亡率模型的AIC和BIC值及其大小顺序（括号中）

2.3.3 嵌套模型的似然比检验

嵌套模型是一般模型的特殊形式。例如，在简化RH模型基础上提出的APC模型是其嵌套模型。对于嵌套模型，通常采用似然比检验的方法，该检验的原假设为嵌套模型的拟合效果好，备择假设为更一般的模型拟合效果更优。就APC和RH模型而言，设APC和RH模型的极大似然估计值分别为和，其参数估计个数分别为v1=214，v2=304。假设原假设成立，极大似然比统计量是2(-l1)，可知它近似服从卡方分布，自由度d.f.为α 为置信水平），那么拒绝原假设，得出RH模型的拟合效果更优的结论。

如表3所示，表2中的嵌套模式的模型总共有6对。通过表3可以明显发现P值都小于α，因而拒绝原假设，得出一般模型的拟合效果优于嵌套模型的结论。

表3 一般模型与嵌套模型的似然比检验

2.3.4 参数的稳定性检验

本文选取了RH模型、APC模型和Plat模型，上述三模型均为BIC值较大的死亡率模型，并使用极大似然估计法对年龄0～89岁的人进行参数估计，然后分别作出参数分布图，如图4所示。本文选取了1994—2013年和1997—2013年的中国综合死亡人口数据和综合平均死亡风险暴露数据来对上述三个模型进行参数估计。1994—2013年以及1997—2013年的数据拟合的模型中每一项的分布见图3，其中，散点使用的是1994—2013年的数据，折线使用的数据为1997—2013年。令年龄在[0,89]内取值,日历年分别在[1994,2013]和[1997,2013]内取值。

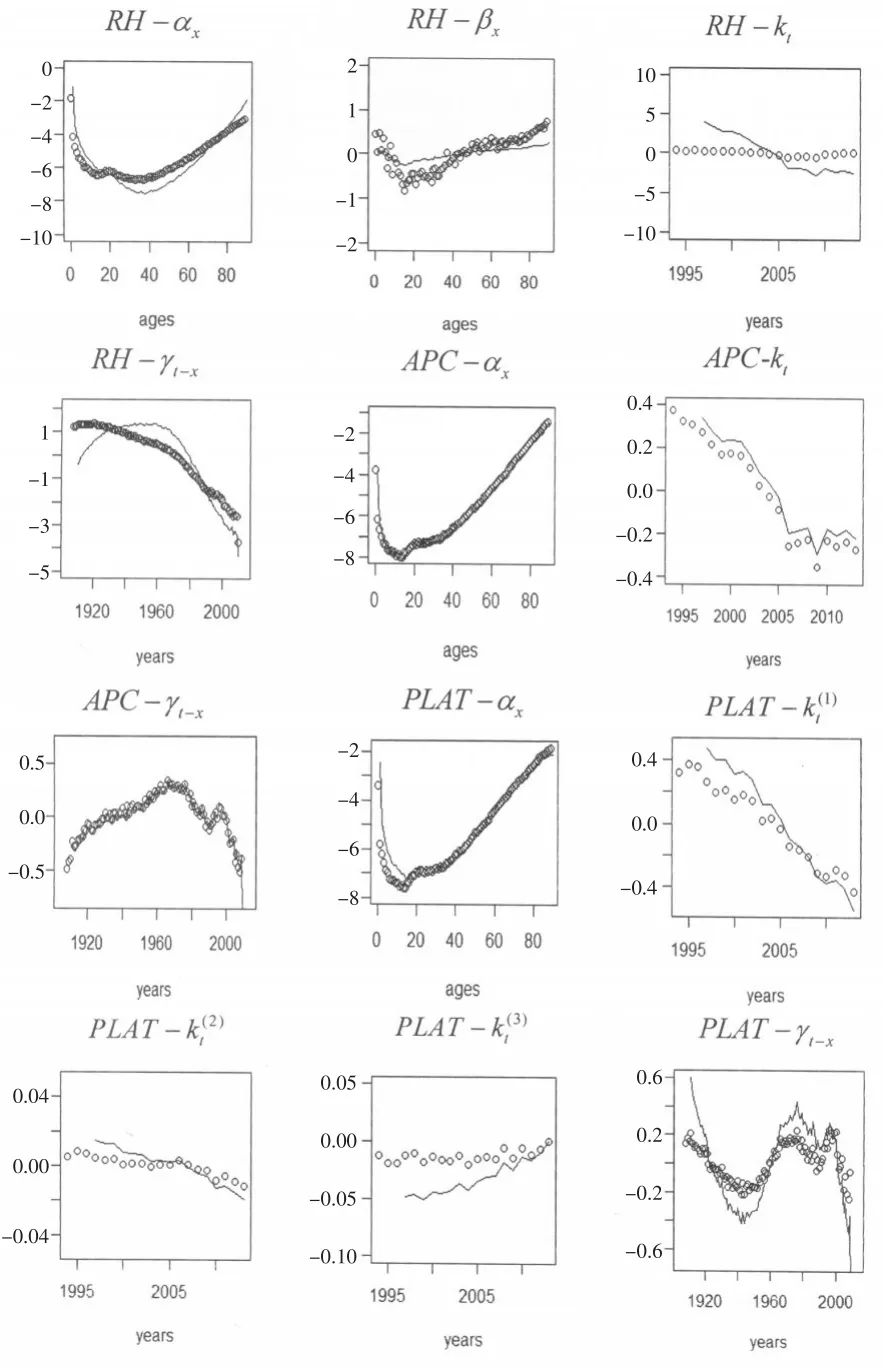
图4 RH、APC、Plat模型的拟合稳定性检验图

从上述三个模型的检验图中看到它们出生年效应显著，其出生年效应曲线在t-x≥1970时均呈现出下降趋势。

参数是否具有稳定性是衡量模型优劣的重要指标。若模型的稳定性较好，则该模型在使用不同时间段数据的情况下，得到的两组估计值曲线相吻合。对于APC、RH和Plat模型，它们的参数估计图在年龄项的拟合上较为接近，且相对稳定，即使在拟合模型参数时使用的时间段较短，其参数图也改变不大。RH模型对于出生年效应的拟合效果相对较差：1997—2013年数据拟合的出生年指数图是先上升后下降的，而1994—2013年数据拟合的指数图却有下降趋势。不同于RH模型，APC模型和Plat模型在时间段较短的情况下，其预测趋势与原图线大致吻合，故其拟合效果较优，但出生年指数因数据变少，方差变大而扩大了其取值范围。Plat模型出生年指数范围由原来的(-0.2,0.2)扩大至(-0.6,0.6)。

3 结论与建议

本文对所选取的8个随机死亡率预测模型的拟合效果进行比较与分析。发现当以残差图的形式，在泊松误差结构假设下，每个模型都捕捉到了时间效应，且除了LC模型和CBD模型外都捕捉到了出生年效应。研究表明RH模型、APC模型和M7模型拟合程度最优，而LC模型和CBD模型拟合程度较弱。就BIC检验而言，能够发现RH模型对中国的死亡数据的拟合程度最优，其次分别是Plat模型和APC模型。就参数稳定性而言，APC模型、RH模型和Plat模型的参数估计图在年龄项的拟合上较为接近，且相对稳定，预测结果较为准确。因此，在综合考虑所有的死亡率模型拟合效果后可以得出，APC模型与我国的人口死亡状况最相适应。

从以上结果能够得出，并不存在一个可以有效解决我国人口死亡状况拟合中存在的各种问题的随机死亡率模型。这不仅在一定程度上反映出难以获取人的死亡状况的发展变化规律；同时也提出了进一步的要求，需要对现有的关于人口死亡率预测的方法及模型进行优化。