低成本微惯性组件的复合标定与智能滤波方法*

王 磊,胡学东,关 英,徐九龙,郝永平

(沈阳理工大学兵器科学技术研究中心,沈阳 110159)

0 引言

微机电系统(micro electro mechanical system,MEMS)惯性传感器作为军用级和宇航级产品,可用于军事领域和抗恶劣环境要求高的场合[1]。通过算法补偿可以改善这些微惯性器件的综合性能指标,提高其精度[2-3]。误差补偿后的组件可广泛应用于旋转弹丸、无人飞行器等对体积、成本有特殊要求的微小型导航系统[4-5]。

目前,采用微惯性测量组件与其他传感器、卫星接收系统等进行组合,进行多传感器数据融合[4]、自适应滤波[5]是研究的重点和热点。应用最广的信息融合方法是扩展卡尔曼滤波(extended Kalman filtering,EKF),但当微惯导系统中系统模型和噪声统计特性存在不确定性和非先验性时,会导致EKF产生较大估计误差,甚至发散。为了克服传统EKF不足,提出了包括Unscented卡尔曼滤波、粒子滤波(particle filtering,PF)等非线性滤波方法[6],上述算法由于收敛性、计算量大等问题,较少在实时性较高的实际导航系统中应用。文中针对自主研制的小体积、低成本微惯性测量组件,提出了去除高动态旋转对低动态输入轴耦合影响的复合标定方法。结合智能控制方法和传统EKF算法,提出了智能滤波方法,根据量测噪声大小,通过人工神经网络在线调整Q和R值,体现了一定的自适应性。构建了微惯性组件导航实验系统,并采用所提方法进行了验证。

1 低成本微惯性组件复合标定

实验室自主研发的微惯导系统包括MEMS惯性组件、地磁测量模块、卫星接收模块、现场可编程门阵列核心板(FPGA)、数字信号处理器(DSP)、电源模块、接口电路板组件,如图1所示。

图1 微惯性导航系统

微惯性组件构成的惯导系统是一个时变系统,其性能随时间受到影响,其误差主要包括零偏、标度因数、非正交误差等。陀螺仪的误差模型为：

(1)

(2)

主对角线元素ki(i=x,y,z)为标度因数,σjk(j,k=x,y,z)为非正交安装误差。加速度计的模型如下:

(3)

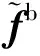
(4)

矩阵Ce=CsfCnoCsm、Csf、Cno、Csm分别代表了标度因数误差、非正交和失准角误差和软磁干扰影响。ε向量表示磁干扰的噪声项。

基于微机电系统的器件普遍存在精度不高,漂移较大等制约,特别在弹载高动态环境下,需要对相关器件测试,标定和补偿提出严格的要求。在初始标定中利用单轴速率转台和三轴转台,采用多位置静态和动态结合的标定方法去除零偏和标度因数的影响。针对加速度计,根据三轴加速度计分量等于重力加速度的原理,采用18位置的标定方法,包括6个正交位置及分别倾斜于水平面成30°和45°角的12个斜置位置。分别放置陀螺仪的敏感轴x、y、z朝上或朝下,转台分别顺时针和逆时针旋转。标定实验中陀螺仪量程选择±10～±300°/s,标定间隔为±10°/s。根据采集数据,由正负位置相消法确定常值零偏等参数。为保证整个量程内误差最小,采用最小二乘法和均值法对确定性误差进行估计。标定后,为验证陀螺仪补偿结果,选定任意角速度进行精度测试,共29个测试档位,测试结果见图2。

图2 陀螺仪的精度测试

陀螺仪敏感轴x,y,z标定后的RMSE分别为0.020 4°,0.045 9°和0.015 4°。磁力计采用12位置标定进行标定[7],得到的确定性误差见表1。

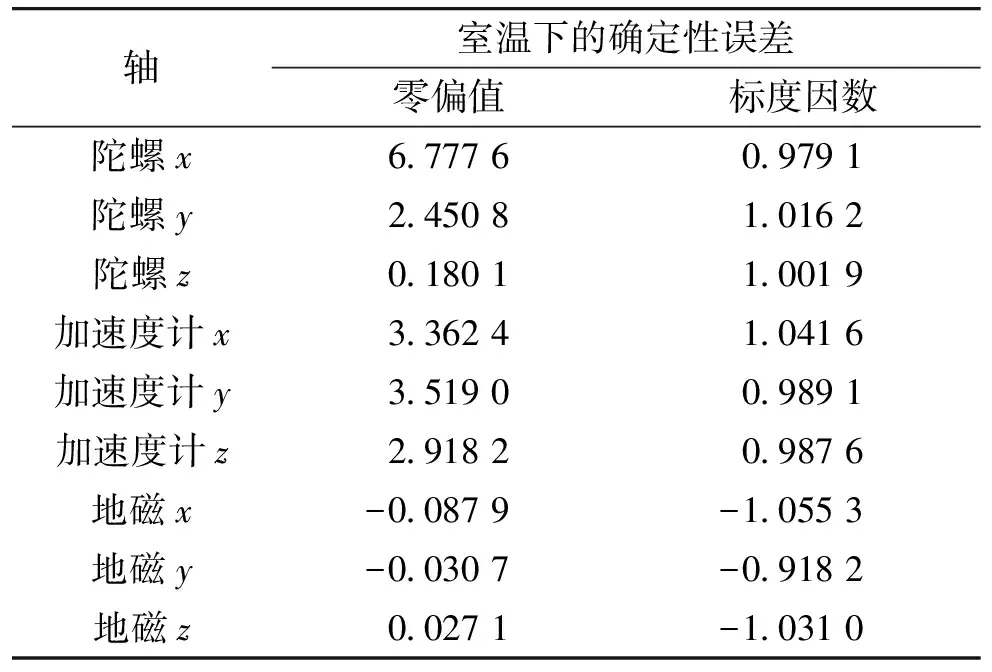
表1 微惯性组件和磁组件的主要标定误差

表1中,陀螺仪、加速度计和地磁传感器的零偏单位分别是(°)·s-1,g,Gs。考虑到微惯性组件在旋转弹丸应用中滚转轴高动态变化、俯仰和偏航低动态变化的情况,提出了复合标定方法对输入轴失准角进行解耦。具体方法如下:

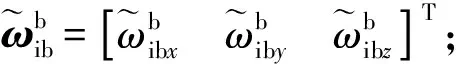
首先在三轴转台上分别设置内框、中框,模拟弹丸滚转角和俯仰角变化。其中,内框的预设数据模拟弹丸在不同的滚转速率下连续变化。考虑到三轴转台内框速率限制,滚转角速率设定在0～3 r/s内连续变化。同时中框轴按照间隔5°,在±60°俯仰角变化范围内,共25个档位下进行实验测试。考虑到真实滚转弹丸的偏航角变化较小,实验中模拟偏航角的外框设定在固定位置。实验采集得到的多组陀螺仪的模拟数据用做ANN的训练样本。

训练过程中,网络权值离线调节,安装于微惯性组件中不同输入轴陀螺仪的输出和不同输入轴耦合系数的非线性映射关系通过ANN来确定经过多次实验验证,网络隐层设定30个节点,训练次数110次可以满足实验的测试精度。

为了验证复合标定方法有效性,选取了一组与训练实验中不同的模拟弹丸旋转的姿态数据进行了测试,误差补偿结果见图3。

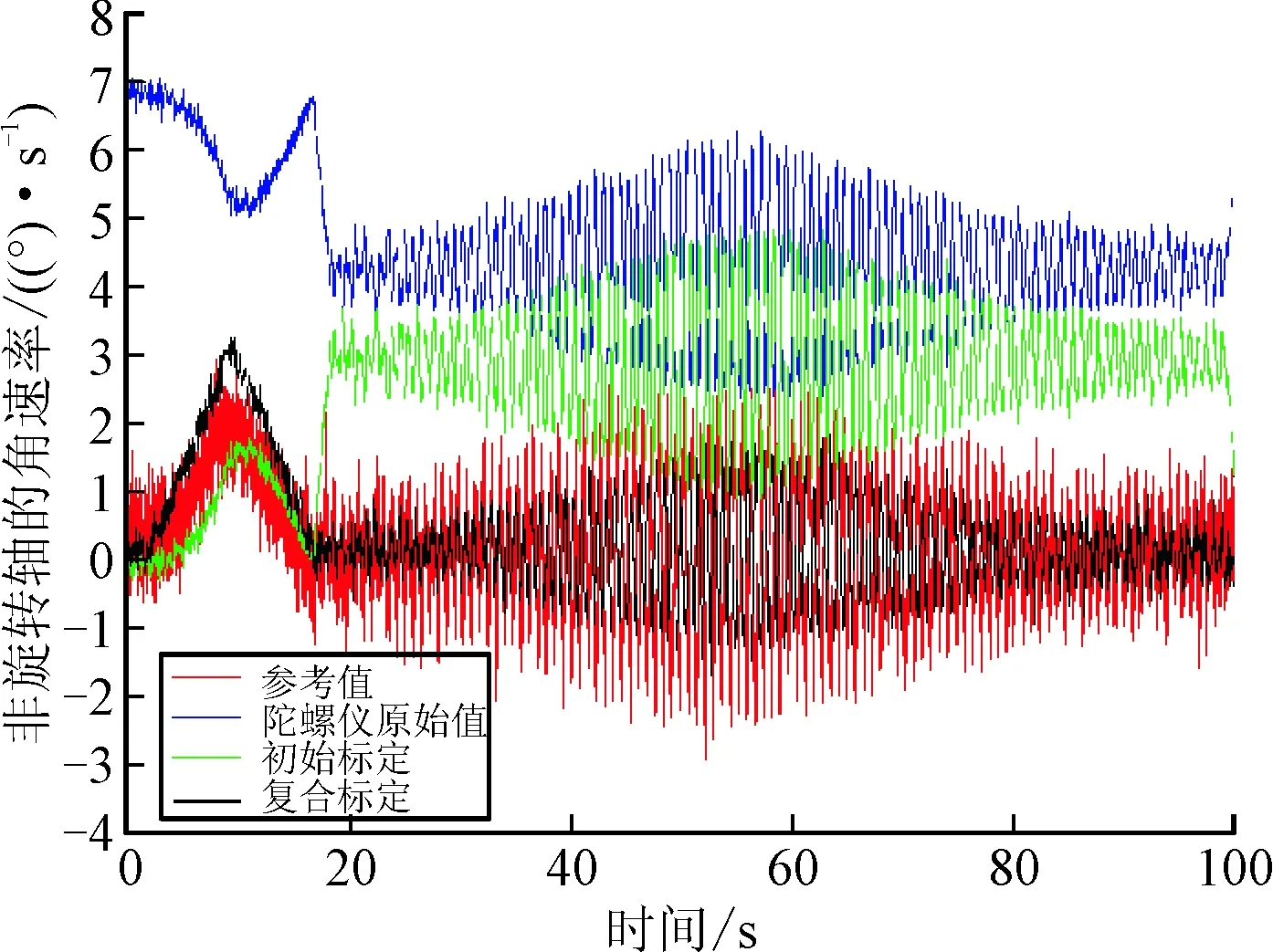
图3 陀螺仪复合标定结果

图3中为旋转轴在高动态变化条件下,任一非旋转轴的输出角速率。在弹丸姿态模拟测试中,由于旋转轴高动态旋转对低动态输入轴的耦合影响,原始采集数据较参考值有较大偏差,采用最小二乘法的初始标定后有一定改善。采用基于ANN的复合标定后,校定了新的耦合系数,误差补偿结果较好。初始标定与复合标定中耦合系数的对比见表2。

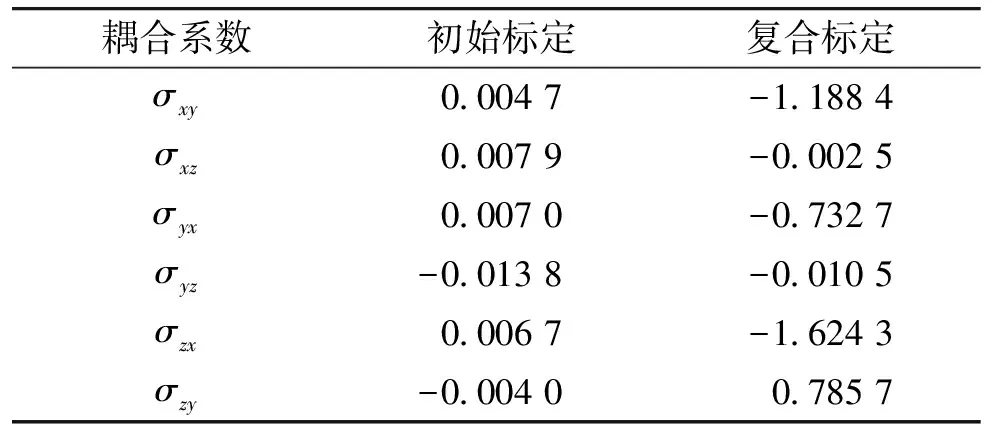
表2 初始标定与复合标定耦合系数对比

由对比可见,高动态环境下耦合系数通过复合标定补偿后,有效地去除了高动态旋转轴和低动态非旋转轴的耦合影响,取得了较好的误差补偿效果。

2 智能滤波方法

2.1 系统模型

低成本微惯性组件经过标定与误差补偿后,与卫星接收机构建了简易的组合导航系统应用于弹丸等瞬时飞行载体的位姿解算。为了取得较好的位姿精度,选用位置、速度和姿态误差以及载体坐标系下的陀螺漂移作为导航系统状态变量表示为:

(5)

为了避免系统误差模型中依赖无干扰条件下载体运动参数的理论值,在某些重要参数计算时会受到较大影响,采用处理过的外部速度信息作为阻尼引入惯导误差方程,简化模型为:

(6)

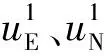
(7)

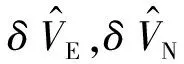
(8)

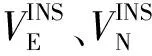
2.2 滤波参数的在线调整

滤波器中考虑了微惯导系统的系统模型和噪声统计特性存在不确定性和非先验性条件下的影响。系统和量测噪声的初始值及初始协方差矩阵由Allan variance方法确定[8]。为了评估滤波器性能,定义反映量测噪声影响的目标函数Jt,k为:

(9)

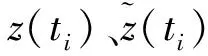
图4 低成本微惯导组件导航系统

3 微惯导系统试验研究

实验测试平台包括实验室开发的FPGA/DSP导航样机、电源模块、低成本微惯性组件、卫星接收机等。此外,为了进一步验证所提方法,采用荷兰Xsens Motion Technologies公司的姿态航向参考系统MTi作为参考进行姿态比较,实验系统见图5。

图5 低成本微惯性组件车载实验系统

车载测试实验中选择了沈阳理工大学校园中不同路段为测试路段,进行了多次跑车试验。试验中分别采集了微惯性组件的数据,MTi传感器与参考姿态数据,FPGA/DSP导航样机对采集的试验数据进行处理、解算。实际卫星轨迹和导航系统解算的轨迹见图6。

由图6可见,IKF方法能够预测经纬度误差,算法估计的经纬度与卫星实测的轨迹基本吻合,经纬度最大误差控制在1.98×10-6rad,1.14×10-6rad。为验证所提算法的滤波效果,选取估计的姿态误差角进行对比,图7为提出IKF方法与传统EKF方法对北向姿态误差角滤波的结果。

图6 车载轨迹

图7 北向估计的误差角

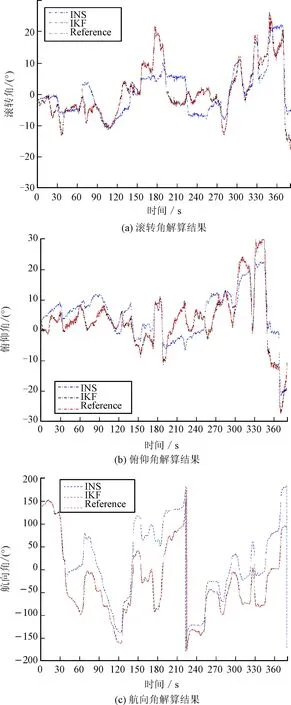
图8 姿态角变化

系统中采用MTi提供的姿态信息为参考值,由图对比可见,单纯惯导系统由于受到低成本陀螺仪和加计漂移误差等影响,随着时间积累,姿态误差逐渐变大,滚转和俯仰姿态最大误差为5°～6°,航向最大误差50°以上。对比之下,IKF算法依靠卫星提供的精确位置和速度信息作为观测值,在姿态更新方程中引入了滤波后的精确外部速度信息作为阻尼,避免了受到单纯惯导系统较大计算误差的影响,求解过程的稳定性和精度有较大提高。此外,在噪声统计信息非先验条件下,通过协方差矩阵参数的在线调整,有效地提高了滤波器的辨识精度,得到的俯仰和横滚精度控制在0.2°之内,航向精度由于受到低成本微惯性器件误差的影响,控制在3°之内。通过有效滤波,估计的姿态角达到了MTi同等级的姿态精度。

4 结论

针对低成本微惯性组件在弹载等导航系统中应用问题,提出了对微惯性组件的复合标定方法,校定了高动态环境下的耦合系数,补偿了90%的系统误差。结合智能控制和EKF滤波方法,提出了自适应性的IKF方法。系统更新方程中建立了外部速度阻尼作为反馈量,有效地抑制了内部解算误差的影响。通过人工神经元和模糊控制器有效调节,对未知的噪声特性进行实时修正,有效地提高了噪声辨识的精度。实验结果表明,采用所提方法,俯仰和横滚精度控制在0.2°之内;航向精度由于受到低成本微惯性器件误差的影响,控制在3°之内,达到了与商用AHRS相同的姿态解算精度。