不同代际关系家庭的家电配置偏好度研究
郑思源,韩跃峻,辛洁晴
(1.上海交通大学电气工程系,上海 200240;2. 国网上海市北供电公司,上海 200072)
0 引 言
我国正在实施的新一轮电力市场改革以电力零售市场的开放为基本特征[1]。在该背景下,电力零售商将更注重通过需求侧管理(demand side management, DSM)措施提高客户粘合度。家电配置偏好度反映某类家庭选取某种家电配置方案的概率。据家电配置偏好度可获知各类家庭最为典型的几种家电配置情况,使得电力零售商可为设计中的负控方案或电价措施开展家电运行模拟和移荷/降载潜力评估,进而提出差别化的、适应不同家庭用户群的DSM措施。
目前对家电配置方案的研究多局限于对家电类型组合情况的研究。例如,文献[2-3]在进行DSM研究时,考虑了空调、热水器等常用家电类型并对这些家电类型的组合方案直接进行了假设;文献[4-5]在进行家庭用电负荷曲线仿真时,在居民对各类家电拥有率调研数据的基础上,采用蒙特卡洛方法随机产生了家电类型意义上的配置集。上述研究均未考虑家庭在家电功率规格选择上的差异,这对实施家电运行方案模拟和DSM效果评估而言是不够的。
另一方面,现有文献鲜有对家电配置方案的分类研究。一些文献探讨了家庭居住面积对部分家电规格选择的影响[6],但家电规格的选择不仅仅与居住面积有关,有些与家庭人员数和人员结构的关系更为密切。代际关系可描述家庭在人员数、人员结构上的差异,同时也间接影响家庭居住空间数和居住面积,故而能更全面地影响家电配置情况。从代际类型的角度对典型家电配置方案实施分类研究,有助于电力零售商更准确地划分用户群体,开展DSM措施的差别化设计和应用。
鉴于此,本文开展不同代际类型家庭的家电功率配置偏好度研究;并且,鉴于实施大规模调研并获得可靠调研结果的难度较大、扰民度较高,将对家电配置偏好度问题提出一种非直接调研的方法。
1 代际关系、家电配置及其偏好度的定义
1.1 代际关系
代际关系描述家庭成员中有几代人及其之间的亲属关系。据文献[7],家庭代际关系主要分为单代、两代、三代、三代以上4类,考虑到三代以上家庭占比不高,本文仅考虑前3种,但考虑到用电行为的差异,单代家庭又分为单代一型(独居家庭)和单代二型(夫妻核心家庭),故共有4类代际关系,下文分别用下标1~4表示。单代一型的家庭成员为1人,单代二型为2人,两代为3~4人,三代多为4人及以上。代际关系决定了家庭人口数、间接影响家庭居住面积,从而对家电配置有决定性影响。
1.2 家电配置集
根据文献[8]对我国家庭常用电器的调研,本文考虑13种常用家电,分别为日光灯、电视、电冰箱、洗衣机、空调、电饭煲、饮水设备、热水器、抽油烟机、微波炉、电吹风、电脑、路由器等。以下用下标k表征家电类型。
DSM项目设计时需关注不同家庭对各类家电功耗档位选取上的差异。为此,定义家电配置方案为家庭中各电器所选取的档位的集合,以下记第s个家电配置方案为Es={e1,s,e2,s,…,en,s},其中n=13为所考虑的家电种类数,ek,s为该配置方案中对第k种家电的档位选择。家电配置集是家电配置方案的集合。
1.3 家电配置偏好度
家电配置偏好度是某类家庭对某种家电配置方案的喜好程度。本文用取值范围为0~1的量来描述这种偏好度,并设各类家庭对所有家电配置方案的偏好度之和为1。为此,家电配置偏好度也可看做某类家庭在所有家电配置方案中选择某种特定配置方案的概率。
定义第i类家庭对第k种家电选择第j个功率档位(对拥有多台的家电为档位组合)概率为γi,k,j,称之为家电档位偏好度,则第i类家庭选取家电配置方案Es的概率Pi,Es为该类家庭对此配置方案中各家电档位偏好度的乘积,即成立
(1)
2 方法的基本思想和流程
鉴于各类家庭对各种功率档位家电的偏好度最终决定了各功率档位家电在销售市场的占有率,而不同功率档位家电销量占有率的调研和统计相对比较简单,故本文运用拟合的思想,提出一种据各功率档位电器市场占有率析构出家电配置偏好度的方法。具体流程为如图1所示。
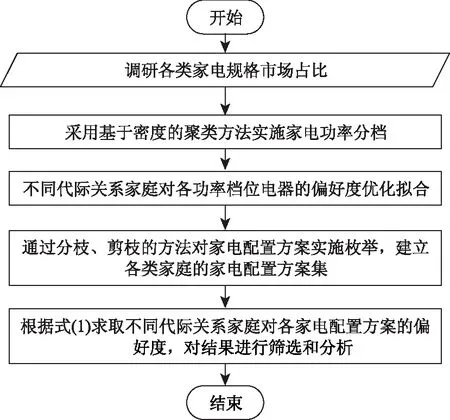
图1 不同代际关系家庭家电配置偏好度研究流程图Fig.1 Flow chart for the study on household appliance configuration schemes preferences of families with various generations
① 家电功率分档:同种家电因品牌、型号差异,用电功率有所差异,但设计DSM项目时并不需要考虑过于多、杂的家电功率。为此,在市场调研的基础上,采用基于密度的聚类方法对各种家电实施功率分档,并统计出各档位的市场占比和典型功率,同种家电不同功率档位往往对应了不同的用户群(例如300~400W的电饭煲通常对应适合1~2人使用的2L电饭煲,750~850W则对应适合4人左右的4L电饭煲)。
② 不同代际关系家庭对各功率档位电器偏好度的拟合:用各类家庭对各功率档位电器的偏好度描述各功率档位电器的市场份额,进而根据各类家庭占比和各功率档位电器的市场占比,构建市场占比拟合度最优化模型,求解得到各类家庭对各电器档位偏好度的拟合值;
③ 建立家电配置方案集:通过分枝、剪枝的方法对家电配置方案实施枚举,建立各类家庭的家电配置方案集,并根据式(1)求取各家电配置方案的偏好度,对结果进行筛选和分析。
3 家电功率档位划分方法
本文调研了苏宁易购、海尔、美的等多个主流电器经销商的网上旗舰店,对各电器进行了各品牌各型号的单机功率和销售量统计。附表A1列出了经市场调研获知的13种常用家电的功率范围。鉴于DSM项目设计时主要关注对移荷、节电影响较大的大功率电器,在家电功率分档中只考虑功率较大的空调、电饭煲、饮水设备、电热水器4种家电,其余家电只考虑配置/不配置两种情况,功率不予分档(微波炉、电吹风虽功率较大,但每个家庭通常只配置一台,且功率规格差不多,故不分档)。功率分档的几类电器的分档方法可归结为如下几类:
① 饮水设备、热水器:有几种常用的技术类型,且不同技术类型的用电功率迥异。例如,常用的饮水设备包括非蓄热式电热水壶和饮水机,热水器包括燃气热水器和电热水器。对此,先按技术类
型分类,随后对同种技术类型再实施聚类。
② 电饭煲、空调:不同技术类型的功率差别不大,直接采用聚类方法实施功率分档。
对上述各种家电做出单机功率散点图(以电饭煲为例,如图2);再采用基于密度的DBSCAN (density-based spatial clustering of applications with noise)聚类方法[9]实施功率档位的聚类分析。该方法以数据集在空间上的密度为依据进行聚类,无需提前设置簇的数量,且能够发现任意形状的簇,应用较为广泛。聚类时先任取一个点作为出发点,找出与其距离不大于某个阈值(称作扫描半径r)邻近点,若邻近点数量小于最小包含点数的阈值Nmin,则所选出发点标记为噪声点,反之则将该出发点与其邻近点作为一个簇;随后以相同的方法处理该簇内所有未被访问的点,从而对簇进行扩展;如果簇内所有的点都被标记为已访问,则继续用同样的算法处理簇外未被访问的点,直至所有点都被归入了某个簇或者标记为噪声点,算法终止。
聚类完成后,以每个类别中所有样本的平均单机功率作为该档位的典型单机功率,最后对聚类所得各档位电器统计市场份额,所得结果如表1。

图2 基于密度聚类法得到的电饭煲分档结果Fig.2 Rice cooker power clustering result based on the density clustering method

家电档位I档位II档位III规格范围典型功率/W市场份额/%规格范围典型功率/W市场份额/%规格范围典型功率/W市场份额/%电饭煲2.5L及以下41226.743~4L75254.275L及以上89218.99电热水器40L1 77515.6550~60L1 92571.1380L及以上2 36713.16空调小1~大1匹2 66941.191.5~大1.5匹3 51143.432~3匹5 89414.83饮水设备电热水壶1 50077.11饮水机30522.89---
4 各类家庭对各功率档位电器偏好度的拟合
根据家庭对某种电器拥有数量的不同,拟合的方法略有差别,分为如下两种情况。
4.1 通常只拥有单台的电器
此类家电包括电饭煲和电热水器。由各类家庭的占比及其对该档位电器偏好度的乘积之和可以推得每种档位家电的市场份额,即成立
(2)
其中
(3)
式中:αi为第i类家庭所占比重;zk,j为第k种家电里第j档位电器的市场占有率。
各类家庭对第k种家电各档位偏好度的拟合结果应该使得按式(2)计算所得的市场份额与各档位家电实际市场份额足够接近。综合考虑3种档位的情况,可构建如下最优化问题
minf=
(4)
s.t.
① 同类家庭对各档位家电偏好度的相对关系
电热水器和电饭煲的功率与家庭人数直接有关,故:单代家庭选取功率最低的I档电器的概率最高,选取功率最大的III档电器的概率最低;两代家庭选取I档和III档电器的概率均小于II档电器;三代家庭选取I档电器的概率最低,III档电器的概率最高。即
(5)
② 同种档位家电为不同类型家庭选取的概率的相对关系
随着家庭人数的增加,家庭对I档电器的偏好度降低,对III档电器的偏好度升高,即有
(6)
③ 决策变量取值范围约束
0≤γi,k,j≤1,i=1,2,3,j=I,II,III
(7)
求解上述问题,即可获得偏好度γi,k,j的拟合值。
4.2 通常可能拥有多台的电器
此类家电包括饮水设备和空调。由于每一家庭可能同时拥有多台,需考虑电器档位的组合情况。以下用I-II表示家庭拥有一台I档和一台II档的组合情况,其余类推。考虑多台电器组合情况时,第k类家电第j种档位的市场份额可用下式计算
(8)
式中:Mi,k表示第i类家庭拥有多台电器k的功率档位组合的可能情况的集合;ci,k,m,j表示第i类家庭对于电器k的档位组合m中j档位电器的数量。
4.2.1 饮水设备
通常一个家庭中同样的饮水设备不会超过1台,故对饮水设备的档位选择存在I、II和I-II 3种情况。各类家庭对饮水设备档位(组合)拟合问题为
(9)
s.t.
① 不同类型家庭之间对饮水设备档位(组合)偏好度的相对关系
人口数量越多,热水的需求量也越高,对I档电器的偏好度越小,对I-II档组合的偏好度越高。即
(10)
② 每类家庭对各档位组合的偏好度之和为1
(11)
③ 偏好度取值范围约束
0≤γi,k,m≤1,i=1,2,3,4
(12)
4.2.2 空调
空调安装的空间主要是起居室和卧室(也可布置成书房),档位配置主要决定于这些居住空间的面积。根据文献[10](附表B1)中根据不同经济水平而列出的各类居住空间的典型面积,并考虑到起居室制冷空间通常还包括餐厅、玄关等连通区域,起居室的制冷面积的典型值有18m2、22m2、28m2、35m24种,卧室的典型面积为9m2、12m2、15m2、18m24种。对照各档位空调最大制冷面积表(附表B2[11])可知,卧室安装I、II档空调较为合理,此外主卧面积一般要大于次卧面积,故最多仅有一个卧室会安装II档空调,其余安装I档空调;起居室安装II、III档空调较为合理。又根据代际特点,对单代家庭考虑1~2个居住空间,两代家庭2~3个居住空间,三代家庭3~4个居住空间,故家庭的空调最大台数为代际数加1。由此列出4类家庭可能的空调档位组合分布,如附表B3所示。相应地,可写出空调档位(组合)方案偏好度的拟合问题为
(13)
s.t.
① 典型居住空间组合对应空调档位组合方案的约束
不同居住空间组合的合理性存在差异。文献[12]对各居住空间相对尺度的合理性进行了分析,并指出居住空间应相对均衡(即面积差距不会很大)。根据该文分析结果做如下合理约束。
a.单代家庭空调档位组合方案偏好度相对大小关系
单代家庭只装1台空调时,选择I档或II档的概率高于III档;安装两台空调时,两个居住空间差距较大的可能性较小,故I-III组合的偏好度相对较低,并且I-I、I-II对应的居住空间组合的概率比II-II、II-III对应的居住空间组合的概率高。从而有
i=1,2
(14)
此外单代二型和一型相比,因人数较多,使用两个带空调的居住空间的概率较大,即
γ2,k,m≥γ1,k,m,m∈
{I-I,I-II,I-III,II-II,II-III}
(15)
b.两代和三代家庭空调档位组合方案相对大小关系
对于两代和三代家庭,因家庭人数较多,只装1台空调时选择III档的概率较大;安装多台空调时,据居住空间大小相对均衡的原则,安装1台III档空调、其余空间均安装I档空调的概率最低。从而有
i=3,4
(16)
min(γi,k,I-I-I-I,γi,k,I-I-I-II,γi,k,I-I-II-II,γi,k,I-I-II-III)≥
γi,k,I-I-I-IIIi=4
(17)
② 居住空间数和代际关系的关系约束
空调数不小于代际数量时偏好度较高,空调数量小于代际数量时偏好度较低,故而有
(18)
式中:M4,k,3表示三代家庭(第4类家庭)安装3台电器k的档位组合集合,其余类推。
其余约束条件同式(11)~(12)。
5 家电配置方案的枚举
理论上需对各电器的所有档位进行枚举,各类家庭可能达到的配置方案数如表2所示(表中未列电器的配置方案数均为1)。但实际上,在设计DSM措施时,只需考虑每类家庭最典型的几种家电配置方案即可。因此,实施如下的分支-剪枝过程:
① 将需要枚举的家电按照组合数量从小到大进行排列,以单代一型家庭为例,枚举的顺序依次为电饭煲、饮水设备、热水器和空调;
② 按照排列的顺序,采用分枝法,首先建立电饭煲的I、II、III档分枝,随后在这3个分枝上继续分别考虑饮水设备的I、II、I-II档分枝,依此类推;
③ 在分枝的过程中,每进行一次分枝操作就计算根据当前各档位组合偏好度的乘积,若该乘积小于一定的阈值ε,则进行剪枝操作,转到下一个分枝的枚举过程,最终得到偏好度高于一定阈值的所有可能的家电配置方案。剪枝阈值ε可据最终要考察的典型家电配置数及其覆盖的居民用户比重来决定,ε值越大则典型家电配置数和相应所覆盖的用户数越少。

表2 不同代际家庭中可能达到的配置方案数Tab.2 Number of household appliances configuration schemes of families with various generations
6 算例结果
采用MATLAB最优化工具箱编程,对第4节中各优化问题进行求解。
6.1 家电档位偏好度的拟合结果
优化所得各类家庭对各种电器各档位的偏好度如表3所示。
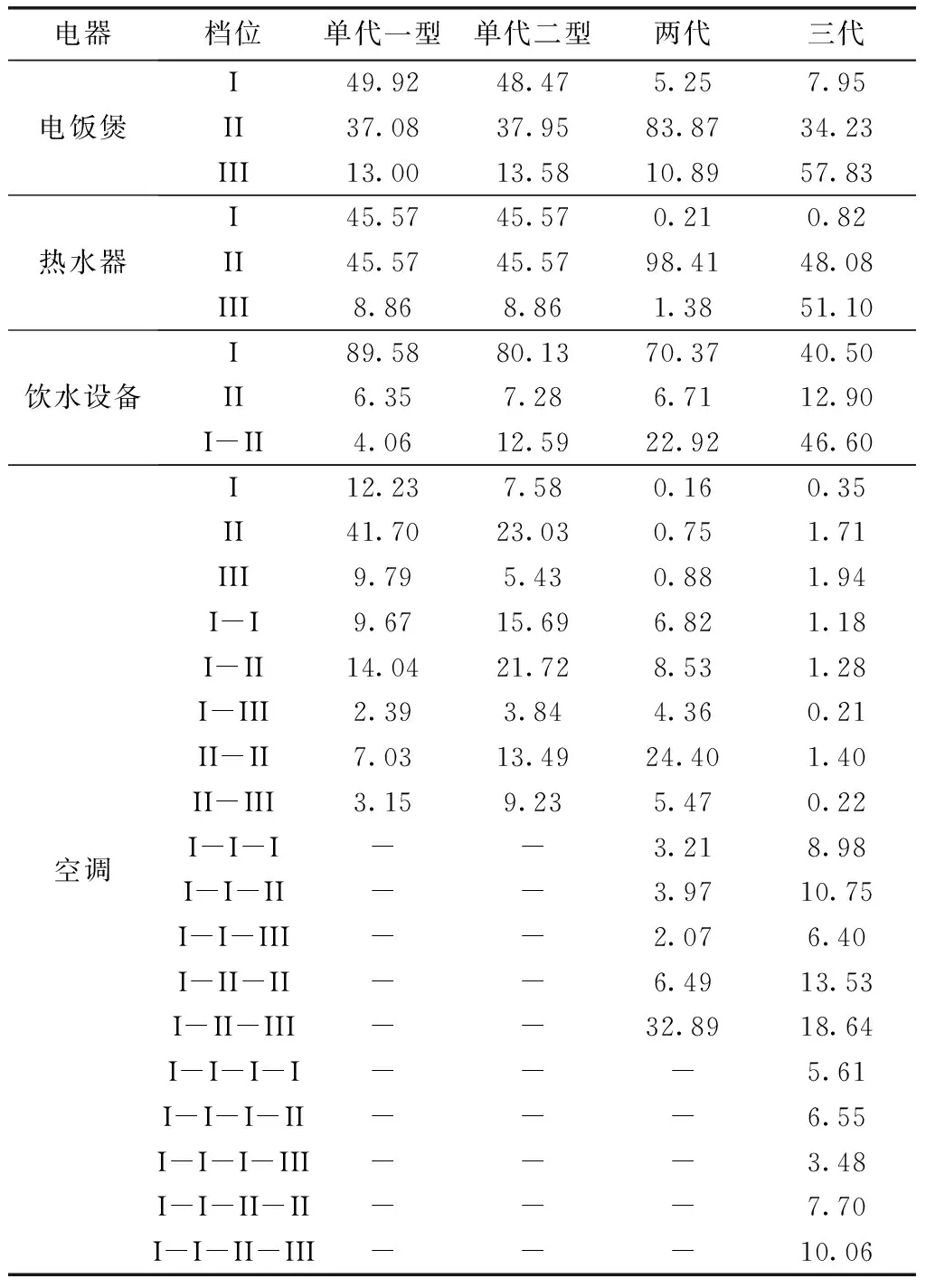
表3 不同代际家庭对各家电各档位的偏好度拟合结果Tab.3 Household appliance power size preference fitting results of families with various generations %
从计算结果来看,各类家庭的电器档位偏好度存在如下特点:
① 在单机配置和运行的电器中,对电饭煲和电热水器,单代家庭对第III档的偏好度显著小于功率较小的I和II型、且I型和II型的偏好度比较接近,两代家庭对于II档电器的偏好度远高于其他两个档位,三代家庭选择II、III档电器的概率远高于I档电器。上述结果与这些设备功率选型与家庭人口数直接相关、人口越多功率越大的规律相吻合。
② 饮水设备中,两类单代家庭只使用非蓄热式电热水壶的偏好度远高于其他两种配置情况,两代和三代家庭则或者只使用电热水壶、或者同时配置电热水壶和饮水机,很少仅配置饮水机。这与电热水壶用途更为广泛,从而市场销量远高于饮水机的情况相符。
③ 对于空调,单代一型家庭主要偏向于II档家电,单代二型家庭偏向与II档或者I-II组合;两代家庭偏向于II-II以及I-II-III组合;三代家庭的偏好度较为分散,是因为其档位组合数量较多,但是对I-II-II和I-II-III组合的偏好度相对较高。上述结果与各类家庭的典型居住空间面积组合相对应。
6.2 家电配置方案及其偏好度
为考察居民用户占比达到90%的家电配置偏好度分布情况,取剪枝阈值ε=10-3,按第5节的方法对各类家庭的家电配置方案进行枚举,计算得到4类家庭对于各自家电配置方案的偏好度,依照从大到小排列。以单代一型家庭为例,剪枝后得到109种家电配置方案,偏好度分布情况呈“L”形(如图3)。从图中可见,偏好度排名较高的几种家电配置方案偏好概率的点较为稀疏,随后各点之间间距变小,分布逐渐密集,说明本方法可有效筛选出偏好概率明显较高的家电配置方案。各类家庭偏好度排名前5的家电配置方案如表4所示。
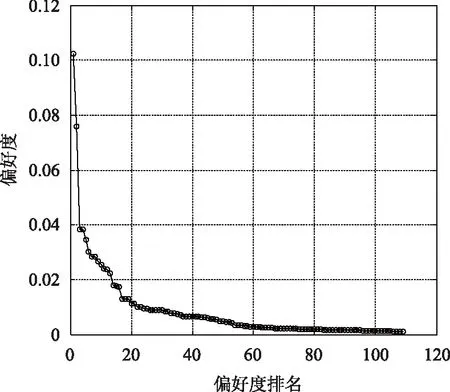
图3 单代一型家庭家电配置偏好度分布图Fig.3 Household appliance configuration scheme preference distribution of single generation family I
7 结束语
本文在对主流家电各功率档位电器市场占有率实施市场调研的基础上,采用DBSCAN聚类法对各类家电实施了功率分档;随后采用拟合思想,提出据市场占有率析构出不同代际类型家庭对各种家电各功率档位偏好度的方法;进而通过分枝、剪枝过程获得各类家庭常见的家电配置集,并评估出各类家庭对各家电配置方案的偏好度。算例验证了方法结果的合理性。

表4 不同代际家庭偏好度最高的5种家电配置方案Tab.4 Top 5 Household appliance configuration schemes of families with various generations %

