基于混合调制策略的MMC-UPFC谐波特性改善研究
梅 军,何梦雪,王 创,李 鹏,刘建坤
(1.东南大学电气工程学院,江苏南京 210096;2.国网江苏省电力公司电力科学研究院,江苏南京 211100)
0 引 言
统一潮流控制器(unified power flow controller,UPFC)是目前综合功能最为强大的柔性交流输电系统装置,集电压调控、阻抗补偿、相角调节及潮流控制等功能于一体,对提高电力系统的稳定性有着重要作用[1-2]。模块化多电平换流器(modular multilevel converter, MMC)代表着第三代直流输电技术的发展方向,相对于两电平和三电平换流器等拓扑结构,MMC具有制造难度低、开关损耗小、波形质量高、可扩展性强等优势[3-4]。
鉴于MMC在柔性直流输电领域的研究基础和工程经验[5],越来越多的研究已将其推广至柔性交流输电领域,典型之一便是UPFC装置。将MMC技术应用于UPFC工程,是UPFC技术应用的跨越式发展[6]。
在MMC-UPFC中,控制系统根据有功、无功功率及电压等控制目标指令值决定串联侧补偿电压Upq,调制比m表示Upq的峰值与1/2的UPFC直流侧电压之比。当系统所需串联补偿电压较低,m较小时,MMC逆变输出电压包含的电平数较少,将引入较多的谐波成分,影响电压质量。
针对该问题的已有研究较少,文献[7]提出一种直流降压法,当串联补偿电压调制比一定时,通过降低直流侧电压,同时配合并联变压器分接头的调整,使得交流侧输出的阶梯波电平数增多,可以在一定程度上减少谐波含量。该方法有一定的谐波改善作用,但若直流侧电压降低过多,将导致电路性能恶化,线路电压损耗增大等。文献[8]提出可以通过改变线路的无功功率以提高串联补偿电压调制比,但由此方案得到的系统级控制策略将更加复杂。有研究提出将特定谐波消去调制技术[9]和空间矢量脉宽调制[10]应用于UPFC的逆变器控制中,能够减小输出电压畸变率,提高直流电压利用率,但随着电平数的增多,该方法存在动态性能差、计算量大、实现复杂的弊端。
本文以最近电平逼近调制(nearest level modulation,NLM)与引入虚拟循环映射(virtual loop mapping,VLM)载波层叠正弦脉宽调制(carrier disposition SPWM, CDPWM-VLM)为基础,提出了一种新型的混合调制策略。一方面,NLM调制具有低开关频率和低开关损耗的优点,在较高调制比下已经具有良好的谐波特性,而低调制比下采用NLM将带来很大的谐波含量,影响电压质量;另一方面,CDPWM-VLM利用器件的高频开通和关断来减少谐波含量,在低调制比下仍然可以保证输出电压具有良好的谐波特性,但若单纯采用CDPWM-VLM,在高调制比的运行状态下将会带来不必要的开关损耗。因此,将二者的优势进行结合,劣势进行互补,从而获得MMC-UPFC更大运行范围内(表现为调制比的变化)良好谐波特性。并结合南京西环网220kV UPFC工程进行案例分析,验证所提出混合调制策略的适用性和有效性,对于研究并改善UPFC串联侧输出电压的谐波特性和电能质量具有重要的意义,也为今后MMC-UPFC的发展应用提供一定的参考。
1 基于MMC技术的UPFC
1.1 MMC-UPFC的基本结构和工作原理
MMC采用子模块(sub-modular, SM)级联的方式,单个子模块通常采用半个H桥结构。每个桥臂由N个子模块和一个串联电抗器L0组成,一个相单元由上下两个桥臂组成。
MMC-UPFC由并联补偿的静止同步补偿器和串联补偿的静止同步串联补偿器相结合而成。并联侧与串联侧换流器均采用MMC结构,二者共用直流侧,背靠背连接。并联侧MMC在补偿系统无功的同时,向直流侧及串联侧MMC提供有功功率。串联侧MMC通过串联变压器向线路注入可调的电压Upq,从而实现对线路有功、无功功率的独立控制。其中,Upq在零到额定值之间任意可调。
1.2 MMC调制技术
1.2.1 最近电平逼近调制技术
NLM具有动态响应速度快、易于硬件实现以及开关损耗小等优点,在多电平换流器中得到了广泛的应用[11]。其基本原理为:通过控制MMC一个相单元内上下桥臂子模块的对称互补投入,使得交流侧输出最接近的电平瞬时逼近调制波,如图1所示。

图1 NLM调制原理Fig.1 Principle of NLM
该调制方式的缺点在于各个子模块的开关频率不固定,损耗不均衡,且当输出电平数较少时,存在控制精度低,谐波含量大的缺点。
1.2.2 载波层叠调制技术
CDPWM通过N条在垂直空间平均分布的幅值、频率相同的锯齿载波与调制波相比较,产生N个子模块的阀级控制信号,如图2所示。

图2 CDPWM调制原理Fig.2 Principle of CDPWM
常用的PWM调制方法还有载波移相正弦脉宽调制法,其在MMC中的应用研究已较为深入,但由于每个子模块的调制波必须由不同的PI调节器生成,控制难度将随着电平数的增加逐渐加大,同时可能因为电容电压平衡补偿时,参数选择不当而导致系统失稳[12]。相比较之下,CDPWM具有原理简单、方便拓展的优点,且通过VLM的方法可以很好地实现子模块电容电压的均衡控制[13]。
虚拟循环映射是在控制脉冲与SM之间引入虚拟子模块(virtual sub-modular,VSM),并通过改变VSM与SM间的映射关系,实现对调制信号的均衡控制。以五电平MMC为例,存在如图3所示的4种映射关系。

图3 VLM原理图Fig.3 Principle of VLM
同时,在CDPWM-VLM下,MMC子模块的等效开关频率fe将大大降低,其计算式为[14]
(1)
式中:fs为载波频率。该改进调制策略一定程度地减少了PWM调制方式下的高开关损耗,在MMC实际运行中有着重要的意义。
2 基于MMC-UPFC的谐波特性分析
在NLM方式下,MMC逆变输出电压的谐波分量主要为奇次谐波。通过Fourier分解,输出电压的解析表达式为
(2)
式中:UC表示子模块电容电压;ω表示基波角频率;θs表示第一个1/4周期内投入第s个电平时的电角度;smax为第一个1/4周期的电平阶跃数;N表示桥臂子模块数量,通常为偶数。考虑在m=1的正常工况下,则有
(3)
输出电压的谐波畸变率THD可以表示为
(4)
式中:Uh表示第h次谐波电压有效值;U1表示基波电压有效值。联立式(2)、(4),建立THD与N之间的关系式:

(5)
(6)
考虑61次谐波及以下,得出THD随N的变化曲线如图4所示。
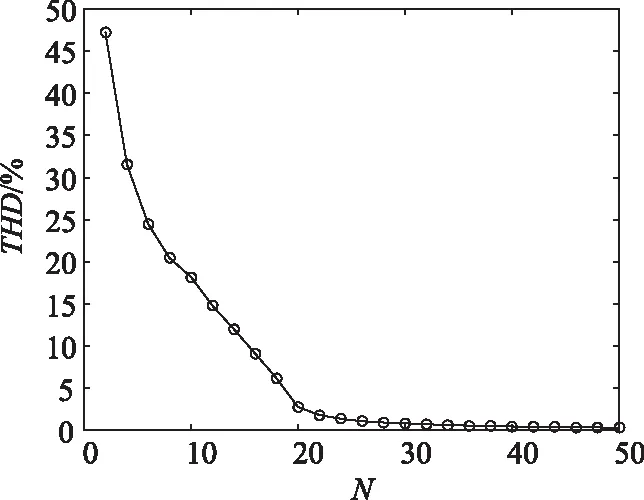
图4 NLM总谐波畸变率计算 Fig.4 THD calculation result of NLM
由理论计算结果可以得出,随着桥臂子模块数量的增加,MMC逆变输出交流电压谐波含量降低,当N≥20时,THD的降低幅度不再显著。
m=1时,MMC逆变输出交流电压电平数为N+1,其本质为一个相单元中子模块的N+1种投切状态。随着m的降低,一个周期内子模块的投切状态减少,为建立m与输出电平数的数学定量关系,引入等效子模块数Neq的概念,其对应的电平数为Neq+1。
Neq=|max(M-L)|
(7)
式中:M和L分别表示一个相单元中上、下桥臂投入的子模块数量,始终满足关系式M+L=N。
m的变化首先表现为子模块投切状态的变化,再表现为MMC逆变输出交流电压幅值的变化,即
(8)
式中:UacP表示MMC输出交流电压的幅值;Usm表示子模块电容电压。
由式(8)可得,m与Neq间的数学关系表达式:
(9)
结合式(6)可知,当N一定时,随着m的减小,等效子模块数减少,THD持续增大。
由上述谐波分析可以看出,在m较大时,MMC输出交流电压电平数足够多,NLM调制已经能够达到很好的输出特性,且开关损耗小;在m较小,输出电压电平数较少的情况下,NLM调制下电压谐波含量很高,且以低次谐波为主。相比较之下,CDPWM-VLM较好地改善了低调制比下输出电压的低次谐波,虽然引入了以载波频率为主的高次谐波分量,但便于滤除。
综上分析与考虑,本文提出一种基于NLM与CDPWM-VLM的混合调制策略,致力于改善低调制比下MMC输出串联补偿电压的谐波特性,在保证电压质量的同时尽可能减小器件开关损耗。
3 混合调制策略
3.1 混合调制策略的基本原理
混合调制策略是基于NLM调制方式与CDPWM-VLM调制方式的转换配合。在低调制比时采用CDPWM-VLM调制,高调制比时采用NLM调制,为提高调制方式切换控制器的抗干扰性,设置两个不同的高低阈值mH和mL,其切换过程存在两类情况,如图5所示。

图5 双阈值混合调制策略Fig.5 Hybrid modulation scheme with dual-threshold
在(a)类切换方式中,假设当前调制方式采用NLM,当m减小至mH时,调制策略将切换至CDPWM-VLM,若此刻m在(mL,1)区间内回升,控制器将始终采取CDPWM-VLM,同理,(0,mH)区间内,也会出现始终采取NLM调制的情况,不能体现混合调制策略的优势。(b)类切换方式则能有效避免这类问题,当m减小至mL时,调制方式由NLM切换至CDPWM-VLM,在回升过程中,当m>mH时,调制方式将切换回NLM。因此,本文所提的混合调制策略采用(b)类切换方式。
3.2 切换阈值的选取原则
混合调制策略切换阈值的选取包括两个方面,切换基准值mRef和双阈值切换的门限宽度Δm:
(10)
确定mRef与Δm之后,即可通过式(10)计算求得mH和mL。结合文章第二部分中对NLM调制方式下MMC逆变输出交流电压谐波特性的分析,通常认为,输出电平数达到9及以上,MMC逆变输出的阶梯波可以近似认为是正弦波[15],满足谐波要求。因此,要求等效子模块数达到8及以上,即
Neq=mRefN≥8
(11)
由式(11)可以确定mRef,再确定双阈值切换的门限宽度(mH-mL)。若门限宽度选取过小,控制器的抗干扰性将得不到太大的提升,过大则会带来不必要的开关损耗。定义门限宽度的最小分辨率Δd表现为桥臂中一个子模块的投切,则Neq的变化量为2,再结合式(9)即得
(12)
mH-mL=kΔd(k=1,2,…,N)
(13)
此外,考虑到在系统级控制目标指令值发生变化时可能产生一定的超调量,导致调制方式切换控制器对m的误判,因此,通过采集3个周期下串联补偿电压的平均调制比,提高调制方式切换控制器的准确性。双阈值混合调制策略的具体实现流程如图6所示。

图6 混合调制策略流程图Fig.6 Flow chart of hybrid modulation scheme
以南京西环网UPFC工程为例,桥臂子模块数量N=26,则可取mRef=8/26≈0.3;由于N较小,故取k=1,mH-mL=2/26。因此,可设置混合调制策略的双阈值为mH=0.34,mL=0.26。
4 系统仿真
在Simulink中搭建MMC-UPFC仿真模型,以南京西环网UPFC工程为参数依据,其中,并联侧换流器采用双环解耦控制策略,在调节并联侧与交流电网之间功率交换的同时,维持直流侧电压恒定。串联侧换流器采用交叉解耦控制策略,工作于潮流调节方式,通过串联侧注入电压实现对线路潮流的控制。表1为该UPFC工程主要参数。

表1 南京西环网MMC-UPFC工程主要参数
当采用混合调制策略时,两种调制方式间的切换首先应满足平滑切换,避免在切换过程中产生电压过冲现象,造成不利影响。其次,应满足尽可能快速地进行切换,使得混合调制策略能够更好地发挥其作用。
在搭建的MMC-UPFC仿真模型中,通过改变有功功率指令值,将系统的调制比由0.6降至0.24,低于切换阈值mL=0.26,调制方式将发生切换。如图7所示,其中,指令值于0.3s发生改变。由图7中MMC输出电压波形(以A相为例)可以看出,控制系统能够在3个周期内准确地对调制比的变化进行判断,并快速地切换调制方式。切换过程中,电压没有出现过冲现象。

图7 线路有功功率、串联侧MMC调制比及输出电压Fig.7 The active power of the transmission line and modulation ratio and voltage of series MMC
4.1 基于混合调制策略的谐波分析
选取当调制比从0.6降至0.4时的补偿电压波形图,分析当调制比发生改变(即0.3s)后的谐波特性,其中,图8(a)表示单一NLM调制方式下的谐波分布,图8(b)表示混合调制策略下的谐波分布。

图8 串联侧补偿电压谐波分布图Fig.8 Harmonics distribution of MMC voltage
可以看出,在低调制比下,补偿电压谐波含量已经达到一个较低的水平,电压波形的总畸变率由3.31%下降到0.16%。仿真结果验证了所提出的混合调制策略在改善谐波特性上的有效性。
4.2 谐波改善研究的方案对比
针对低调制比下的谐波改善问题,如引言中所提及,目前已提出的方法主要有直流降压法和特定谐波消去脉宽调制法。本节将对这两种方法展开更为具体的分析。
当直流侧电压为40kV时,UPFC并联侧工作在正常整流状态,且功率因数近似为1。并联MMC换流器交流侧电压Ush、电流Ish及直流电压Udc的波形如图9(a)所示。
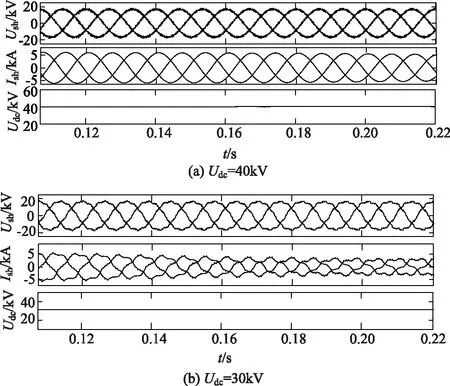
图9 并联MMC交流侧电压、电流及直流电压波形Fig.9 AC voltage and current wave of shunt MMC and DC voltage wave


图10 补偿电压谐波分布图(直流降压法)Fig.10 Harmonic distribution of MMC voltage
由上述理论分析和仿真结果验证可得,直流电压的降低导致了MMC整流侧交流系统性能的恶化,且在有限的调节范围下,直流降压法改善串联侧电压谐波的效果并不显著。
特定谐波消去脉宽调制法通过对逆变器输出电压进行傅里叶分解,利用基波和谐波的解析表达式设定相应的一组开关角,使得基波幅值跟随调制波且指定的谐波幅值为零。设在1/4周期内,一个电平下开关切换角个数为k,则可建立k个非线性方程,除去一个自由度用来控制基波幅值之外,可以消除(k-1)个频率的低次谐波。随着电平数的增加,开关切换角与非线性方程的个数近成倍增加。在MMC-UPFC应用场合中,当电压调制比发生变化时,其方程描述也将相应地变化,迭代求解过程需不断重复。已有研究指出,当电平数大于5时,该调制方法将变得十分复杂,适用性较差[16]。
针对MMC-UPFC谐波改善问题,列出3种方案的优缺点进行比较,如表2所示。

表2 3种谐波改善方案的对比
5 结 论
本文提出了一种适用于MMC-UPFC工程的混合调制策略,致力于改善串联侧补偿电压的谐波特性。混合调制策略以NLM与CDPWM-VLM调制技术为基础,充分结合二者优势。同时,为提高控制器的抗干扰能力,采用双阈值切换策略,并通过读取计算三周期下的平均调制比,在设定值处进行快速平滑的切换。结合南京西环网220kV MMC-UPFC工程进行算例仿真,并通过已有研究方案之间的对比,表明该混合调制策略能够使MMC-UPFC获得较大运行范围内的良好谐波特性,兼具有效性与可靠性。

