供给侧改革视域下中国省域能源效率及影响因素研究

刘浩旻，张在旭，王丽洋

（中国石油大学（华东）经济管理学院，山东 青岛 266580）

0 引言

“供给侧结构性改革”自2015年习近平总书记首次提出以来，指导各地区适度扩大总需求、不断提高供给体系质量和效率、寻求经济持续增长新动力。能源作为生产要素的必要投入，在人类社会和国民经济发展中具有重要的战略地位。推动能源结构优化升级，减少能源无效供给，合理配置能源资源，不断提高能源效率是能源供给侧结构性改革的目标。《中共中央关于制定国民经济和社会发展第十三个五年规划的建设》提出了“能源资源开发利用效率大幅的提高，能源消耗、碳排放量总量得到有效控制，主要污染排放总量大幅减少”的目标。中国经济进入“新常态”，改革进入攻坚克难的深水区，能源资源短缺，配置不合理，利用效率低下，随之产生的沙尘暴、雾霾等生态环境问题日趋严峻，可见提高能源效率，节约能源是中国实现经济转型升级和环境保护的必要条件。为此，本文对中国各省域能源效率及影响因素进行了研究，为能源供给侧结构性改革的实施和经济高质量发展提供理论依据。

1 研究方法

1.1DEA—BCC模型

数据包络分析（DEA）是Charnes和Cooper首次提出用于评价相同部门之间相对有效性的模型。本文选用DEA-BCC模型考虑非期望产出对中国省域能源效率进行测算。

假设决策单元有n个，每个决策单元都有m种类型的投入变量以及s种类型的产出变量，则有：

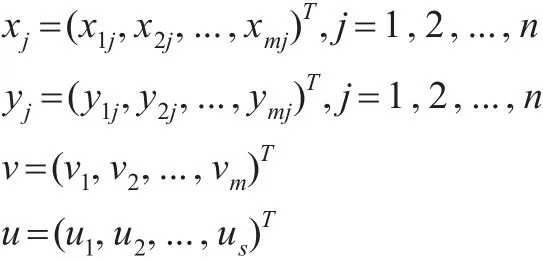
其中，xij表示第 j个决策单元对第i种输入的投入量，xij＞0；yrj表示第 j个决策单元对第r种输出的产数量，yrj＞0；νi表示第i种输入的一种度量（或称权重）；ur表示第r种输出的一种度量（或称权重）。

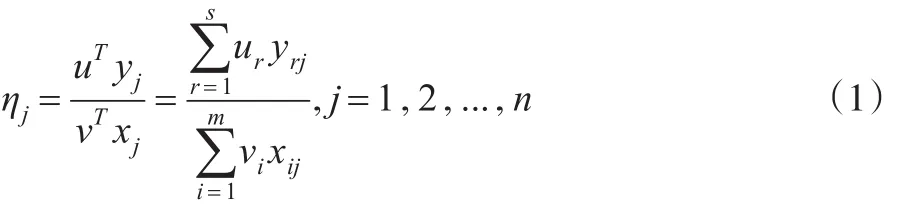
其实质确定一组最佳的权重变量 ν=(ν1，ν2，...，νm)T和u=(u1，u2，...，us)T。使得第 j个决策单元的效率值 ηj最大。

其中 ηj(j=1,2,…,n)均不超过1，即 maxηj≤1，若第j个决策单元ηj=1，说明该决策单元是有效的；若ηj＜1，表明该决策单元是无效的，其生产效率需要提高。

BCC模型是在规模报酬可变的条件下对效率进行测算，其表达式可以表示为：

其中，θ(θ≤1)的最大值为决策单元j0的技术效率值，λj为相对于决策单元j0重新构造的有效决策单元组合中第j个决策单元的组合比例，表示约束条件，与分别为m种投入变量和s种产出变量的松弛变量。

模型的含义为：①若θ=1且=0，=0，表明该决策单元有效，且其规模效应和技术效应同时达到有效，由其所组成的效率前沿面为规模收益不变；②若θ＜1且≠

0，≠0，表明该决策单元无效，决策单元的无效可能是由技术效率无效引起，也可能是由规模效率无效引起的，或者是两者的共同作用所引起的；③若决策单元是无效的，可以根据目标值对决策单元的投入和产出进行调整和改进，直至决策单元接近有效或者是完全有效。

1.2 面板数据模型

面板数据是一种二维结构数据，具有时间序列数据和截面数据的双重性质，既可研究对象个体间的差异又可研究个体随时间的变化趋势。面板数模型根据有无内生变量分为固定效应模型和随机效应模型，其一般形式：

其中，i=1，2，…N，表示横截面中研究的个体数目；t=1，2，…，T表示已知的T个时点；yit表示被解释变量单位个体i在t时的观测值；xkit表示的是第k个解释变量对单位个体i在t时的观测值；βki是模型中的待估计参数；uit是模型中的随机误差项。其矩阵形式为：

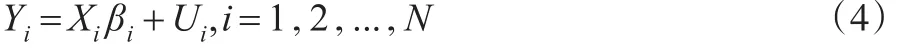
式（4）中：

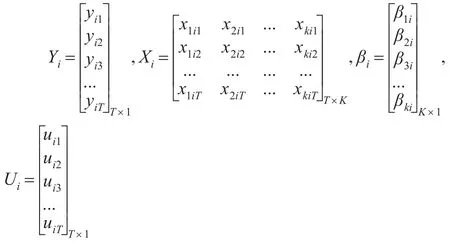
2 中国省域能源效率测算

2.1 指标选取与数据来源

根据中国各省市能源利用中对资本、劳动力、技术和环境的要求及国内外相关专家的研究成果，遵循科学性、可操作性和完备性的指标构建原则，构建能源测算指标体系，分为投入和产出两类指标，具体见表1。

表1 能源效率测算指标

2.1.1 投入指标

①劳动投入，用各省市劳动力质量的人力资本存量（万人）表示。计算如公式（5）所示：

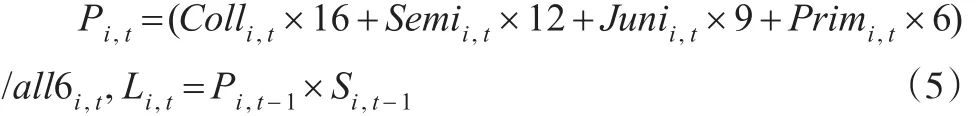
其中，Pi，t和all6i，t分别表示第i省第t年6岁及以上平均受教育程度和总人口，Primi，t、Junii，t、Semii，t、Colli，t分别表示第i省第t年小学、初中、高中、专科及专科以上的毕业人数，Li，t和Si，t分别表示第i省第t年人力资本存量和年末的劳动力总人数。相关数据均来自于历年中国统计年鉴。

②资本存量，用固定资本存量（亿元）衡量，由中国统计年鉴获得中国各省市历年固定资产投资完成额，采用单豪杰[16]的“永续盘存法”进行计算。计算如公式（6）所示：

其中，Ki，t、Di，t和Ii，t分别表示第i个省份在第t年的资本存量、固定资本折旧率和投资额度，Ki，t-1表示第i个省份在第t-1年固定资本存量。名义固定资本形成总额和固定资产投资价格指数均从中国统计年鉴和各省统计年鉴获取，固定资本折旧率借鉴单豪杰[16]采用的平均折旧率10.96%表示。本文的测算以2006年为基期，初始投资即为2006年的固定资本存量。初始资本存量的计算方法如公式（7）所示：

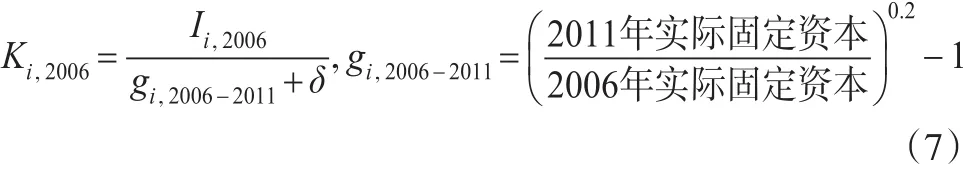
其中，Ki,2006、Ii,2006和gi，2006-2011分别表示i省以2006年为基期的资本存量、固定投资和固定资本的年平均增长率，采用平均增长率能够有效降低不同年份间资本差异过大所带来的误差。

③能源投入：将中国各省市生产和生活中煤炭、石油和天然气等能源的耗用统一折算成标准煤表示能源消费总量（万t标准煤）。相关数据均来自中国能源统计年鉴和各省统计年鉴。

2.1.2 产出指标

①期望产出，用各省实际生产总值（亿元）表示。为剔除价格变动产生的影响，确保历年数据间的可比性，本文以2006年为基期，将名义GDP换算为实际GDP。其中各省历年名义GDP和GDP平减指数取自中国统计年鉴。

②非期望产出，用环境污染产出综合指标表示。本文对废水排放量（万t）、酸性气体SO2排放量（万t）、氨氮排放量（t）和固体废弃物排放量（万t）四种污染物指标先进行标准化处理，再利用指标权重熵值法计算环境污染产出综合指标。四大污染物数据均来自中国和各省份历年统计年鉴。

熵值法的具体过程分为六步：

第一步：对原数据进行预处理，xij为某省份第i年第j个污染指标，计算公式如式（8）所示：

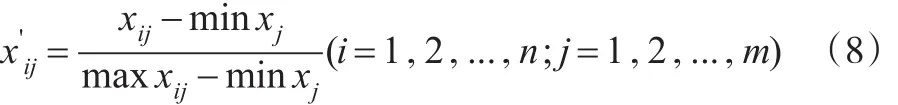
第二步：对预处理后的数据进行标准化，计算公式如式（9）所示：

第三步：确定第j个污染指标的熵值，计算公式如式（10）所示：

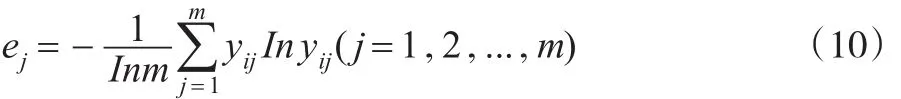
第四步：计算指标差异系数，差异性越小，表明指标对评价结果的影响越小，计算公式如（11）所示：

第五步：计算第j项污染指标的权重，计算公式如（12）所示：

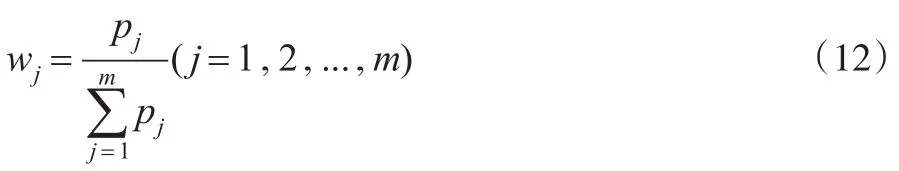
第六步：计算第i年环境污染指数，计算公式如（13）所示：

利用公式（13）计算2006—2016年各省市环境污染综合指标，值越低，能源效率相对越高。

2.2 能源效率的测算

采用DEAP2.1软件对各省市的能源利用效率进行测算。由测算结果（见表2）可知，各省市能源效率差异较大，以2016年为例，能源效率最高为北京市和上海市高达1.000，而最低值的青海市仅为0.314。样本期内，北京和上海的能源效率的效率值为1，均实现了能源效率最优。能源高质量发展要求产出过程中的非期望产出越少越好，北京上海一线城市的能源按需供给，且有效治理能源消耗中的污染物排放，注重生态保护，长期以来保持能源高效利用。天津、黑龙江、广西和广东四省的能源效率由1出现下降，天津和广西下降幅度过大，由效率值1分别降至0.443和0.373。天津和广西人口多资源少，石油、煤、天然气都常规能源均异常贫乏，经济的快速发展与能源有效供给的缺口越来越大，能源效率下降较多。其他24个省市呈现先上升后下降的波动状态。

3 中国省域能源效率影响因素实证分析

3.1 变量选择与数据来源

本文利用面板数据模型对能源效率影响因素进行实证分析，借鉴前人已有的研究，考虑数据的可得性，选取经济发展水平（ES）、技术进步（TP）、能源价格（EP）、城镇化水平（CL）、产业结构（IS）、能源消费水平（ST）、政府干预度（FR）8个因素作为解释变量，由BCC测算的能源效率值（EE）作为被解释变量，解释变量详见下页表3。

以上数据为2006—2016年的面板数据，解释变量相关数据来源《中国统计年鉴》《中国能源统计年鉴》和各省市统计年鉴，所有的变量数值都用比值或者绝对值的对数来进行表示。部分缺失值则通过相邻两年的平均值来进行弥补。

3.2 变量检验

3.2.1 变量描述性统计分析

相关变量的描述性统计如下页表4所示。

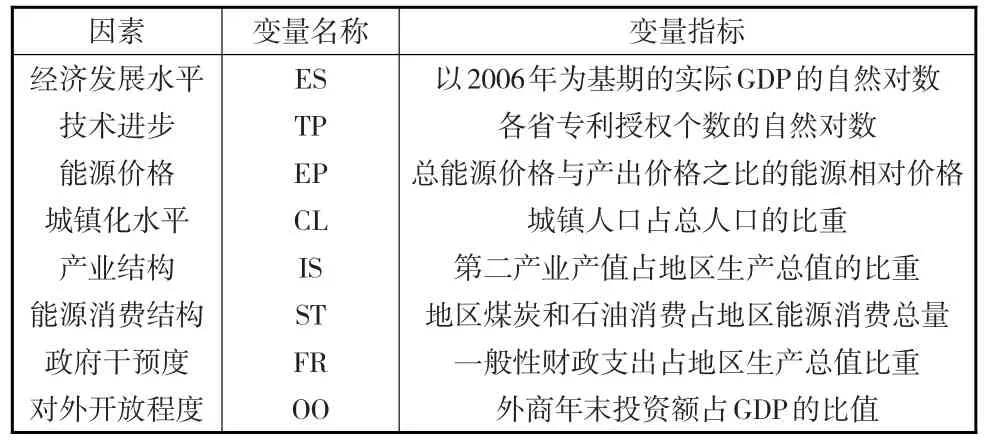
表3 解释变量指标

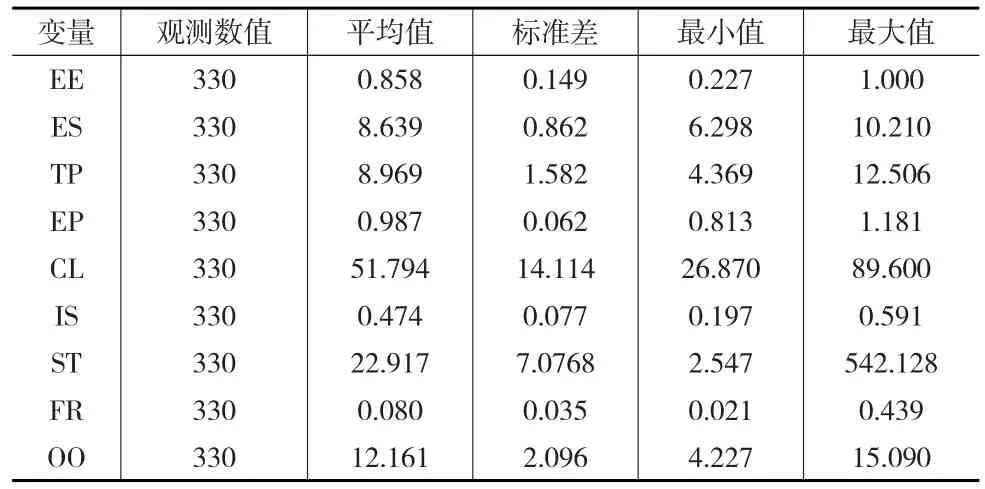
表4 面板模型相关变量描述统计

利用STATA12.0对变量进行描述性统计，从表4可以看出，每一个变量的330个观测值均没有出现极端数据，各数据的离散度较小。

3.2.2 多重共线性检验

进行回归分析时，必须保证解释变量间的独立性。若所选取的变量间存在相关性，将会影响模型估计的准确性和有效性。因此，本文通过STATA12.0软件采用膨胀因子法对解释变量的多重共线性进行检验。

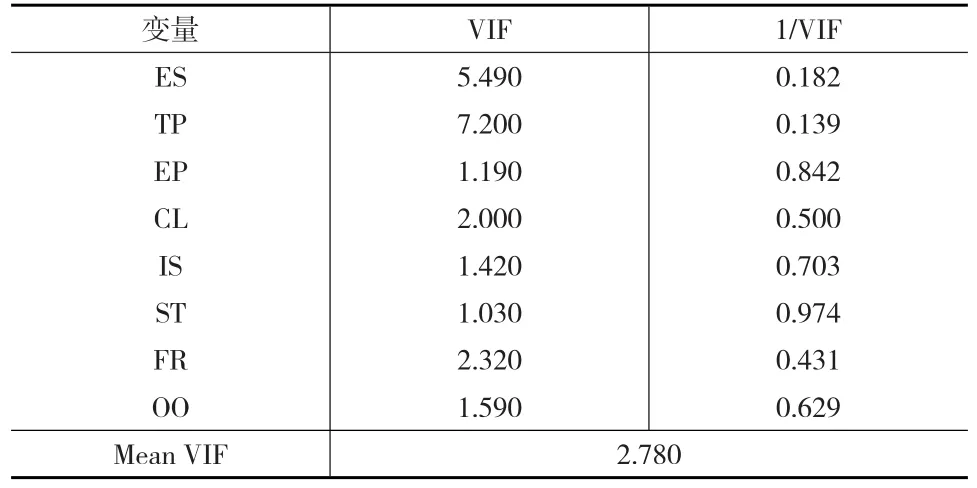
表5 相关变量多重共线性检验

如表5所示，模型中膨胀因子的平均值为2.789，与经验值2的差异较小，其最大值为7.200，远小于经验值10，故表明该模型不存在多重共线性。

3.3 结果分析

3.3.1 固定效应回归分析

对面板数据进行固定效应模型首次回归，结果显示：模型的拟合优度为0.7928，调整后的拟合优度为0.7962，F统计量为6.7900，回归方程成立。政府干预度（FR）的概率值为0.2300，对外开放程度（OO）的概率为0.3420，大于10%的显著性水平，表明这两个变量对我国省域能源效率的影响不显著。所以将FR和OO剔除再进行回归，回归结果如表6所示。

3.3.2 随机效应回归分析

对面板数据进行随机效应模型首次回归，结果显示：模型的拟合优度为0.6943，调整后的拟合优度为0.6362，F统计量为8.4500，回归方程成立。但政府干预度（FR）的概率值为0.1890，对外开放程度（OO）的概率为0.2620，大于10%的显著性水平，表明这两个变量对我国省域能源效率的影响不显著。所以将FR和OO剔除再进行回归，回归结果如表7所示。

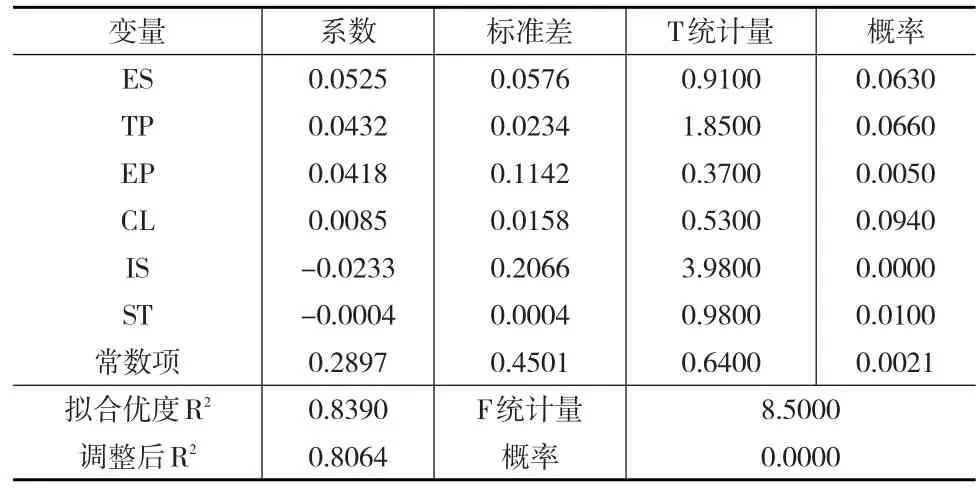
表6 面板数据固定效应回归

表7 面板数据随机效应回归

3.3.3 Hausman检验

对剔除变量的固定效应模型和随机效应模型进行Hausman检验，检验结果如表8所示。

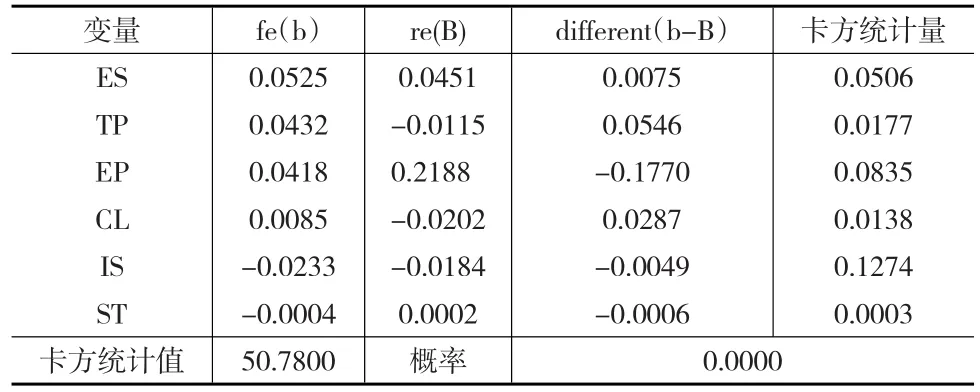
表8 回归模型Hausman检验

检验结果表明，模型卡方统计量为50.7800，接受原假设的概率为0.0000，因此在5%的显著性水平下拒绝原假设，应选固定效应模型及其估计方法研究中国各省域间能源效率的影响因素。回归方程见式（14）：

该结果表示了经济发展水平、技术进步、能源相对价格、城镇化水平、产业结构和能源消费结构对我国能源效率的影响方向和程度，通过固定效应检验结果可知，其先后通过了拟合优度检验和F检验，表明各个解释变量影响显著，所以回归模型成立。各个变量对能源效率产生的结果如下：

①经济水平（ES）与能源效率呈正相关关系。当其他的变量保持不变时，实际GDP的自然对数每提高1个单位值，能源效率平均上升0.0525个效率值。中国各省域GDP的提高有赖于能源消费，GDP越高，表明对能源的需求相对也就越高。需求的提高会反作用于供给，厂商将会扩大规模带动规模效率提高，进而促进整体效率的提升；

②技术进步（TP）与能源效率呈正向关系。保持其他变量不变，能源效率随各省域的专利授权个数的自然数每增加1个单位值而提高0.0432个效率单位。中国到2016年的专利授权数量达到175.38万件，比2015年增加了3.56万件。其中专利授权数平均数最多是广东省，最低的是青海省。相应的广东能源资源达到了最优配置，而青海能源效率仍需提高。虽然技术的进步不能仅仅用各省市的专利授权数来进行表示，却能够反映技术进步对于促进能源效率的提升至关重要；

③能源相对价格（EP）对能源效率产生积极影响。保证其他影响因素不变下，能源效率的平均值随能源相对价格提高1个单位而提高0.0418个效率单位。厂商购进生产要素的提高，带动其附属品燃料、动力类资源的价格的提升，成本的提升变相降低工业产品的价格，能源效率相对提高。能源相对价格的提高会使企业的利润降低，企业都是逐利的，为了保持自身效益和竞争优势，将会增加技术投入，在该产出水平下使投入的资源更少，从而提高了企业能源的利用效率；

④城镇化水平（CL）对能源效率有正向影响。各省份城镇人口所占比重每增加一个百分点，能源效率将相应提高0.0085个单位。北京和上海的城镇化水平较高，城镇人口占总人口的比重分别为86.5%和82.93%，而贵州的比重为较低的，仅为44.15%，但上海和北京的能源效率值远高于贵州。城镇化水平越高，引进的技术更先进，人才更优秀，同样投入在外部优越环境推动下产出更多，从而提高该地区的能源效率；

⑤产业结构（IS）与能源效率呈显著的负相关关系。第二产业比重每增加一个百分点能源效率下降0.0233个效率单位。2006—2016年，河南第二产业所占的比重最高，平均为54.61%，第二产业所占比重最低的是北京市，仅为23.77%，而北京的能源效率远高于河南。河南作为中国人口大省，中部崛起战略的实施有效推动第二产业发展，对能源的需求远高于北京市；第二产业所占比重对能源效率有消极影响，相比北京，河南第二产业处于规模报酬递减阶段，生产资料的配置已超过最佳组合，使得该产业能源效率下降，而影响整个省的能源效率；

⑥能源消费结构（ST）对能源效率产生消极影响。当其他影响因素不变，煤炭、石油消费比重每上升1个百分点，能源效率随之下降0.0004个效率单位。西北地区煤炭石油在能源消费比重偏高，沿海地区的电力消费比重偏高，调整每个地区的煤炭、石油、电力消费比例，会相应的调整各种能源利用的贡献度，有利于提高各个地区的能源效率，从而提高中国整体能源效率。

4 结论

本文在考虑环境非期望产出基础上利用DEA-BCC模型和面板数据模型对2006—2016年中国各省域能源效率及影响因素进行了分析，结果显示：①样本中，同一年份不同省市之间能源效率差异较大，北京市和上海市能源效率值高达1，而最低值青海市仅为0.314；②样本期内，中国能源效率总体上呈现先上升后下降趋势；③地区经济发展水平、科学技术发展水平、能源相对价格变化、地区城镇化水平与能源效率呈显著正相关关系；④第二产业所占的比重、煤炭石油为主的能源消费结构与能源效率呈负相关关系；⑤在能源效率影响因素上，政府干预程度和地区对外开放程度对中国省域能源效率影响不显著；因此，政府应考虑各区域实际情况，因地制宜制定与能源供给侧结构性改革相适应的对策，提高整体能源效率。