常微分方程两步估计的方差估计

卫泽林，赵 恒

（西安电子科技大学a.数学与统计学院；b.通信工程学院，西安 710126）

0 引言

常微分方程理论在很多领域都有广泛的应用，通过分析系统所建立的常微分方程模型，可以对客观过程提供一个很好的描述。常微分方程的应用性通常依赖于某些参数，了解这些参数对研究常微分方程刻画的动力系统是至关重要的，然而这些参数在实践中往往是未知的，它们必须从带有噪声的观测数据中推断或估计出来[1-3]。

最小二乘估计具备良好的特性，因此在实际研究中有很大的作用，但是当方程为一个非线性的高维系统的时候，最小二乘估计就会有很大的局限性。这种情况下，需要在非线性高维的参数空间下找到使得函数达到最小的值，其解决过程通常是通过梯度的算法完成的。虽然这些算法的改进对参数估计有了很好的结果，但是在实际的应用中，仍需要很大的计算量才可以完成，这样就会影响在实际应用中的效率。为了避免以上两种算法的困难，提出了两步估计法[4，5]，该方法的第一步只需要用核光滑估计[6]找出相对应的非参数估计，因此很大程度上节省了计算时间；第二步最小化方程残差平方和就可以得到参数的估计值。

同时，参数的方差估计是一个很重要的指标。如果方差估计不可知，则难以进行很多其他的统计推断，比如假设检验和区间估计等。但是针对两步估计的方差估计没有理论的结果。本文通过对一个三维的Lotka-Volterra种间竞争模型[7]用两步估计进行参数估计，针对估计出来的参数用boostrap方法做方差估计。

1 两步估计基础知识

考虑下面的常微分方程系统[8]：

其中X(t)=(X1(t)，…，Xm(t))T∈Rm是m维的状态变量，θ=(θ1，…，θd)T∈Θ，Θ∈Rd表示的是d维的未知参数，Ẋ(t)是X(t)的导函数。

假设对第i个状态变量Xi，在时间tj时的观测样本点为：

其中εij是服从独立分布的模型随机误差，且满足Eεij=0和 Var(ε)=σ2。

第一步：X(t)和Ẋ(t)的估计可以通过非线性方法，例如核光滑，样条函数[9]等实现，本文中利用核光滑[10]来估计。

Rosenblatt于1955年提出：对每个点x，Δx表示以x为中心，长为h的区间，即[x-h/2，x+h/2] 。以x1，...，xn落入 Δx的个数除以nh，即{j:xj∈Δx，j=1，...，n}/nh作为x密度函数f(x)的估计。由此看出Rosenblatt方法与传统直方图方法的区别在于：分割区间随着要估计的点x变化，x始终位于区间的中心位置，从而能够获得较好的效果。

引入函数：

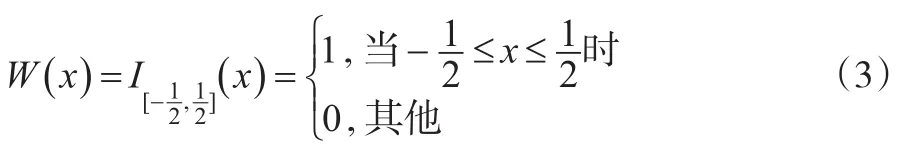
则上述f(x)的估计可表示为：

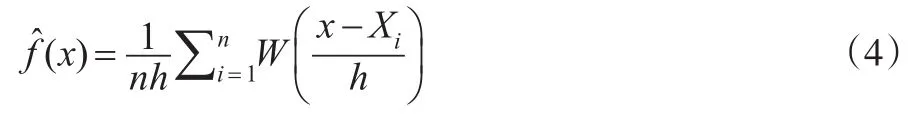
从Rosenblatt估计看出，由于W(x)是均匀分布，为估计f在点x的取值f(x)，与x距离h2以外的样本点不起作用，而在距离h2以内的样本点作用相同。考虑到用整个样本x1，...，xn估计f(x)，直观上，越接近x的样本点对f(x)的估计影响应当越大。Parzen于1962年把Rosenblatt估计推广为核光滑估计：

如果K()

μ是一个给定的概率密度，则f(x)的核估计为：

其中K(μ)称为核函数，h为窗宽。

可以根据以上核估计函数估计出X(t)和Ẋ(t)，记光滑后的为X(t)和Ẋ(t)分别为a(t)和b(t)。

第二步：估计参数θ的值。通过解下面的优化问题就可以得到参数θ的估计值：

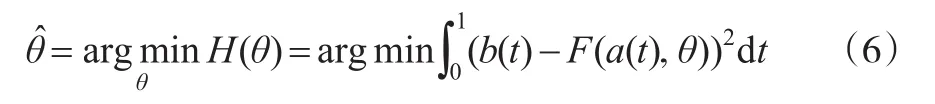
其中H(θ)=(b(t)-F(a(t)，θ))2dt。

2 Lotka-Volterra模型的两步估计

Logistic方程始于上世纪上半叶做昆虫养殖实验提出的“虫口方程”，同一时代即在人口研究、鱼群捕捞研究乃至生态系统研究上迅速发展起了Logistic方程的理论与应用研究，至今方兴未艾。Logistic方程起源于生物领域的研究，但该方程可以说是提出了描述一切客观系统发展过程的一个最简单、最基本、最广泛且最有用的数学模型。由于一维的Logistic方程仅限于描述单个事物或系统的发展过程，为了描述种群间的竞争关系Lotka和Volterra早在20世纪20年代，对一维Logistic方程进行直接扩展，提出了种群间竞争模型[11]。

考虑以下三维的Lotka-Volterra（LV）种间竞争模型：

将光滑过后的X(t)和Ẋ(t)分别记为：

未知参数：

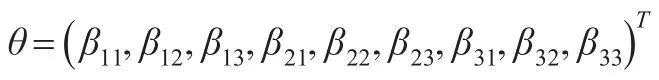
以第一个方程为例，记参数θ1=(β11，β12，β13)T的系数为h1(t)=(X1(1-X1/K)，X1X2，X1X3)，取K=1，则求解以下优化问题就可以得到θ1的估计：

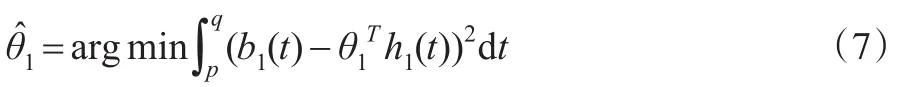
对上式求导并令其为0，可解得最优解为：

类似的可以估计出其余两个方程中的参数。

在做实验时，利用模拟数据，设定参数为：

θ=(0 .01，0.01，0.01，0.02，0.02，-0.02，0.01，0.02，0.03)T，该值可以作为参数评价的一个标准。利用模拟数据做100次实验，试验中三个变量的噪声均满足正态分布N(0.0.022)。

表1 Lotka-Volterra模型中参数的估计结果

从表1中整体来看，各个参数的估计值都比较准确，多次实验后求得的参数估计的均值也比较准确，ARE较小。图1至图3中，x1、x2和x3分别是状态变量的标准值，x11、x22和x33分别是将估计出来的参数代入方程，再用龙格库塔解出的状态变量的值，两者相比较，从图中可以看出，两步估计效果很好。

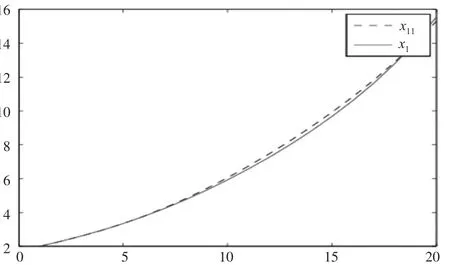
图1 标准的x1和其估计值的x11的对比

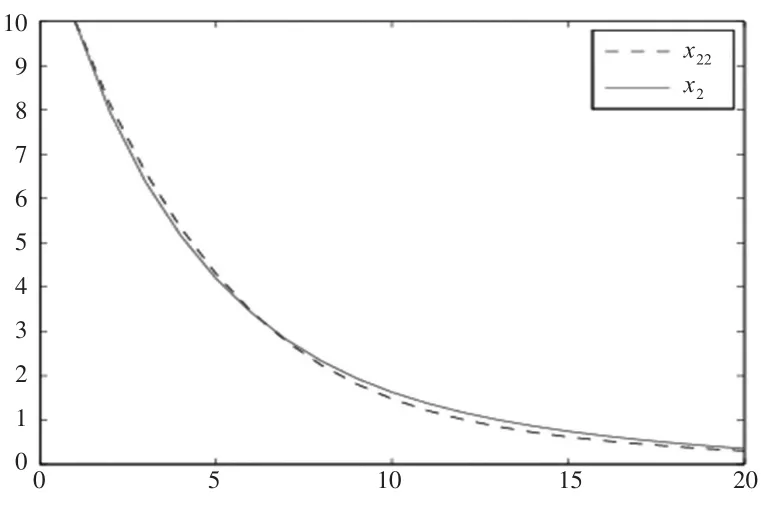
图2 标准的x2和其估计值的x22的对比

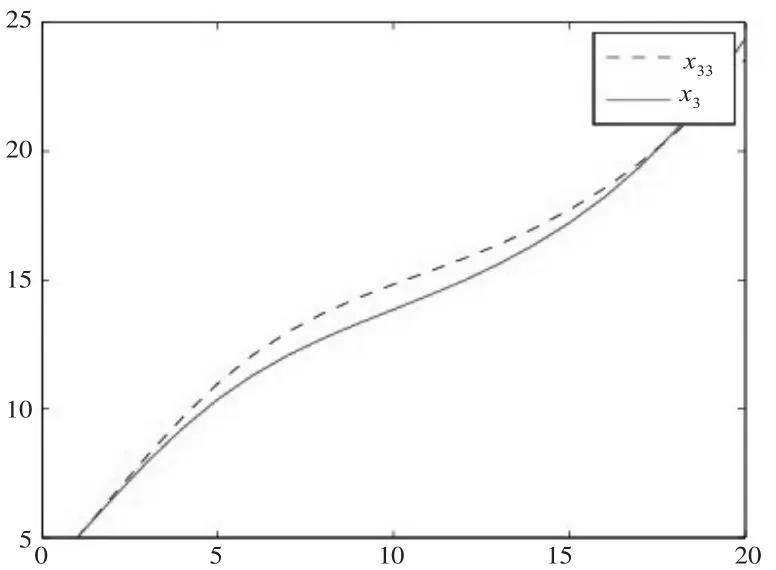
图3 标准的x3和其估计值的x33的对比

但是在第一步估计中，用光滑的核函数估计X(t)时，其中需要选择合适的窗宽，不同的窗宽对参数估计的结果影响较大，因此表1的估计结果不一定是最优的，下文将介绍该模型中最优窗宽的选择。

3 核光滑时窗宽的选择

在核光滑估计问题中，窗宽的选择[12]直接影响到估计的好坏，而核函数形式对估计的影响甚微。窗宽h越大，则光滑越好,但可能忽视有用信息，而拟合不好。反之，h越小，则拟合较好，但可能光滑不够，无法把有用信息和干扰分开。

窗宽参数的选择有许多种方法，通常第一步的核光滑估计可以采用数据驱动的交叉验证或者建立在渐近平均整合平方误差基础上的替换法，其最优窗宽为：

Liang和Wu[13]在2008年提出另一种两步估计的最优窗宽为：

其中an是一个收敛于0但收敛速度慢于log-1n的序列，在本文他们选择an=log-1/16n。

本文使用Lotka-Volterra模型来进行实验，模型中观测时间为1～20天，则n=20，由于 log20＞1，因此an＜1，那么在这个模型中有：

本文分别取an1=log-1/106n，an2=log-1/16n，an3=log-1/6n，对应窗宽分别为hn1=0.4244，hn2=0.3967，hn3=0.3538，每个窗宽下做100次实验，求估计参数的均值，选择该模型下的最优窗宽。

表2 Lotka-Volterra模型中不同窗宽下估计参数的ARE

由表2可以看出，无论哪个参数，其变化规律和结果都是一样的：

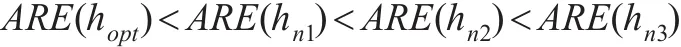
其结果可以看出，对于Lotka-Volterra模型，窗宽的选择使用hopt=n-1/5时，估计的参数更加准确，而若使用公式hn=n-2/7an,当观测值个数一定时，窗宽会受到限制，只能取到一定小范围内的值，而不一定可以取到最优窗宽，从以上模型的实验来看，使用hn=n-2/7an公式时，在可取得的窗宽范围内，窗宽越大，ARE越小，估计越准确。

4 用boostrap法估计两步估计的方差

本文用Lotka-Volterra模型做实验时都用的模拟数据，因此可以模拟多组实验数据以计算方差，但是在实际问题中通常只会有一组数据，也只能根据这一组数据估计参数，难以计算方差。Boostrap是现代统计学较为流行的一种统计方法，在小样本时效果很好[14，15]。通过方差的估计可以构造置信区间等，其运用范围得到进一步延伸。所以本文使用boostrap估计两步估计参数的方差。

这种方法的过程比较简洁：

（1）首先采用重抽样技术从原始样本中抽取一定数量的样本，这个过程可以重复。而在两步估计中，目标是解决:

这是一个积分问题，可以从积分区间入手，将积分区间[a，b]均匀的等分为N份，看成N个原始样本，从中可放回的抽取N个样本区间。

（2）根据抽出的样本区间计算常微分方程中的参数的估计值：

（3）重复上述过程n次，得到参数的n个估计值。

（4）最后计算上述参数n个估计值的样本方差，这样就得到了常微分方程估计参数的方差估计。

下面本文将这种方法运用在Lotka-Volterra模型中，用20个观测值做实验，试验中第一步估计的窗宽选择第3部分中得到的最优窗宽值hopt=n-1/5。用上述方法计算可以估计出来参数的方差。而由于实验中是模拟数据，因此也可以计算出其标准方差，由于方差数值较小，比较不方便，而用标准差比较性质也不会发生改变，因此表3中使用标准差比较实验结果。

表3 boostrap法做两步估计的方差估计

表3中，第二列是由多次实验计算得到两步估计的参数估计值，再计算这些参数估计值标准的方差，进而求出标准差，第三列是由用boostrap方法取样，估计方差并求出标准差。可以看出，用boostrap做常微分方程参数方差估计的方法计算出的方差与标准方差相比相对误差较小，这种方法做方差估计较精确可行。

5 总结

常微分方程模型在很多领域中都有广泛的应用，比如生物学和医学等。而常微分方程中参数的估计方法也多种多样。本文利用基于光滑的核函数两步估计法来估计参数，这种方法比传统的参数估计方法更简洁有效，计算效率高。其次本文研究了两步估计中窗宽对估计参数方差的影响。最后基于最优窗宽，提出了用boostrap法做两步估计的方差估计。本文通过对一个三维的Lotka-Volterra种间竞争模型进行参数估计，针对估计出来的参数做方差估计，并验证了该方法的有效性。方差的估计对很多统计推断问题很有意义，例如假设检验，区间估计等，本文研究了两步估计的方差估计，但是由于两步估计本身的一些性质，其中很多因素都会对估计结果造成影响，因此很难将所有影响因素考虑进去，进而找到一个最优的方差估计。这些需要在未来的工作中继续研究。其次本文提到的方法在高维常微分方程上的推广也有待进一步研究。