一种自适应的RFID防碰撞算法

任柏翰，张圣杰，石浩森，宫 婧

(南京邮电大学，江苏 南京 210023)

0 引 言

射频识别(radio frequency identification，RFID)技术可以通过无线电讯号实现无接触式自动识别，由于其具有阅读速度快，可适应于各种恶劣环境，读写能力快等优点，现已广泛应用于交通物流、食品管理、图书馆书刊借阅、门禁等各个领域[1]。但当多个标签同时与读写器进行信息传输时，会出现“碰撞”现象，使阅读器无法正常工作，严重影响系统正常运行。为解决这一问题，现已提出了多种RFID防碰撞的算法[2]。

1 当前防碰撞算法

常用的防碰撞算法一般可以分为两类：确定算法和非确定算法[3]。非确定算法主要是基于ALOHA算法，包括时隙ALHOA算法、分群时隙ALOHA算法等。确定性算法主要是基于二进制树搜索的算法，包括二叉树搜索算法、动态二叉树搜索算法、自适应树搜索算法等[4]。

纯ALOHA算法[5]就是当需要发送数据时，标签以循环序列形式发送数据，在第一次发送之后，需要等待相对较长的时间再次发送数据，直到所有标签都完成了数据的发送。时隙ALOHA算法[6]把时间以帧为单位分成时间段，每个时间段由若干个时隙组成，标签发送数据帧只能在时隙开始时发送，按照这种方法，可以大大减少因为帧重复引起的冲突。

二叉树搜索[7]的基本思想是将处于冲突的标签分成左右两个子集0和1，先查询子集0，若没有冲突，则正确识别标签结束。若仍有冲突则再继续分裂，把子集0分成00和01两个子集，依次类推，直到识别出子集0中所有标签，再按此步骤查询子集1。

四叉树搜索的基本思想是将处于冲突的标签分成四个子集00、01、10和11，先查询子集00，若没有冲突，则正确识别标签结束。若仍有冲突则再继续分裂，依次类推，直到识别出子集00中所有标签，再按此步骤依次查询子集01、10、11。

2 改进防碰撞算法

ALOHA算法当标签达到一定数量的时候，容易发生某些标签多次碰撞无法识别的状况，也就是“标签饥饿”现象[8]。二进制树形转化法则不存在这一现象。目前已经存在的算法有动态二叉树搜索算法、动态的四叉树搜索算法、自适应的二四叉树防碰撞算法[9]。

二叉树搜索时，不存在空闲时隙，但是碰撞时隙的数量非常多；四叉树搜索时，可大幅度减少碰撞时隙，不过增加了空闲时隙的数量。自适应的二四叉树，引入碰撞因子的概念，根据当前集合碰撞因子的大小，自适应地选择采用搜索树的类型，从而大幅提高效率。

不过之前的文章由于考虑到引入八叉树系统设计算法更加复杂，因此没有对八叉树进行进一步的分析，而是仅分析二四叉树。当标签数目较多时，为进一步优化算法，文中提出一种自适应的二四八叉树算法，以进一步优化标签碰撞识别过程。

动态八四二叉树搜索流程如图1所示。

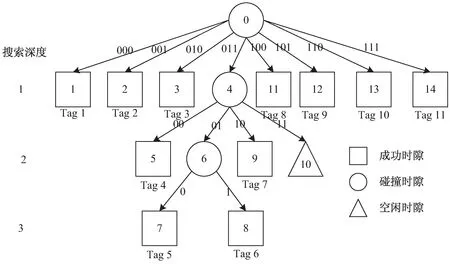
图1 动态八-四-二叉树搜索流程

通常来讲，当系统内的标签数量越多，则出现碰撞的位数也就越多，从而碰撞位占标签总比特位的比例也就越大。为了更好地决定采用几叉树进行搜索，定义了碰撞因子μ来计算这个比例，以便有效地利用碰撞信息，提高算法效率。

定义：假设每个标签的ID码长度为n比特，其中碰撞间隙内产生碰撞的比特位为nc，则

(1)

其中，碰撞因子μ包含了待识别的标签的数量的信息。

假设系统内有M个待识别的标签，每个标签的ID码长度为n比特，其中任意一位不发生碰撞的概率为(1/2)M-1,由此可得：

(2)

式2表明，系统中标签的个数越大，碰撞因子值越高；反之，碰撞因子值越低。由此说明碰撞因子的大小可以用来估计待识别标签的数量。

在文献[10]中给出了计算碰撞因子值的方法，即碰撞因子与叉树的关系。假设系统内有M个待识别的标签，自适应多叉树的叉数为L，当搜索的深度为1时，标签的识别概率为P(1)=(1-1/L)M-1；当搜索深度为2时，识别概率为P(2)=P(1)[1-P(1)]；以此类推，当搜索的深度为k时，得到标签的识别概率为P(k)=P(1)[1-P(1)]k-1。

所以，需要搜索的深度均值为：

(3)

所需的平均时隙为：

(4)

根据计算可知，当L=M时，所需的平均时隙最少。理论上来讲，待识别的标签越多，多叉树的叉数越多，但实际上只考虑二叉树、四叉树和八叉树。

通过比较得知：当M<3时，T为T2；当3≤M≤5时，T为T4；当M>5,时，T为T8。其中，M=3为二叉树和四叉树的临界值，此时计算得μ=0.75；M=5为四叉树和八叉树的临界值，此时μ=0.937 5。因此得出，当μ<0.75时，选择使用二叉树搜索；当0.75≤μ≤0.937 5时，选择四叉树搜索；当μ>0.937 5时，选择使用八叉树搜索。

EIAMS算法流程如图2所示。

Step1：读写器初始化查询堆栈，发出查询命令。

Step2：与阅读器前缀相符合的标签响应。

Step3：若标签响应数为1，识别成功，为成功时隙；若无标签响应，识别失败，为失败时隙；若有多个标签响应，则进入碰撞时隙。

Step4：碰撞时隙：计算碰撞因子μ，若μ>0.937 5,采用八叉树，根据碰撞首位，重新确立八个查询代码，并进入栈记录；若0.75<μ<0.937 5,则采用四叉树，根据碰撞首位，重新确立四个标签查询，并进入栈记录；若μ<0.75，则采用四叉树，根据碰撞首位，重新确立八个标签查询，并进入栈记录。

Step5：判断栈，如果栈空，则结束，如果不为空，跳转到Step2。

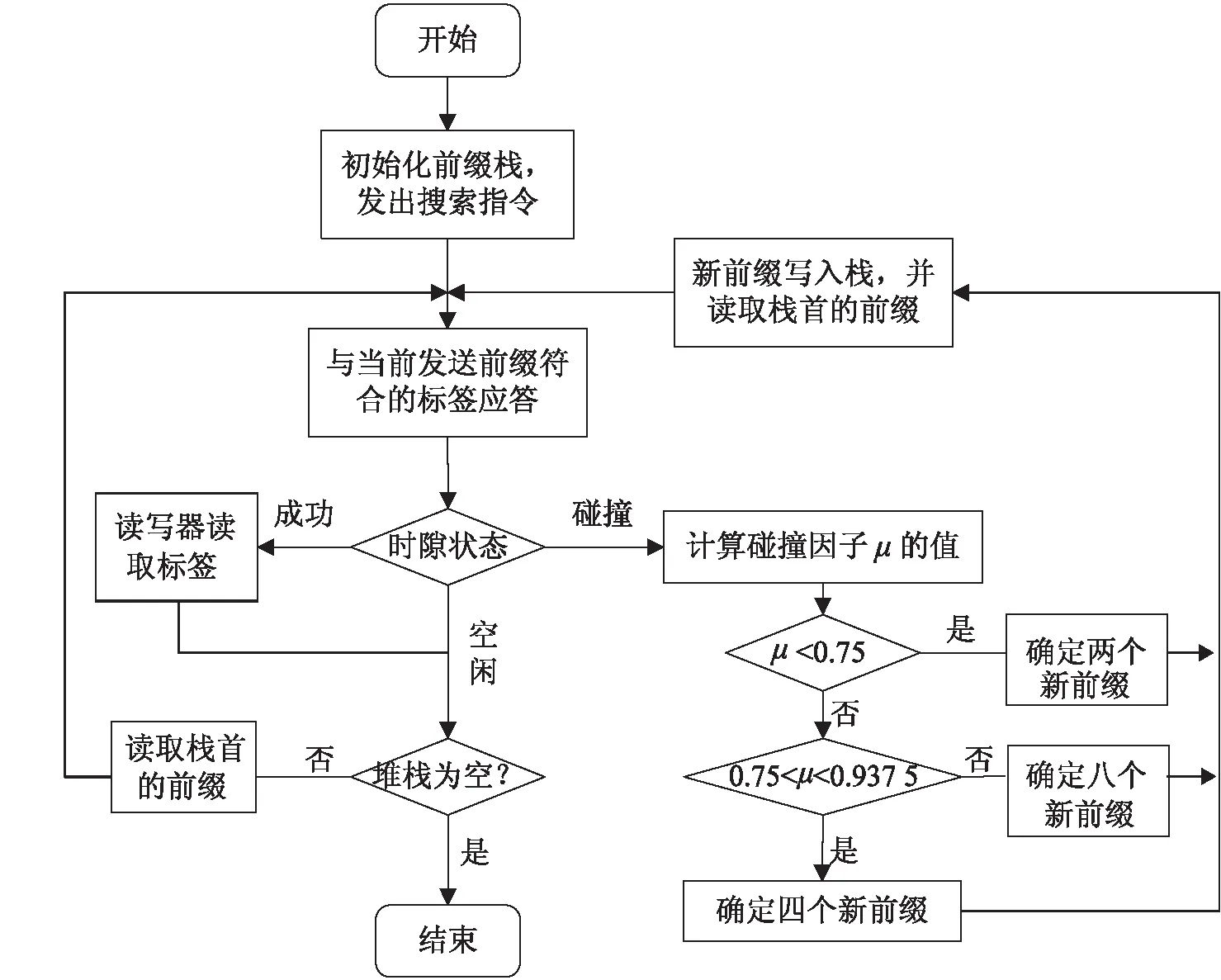
图2 EIAMS算法流程

3 算法性能分析

标签在识别过程中的时隙总数即为时间复杂度。假设待识别的标签数为n，在纯二叉树搜索算法中，总时隙数为2n-1[11];在纯四叉树搜索时，有如下推导的过程：

在纯四叉树中，叶子节点的度为0，记叶子节点个数为n0；其他节点的度为4，记其他节点的个数为n4；此总节点数为N,有：

N=n0+n4

(5)

除根节点，其他所有节点都有一个根，考虑根的个数为：

N=0×n0+4×n4+1

(6)

联立式1和式2可得：

n0=3×n4+1

(7)

由于n0=n+nk，nk为空闲时隙，因此

n+nk=3×n4+1

(8)

对于一个发生碰撞的时隙，其空闲时隙最大数量为2，最小数量为0。

当一个碰撞产生2个空闲时隙时，nk=2×n4，代入式8可得n=n4+1，时隙总数为N=n+nk+n4=4n-3；当一个碰撞不产生空闲时隙时，nk=0，代入式8可得n=3×n4+1，时隙总数N=n+n4=(4n-1)/3。

因此，在纯四叉树中识别的时隙总数取值范围为：[(4n-1)/3,4n-3]。

同理可得，在纯八叉树中识别的时隙总数取值范围为：[(8n-1)/7,8n-7][12]。

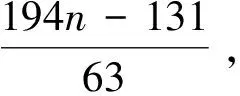
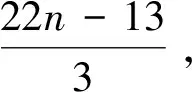
由此可见，改进后的算法与之前的算法相比，在时间复杂度上没有量的提高，在识别的时隙总数上有较为明显的减少。因此，改进算法近一步优化了RFID防碰撞算法。

在实际应用中，由于二叉树、四叉树、八叉树在搜索流程中所占比例不同，因此在总时隙处理上不能简单地进行平均，而是应该进行加权平均。采用平均方法与实际状况尽管会存在一定差距，不过在总体趋势上，基本是相同的。

4 实验仿真分析

根据上面的算法描述，采用MATLAB_R2017a对改进算法与之前常见的二叉树、四叉树、二四叉树等算法进行仿真对比分析。

仿真过程中，四种算法统一采用随机生成的16位RFID标签。对不同算法在标签总数从10到300以步长为10变化，每种算法重复进行1 000次进行仿真，记录下参数后最后取平均值。图3为四种算法所需要的总时隙数、吞吐率的比较。

图3 总时隙数变化仿真图

为了更好地衡量算法的优化程度，定义算法提升度的概念，根据时隙多少来衡量算法的优化程度，算法提升度公式为：

(9)

将二-四叉树算法与二四八叉树算法选择部分标签数量，列出算法提升度表格，如表1所示。

根据上述实验仿真结果可知，从总时隙上看，当标签在数量较少时，二四八叉树算法明显优于二四叉树；而当大于100时，二四八叉树却不如二四叉树，不过两种算法相差依然较小。根据算法提升度表格可以看出，随着标签数量的提高，与二四叉树相比改进后的算法提升度在降低。因此，改进后的算法更加适用于中小型系统[13]。

表1 算法提升度

吞吐率变化仿真如图4所示。

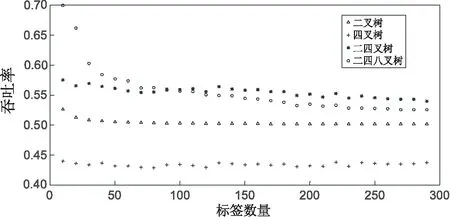
图4 吞吐率变化仿真图

从吞吐率看，当标签在100之内时，二四八叉树显然优于二四叉树，当标签大于100时，二四叉树优于二四八叉树。不过对比单一的二叉树和四叉树，二四八叉树无论在总时隙还是吞吐率上，都有明显的优化。

可见，在标签数目比较多，即碰撞率高时，引入八叉树反而会减弱算法。以4位标签为例，分析树形即可发现原因。当采用二四八叉树时，树第一层为八叉树，将前3位标签分开，由于标签长度总为偶数，这时必定会有1层需要用二叉树；如果采用二四叉树，第一层对应前两位，第二层对应后两位，总时隙数比改进后的算法反而要优化。

5 结 论

为解决射频识别过程中多个标签同时存在引发的碰撞问题，在自适应二四叉树防碰撞算法的基础上，将八叉树引入，提出了一种改进的自适应的二四八叉树算法。算法通过计算标签的碰撞因子，自适应地选择最优树的叉树，然后进行搜索，从而大大减少了空闲时隙。对改进算法进行复杂度分析后，发现改进算法的复杂度与标签数量近似呈线性关系。

针对不同标签数量的搜索过程，在总时隙数和吞吐率两个方面对算法进行仿真。结果表明：当标签数目较少时，采用二四八叉树相结合的算法优化效果十分明显，可以大幅度提高系统吞吐率；不过当标签数目较多时，二四八叉树在总时隙数上不如二四叉树。与单纯的二叉树或者四叉树相比，不论总时隙数多少，改进后算法都具有明显的提高。

在实际应用中，如果标签长度为奇数，或者标签中有奇数位数未使用，读卡器不需要识别。这时候采用二四八叉树将会有较优的结果。

6 结束语

提出了一种改进的自适应的二四八叉树算法，根据碰撞因子自适应选择搜索树的叉数，仿真结果表明，在标签一定的数量内，算法大幅度减少了总时隙，提高了吞吐率，不过超过一定数量算法性能会降低，适用于小型的射频识别系统。目前，算法仅仅研究了基于多叉树二进制防碰撞算法，今后可以在此基础上，着重研究多种防碰撞算法的混合使用。