具有学习效应和退化效应的单机排序问题
罗成新, 李 石
(沈阳师范大学 数学与系统科学学院, 沈阳 110034)
排序理论是组合最优化学科的重要组成部分之一,具有非常重要的理论意义,广泛应用于各个学科之中。大型复杂工作排序的好坏对工程费用大小影响很大。在传统调度模型之下,大多数假定任务的加工时间是一个给定的常数值,但随着科学技术的迅速发展,人们发现这种假设并不能更好地贴近实际生活。影响工件加工时间的原因多种多样,如因机器老化而造成的退化效应,或因工人反复操作提高技术而产生的学习效应,或资源分配等情况,任务的加工时间不再是固定不变的。Liu等[1]研究了带有学习效应且加工时间依赖于资源分配的最优交货期排序问题,目标是通过获得最优交货期位置和最优排序使目标值最小;王吉波等[2]研究了同时具有学习和恶化效应的不同工期的指派问题;文献[3-4]相继研究了同时具有学习效应和退化效应的单机调度问题。近年来带有交货期窗口的问题逐渐走进了人们的视野,相比于交货期问题[5-7],更加贴近实际生产的需要。Sidney[8]首先提出了带有交货期窗口指派的单机排序问题,目标是找到工件的最优排序及提前、误工的最小费用。此类问题中规定若一个工件在交货期窗口起始时间之前完成,则需要承担一部分提前惩罚费用;若一个工件在交货期结束之后完工,则需要接受一部分延误惩罚费用[9-11]。
此外,带有资源分配的问题也逐渐得到了人们的关注。Wang等[12]研究了带有截断控制参数学习效应、退化效应、资源分配的单机调度问题;Ji等[13]研究了带有公共交货期窗口且带有资源分配、退化效应和维修活动的单机排序问题。本文在上述2篇论文的基础上,假定所有工件有一个公共交货期窗口,研究同时具有截断控制参数学习效应和退化效应且工件加工时间依赖于凸资源分配的单机调度问题。进一步推广了目标函数,通过确定最优交货期窗口位置以及规模、最优资源分配方案及最优排序,求出目标函数最优值。分2种情况:限制资源总费用的前提下,使提前、延误、工期窗口开始时间、工期窗口大小、绝对完工差异、总完工时间和、总资源费用最小;限制带有提前、延误等费用,极小化总资源量,证明所研究的2种问题是多项式时间可解的,并给出2个最优算法。
1 问题描述
研究下面问题:有一台机器,设n个独立工件N={J1,J2,…,Jn}需在这台机器上连续加工,即加工期间不允许中断。其中,一台机器同一时间最多只能加工一个工件,全部工件在0时刻到达并且为可用状态。本文中,考虑带有截断控制参数的学习效应和退化效应的凸资源分配模型,设工件Jj的实际加工时间表达式为
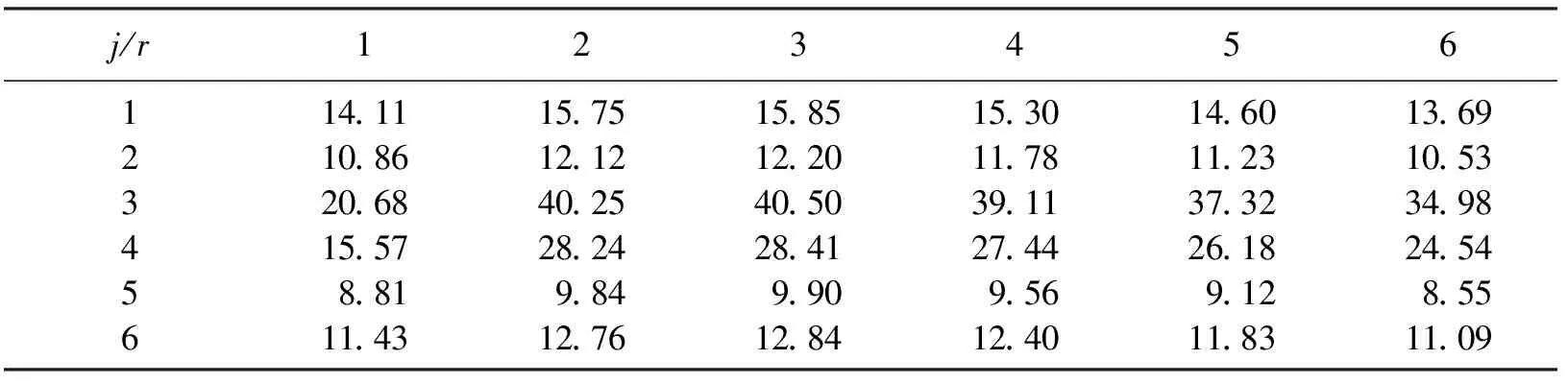
其中:m>0是一个给定的正常数;pj为工件Jj的基础加工时间;aj≤0是工件Jj的学习指数;b(0 问题1 目标是在资源消耗总费用不大于常数U的前提下,求出最优资源分配方案和最优工件排序、最优交货期窗口位置d,ω。极小化目标函数Z1如下: 其中α>0,β>0,γ>0,δ≥0,μ1≥0,μ2≥0为给定常数。 使用文献[14]的三参数表示法,可将上述问题分别表示为 引理1 在最优排序下,机器相邻工件之间无空闲时间。 引理2 对于任一固定排序π=(J[1],J[2],…,J[n]),存在一个最优公共交货期窗口,其中交货期窗口的开始时间d和结束时间ω与某些工件的完工时间一致。 证明 详细证明类似于Mosheiov and Sarig(2009)中引理3,从略。 引理4 问题1中对于给定的工件排序π=⎣J[1],J[2],…,J[n]」,可以得到最优资源分配为 (3) 其中P[j]表示工件的正常加工时间。 证明 其中λ为拉格朗日乘子,分别对λ,u[j]求偏导,令其为0,得 利用式(4)和式(5)得到 由式(6)和式(7)得到式(3)。证毕。 引理5 给定排序π(J[1],J[2],…,J[n]),问题1和2中工件J[k](k=1,2,…,n)的实际加工时间为 (8) 证明 证明过程略。 由此可以得出 其中 将上述算式代入到Z1(π,u*)中,得到 (11) 为了求出最小值,考虑指派问题如下,记 则问题转化为如下指派问题 故针对问题1可以得到下列最优算法 算法1 第1步 依据引理3,求出k与l的数值; 第2步 依据(12)求出νjr的数值,j,r=1,2,…,n; 第3步 计算求解指派问题(13)~(16),分析得到最优排序π*=(J[1],J[2],…,J[n]); 第5步 赋值d=C[k],ω=C[j]。 定理1 对于问题1可以通过求解指派问题在O(n3)时间内求得最优解。 证明 定理结论的正确性由上述分析保证。第1、4、5步可以在O(1)时间内完成,第2、3步需要O(n3)时间内完成,所以算法的时间复杂性为O(n3)。 引理6 问题(2)对于给定排序π=(J[1],J[2],…,J[n])可以得到最优资源分配如下: (17) 证明 对于给定排序π=(J[1],J[2],…,J[n]),拉格朗日函数如下: 其中λ为拉格朗日乘子。分别对λ,u[j]求偏导,分别令其为0,有 由式(18)和式(19)得到 将式(17)代入到Z2中,得到 为了求出最小值,将其转化为指派问题,令 (22) 考虑指派问题如下。令 (23) 则转化为如下指派问题: (24) (25) (26) xjr=0或1j,r=1,2,…,n (27) 算法2 第1步 依据引理3,求得k与l: 第2步 依据式(22)求得τjr,j,r=1,2,…,n; 第3步 求解指派问题式(24)~式(27),得出最优排序π=(J[1],J[2],…,J[n]); 第5步 赋值d=C(k),ω=C(l)。 定理2 问题2可通过利用求解指派问题的方法在O(n3)时间之内计算得到最优解。 证明 证明过程略。 下面给出问题1的一个实例,说明算法的运算过程。 例n=6,α=9,β=12,γ=5,δ=7,μ1=μ2=1,c=0.05,b=0.6,m=4,k=1,q=2,U=80,任务的基础加工时间、学习指数、由于资源分配造成的单位费用由表1给出。 表1 例1的数据Tab.1 Date of example 1 表2 例1中的υjr值Tab.2 υjr of example 1 本文研究带有凸资源分配以及公共交货期窗口的单机排序问题,其中工件加工时间带有截断控制参数学习效应和退化效应.本文列举2种问题:1)限制资源总费用情况下极小化提前惩罚、延误惩罚等总费用;2)带有提前、延误等费用受限的情况下极小化总资源。分别给出目标函数求得最小值的最优算法,并证明问题可在多项式时间内解决,确定最优排序及最优资源分配,给出多项式时间算法。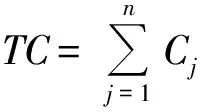
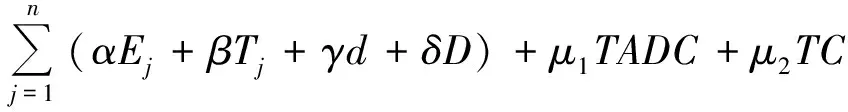
2 最优算法
2.1 最优解性质
2.2 最优算法
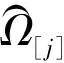
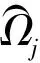
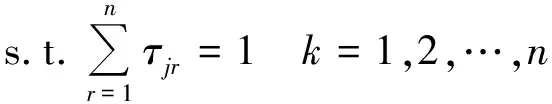
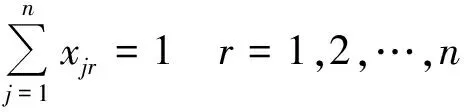

3 结 论