坝岸根石冲刷坍塌数值模拟

，，，

(南昌大学 建筑工程学院，南昌 330031)

1 研究背景

坝垛是为抵御水流直接冲刷堤身而修建的控导工程，是黄河防洪工程体系中的重要组成部分[1]。根石走失的方式主要是冲刷坍塌和冲揭走失2种[2]。冲刷坍塌即坝垛根基周围河床由于长期受到含沙水流的淘刷形成冲刷坑，随着冲刷坑的不断加大，坝岸根石自身稳定遭到破坏，根石发生坍塌[3]。自1954年以来，黄河河务部门对根石走失开展探索试验与研究，分析了走失原因及规律，列举了根石防护整治措施，为实际工程中根石防护积累了经验[4]。田德本[5]从水流条件、根石断面形态等方面对丁坝走失原因进行了分析和探讨，提出坝岸根石受旋涡条件影响最大。崔占峰等[6]引入VOF和空度法，模拟了丁坝附近水流，揭示了丁坝附近水流流动的规律。张红武等[7]通过局部动床模型试验对不同的护根措施进行模拟研究，提出了网罩护根措施。张志军[8]从丁坝冲刷坑的形成及根石走失原因入手，分析了不同工况下各计算公式的适应情况，得出根石走失规律。缑元有[9]通过对河道整治工程中根石受力情况，建立了根石走失的物理模型，得出根石的临界起动尺寸随着含沙量和水流流速的增大而增大。孙桂环等[10]对坝垛冲刷坑的形成机理进行了分析，对黄河下游河道整治工程的冲刷坑进行了公式分析，并对实际河道段冲刷坑的计算参数进行了选取验证。光治河等[11]根据山东黄河河道整治工程现状提出，水流作用、根石粒径和工程布局等都直接影响着坝岸中根石的走失。

由于黄河水流为高含沙水流，并且目前的根石探测技术局限性较大，对根石受冲揭影响的变形量及走失范围多数仍停留在经验性判断[12-14]，根石走失尚无系统的理论分析方法，缺少可用于计算与分析水流特性与根石走失的数值模型。本文基于Flow-3D软件建立根石冲刷坍塌走失特性研究的数值模型，计算水流对黄河坝垛工程的河床冲刷，对冲刷完成后坝垛周围不同区域的泥沙高程面进行分析，对坝垛周围四个位置的边坡进行稳定性分析，得到实际工程中容易发生冲刷坍塌的部位，为河道整治工程设计、防汛抢险预案的制定提供理论依据与技术支撑。

2 数学模型与基本理论

2.1 水流控制方程

连续性方程：

(1)

动量方程：

(2)

(3)

(4)

式中：u，v，w为x，y，z3个方向上的流速分量；Gx，Gy，Gz为x，y，z3个方向上的重力加速度；fx，fy，fz为x，y，z3个方向上的黏滞力加速度；Ax，Ay，Az为x，y，z3个方向上流体面积分数；VF为流体的体积分数；ρ为流体密度；p为作用在流体微元上的压强。

2.2 泥沙控制方程

悬移质方程：

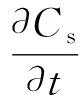
(5)

基于梅耶-彼得的推移质方程：

(6)

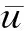
2.3 RNG k-ε模型

RNGk-ε模型控制方程和标准的k-ε模型相似，该模型在模拟计算低强度紊流和具有强剪切力区域时能力较好，因此适用于泥沙冲刷模型。控制方程包括紊动能k方程和紊动能耗散率ε方程。

紊动能k方程为

(7)

紊动能耗散率ε方程为

(8)

2.4 FAVOR技术

Flow-3D采用结构化矩形网格的有限差分法[15-16]，在此基础上应用FAVOR技术，通过计算该区域内物体的面积和体积分数定义复杂几何实体模型。将该技术应用于泥沙模型，并通过FAVOR技术在每个计算时间步里计算出网格内泥沙的面积和体积分数，对冲刷沉积过程中泥沙曲面的变化描述是准确的，解决了在湍流剪切应力作用下，泥沙面变化复杂难以准确模拟的难题。

3 泥沙模型的数学验证

3.1 槽内溃坝水流冲沙试验

泥沙模型采用Fraccarollo等[17]进行的槽内溃坝水流冲沙的物理模型试验进行验证，模型布置见图1(a)。试验在水槽内进行，水槽长为2.5 m，宽为0.1 m，试验开始前在水槽内平铺满0.06 m厚的细沙，泥沙面上以上设置高0.1 m、长1.0 m的水体并拿闸门拦挡，试验模拟闸门快速提起后形成的溃坝水流对泥沙面的冲刷情况。按1∶1比例建立数学模型，如图1(b)。采用0.005 m×0.005 m×0.005 m的网格对计算区域划分见图1(c)，计算总网格数为40万个。

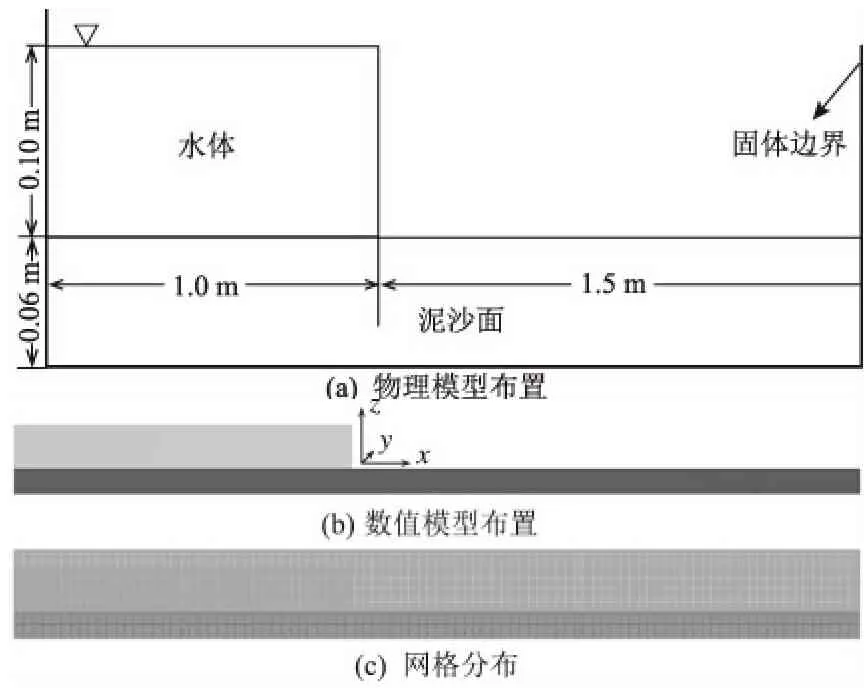
图1模型布置及网格划分
Fig.1Modelandgriddivision

边界条件设定：侧面与底面均设为固壁边界，计算区域上方设一个标准大气压。泥沙设定：泥沙参数设定参考原文献中的泥沙属性，取泥沙中值粒径为3.5 mm，密度为1 540 kg/m3，泥沙休止角取30°。重力加速度为9.81 m/s2。

3.2 计算结果分析

闸门的瞬间提起引起水体形成溃坝水流在槽内传播，造成闸门下游泥沙颗粒的起动，在闸门下游处形成冲刷坑。本文由此分析深泓线处的水面线和泥沙面变化。由图2中物理模型试验与数值模拟计算结果中水面线变化中可知，物理模型试验实测的水面线水舌处水位起伏较大，而数值模拟计算的水面线较为平滑，但两者在数值上基本接近。结合0.25，0.50，0.75，1.00 s时的水面线可以看出物理模型试验结果中水面线均略高于数值模拟的计算值，考虑到物理试验中影响因素较多，卷气现象和泥沙对水流影响较大，认为存在该误差合理。结合图2中泥沙线可以看出，数值模拟结果中泥沙面计算值和物理模型试验实测值接近，说明软件中的泥沙模型计算水流作用下泥沙床面变化准确度高。

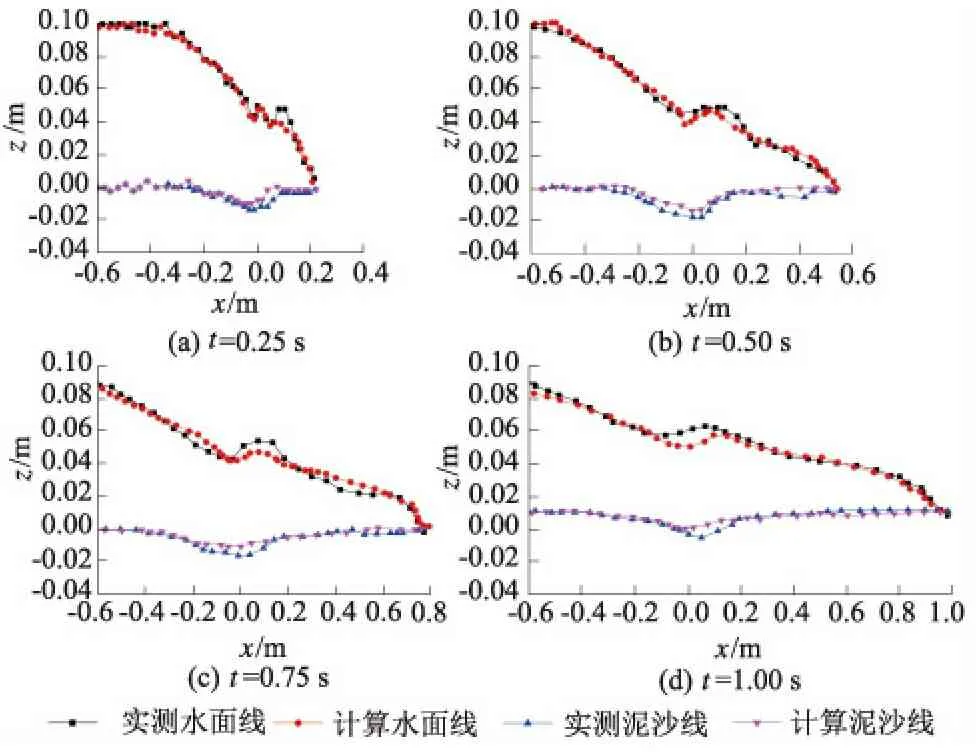
图2不同时刻的泥沙线及水面线
Fig.2Profilesofsedimentandwaterlevelatdifferentinstances

4 根石冲刷坍塌数值模拟研究分析

4.1 根石冲刷坍塌模型建立

利用泥沙模型计算过坝洪水对河床的冲刷，对冲刷完成后坝垛周围不同区域的泥沙高程面进行分析。建立坝垛模型如图3(a)和图3(b)，将所建的实体模型按照1∶1比例导入软件中，计算区域长190 m、宽35 m、高2 m，根石护坡埋入泥沙内部1 m，护坡的坡度为1∶1，在出口处设尾墩控制流量。采用结构化矩形网格划分如图3(c)，网格总数约为110万个。试验模拟洪水对坝垛周围泥沙床面的淘刷，A-A，B-B，C-C，D-D断面分别为离入水口处60，70，80，95 m的监测断面，如图3(d)。

边界条件设定：入口边界采用水位上升边界，设定入口边界为在300 s以内水深由0.5 m上升到1.84 m随后保持在1.84 m；出口边界设定为自由出流边界；壁面及底面均为固壁边界；计算区域上方为一个标准大气压。计算时间为900 s。泥沙设置：泥沙的中值粒径为0.2 mm，密度为2 630 kg/m3，推移质系数取8，携沙系数取0.018，泥沙休止角为32°。

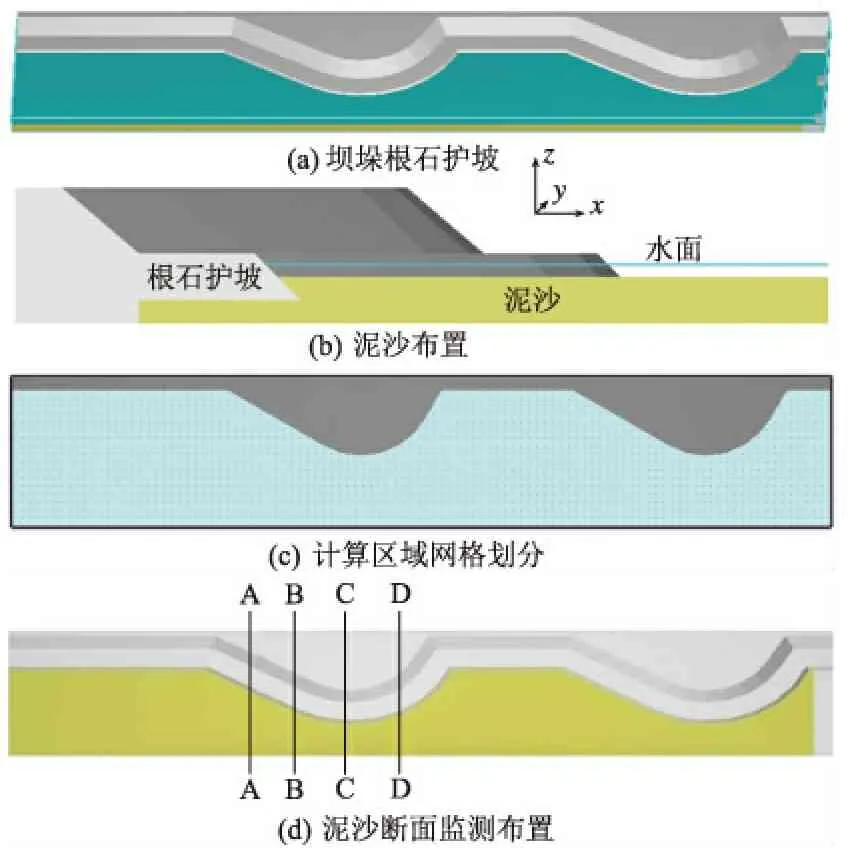
图3坝垛模型计算网格及泥沙断面监测布置
Fig.3Computationmodelofdambuttressandarrangementofsedimentmonitoringsections

4.2 计算结果分析

4.2.1 流速场分析

图4为不同时刻水流过坝垛后的水流矢量图。

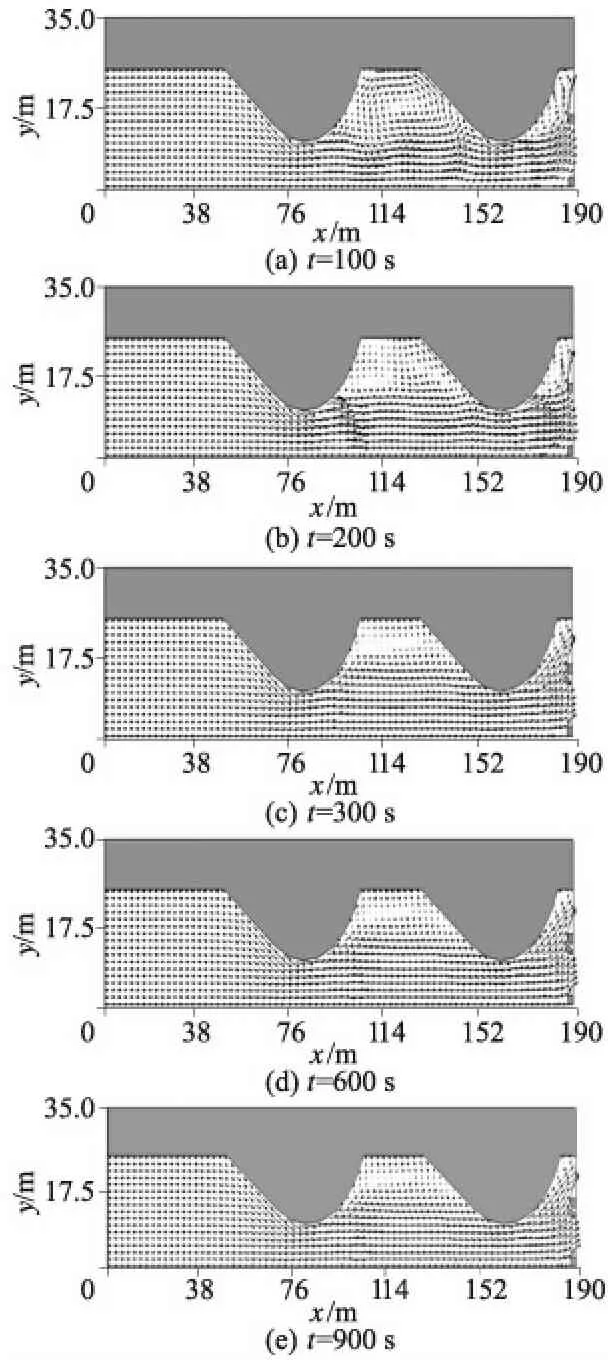
图4不同时刻水流矢量图
Fig.4Flowvectorsatdifferentinstances

水流过坝后由于河床的束窄作用坝前流速变大，并且在坝裆间形成漩涡。由图4中可以看出随着上游来水水位的上涨，坝垛将主流挑向坝对岸，流速较大的区域为坝前和坝对岸处，此处水流的冲刷能力较大，而坝裆间的涡流形态变化复杂，泥沙在此区域可能沉积也可能被带动。

4.2.2 流速分析

图5为不同时刻水流平均流速的等值线图。

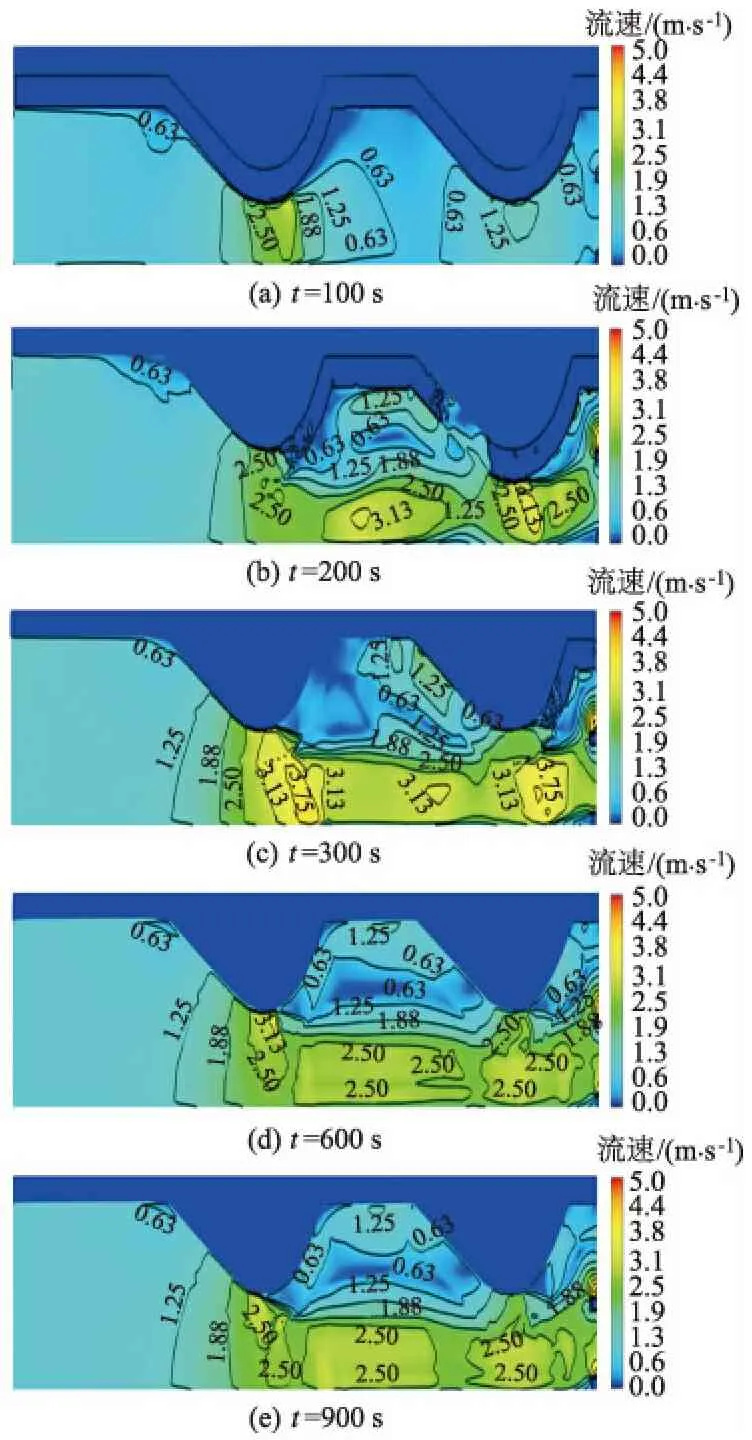
图5不同时刻水流平均流速等值线
Fig.5Contoursofflowvelocityatdifferentinstances

由图5可知：t=100 s时水流过坝，由于坝垛的束窄作用，水流流速在坝前头区域附近最大，迎水面与坝裆间处水流流速小；t=200 s时入口边界水深加高，水流在坝前受挤压作用并被挑向坝垛对岸后一分为二，汇入坝裆间的水流在该处形成漩涡，靠近第2个坝段迎水面根部处水流流速较大和漩涡强度大；t=300 s时入流边界已经达到稳定，水位保持在洪水位1.84 m，水流已漫过整个坝垛段的根石护坡，水流在坝前头处流速达到最大，主流被坝垛挑向对岸，水流在第2个坝垛迎水面根部处流速较大；t=600 s和t=900 s时，由于上游来水已经稳定，因此水流流态变化不大，整体区域的水流流速变化小，坝裆间存在较大的水流漩涡。由系列等值线图可以看出整个过程中迎水面处水流流速小且变化不大，坝前头处水流流速最大，上跨角次之，下跨角处水流流速较小，坝裆间主要是漩涡水流的运动。

4.2.3 泥沙分析

图6是坝垛河床的泥沙输运图，结合图5可知：t=100 s时，水流在坝前头处流速较大，水流带动该处泥沙形成悬移质运输，而其他区域基本无泥沙起动；t=200 s时，坝前头处被带动的泥沙在坝裆间运动，结合图4可知此时坝裆间有水流漩涡的存在；t=300 s时，水流中悬沙浓度较大的区域为坝前头主流区，结合图5可知此时坝前头处水流流速达到最大，过坝水流带动坝前头大部分泥沙形成高含沙水流，被携带的泥沙主要随坝垛对岸主流运动，少部分泥沙进入坝裆间随水流漩涡运动；t=600 s和t=900 s时水流已经稳定，水中的含沙量变化不大，由于冲刷坑的形成加大了坝前头处水深，此时水流的挟沙能力保持稳定减小的趋势。由图6可知：在坝垛冲刷的整个过程中坝前头处水流挟沙能力最大，当水位达到设计洪水位时水流的挟沙能力最强，随着坝前冲坑的形成与上游来水水位的稳定，水流的挟沙能力逐渐减小并继续淘刷周围河床，坝前头处泥沙大部分被主流带往下游，少部分泥沙进入坝裆间随漩涡水流运动。

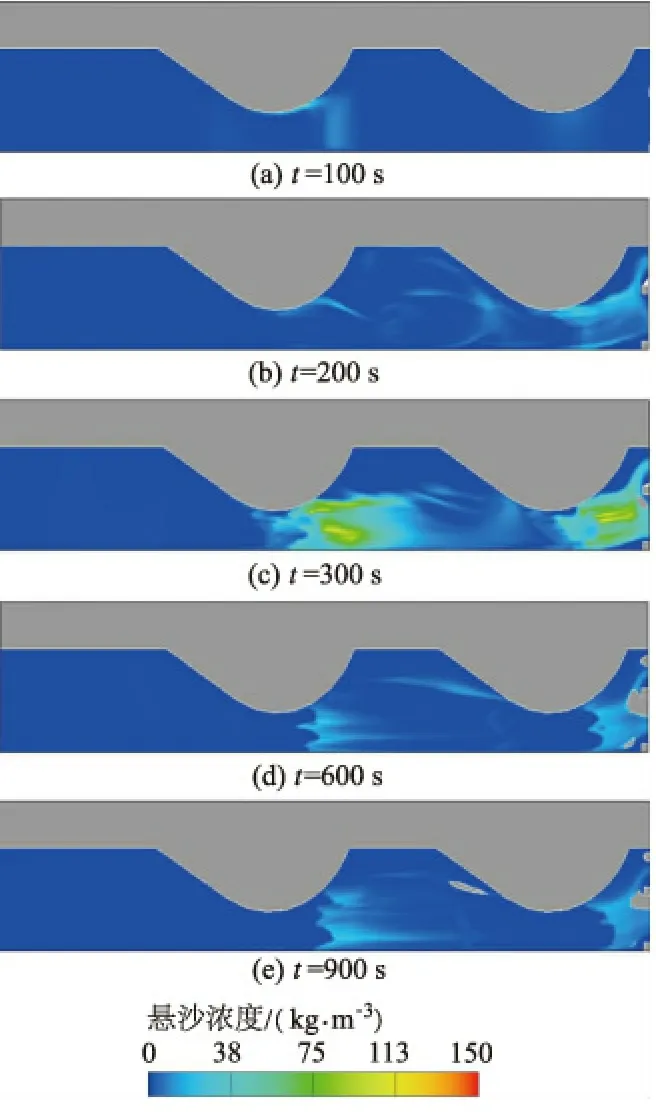
图6坝垛周围河床泥沙输运图
Fig.6Sedimenttransportalongtheriverbed

4.2.4 泥沙床面变化分析

图7是泥沙床面高程等值线，图8是各监测断面的泥沙高程线。

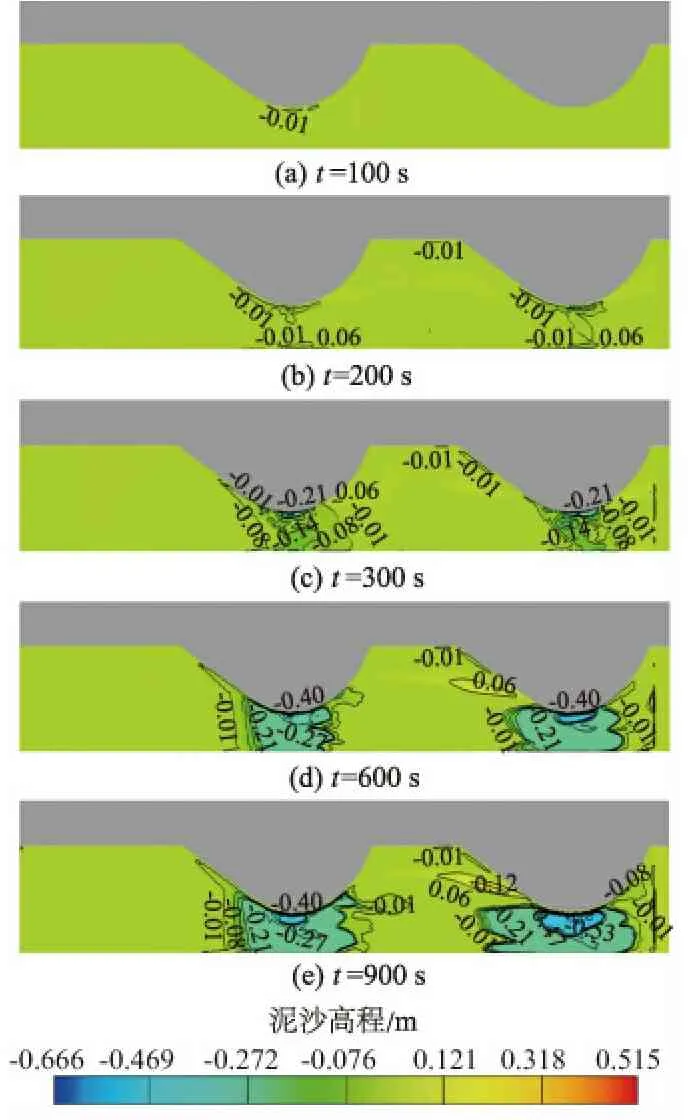
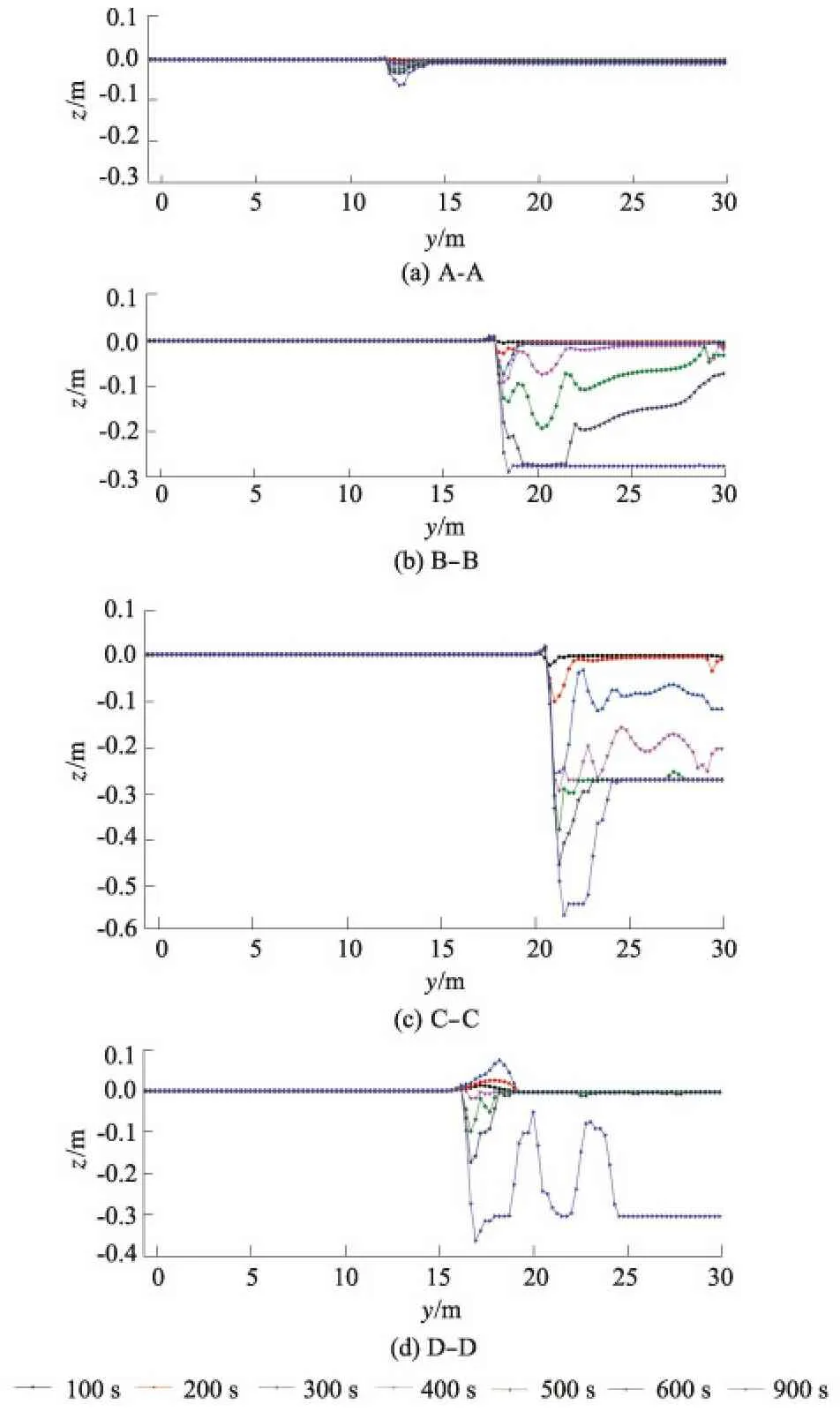
图7 泥沙冲刷高程线变化Fig.7 Variation of sediment line elevation

图8各监测断面泥沙高程线
Fig.8Elevationsofsedimentatmonitoringsections

由图7和图8可知：t=100 s时仅坝前头处有微小冲刷，泥沙床面基本保持平整；t=200 s时坝前头处泥沙冲刷范围变大，结合图4可知坝裆间的漩涡水流对连坝段处造成轻微的淘刷；t=300 s时泥沙床面有轻微变化，坝前头出现冲刷坑，结合图8中C-C监测断面可知坝前冲坑深达到-0.25 m，B-B监测断面显示上跨角处也有冲坑的存在，从图7可知上跨角和坝垛对岸都出现了相应的冲坑，在下跨角前部出现了泥沙淤积现象，D-D断面出现了泥沙的淤积现象，且泥沙淤积高度最大，约为0.07 m；t=600 s时由B-B监测断面可知上跨角处泥沙冲坑深度加深，达-0.25 m，相比于坝前头冲刷坑的纵向发展速度更快，此时水流在上跨角处的泥沙淘刷能力强于坝前头处，D-D断面显示由于水流作用下跨角处的泥沙冲坑逐渐加深，但冲坑的发展速度缓慢；t=900 s时坝前头处的冲坑深度达到约-0.55 m，B-B断面显示水流在600 s以后并没有对冲坑形成纵向的淘刷，而是横向的淘刷，此时冲坑的深度为-0.3m，D-D断面显示600 s以后由于冲刷范围的变大，水流开始淘刷下跨角，下跨角处的冲坑快速发展，深度约为-0.3 m。在整个计算中A-A断面泥沙床面变化程度小，说明该处河床受水流作用影响小。

5 结 论

本文基于Flow-3D软件建立了根石冲刷坍塌走失的数值模型，对实际坝垛工程进行计算得到结论如下：

(1)水流经过坝垛时流速沿坝身逐渐增大，在坝前头处达到最大，上跨角次之，迎水面和下跨角处水流流速较小，坝裆间区域存在较大的水流漩涡。

(2)坝前头处水流挟沙能力最大，该处冲坑出现的时间最早，最终冲坑深最大，该处冲坑前期主要以纵向淘刷为主，随后逐渐向上跨角与下跨角区域横向发展，此两处水流冲刷程度相当，水流淘刷上跨角的时间早于下跨角，此几处被挟带的泥沙在坝裆间由于水流漩涡作用部分沉积形成堆丘。

(3)对各断面的泥沙冲坑进行了对比分析，冲坑深度由大到小依次为坝前头、上跨角、下跨角和迎水面，推断出实际工程中根石护坡在水流冲刷作用下最易出现冲刷坍塌的部位为坝前头处，其次为上跨角与下跨角，上跨角出险时间早于下跨角，迎水面处泥沙冲刷程度很小，该处发生冲刷坍塌险情的几率较小。