液固两相流弯管中砂粒冲蚀实验与数值模拟分析

韩国进，边 江，褚 奇，曹学文

（1. 中海石油（中国）有限公司上海分公司，上海200050；2. 中国石油大学（华东）储运与建筑工程学院）

冲蚀是固体颗粒以一定角度和速度与物体表面接触而造成物体表面质量损失的局部破坏现象[1]，冲蚀发生于石油、航空、机械、冶金等很多设备中[2-3]，冲蚀破坏己经成为材料发生失效、设备出现故障的主要诱导因素之一[4-5]。

国内外学者对冲蚀的数值模拟研究做了大量的工作[6-7]。本文使用实验方法研究了液固两相流弯管的冲蚀形貌，并利用ANSYS/LS-DYNA模型分析了砂粒冲蚀管壁的微观机理。为了便于研究，研究过程中忽略了液体介质水的影响，只研究砂粒对金属靶材的冲蚀行为，因为液固两相流条件下的冲蚀过程中，液体的主要作用是将动能传递给砂粒，使砂粒保持冲击速度，造成金属表面冲蚀质量损失的是砂粒。

1 液固两相流弯管冲蚀实验

1.1 实验装置

液固两相流水平弯管冲蚀实验装置主要由有机玻璃水箱、搅拌器、离心砂浆泵、变频器、电磁流量计、止回阀、隔膜压力表、多普勒测速仪、实验水平弯管和有机玻璃管道等构成。为了测试弯管不同部位处的冲蚀速率，在测试弯管的内壁不同部位设有36个用于安装实验试样的凹槽，实验试样背面有用于连接螺杆的螺孔，试样的尺寸与凹槽的尺寸相吻合，保证实验试样安装后弯管内表面平齐，不影响管道内介质的流态。

1.2 实验材料

选取316L不锈钢作为试样材料，将金属材料块加工成尺寸规格为8 mm×6 mm×5 mm的若干个试样，试样背面有螺孔，实验前先将工作面依次经240#～1 000 #水砂纸打磨，清洗干燥后放入真空干燥器内干燥12 h。

实验的液相介质为去离子水，固体介质为市场上销售的石英砂。将石英砂除杂、酸洗、干燥后，用分子筛筛选出粒径为280～315μm的石英砂。

1.3 冲蚀形貌

液固冲蚀实验后，通过显微镜观察试样的宏观冲蚀形貌。实验前试样表面为水磨砂纸打磨痕迹，打磨划痕沿着流动方向排列。实验后观察发现，41号试样表面粗糙度降低，这主要是由于砂粒的微切削摩擦造成的。44号试样表面出现了不均匀的冲蚀区域，证明垂直于流动方向的径向截面上存在液体介质流动，验证了二次流的存在；45号试样表面形貌变化不明显。

采用3D共聚焦显微镜观察12号与42号试样的冲蚀形貌。位于弯管入口直管段内的12号试样，由于砂粒冲击角度较小，在冲刷剪切作用下，工作面上形成多条沿着表面流体流动方向发展的冲蚀沟槽，主要是由砂粒切削造成的，沟槽坑深为0.20～0.95 μm；42号试样位于轴向角度45°截面位置上，试样表面分布着大小不一的冲蚀坑点，冲蚀坑直径为5～25 μm，深度为 0.25～1.65 μm，坑点开口呈圆形。

2 数值模型的建立与参数确定

由管壁试样宏观和微观冲蚀形貌分析可知，弯管中砂粒对于壁面的冲蚀包括多种冲蚀形式，其中试样表面冲蚀坑主要是由于砂粒直接碰撞导致试样变形造成的，而试样表面的划痕则主要是由于砂粒在试样表面切削造成的。为了深入分析砂粒碰撞试样整个微观过程以及碰撞后试样表面的受力及变形，采用ANSYS/LS-DYNA数值模拟方法模拟砂粒冲蚀金属靶材过程。

2.1 模型的建立

根据液固冲蚀实验情况建立砂粒冲蚀弯管有限元模型，在兼顾数据准确性与计算机性能的前提下，实体单颗粒砂粒冲蚀金属靶材模型采用对称建模，在Y方向的对称面上设定对称约束。直径0.03 cm的球型砂粒模型与0.3 cm×0.1 cm×0.05 cm的靶材模型都为相互独立部分，砂粒与金属靶材之间接触设为面面侵蚀接触，设置砂粒在Y方向为移动约束，在X、Z方向为旋转约束；靶板的非对称面设置为非反射边界条件；采用相应的Johnson-Cook弹塑性材料模型和Gruneisen状态方程建立数值模型。

为确保数值模拟的可靠性，作以下基本假设：磨粒为刚体，碰撞前后无形变；忽略磨粒与靶板初始应力的影响；忽略靶板尺寸对模拟结果的影响；忽略水及外界空气的影响。

2.2 网格划分

计算网格选用拉格朗日网格法，计算网格固定在物体上，网格会随着靶材的变形而变形。采用8节点三维显示实体单元对砂粒与靶材进行空间离散化。网格划分为 92 648个有限元单元，其中靶材为 90 000个实体六面体单元，砂粒为2 648个实体四面体单元。为了提高计算结果的准确性，对中心碰撞区域的网格进行加密，在单元积分时使用单点积分。

2.3 Johnson-Cook(J-C)材料模型

Johnson-Cook材料模型变形过程中的应力公式如下：

式中：A为屈服应力常数；B为应变硬化常数；ε为等效塑性应变；,为应变硬化指数；c为应变率指数；$1为无量纲塑性应变率；*为相应温度，K；-为温度相关系数。

Johnson-Cook材料一个单元的损伤模型公式为：

式中：D为损伤参数，初始时D=0，当D=1时，材料失效；Δ$2为一个时间步的塑性应变增量；$3为当前时间步的应力状态、应变率和温度下的破坏应变。

2.4 Gruneisen状态方程

Gruneisen状态方程可以确定压力与体积的关系，该方程可以判断试样体积是压缩还是扩张。当靶材被撞击时，该状态方程定义压缩状态的公式如下：

式中：p为压力，Pa，E为初始内能，J；7为冲击波速度-质点速度曲线的截距，km/s；S1、S2和SA分别为冲击波速度-质点速度曲线的斜率系数； >为γ0和μ的一阶体积修正量；γ0为Gruneisen常数；56为材料被压缩后的密度，kg/m3。

磨粒选用石英砂，其属性：密度2 650 kg/m3，弹性模量55 GPa，泊松比0.294。316L不锈钢靶板材料属性：密度7 980 kg/m3，弹性模量195 GPa，泊松比0.3，抗拉强度514 MPa。

3 模拟结果与分析

3.1 砂粒冲击速度对冲蚀的影响

在冲击角度为45°的情况下，研究了300 μm砂粒分别在冲击速度为5，10，20，30，40，50 m/s时的冲蚀结果。

数值模拟表明，砂粒速率从5 m/s增加到50 m/s，对应的最大 VonMises应力从 616 MPa增加到 889 MPa；砂粒撞击金属靶材后VonMises应力波从坑点中心以同心圆的方式向四周均匀扩散，VonMises应力波数值由中心向四周递减；速度越大，VonMises应力越大，变形越大，影响范围也越大。

由图1可知，冲蚀坑深度与速度基本成正比例关系，随着砂粒速度的增加，冲蚀坑深度也逐渐增加；速度为5 m/s的时候，冲蚀坑深度为0.14 μm；当速度增加50 m/s后，冲蚀坑深度4.37μm。

3.2 砂粒冲击角度对冲蚀的影响

在冲击速度40 m/s条件下，研究了300 μm砂粒在冲击角度分别为2°，10°，30°，45°，60°和90°情况下的冲蚀结果。

数值模拟表明，冲击角从2°增加到90°，对应靶材VonMises应力不断增加，从228 MPa增加到894 MPa；随着撞击角度的增大，与靶板垂直方向的速度分量增大，VonMises应力数值增大，冲蚀坑深增大；撞击角度较小时，VonMises应力较小，砂粒在金属靶材表面做切削运动，塑性应变区域较长。

由图2可知，冲蚀坑深度随着冲击角度的增加而增加，在60°到90°内上升趋势变缓，在90°时冲蚀坑深达到最大值；冲击速度为40 m/s时的最大冲击坑深为4.64 μm。冲蚀坑的深度由冲击的速度和冲击角度共同决定。

图1 冲击速度与冲蚀深度的关系

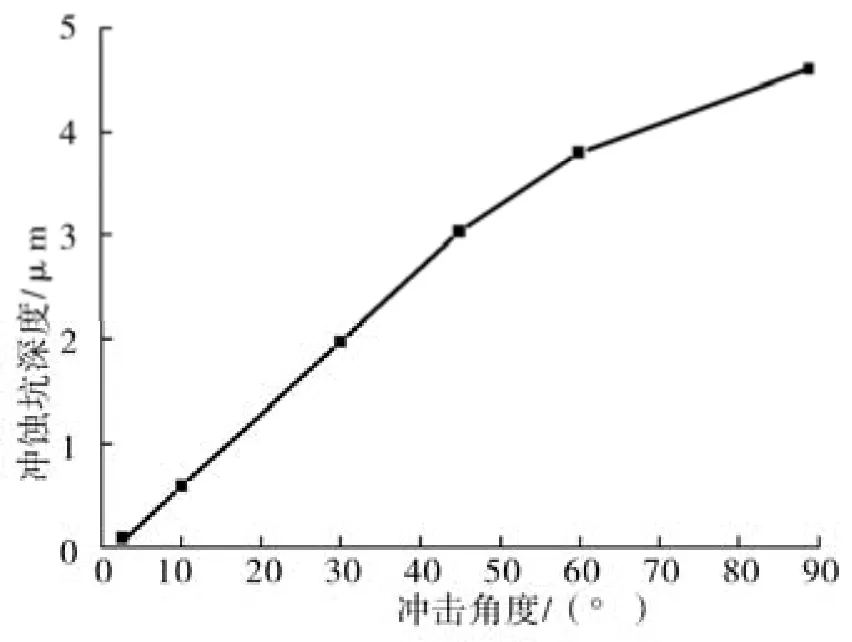
图2 冲击角度与冲蚀深度的关系

4 结论

（1）液固两相流对弯管冲蚀作用显著，冲蚀作用具有明显的方向性。

（2）液固两相流管道中砂粒对管壁的冲蚀形式主要包括冲击变形造成的冲蚀坑、砂粒切削作用造成的划痕以及微切削摩擦。

（3）冲蚀坑深度随着砂粒冲击速度的增大而增大。小角度冲击时砂粒在金属表面做切削运动，随着冲击角度逐渐增大，靶材塑性应变面积减小，冲蚀坑深度增加。