多约束条件下智能RGV 的动态调度策略

张雨萌，胡正凯，王保荣，吴宇航

(1. 华北理工大学 数学建模创新实验室，河北 唐山 063210；2. 华北理工大学 理学院，河北 唐山 063210； 3. 华北理工大学 电气工程学院，河北 唐山 063210；4. 华北理工大学 化学工程学院，河北 唐山 063210； 5. 河北省数据科学与应用重点实验室，河北 唐山 063210；6. 唐山市数据科学重点实验室，河北 唐山 063210)

0 引言

智能加工系统[1]由8 台计算机数控机床（CNC）、1 辆轨道式自动引导车（RGV）、1 条RGV 直线轨道、1 条上料传送带、1 条下料传送带等附属设备组成。RGV 是一个由机械手臂、两只机械手爪和物料清洗槽组成的具有智能控制的小车，其清洗槽每次只能清洗1 个物料，机械手臂前端有2 个手爪，通过旋转可以先后各抓取1 个物料，可以完成上下料作业，通过给CNC 进行取放料，进行动态调度，使其达到最优的生产效率。通过研究确定了RGV 的调度策略、建立RGV 动态调度[2]模型，使得该系统在不同工作情况下具有最优的工作效率。

1 基于路程时间差限定的放料顺序的确定

对零件的加工分析，由于8 个CNC 工作台初始状态是都没有放上需加工的零件的，首先，需要对8 个CNC 工作台进行放料工作，对8 个CNC 工作台进行全排列，选取其中一种排列方式进行第一批放料工作，从而使得每个CNC 工作台都会加工第一批加工器件，由于初始位置是CNC1#和CNC2#正中间，若对8 个CNC 工作台进行全排列，放定第一批的8 个器件，不同放料排列方式之间会产生初始的路程时间差，若选定了最优的排列方式，可以将系统调制最优状态，初试的路程时间差可以忽略不计。可以将放置第一个零件开始时刻定义为系统0 时刻。

对第一批放料的过程进行模拟，将不同顺序放料的零件进行第一批放料，如下式：

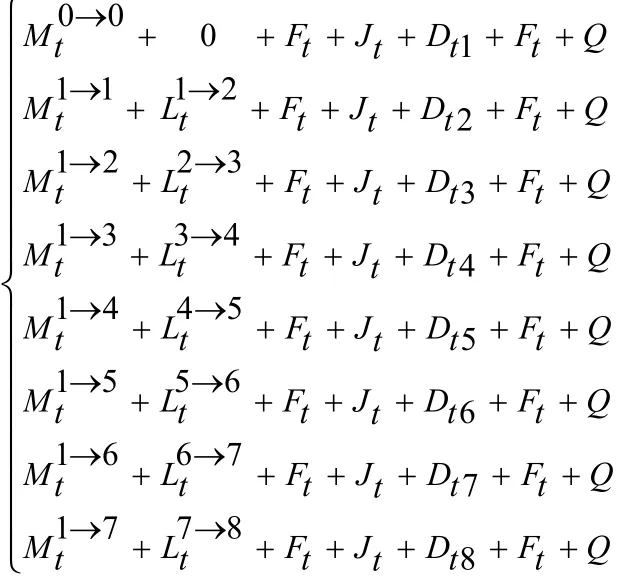
其中，Lit→j表示从i位置到j位置所用时间，Ftm、Ftn表示取放料所用时间，m为1、3、5、7，n为2、4、6、8，Jt表示零件加工时间，Qt表示零件清洗所用时间，En表示第n个零件加工结束时间，Fn表示第n个零件放料结束时间，Dt表示CNC工作台等待RGV小车的时间，Mt1→i表示从0时刻开始计时，从1位置放料开始到第i位置放料完成时间总和。

为了使系统达到最优状态应使得所有的Dt总和达到最小，即此系统达到了最优的工作效率，若初始的Dt总和达到了最小，往后的每批原件都会达到最优，其间还应考虑第一批最后一个零件清洗结束时间和第二批第一个零件的加工结束时间，若第一批最后一个零件清洗结束时间比第二批第一个零件的加工结束时间晚，可以使RGV小车没有停留时间一直处于工作状态。

第一批最后一个零件清洗结束时间为：

第二批第一个零件的加工结束时间为：

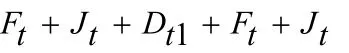
上述两个时间差受 Lt总、Lt8→1、D1t大小所控制的系统，然而 Lt8→1、 D1t大小均受 Lt总所影响，因此通过这个限制条件从8 个CNC 工作台全排列中选取最优的一种排列方式，即可达到系统最优。通过对此限制条件进行求解计算出一道工序下第一组的最优放料顺序为35281746，此种放料顺序生产一批零件耗时最短，从而使整个系统达到最优状态。

2 基于约束条件下的排队论模型

确定好放料顺序后，采用就近原则下的仿真算法，正在服务的CNC 序号用1-8 表示，采用0 表示非加工状态，1 表示加工状态，同时累加CNC 的加工时间，RGV 记为4 个状态，1 表示正在上下料，2 表示正在清洗，3 表示正在移动，0 表示等待状态，CNC 处理工序的组合方式为穷举法。

采用计时循环，以秒为单位，首先分别预计8 台机床的过渡时间，采用DX 表示服务状态，G 表示工序时间，XT 表示CNC 加工累计时间值，Z 表示正在服务的CNC 序号，FZ 表示正要或刚完成某序号的CNC 服务，j 表示8 个工序，X 表示加工或非加工状态，T 表示正在执行周期时间向量。

上式1 表示刚完成服务的CNC，式子2 表示正在服务的CNC,式子3 表示CNC 加工状态，式子4表示CNC 等待状态，通过计算RGV 上下料时间，移动到各CNC 所需的时间，清洗时间等，需要考虑各个CNC 剩余的加工时间与RGV 移动至CNC 的较大时间，因此对RGV 判断判定如下：

上式1 表示处于上下料阶段，式子2 处于清洗阶段，式子3 处于运动阶段，式子4 处于RGV 等待状态。F 表示的是RGV 计数变量，CT 表示执行命令累加时间向量。

综上所述，通过就近原则的仿真得到对于一道工序的器件，在第一组生产数据下可以生产376 件，在第二组生产数据下可以生产359 件，在第三组生产数据下可以生产385 件。

3 两道工序的调度模型的改进

3.1 两道工序的生产过程分析

与上述一道工序的研究相比，两道工序的生产过程实质是在此基础上加入了“分组”的情况，即两个CNN 工作台为一组共同处理物料，不同的分组会使RGV 在移动过程中耗时不同进而产生生产效率的差别[3]。于是，通过改进遗传算法来确定对CNN 的分组情况及RGV 移动的最优路径[4]。

3.2 遗传算法的引入与改进

（1）种群初始化

种群初始化是对遗传个体进行编码，8 个CNN 工作台编号分别为 1、2、3、4、5、6、7、8，RGV有4 个位置编号分别为1、2、3、4，当RGV 处在位置编号1、2、3、4 时分别为CNN 工作台1 和2号、3 和4 号、5 和6 号、7 和8 号提供服务。然后，随机选定4 个工作台作为第一道工序的加工器，另外4 个作为第二道工序的加工器，两种加工器自由结合实现分组，生成种群个体[5]。

（2）选择

计算每个个体的目标函数值。首先，在加工生产物料时，RGV完成最后一个清洗任务所用的时间即为完成此组任务所用的时间，即为一个个体的目标函数值，具体包括上下料时间、加工时间、清洗时间、移动时间。然后，用基于排序的适应度分配方法[7]计算每个个体的适应度fi=2-p+2(p-1)(n-1）/(N-1)p∈[1,2]，其中fi为个体i的适应度，N为种群大小，n为个体在种群中的序位，p为选择压差。最后，计算每个个体的选择概率，通过随机遍历抽样法[7]可得到第i个个体的选择概率Fi。此过程中，选择的个体数目M=N×G，其中M为选择的个数；G为代沟，取值为0.7～0.9。

最后计算每个人个体的选择概率

式中：Fi为第i个个体的选择概率，选取的方式采用随机遍历抽样法。

（3）交叉

交叉操作产生全局较优解。此处采用部分匹配交叉的方法进行交叉操作[8]，首先在2个父个体中随机选择2个交叉点，如表1所示。

表1 有2个插入点的2个父个体Table 1 Two Parents with Two Insertion Points

然后交换中间的基因段，保留2 个父个体中两端与中间段不重复的任务基因段， 并根据中间段的任务对应关系，得到2 个子个体，如表2 所示。

表2 交叉完成后的2 个子个体 Table 2 Two Subindividuals after Cross Completion

（4）变异

通过变异产生更多种类的个体，来局部优化[9]个体。

（5）判断

判断是否满足终止条件，终止条件包括是否到达终止代数，目标值、适应度是否满足要求等[10]。满足终止条件时终止得到CNN 的最优分组，否则开始下一次循环。

通过采用遗传算法迭代与仿真技术的结合[11]，模拟加工过程，主要分为判断清洗料的属性、计算移动后装载的时间变化、记录车的料等。对工序机进行约束，零件1 计数变量用NA 表示，零件2 计数变量用NB 表示，NA＞NB, 在第二道工序的CNC 中取较小者，NA = NB, 在第二道工序的CNC 中取较小者，NB＞NA, 在所有CNC 的较大时间中取较小者。同时记录总加工量、剩余未完成的加工量和组合最佳方案等[12]。 最终得到在第一组生产数据下可以生产211 件，在第二组生产数据下可以生产182件，在第三组生产数据下可以生产222 件。

4 结论

本文给出了基于路程时间差限定的放料顺序的确定模型和基于约束条件下的排队论模型以及对两道加工工序的改进方法，最终确定了最优的放料顺序为35281746，基于排队论模型的加工顺序增加了加工件数。运用遗传算法对两道工序的加工方法进行改进，很大程度上提高了系统的工作效率。