智能RGV 动态调度问题的研究

蒋佳烜，朱天奇，李俊良，吴宇航

(1. 华北理工大学数学建模创新实验室，河北 唐山 063210；2. 华北理工大学理学院，河北 唐山 063210；3. 华北理工大学 机械学院，河北 唐山 063210；4. 华北理工大学机械工程学院，河北 唐山市 063210；5. 华北理工大学，河北 唐山 063210)

0 引言

在传统的自动生产线中，搬运装置一般采用PLC 定时或检测每个工位光电开关的状态等简单的顺序步进控制调度策略。这种“静态”调度的搬运设备需要在线等待在加工工件，并且不能及时适应不确定因素的影响，往往会造成物料传输链的阻塞，形成生产线物流瓶颈，制约生产线设备的利用率和生产率。因此急需设计一种智能加工系统，能够在接到任务后作出最优处理方案，以此来提高生产线的工作效率[1]。

RGV 是一种无人驾驶、能在固定轨道上自由运行的智能车。它根据指令能自动控制移动方向和距离，并自带一个机械手臂、两只机械手爪和物料清洗槽，能够完成上下料及清洗物料等作业任务，但不能智能选择最优化方案，为了更好地解决以上问题，本文提出了以下三种情况，针对这三种情况建立模型来提高生产效率。

（1）一道工序的物料加工作业情况，每台CNC 安装同样的刀具，物料可以在任一台CNC 上加工完成；

（2）两道工序的物料加工作业情况，每个物料的第一和第二道工序分别由两台不同的CNC 依次加工完成；

（3）CNC 在加工过程中可能发生故障（据统计：故障的发生概率约为1%）的情况，每次故障排除（人工处理，未完成的物料报废）时间介于10～20 分钟之间，故障排除后即刻加入作业序列。要求分别考虑一道工序和两道工序的物料加工作业情况。

1 构建一道工序的物料加工作业的RGV 动态调度模型

首先用线性加权的方式将CNC 平均等候时间和RGV 所走路径作为优化目标组合成一个新的评价函数，即多目标距离函数，并由此评价函数来衡量RGV 智能车的操作性能，最终选择在满足约束条件前提下的具有最小距离函数值得RGV 的路径。

1.1 平均等候时间

等候时间，就是指从CNC 完成作业后发出需求信号到RGV 到达此发出需求信号的CNC 所经过的时间。而平均等候时间就是所有CNC 需要等候时间的平均值，这也是RGV 在调度策略中的重要指标[2]。等候时间包括CNC 发出需求信号后，RGV 处理其他CNC 的时间和RGV 从上一个CNC 到发出需求信号的CNC 过程中所需要的时间。可用如下表达式计算：

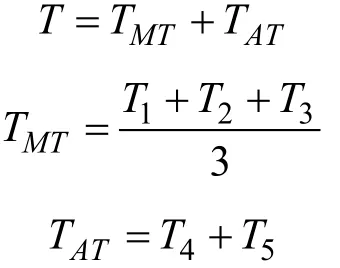
其中T 代表CNC 等待RGV 服务时间，TMT表示RGV 运行到发出需求信号的CNC 所需要的时间。TAT表示RGV 处理其他CNC 的时间。 T1表示RGV 移动一个单位所需要的时间， T2表示RGV 移动两个单位所需要的时间， T3表示移动三个单位所需要的时间。 T4表示上下料所需时间， T5表示清洗所需要的时间。

1.2 用动态规划算法求解RGV 所走路径

设RGV 对CNC 进行一班次连续作业为T 个小时。现有n（n=8）个CNC 可供RGV 进行连续作业处理，这n 种物品的编号分别为1,2, … ,n。每个CNC 需要被处理的时间为t1,t2···,tn，每次RGV 对CNC处理所移动的单位长度为 s1, s2, ···,sn。每个CNC 被处理的次数为 xj（xj≥ 0且为整数， j∈ {1,2,…, n}）。求解如何选择对CNC 进行处理，使RGV 移动的总距离S 达到最大。（其中T , t1, t2,… , tn和 s1, s2,…, sn均为整数）。

建立其模型为：

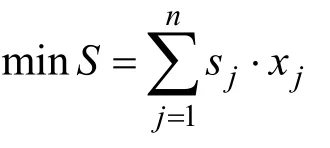
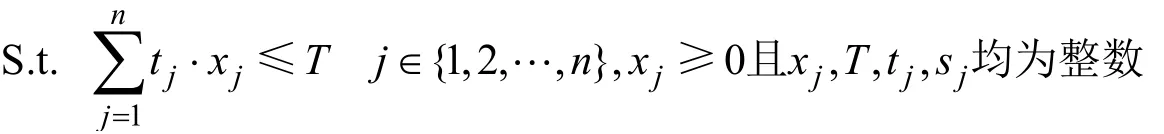
（1）划分阶段K：将8 个CNC 按1,2, … ,n排序，每个阶段RGV 对一台CNC 进行加工处理。

（2）确定决策变量： xk，对第k 个阶段CNC 进行处理的总次数； Tk，对第k 个阶段对CNC 进行作业操作耗费的总时间。

（3）建立状态转移方程：Tk=Tk-1+ tk· xk

（4）建立递归方程：

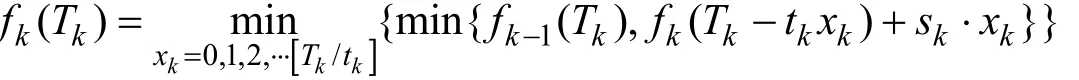
最后根据确定的优化目标，确定多目标距离函数公式为：

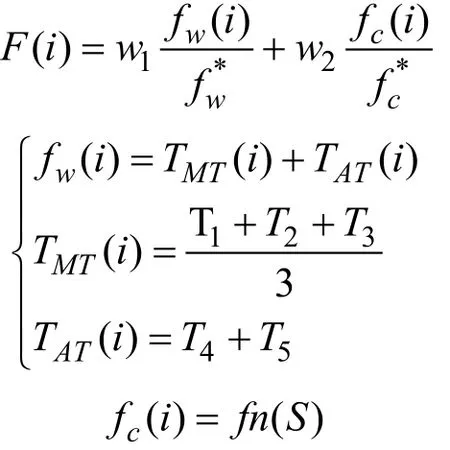
其中， wi即评价函数的参数，0≤ wi≤ 1且 w1+w2= 1； fw( i )为RGV 到达第i 个CNC 时CNC 需要等候的时间， fc( i )表示RGV 到达第i 个CNC 时所需要经过的路程。 fw*表示期望等候时间； fc*表示期望移动距离。

由于这两个指标的量纲不同，为了量纲统一化，需要对对应的目标函数进行统一量纲处理，即在目标函数中引入期望等候时间、期望移动距离 fc*[3]。

1.3 基于排队论的仿真模拟

M/M/1/N/∝排队模型表示CNC 向RGV 发出的需求指令为无限，各个CNC 发送指令相互独立，指令发送规律服从泊松分布，CNC 发送指令平均速率为λ；单服务台，队长限制为N（即系统中最多允许有N 个CNC 在排队），先到先服务，RGV 在为各CNC 服务的时间相互独立，且服从负指数分布，RGV 上下料的平均速率为μ。

图1 智能RGV 的工作流程 Fig.1 Intelligent RGV workflow

根据智能加工系统所给信息对相应的参数进行赋值：

CNC 发送指令的平均速率λ=0.1 个/分钟

RGV 上下料的平均速率μ=1 台/分钟

最多等待服务CNC 台数N=8 台

仿真时间Total_time=480 分钟

根据CNC 发送指令平均速率λ 和RGV 上下料的平均速率为μ 来确定每个CNC 从发送指令到接受上下料服务的时间间隔和上下料时间间隔。上下料间隔时间可以用负指数分布函数exprnd 来生成[4]。由于泊松过程的时间间隔也服从负指数分布，故亦可由此函数生成实现CNC 指令到达的时间间隔。根据该算法对RGV 动态调度进行仿真，得到以下两个仿真曲线。

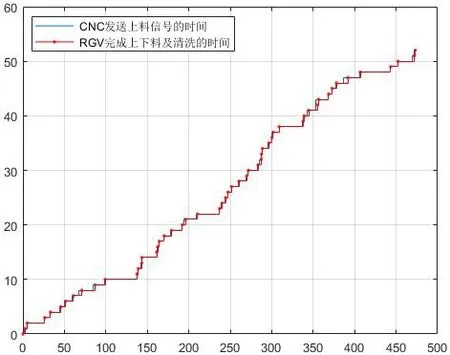
图2 CNC 发送指令时间与RGV 提供服务时间的曲线图 Fig.2 Curve diagram of CNC sending instruction time and RGV providing service time

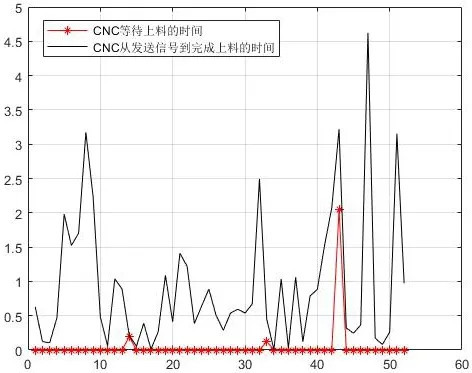
图3 CNC 等待上料时间与发出指令到接受服务时间的曲线图 Fig.3 Curve diagram of CNC waiting for feeding time and sending instructions to receiving service time

通过仿真曲线可以看出建立的RGV 动态调度模型可以很好地指导RGV 完成上下料和清洗工作，在该模型的调度中，CNC 发送指令时间与RGV 提供服务时间高度吻合，说明CNC 从发出需求指令到接受RGV 服务不需要经历很长的等待时间，在该调度模型中RGV 可以在接收指令后及时的提供服务，实现了对时间的准确把握，提高了工作效率。

2 构建两道工序的物料加工作业的RGV 动态调度模型

2.1 CNC 最短流程时间组合

把Johnson算法用于一般的n/m/P/maxF（最长流程时间），目标函数是使最长流程时间最短[5]。maxF等于一批物料最长完工时间Cmax。设n个物料的加工顺序为S={s1,s2,…,sn}，其中si为排在第i位加工的物料的代号。以csik表示物料si在机器Mk上的完工时间，tsik表示物料si在Mk上的加工时间，i=1,2,…,n；k=1,2,…,m，则csik按以下公式计算：

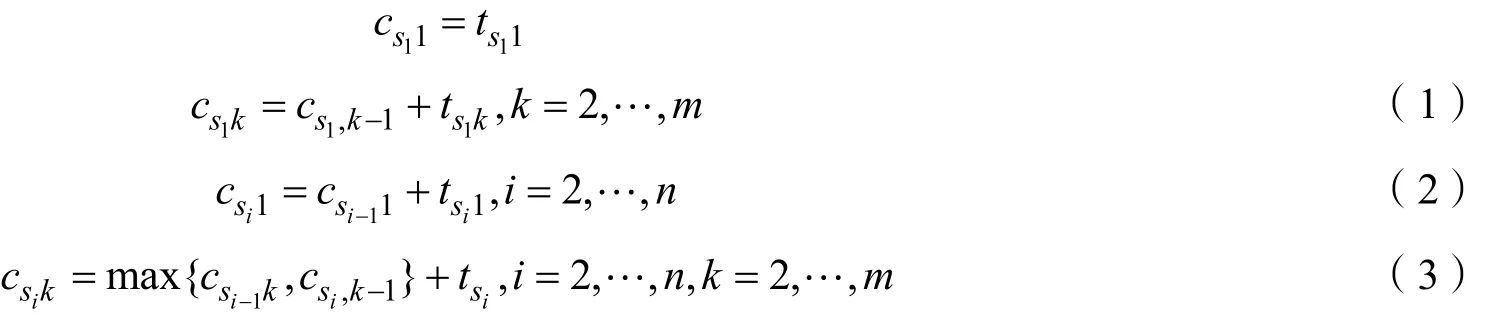
当ri=0, i=1,2, ···, n 时，最大流程时间为

当由（3）式得出csnm时， Fmax就求得了。

对于两道工序的物料加工所需时间为T ，公式为T = t1+ t2，其中 ti为第i 道工序所需加工时间（ i=1,2）。对于两道工序的问题，其中m=4，首先，把8 台机器系统的每两台机器组成一组，产生4个两台机器问题的集合，然后利用Johnson 的两台机器算法改良成四台机器的算法得到4 个加工顺序，最后选择其中最好的一个作为近似最优解。再将8 台机器两两进行组合排列共有4!种可能，将这24种可能全部按Johnson 算法进行最大流程时间的求解，我们取这24 组解中，用时最短的一组排列组合。

2.2 RGV 动态调度优化设计

确定每一道工序在某一具体时间开始设备上加工，保证RGV 所移动距离最小并尽可能对更多的物料进行加工，所以，我们建立如下的目标函数：

式中，Ei为任务提前惩罚； Di为任务拖期惩罚。约束条件如下所述：

（1）完工时间约束：

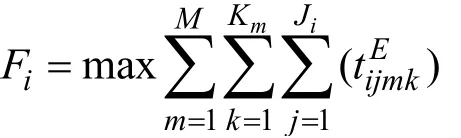
式中， tEijmk为任务i ( i=1,2, ···) 的工序 j ( j=1,2)在设备组 m(m=1,2,3,4)内设备k 的结束加工时间。

（2）动态扰动约束：

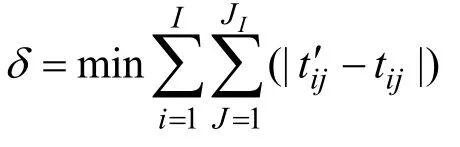
式中 t′ij为调度方案中任务i 的第j 道工序的开工时间； tij为预调度方案中i的第j道工序的开工时间。

设备平衡约束：

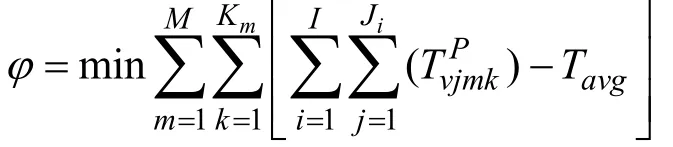
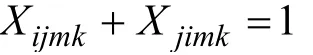
式中， TPvjmk为物料v 的工序j 在设备组m 内设备k 的加工时间； Tavg为所有设备的平均加工时间；Xijmk为0-1 变量，1 表示任务i 在设备组m 中设备k 上先于任务j 加工。

（3）加工时间约束：

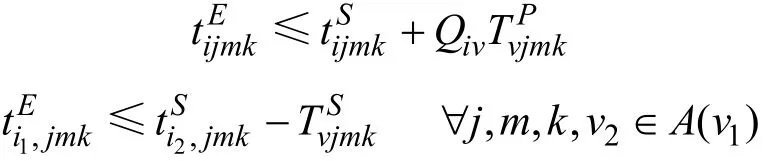
式中，Sijmkt 为任务i 的工序j 在设备组m 内设备k 的开始加工时间。SvjmkT为表示物料v 的工序j 在设备组m 内设备k 的加工准备时间。

3 CNC 发生故障时，别基于一道与两道工序建立RGV 动态调度模型

3.1 序故障情况建立RGV 动态调度模型

1.建立最小加工时间公式

m：CNC总数；

n：待加工物料总数；

si：排在第i个位置的物料，i=1,2,···,n；

S：物料排列集合，S=｛s1,s2,···,sn｝；

p(i,j)：物料i在第j台CNC上的加工时间，相互独立的随机变量，i=1,2,···,n；j=1,2,···,8；

Bj：CNCj的连续可用时间，即CNCj从开始(或修复后重新)运转到下次发生故障期间的运转时间，随机变量j=1,2,···,8；

Rj：CNCj的故障修复时间，随机变量j=1,2,···8；

t(i,j)：物料i在CNCj上的开始加工时刻；

c(i,j)：物料i在CNCj上的完工时刻；

C(i)：物料i在最后一台CNC上的加工完成时刻；

Cmax：所有物料加工的最大完成时刻；

EX：随机变量X的期望值，例如，Ep(i,j)表示加工时间的期望值。

当仅考虑加工时间随机时，对应于排列S的各个物料在每台CNC上的完成时间描述如下：

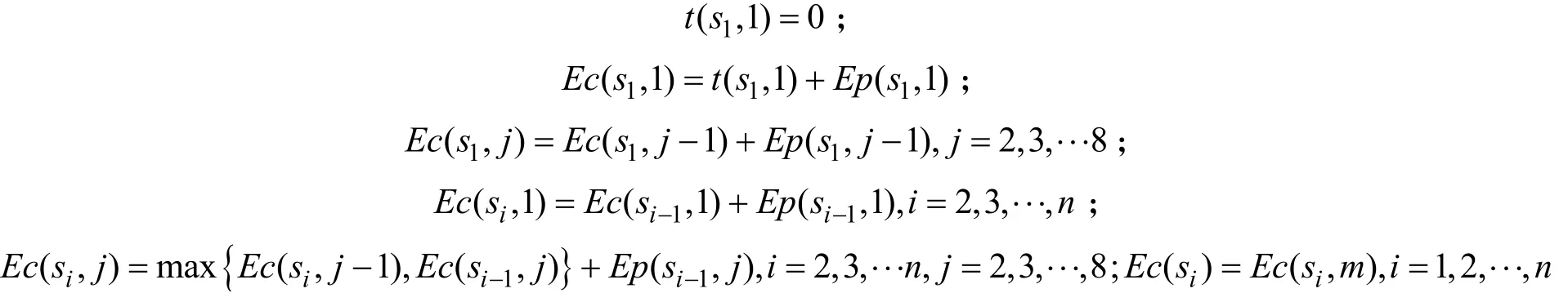
目标是最小化最大完工时间，即

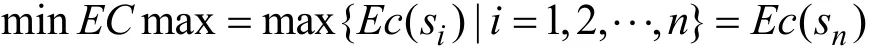
以最小化最大完工时间(ECmax)为目标的 SF-SSP 调度问题就是确定 n 个物料的加工顺序使得ECmax最小，其最优结果记作ECm*a，即：

2.ECmax的求解算法

为合理地计算故障发生的期望时刻和相应的目标值 E Cmax，设计了两类计算规则，用以计算不同CNC 工作方式下的故障发生时刻，并计算物料i (i=1,2, ···,n)在CNC j ( j=1,2, ···, 8)上的完工时间期望值[6]。假设一个物料正在CNC 上加工时CNC 出现故障，修好后，被故障中断的物料的工序在原来已加工的基础上继续加工，其计算规则如下：

假定在初始时刻，所有CNC 可用，且物料可以加工，有：

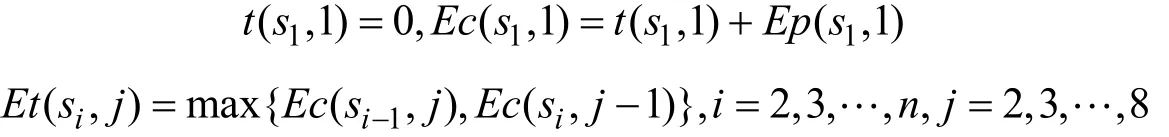
（1）情况1：CNC 从加工第一个物料开始运转，一直运转到故障发生或所有物料结束，任意时刻都可能发生故障。CNCj 的故障时刻期望值为CNCj 的开始工作时刻期望值Et ( s1, j )（或上次故障修复的时刻）与CNC 连续可用时间期望值EBj之和物料在上的完工时间期望值计算如下：

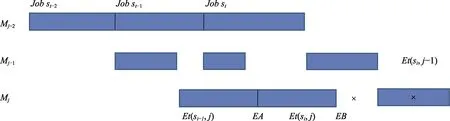
“×”表示故障，“EA”表示故障的期望发生时刻，如图所示，若故障发生在EA 时刻：

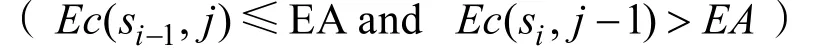
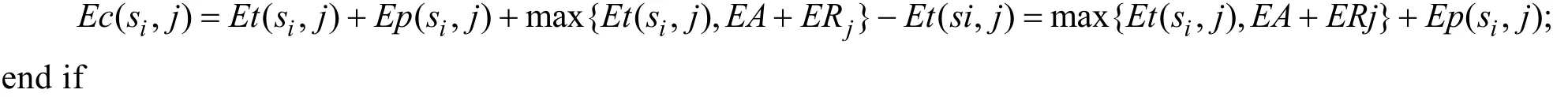
其中，如果

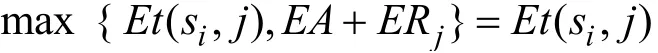
说明故障可以在CNC 正常闲置时间修好，因此这种故障不会影响生产。若故障发生在EB 时刻，则有

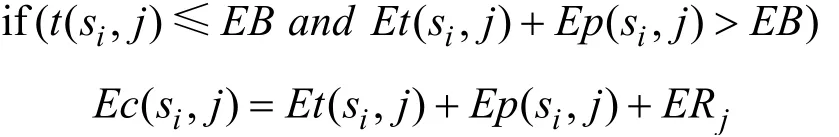
说明这种故障导致物料i 的第j 道工序的完成时间后延jR 。

（2）情况2：CNC 从加工第一个物料开始运转，一直运转到故障发生或所有物料结束，且CNC只有在加工过程中才可能发生故障。当 CNCj 的故障时间期望值存在于非加工时间区间上时，令故障时刻期望值等于，由此保证CNC 在非加工时间内不会出现故障，即不存在图1 中EA 类故障时刻；当不属于区间时，CNC 的故障时刻期望值计算规则同情况 1。物料在上的完工时间期望值计算方法如下：

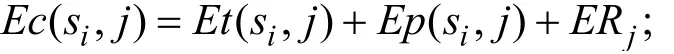
3.2 针对两道工序故障情况建立RGV 动态调度模型

两道工序在一道工序的基础上，增加了CNC 对物料进行不同的加工处理。在问题二已经解出了最优组合。

一道工序与两道工序的共同点：当CNC 发生故障后，不论是当时物料在进行第一道工序还是第二道工序，发生故障后，物料都被报废，都需要从第一道工序进行。因此CNC 出现故障对物料加工的顺序与应用CNC 的顺序发生改变，最终导致物料加工完成的数量减少。

一道工序与两道工序的不同点：两道工序加工时间长，且有最优组合方案，完成一个物料加工相比一道工序的CNC 少。所以，我们只要分别基于问题一二对一道工序与两道工序的物料加工问题，考虑CNC 故障，并依据表一所给的数据，我们就能得出再进行作业操作时，CNC 出现故障，物料进行加工开始的时间与完工的时刻，从而得出我们需要的结果。

4 结论

进行基于排队论的仿真模拟，仿真结果表明在该调度模型中CNC 从发出需求指令到接受RGV 服务不需要经历很长的等待时间，RGV 可以在接收指令后及时的提供服务，实现了对时间的准确把握，提高了工作效率。

CNC 出现故障对物料加工的顺序与应用CNC 的顺序发生改变，最终导致物料加工完成的数量减少。考虑加工时间随机性和对应于排列各个物料在每台CNC 上的完成时间，计算故障发生的期望时刻和相应的目标值，结合前两问的算法建立考虑CNC 可能故障的情况下的RGV 动态调度模型。进而针对RGV 所有情况的调度模型都建立完成。