模糊层次分析下的精准医疗模式评估

魏茜如，伏子尧，胡月佳，吴宇航

（1. 华北理工大学理学院，河北 唐山 063210；2. 华北理工大学电气工程学院，河北 唐山 063210； 3. 华北理工大学数学建模创新实验室，河北 唐山 063210；4. 河北省数据科学与应用重点实验室，河北 唐山 063210； 5. 唐山市数据科学重点实验室，河北 唐山 063210）

0 引言

随着现代医疗水平的发展，病人对医疗机构诊疗效果及诊疗模式的安全性要求越来越高。以糖尿病为例，严格把控病人的血糖水平有助于降低发病率和死亡率。但由于目前多数医院仍保留传统管理体系，患者医疗信息系统不完备，导致病人在血糖方面的检测缺失或波动很大，无法做到临床精准用药与科研结果有效结合[1]。

精准医疗是根据每个患者的个体特征来定制个性化医疗方案的医学新模式，将现代化信息技术和医学方法融为一体，从而科学的认识人体机能与疾病本质，是目前实现临床应用最有效、最安全、最经济的新型医学理念[2]。精准医疗主要体现在诊断、治疗、药物三方面。通过记录病人的临床诊治信息及个体样本信息，采用大数据分析整合信息并对其进行可视化，为每个患者建立一套完善的电子病历，从而形成一套精准的临床诊断报告。同时对疾病的发生及发展情况进行预测，帮助医生实现精准治疗，判断出病因及治疗靶点。针对不同患者明确其最佳使用药物，提高用药效率，减少无效药物或副作用的产生，达到精准用药。

本文提出的模糊层次分析法是一种针对医院治疗模式的综合评价法[3]。该方法将层次分析与模糊评价相结合，利用数学模型较为系统和规范的对多个指标同时进行评价，实现对目标的整体评估及择优。结合医院诊疗数据，将患者各项临床指标分为6 类，并构建3 层指标体系。引入模糊一致判断矩阵，使得模型的一致性检验更加科学便捷。利用模糊层次分析法建立医疗模式评估体系，可以有效评判出医院诊疗效果的决定性指标，改善医院对糖尿病患者的治疗效果，降低患者的再次入院率及治疗成本，从而为精准医疗提供改进方向。

1 精准医疗综合评价指标体系

对精准医疗进行综合评判，需要将医疗水平与患者个体情况相结合。从医院角度来讲，患者的诊疗结果及再次入院率是医疗水平的直接体现；而针对患者个体而言，考虑到经济情况，在保证诊疗效果的前提下应尽可能降低治疗成本，使用药数及诊治步骤少而有效，才算精准医疗。因此要对医疗效果进行评估，需要综合考虑各项指标，建立层次分明的评价体系[4]。

由于精准医疗涉及到指标量大且繁琐，不利于分析，因此将指标进行归类。以美国130 家医院糖尿病患者电子病历做数据背景进行分析，共将指标分为患者背景、入院时生命体征、医院医疗条件、治疗全面性、治疗彻底性及治疗实效性6 类。具体评判指标见图1。

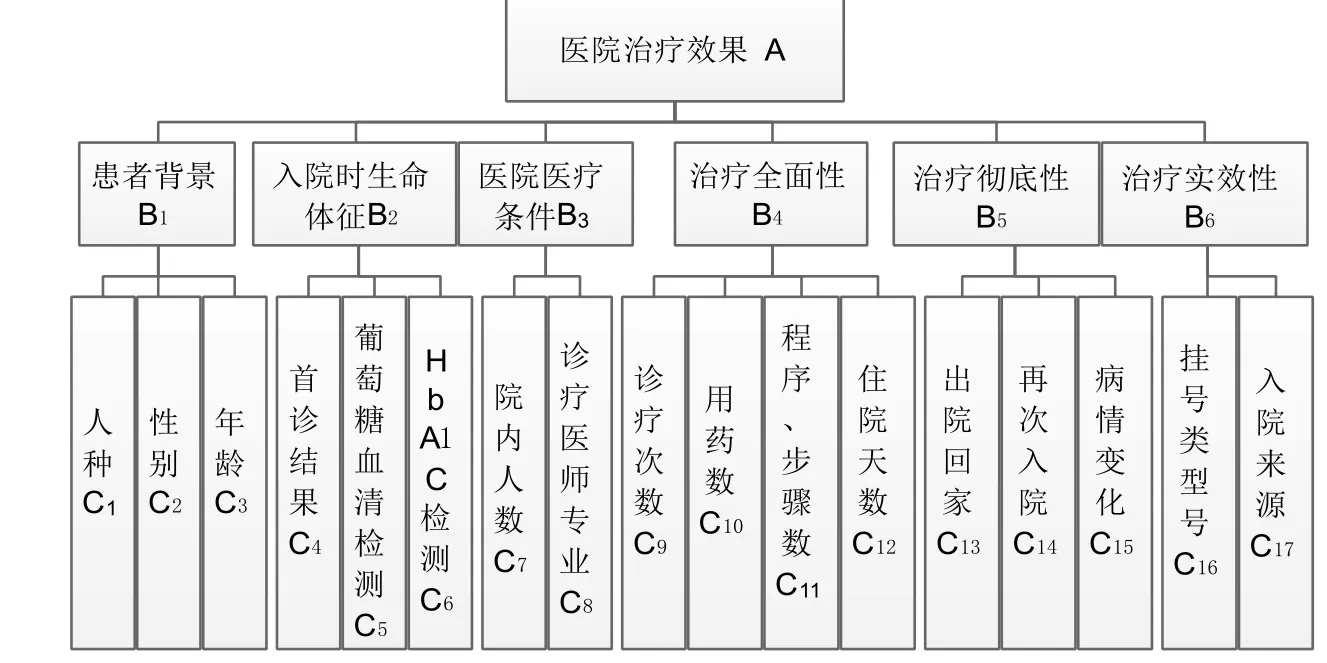
图1 医院治疗效果评判体系 Fig.1 Hospital Therapeutic Effect Evaluation System

以图1 体系中的治疗彻底性评判准则为例，对数据库进行分析[5]。将患者出院后去处进行分类统计，统计结果如图2。

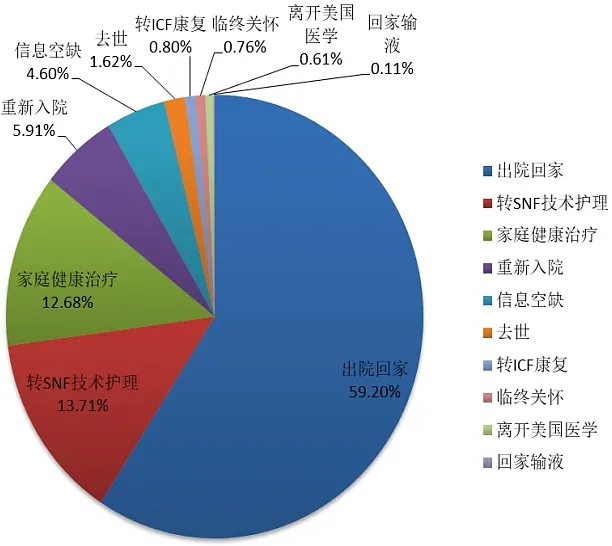
图2 出院去处概率分布图 Fig.2 Probability Distribution Map of Discharge Disposition

从图2 中可知，大部分患者出院后回家休养，没有再次入院或接受其他医疗手段，说明治疗效果较为彻底；还有一部分患者出院后转入SNF 进行技术护理或回家接受家庭治疗，说明医院的治疗没有彻底消除病患；少部分患者出院后又再次入院，说明病情并未得到彻底诊治，需要接受二次治疗；极少数的病人因诊治无效去世或病危接受临终关怀。由此分析出院后不同结果来权衡治疗彻底性对医院治疗效果的影响权重。

2 模糊层次分析法

模糊层次分析法[6]是在构建阶梯层次结构的基础上，结合模糊一致的概念，对多指标构建有序的递阶层次结构的综合评价方法。

2.1 模糊一致矩阵基本概念

若模糊互补矩阵F 不满足模糊一致条件，则对模糊互补矩阵按行求和，根据公式（1）构造出模糊一致矩阵：

2.2 模糊一致矩阵性质

1）rij=0.5，其中i=j；

2）R的第i行和第j列元素之和为m；

3）划掉矩阵R中任意一行及其对应所得子矩阵仍为模糊一致矩阵；

4）R具有中分传递性，即：

a）当λ≥0.5时，若rij≥λ，rjk≥λ，则rik≥λ；

b）当λ≤0.5时，若rij≤λ，rjk≤λ，则rik≤λ。

3 医疗评估的模糊层次分析模型建立

3.1 建立综合评价的递阶层次模型：

构建递阶层次决策模型。模型共分3层，对医院治疗效果的评估为第一层目标层；第二层包含各类评判指标，记为准则层；第三层为具体的各项指标的影响因素，称为因素层，又叫子指标层。

3.2 构造成对比交矩阵

根据表1 中给出的标度法，对第二层中各项指标及第三层的影响因素进行权重评判，两两成对比较，确定其重要程度的隶属度，构造出模糊一致判断矩阵。

表1 0.1-0.9 五标度 Tab.1 Five Scales 0.1-0.9

得到各层次因素间模糊互补矩阵如下：

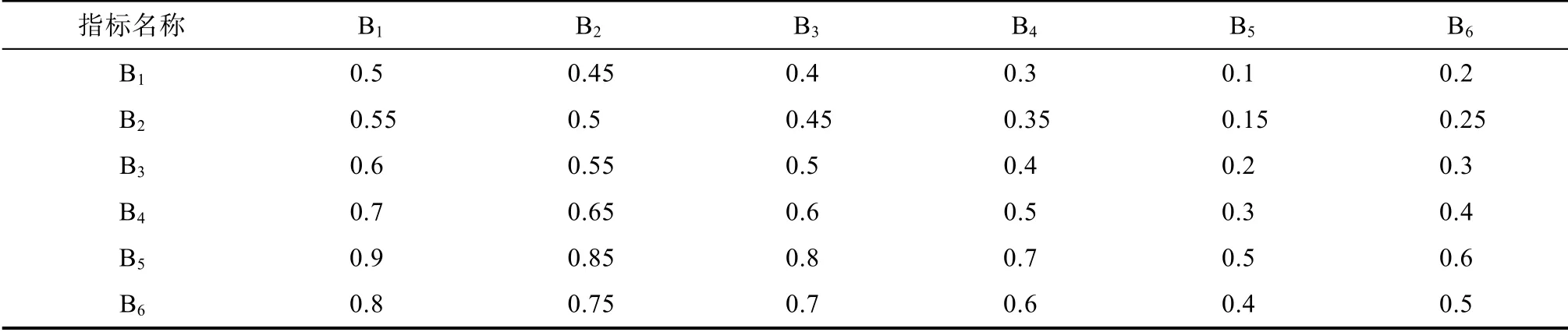
表2 A-B 模糊互补矩阵A Tab.2 A-B Fuzzy Complementary Matrix A

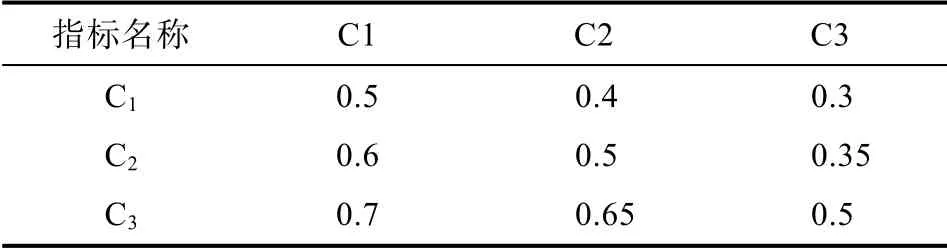
表3 B1-C 模糊互补矩阵B1 Tab.3 B1-C Fuzzy Complementary Matrix B1

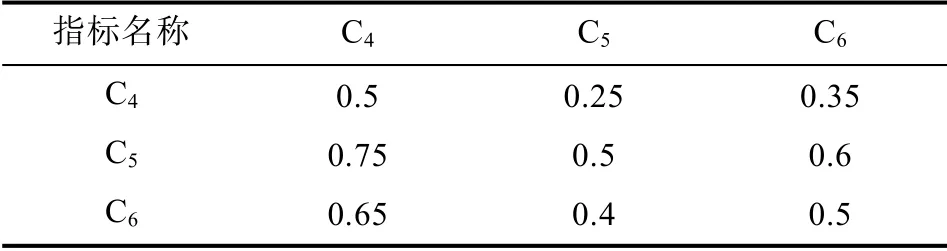
表4 B2-C 模糊互补矩阵B2 Tab.4 B2-C Fuzzy Complementary Matrix B2

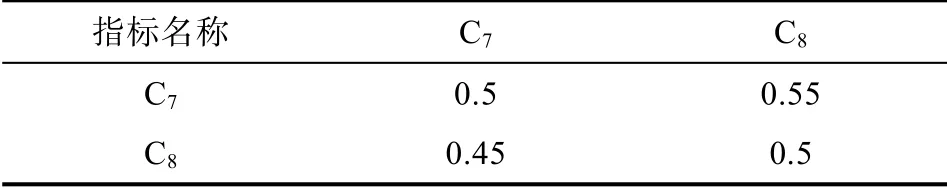
表5 B3-C 模糊互补矩阵B3 Tab.5 B3-C Fuzzy Complementary Matrix B3

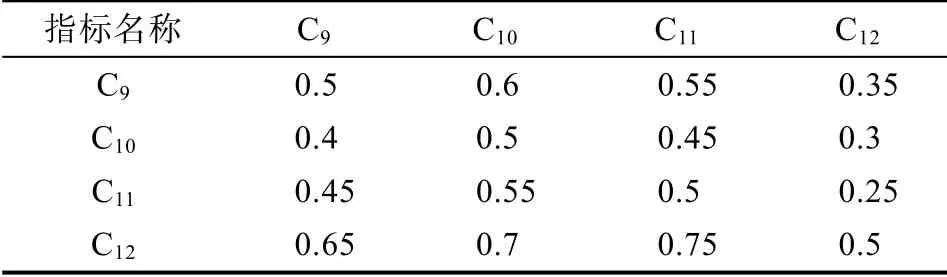
表6 B4-C 模糊互补矩阵B4 Tab.6 B4-C Fuzzy Complementary Matrix B4

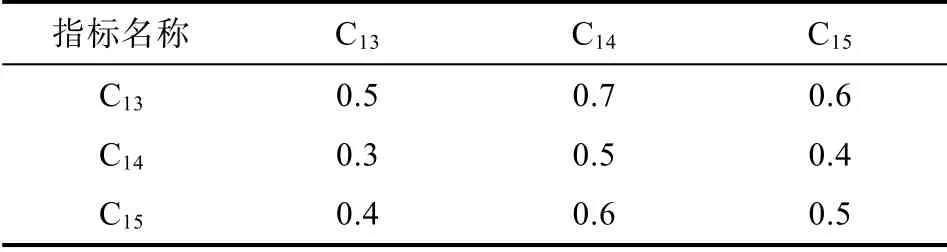
表7 B5-C 模糊互补矩阵B5 Tab.7 B5-C Fuzzy Complementary Matrix B5

表8 B6-C 模糊互补矩阵B6 Tab.8 B6-C Fuzzy Complementary Matrix B6

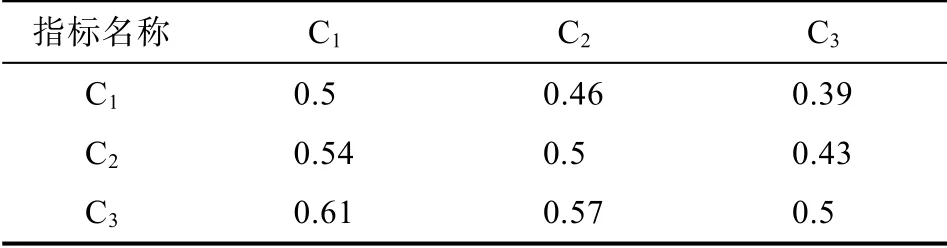
表9 B1-C 模糊一致矩阵B′1 Tab.9 B1-C Fuzzy Consistency Matrix B1

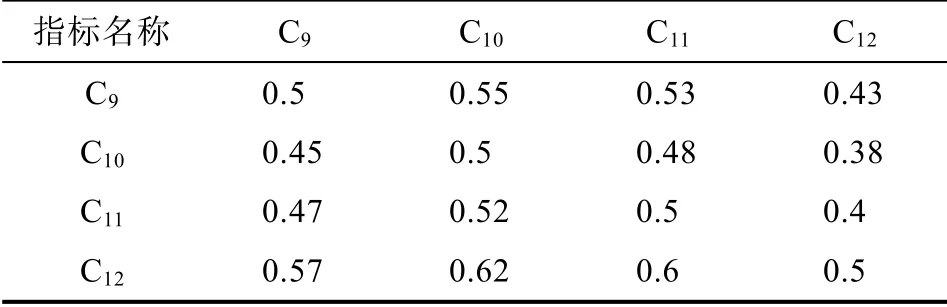
表10 B4-C 模糊一致矩阵B′4 Tab.10 B4-C Fuzzy Consistency Matrix B′4

利用2.1 中给出模糊一致矩阵定义进行判断，得出表3 和表6 中模糊互补矩阵不符合模糊一致矩阵要求，因此利用公式（1）对表3 和表6 进行转换，得到新的矩阵如表9，表10 所示。

3.3 一致性检验

在模糊一致矩阵中，由重要程度隶属度构成的成对比较矩阵的唯一性、互反性及一致性表现为：

由于构建矩阵中的隶属度是有人的主观因素参与的，而人对复杂因子评价采用的两两比较的方法获得的重要性的比值达到一致性的能力较低，因此得到结果会有一定偏差。即最后得到的比较矩阵中仅符合唯一性和互反性，而对一致性很难满足。在不一致可接纳的范围内，利用归一化后得到的矩阵A 的最大特征值的特征向量作为其权向量ω，使得ω满足

根据公式（2）求出A的特征向量与特征根的一致性偏差不大。

若计算得到比较矩阵A的最大特征值为n，即λmax=n，则该矩阵符合一致性原则；若λmax与n偏差较大，则认为该矩阵不符合一致性原则。偏差越大说明此矩阵受人为主观因素影响越大，此时引入一致性指标CI来判断一致性的程度。

当CI=0时，认为矩阵具有完全一致性。CI的数值越大，说明一致性的程度越小，误差越大，直接导致结果不准确。

为确定评价一致性程度的范围，表11给出了Santy关于一致性比率的指标RI及检验系数CR：

当CR0.1≤时认为矩阵具有一致性，即误差在可接受范围内。

表11 平均随机一致性指标RI Tab.11 Average Random Consistency Index RI

3.4 权重计算

B层各指标相对A层权重：ω1=(0.1028,0.1210,0.1393,0.1758,0.2488,0.2123)T，一致性检验结果为CI=-0.6520，CR=-0.5175，即矩阵A的一致性可以接受。

C层因素C1C2C3对指标B′1权重：ω2=(0.2997,0.3266,0.3737)T，一致性检验结果为CI=-0.7563，CR=-1.4543，即矩阵B′1的一致性可以接受。

C层因素C4C5C6对指标B2权重：ω3=（0.2403,0.4147,0.3450）T，一致性检验结果为CI=-0.7831，CR=-1.5060，即矩阵B2的一致性可以接受。

C层因素C7C8对指标B3权重：ω4=（0.5251,0.4749）T，一致性检验结果为CI=-1.0025，即矩阵B3的一致性可以接受。

C层因素C9C10C11C12对指标B′4权重：ω5=（0.2513,0.2261,0.2361,0.2866）T，一致性检验结果为CI=-0.6722，CR=-0.7533，即矩阵B′4的一致性可以接受。

C层因素C13C14C15对指标B5权重：ω6=（0.4019,0.2648,0.3333）T，一致性检验结果为CI=-0.7706，CR=-1.4819，即矩阵B5的一致性可以接受。

C层因素C16C17对指标B6权重：ω7=（0.4495,0.5505）T，一致性检验结果为CI=-1.0101，即矩阵B6的一致性可以接受。

将各级权重分别相乘，得到最终各指标所占治疗效果评判权重百分比如表12。

由表12结果可知，与医院治疗效果评估关系最密切的评判准则是治疗的彻底性。根据各具体指标所占比重不难看出，最有力的评估指标为C17、C13，即患者入院诊治是否及时有效、经过治疗后是否出院回家，直接影响到医院对糖尿病患者的治疗效果。另外，医院的医疗条件、患者入院时所挂诊室是否对症、治疗后的病情变化以及是否再次入院等指标，也可参考评估医院的诊疗效果。

进一步分析这些指标，对美国130家医院的糖尿病患者治疗数据进行处理，利用多元回归分析法统计出：年龄、挂号类型、药物数、检测结果、留院时长变量与再次入院率成负相关；诊疗医师专业、步骤数、糖尿病药物、转院意向变量与再次入院率成正相关。

由此可知，对于提高治病效率与效果问题，需要结合模糊层次分析法建立的指标评判规则，选用转院意向、留院时长、用药量、以及检查病情步骤数。结合再次入院率可知，部分影响因素重合并且作用相反。例如用药量增加可以减少再次入院率，但是增加治疗成本；留院时间增加可以降低再次入院率但是减慢治病效率。但是由于影响因素数量多，而导致单个影响因素变化不会对整体造成巨大影响，可以根据多元回归统计分析出的结果进行调度。

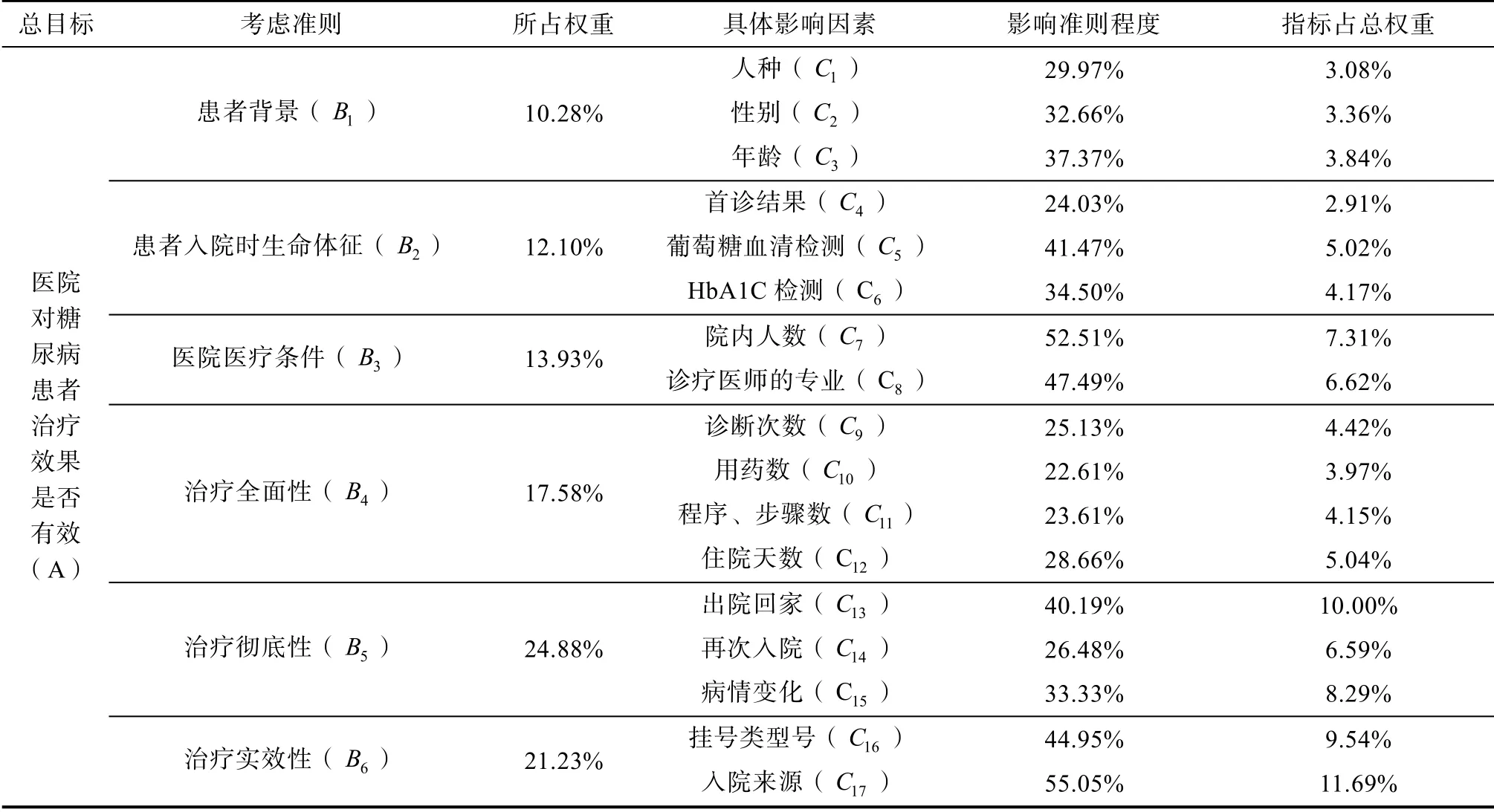
表12 模糊层次分析法指标权重计算结果 Tab.12 Calculation results of index weights of Fuzzy Analytic Hierarchy Process

4 结语

利用模糊层次分析法[8]，有效解决了多指标的综合评价问题。层次分析与模糊评价相结合[9]对指标进行定性与定量综合分析，使得建立起的医疗效果评价系统更准确、更科学。

引入模糊一致判断矩阵，消除了各指标所占权重受人为影响产生的差异，使得指标权重分配更平均，改善了层次分析中一致性检验缺乏科学依据的不足之处，减少了矩阵检验不一致时大量计算、调整的工作量。

模糊层次分析构建的评价体系[10]可有效评估各医疗机构的治疗水平，对于诊疗模式不足之处进行改进，综合考虑了诊疗效果与治疗成本的问题，提出的指标体系与评价结构合理，有一定的推广及实用价值。