基于移动最小二乘的高分辨HDR图像色调映射算法

邹瑞波，廖海泳

（汕头大学工学院，广东 汕头 515063）

0 引言

高动态范围成像（High Dynamic Range Imaging，简称HDRI或HDR），在计算机图形学与电影摄影术中，是用来实现比普通数位图像技术更大曝光动态范围（即更大的明暗差别）的一组技术.高动态范围成像的目的是要正确地记录和重现真实场景中各区域的细节，特别是高亮区和暗区.随着技术的发展，很多成像设备都可以达到很高的分辨率，例如手机拍照的分辨率已经可达2300万像素，在这种情况下，高分辨率HDR图像需要有一个有效和快速的算法.目前有各种各样的HDR色调映射算法，然而很多算法不能同时兼顾保持细节信息和快速这两个特点.例如，基于简单变换函数的算法如文献[1]，虽然速度很快，但是由于压缩亮度的同时也压缩了细节的亮度，使得变换后边缘细节信息不够清晰.另一个方面，基于非线性变换的方法，如WLS算法[2]虽然能够很好地重现细节信息，但是由于计算量极大，甚至不能实现，而不能应用在高分辨率HDR图像.本文提出的色调映射算法首先利用移动最小二乘提取光照分量，也就是在移动窗口中利用最小二乘法提取光照分量.接着根据成像模型对光照分量进行压缩，最后再恢复细节和色彩信息.实验表明本文算法针对高分辨率HDR图像能够很好地保持和重现细节信息，而且速度比WLS算法快.

1 高分辨率HDR图像色调映射

1.1 图像分解与压缩模型

根据成像模型[3]，图像f（p）可以表示为：

其中p表示图像像素的位置，i（p）为光照分量，r（p）称为反射分量.即图像在位置p的像素值由这两者的乘积得到.光照分量i（p）的大小反应了在自然场景中照射到物体的光能的多少.根据我们的日常经验可以知道，自然场景中的光照一般都是局部均匀，虽然有不同明暗的区别，但是从信号处理的角度看，所含的细节信息比较少.所以我们可以通过改变i（p）的值来压缩图像的亮度范围，最终使得亮区和暗区的信息能够同时较好地显示出来.反射分量r（p）的幅值相比之下往往较小，但富含细节，能够真实反映场景中的各种信息.因此这一分量的信息要尽量保存.

基于前面的理论分析，我们利用如下模型进行压缩，重建LDR图像：

其中f′（p）为压缩重建后的LDR图像.c为压缩系数.根据幂函数的性质[4]，我们可以知道当c＞1时，将对暗区像素值进行压缩，同时放大亮区像素值范围；反过来，当c＜1时，将对暗区像素值范围进行放大，同时压缩亮区像素值范围，如图1所示.通过大量的观察我们发现绝大部分的HDR图像像素值主要集中在灰度直方图的左边，而右边的高像素值所占比例极少.图2 Memorial的灰度直方图就是一个经典的例子.综上可知，为了达到增强暗区细节对比度的效果，c的设置一般要在小于1.

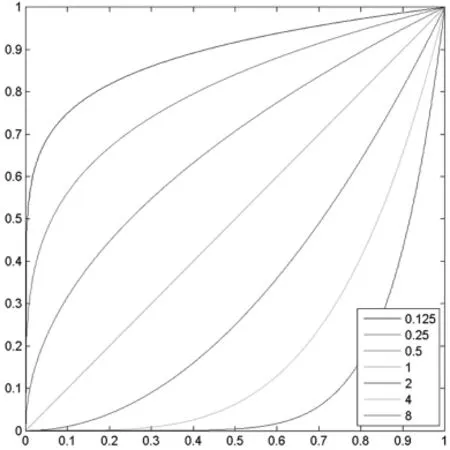
图1 幂函数

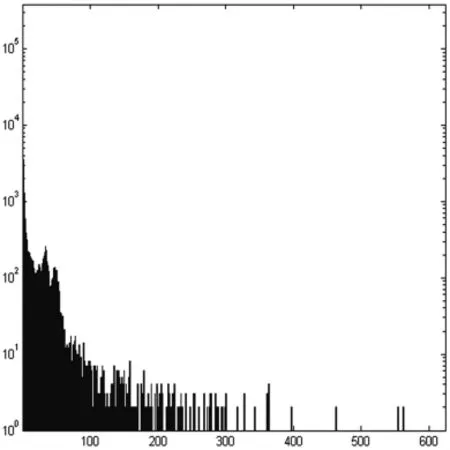
图2 Memorial灰度直方图

1.2 算法框架

我们先给出整个算法的主要步骤，再对关键步骤进行解释.

算法步骤如图3所示

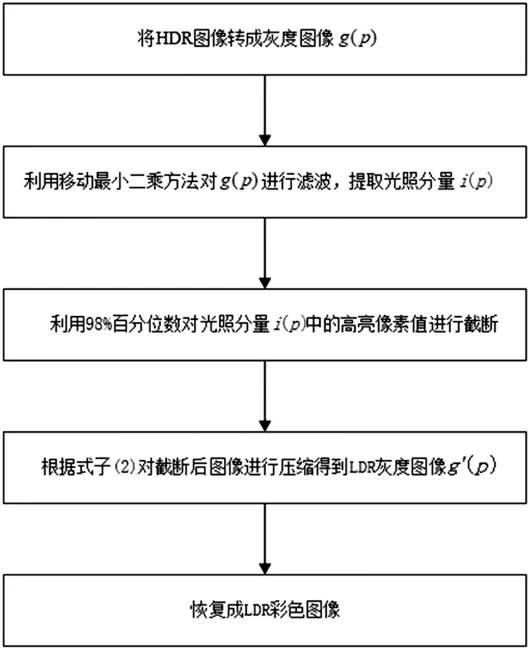
图3 算法框架

在第二部分中我们利用移动最小二乘方法提取光照分量.移动最小二乘方法在下一节中将进行详细介绍.从图2可以观察到HDR图像亮区的像素值比其他区大得多，而且亮区的像素在直方图中所占比例非常小.根据这个特点，我们在第三部分中利用98%百分位数对高亮像素值进行截断，这样可以有效的缩短动态域范围，进而达到压缩的目的.

2 光照分量的提取

由于光照分量具有局部均匀的特点，如果采用传统的平滑滤波器进行滤波会导致边缘模糊，从而使得重建后的图像中边缘有光晕的问题.为了避免这个问题，我们可以采用各种边缘保持滤波器进行提取，例如WLS滤波器[2]，双边滤波器[5]，TV滤波器[6]等.由于WLS滤波器具有很好的边缘保持效果，下面主要介绍WLS滤波器的基本原理.

2.1 最小二乘滤波器

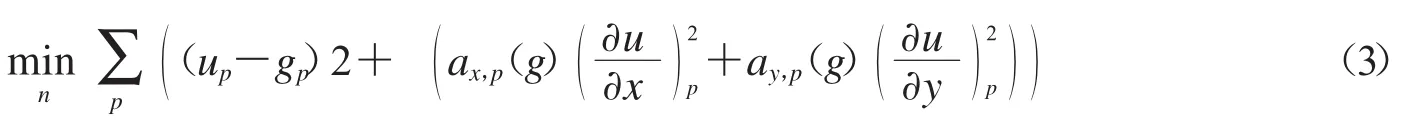
给定灰度图像g（p），WLS滤波器通过求解来得到光照分量u（为了在下文避免符号容易混淆问题，这里使用u表示光照分量，而不是前面的i（p））.在式子（3）中第一项是数据保真项，用来保证u和g尽量接近，第二项是正则化项，用来控制所求u的平滑程度[7].是一个正则化参数， 越大则所求的光照分量u越平滑.而关于平滑权重的计算，我们参考了文献[8]的方法，具体如公式4所示

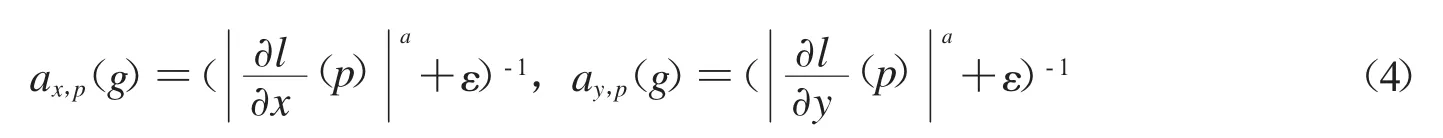
其中I＝log（g）.ax，p（g），ay，p（g）分别表示在像素p位置求偏导数.α取值一般在[1.2，2]的范围.ε是一个很小的值，例如，ε＝10－4，甚至更小，主要用来避免零做除数.式子（3）是一个二次型，对其求导可得到一个线性方程组

其中矩阵

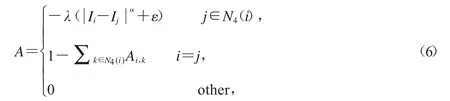
这里下标i，j表示图像中的像素，N4（i）表示像素i的4-邻域.u，g分别是光照分量和原图像按列形成的列向量.系数矩阵A是一个大型的稀疏矩阵，其大小为N×N，对应图像的像素个数为N.图4是N＝100时，系数矩阵A非零元素的分布模式.可以看到A是一个主对角带状的稀疏矩阵.值得一提的是，当图像分辨率为1000×1000时，矩阵A的大小为106×106.而现在日常生活中图像分辨率至少是这个级别，甚至更大，所以WLS滤波器求解一个大型稀疏线性方程组将会更加困难.

求解大型稀疏方程组有迭代法[9]，直接法[10]两大类.后面我们采用的是直接法求解.关于直接法，具体可参考方献[11].

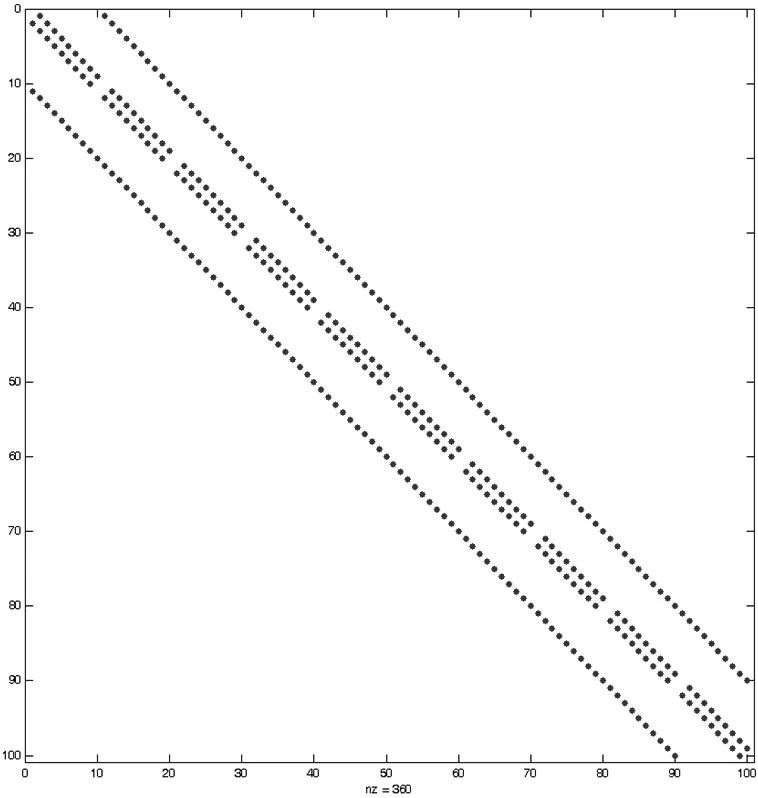
图4 稀疏矩阵

2.2 移动最小二乘滤波器

基于WLS滤波器的色调映射方法具有很好的视觉效果，然而由于需要求解大型方程组，不适合高分辨率图像.高分辨率图像的像素个数一般可以达到107这个级别，如果直接对整个图像进行求解线性方程组，计算量相当惊人，几乎不可能实现.受平滑滤波器[12]和图像分块处理算法[13]启发，对高分辨率图像，我们采用平滑滤波器的框架，在移动窗口里面进行最小二乘滤波.具体如图5所示，设置一个移动窗口，该窗口首先位于图像的左上角，先在窗口里面利用式子（5）求出光照分量，再将窗口以步长h向右移动，接着求出新位置的光照分量，以此类推，一直到图像的右边边界.然后窗口下移步长h，再从左到右移动滤波，重复之前步骤，直到窗口到达图像的右下角.对于窗口移动过程中的重叠区域，我们采用加权平均的方式计算该重叠区域的像素值.

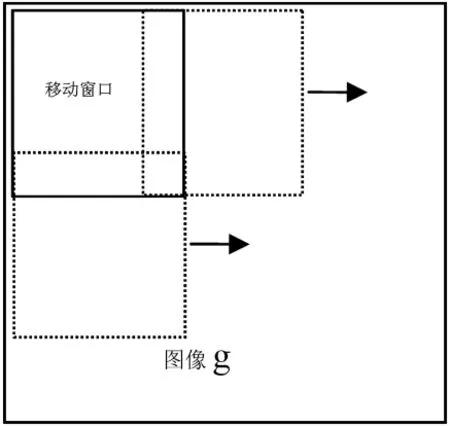
图5 稀疏矩阵

为了验证本文算法是否有效，我们将本文算的滤波效果与WLS滤波的效果进行比较，具体见图6.其中图6（a）测试图片来自文献[2].（b）（d）（f）是 WLS 滤波的效果，（c）（e）（g）是移动最小二乘滤波的效果，可以看出本文算法可以达到WLS滤波器[2]的效果，这说明了本文算法的有效性.

图6 对比WLS和本文算法对于边缘保持的效果

在移动最小二乘滤波器算法里面需要设置两个参数，一个是移动窗口的大小，一个是移动窗口的步长（同时决定了相邻窗口的重叠区域）.下面讨论这两个参数的选择对滤波效果和速度的影响.显然，移动窗口的设置不能太小也不能太大，因为太小的话而导致重叠区域增多，从而影响整体的计算速度，相反，如果太大会增加在移动窗口中求解线性方程组的难度.移动窗口的步长会影响到相邻窗口的重叠区域，例如，步长太大，则相邻窗口的重叠区域太小，则可能会造成块状效应.反之，如果太小，则相邻窗口的重叠区域较大，会增加一些不必要的计算量，从而影响计算速度.经过实验我们发现，只要相邻移动窗口有至少百分之十的重叠区域就可以达到WLS滤波器的效果.为了更好地测试窗口大小对计算速度的影响，我们采用不同大小的窗口对图6（a）进行测试，在保证与WLS滤波器一样效果和使用最长步长的情况下，表1列出了窗口大小和滤波计算时间的结果.可以看出当窗口大小为200×200时或以下时，计算速度较快.使用这样大小窗口的另一个好处是：在这种情况下，求解线性方程组不需要占用大量的内存资源.

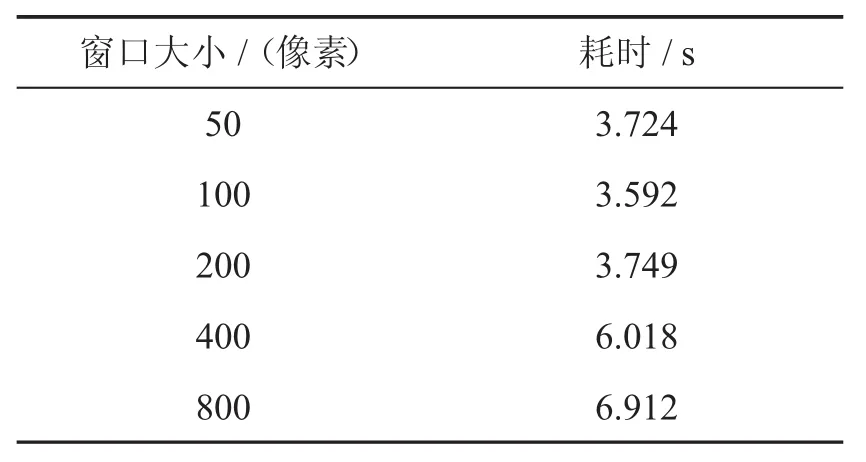
表1 不同窗口大小对计算时间的影响

3 实验结果与分析

在实验中本文采用的硬件设备为：Core i5-7200U，@2.50Hz双核处理器，Nvidia GeForce 920MX（2GB）显卡，8GB内存.软件环境为：Ubuntu16.04＋MATLAB.由于篇幅所限，下面展示两幅具有代表性的HDR图像及其测试效果，其中图6（a）Oxford Church HDR图像的分辨率为1 013×1 200.图7（a）Narrow Path HDR图像的分辨率为8 192×4 096.图7（b）到图7（d）分别是本文算法，WLS 算法[2]，双边滤波算法[5]处理后得到结果.可以看到，本文算法与WLS算法非常接近，而图7（d）整体上细节没有图7（b）和图7（c）清晰，特别是窗口玻璃上的细节，这是由于双边滤波器的边缘保持效果没有WLS滤波器好这一特点决定的，原因具体见文献[2].同样的，通过比较图8（b）和图8（c），我们可以观察本文算法在细节方面明显比双边滤波器清晰，特别是石头后面远处的山这些区域.需要说明的是，由于图8（a）Narrow Path HDR图像的分辨率过高，WLS滤波器需要求解一个超大规模的线性方程组而导致内存溢出，无法得到最终的结果.

最后，我们采用不同的HDR图像进行测试，比较3个算法的处理时间，结果如表2所示.当图像分辨率比较大时，本文算法的计算时间明显比WLS算法少，而且能够处理任意分辨率的HDR图像，后者是WLS算法所做不到的.虽然双边滤波明显比其他两种算法快，但是从前面的实验结果图7，图8可知基于双边滤波的算法整体上细节没有比其他两种算法清晰.

图7 Oxford Church HDR图像的算法效果比较

图8 Narrow Path HDR图像的算法效果比较

4 总结

近年来，随着成像设备分辨率的不断提高，高分辨率HDR图像受到越来越多人的青睐.WLS算法是一个很优秀的色调映射算法，然而对于高分辨率的HDR图像，WLS算法由于需要求解超大规模的线性方程组而导致无法得到最终结果.本文提出的移动最小二乘滤波算法可以克服这一缺点，同时可以很好地保持图像边缘信息.实验结果表明，本文中所提的色调映射算法能很好地保持图像细节，能够处理任意分辨率的HDR图像.

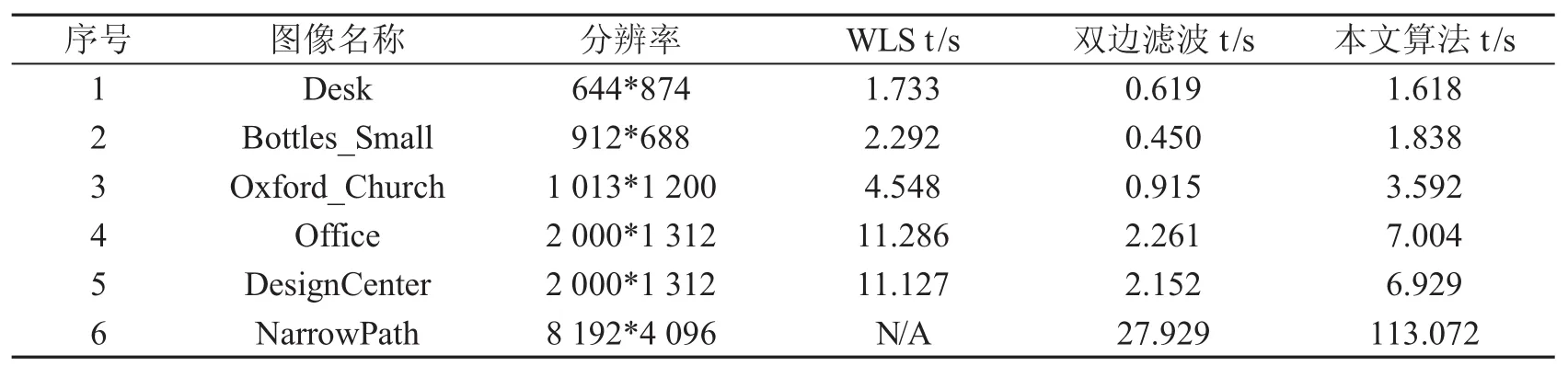
表2 本文算法和WLS算法处理时间比较