Malaga大气湍流信道下副载波调制系统相位噪声分析

柯熙政，王晨昊，陈丹



Malaga大气湍流信道下副载波调制系统相位噪声分析

柯熙政，王晨昊，陈丹

（西安理工大学自动化与信息工程学院，陕西 西安 710048）

Malaga大气湍流信道下研究了系统解调模块的相位噪声对无线光副载波相移键控调制系统性能的影响。结合傅里叶级数及MeijerG函数性质，得到了Malaga大气湍流信道模型瞬时信噪比的概率密度函数，在Malaga大气湍流信道下推导了接收信号相位的傅里叶级数以及相位噪声影响无线光副载波MPSK调制误符号率的渐进表达式，在不同调制阶数和光强起伏方差下分析了相位噪声对系统误符号率的影响。数值结果表明，当相位噪声较小时，系统误符号率随着光强起伏方差增大而增大，相位噪声较大时，误符号率平层的出现受调制阶数的影响大于受湍流强度的影响，且随着调制阶数的升高，误符号率平层出现时所对应的平均电信噪比越低。

无线光通信；Malaga大气湍流信道；副载波调制；相位噪声；平均误符号率

1 引言

无线光通信具有速率高、带宽大、可自由传输等优点，但大气湍流对其通信性能有较大的影响[1]。副载波强度调制与基带调制相比，是一种可以有效抑制大气湍流影响的光调制技术[2]。近年来国内外研究者针对副载波强度调制开展了一系列研究[3-5]。Kosti[3]用傅里叶级数法FSM（FSM，Fourier series method）推导了在Nakagami衰落信道下M-CPSK（M-ary coherent phase shift keying）系统接收信号的概率密度分布函数，分析了系统的误符号率性能。Song等[4]采用幂级数法分析了副载波DPSK（phase shift keying）调制无线光通信系统在Gamma-Gamma大气湍流信道下的误码率特性。Prabu等[5]采用MeijerG函数分析了强大气湍流下不同调制方式的无线光通信系统通信性能。

在无线光通信系统中，相位噪声主要来源于激光器相位抖动、接收端本地振荡器输出相位的时变波动、克尔效应导致的非线性相位噪声[6-7]、大气湍流折射率起伏引起的相位起伏等。相位噪声能够导致接收信号时星座图相位旋转，解调时符号误判，使系统性能劣化。对于相位调制信号，接收端解调模块内本地振荡器所产生的相位噪声将直接影响信号解调性能。席丽霞等[8]对光相位调制传输系统中相位噪声的概率分布特性进行了研究。Ragheb等[9]研究了不同线宽激光器产生的相位噪声及其MQAM调制误码率和星座图的影响。唐英杰等[10]针对大线宽和高阶QAMCO-OFDM系统的相位噪声提出了一种基于时域和频域扩展卡尔曼滤波的联合估计算法进行相位噪声补偿。而本文针对无线光副载波多进制相移键控调制系统，研究了解调模块的相位噪声对无线光通信系统差错性能的影响，基于MeijerG函数推导了Malaga大气湍流信道下接收端信号相位的概率密度函数和傅里叶级数，给出了相位噪声影响下系统平均误符号率的渐进表达式，仿真分析了光强起伏方差、相位噪声以及调制阶数对系统差错性能的影响。

2 系统模型

无线光通信系统采用副载波调制可以有效抑制大气湍流光强起伏对通信性能的影响[2]。图1所示为采用多进制相移键控（MPSK，multiple phase shift keying）副载波调制的无线光通信系统框图。

2.1 Malaga大气湍流信道模型

Malaga大气湍流信道模型是一种可以描述多种湍流分布的通用模型。对于Malaga分布，其概率密度函数如式(1)所示[11]。

其中，

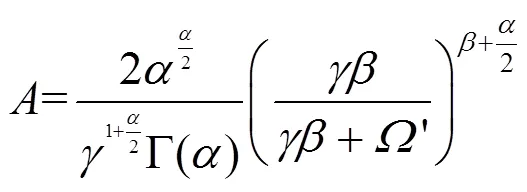
式(1)中，为湍流信道光强；为正实参数，与散射过程中大尺度涡旋的有效数目有关；为自然数，表示衰落参数的数量；()为阶第二类修正贝塞尔函数；参数为相干平均光功率；和φ分别为大气湍流信道中光波视距传播分量（LOS）与光波视距传播耦合分量（couple to LOS）的相位[12]。对Malaga分布的光强概率密度函数设置相应的和等参数，可以得到log-normal分布模型、Gamma-Gamma分布模型以及K分布模型等大气湍流信道模型。表1给出描述这3种分布的Malaga大气湍流信道模型中相对应的参数设置。

图1 无线光副载波多进制相移键控调制系统

表1 Malaga大气湍流信道模型参数设置

无线光通信系统内的瞬时电信噪比可以定义为=()2/0，而平均电信噪比则表示为([])20。因此，由式(1)可知，Malaga大气湍流信道瞬时信噪比的概率密度函数为

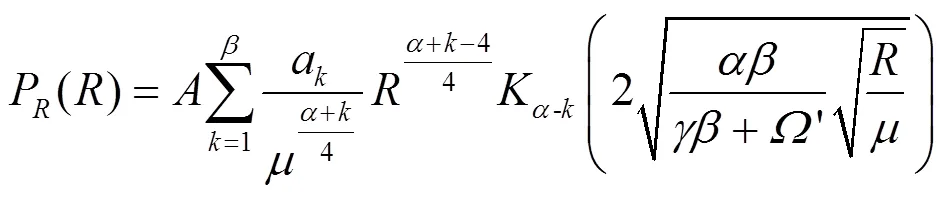
由MeijerG函数和贝塞尔函数的性质可知

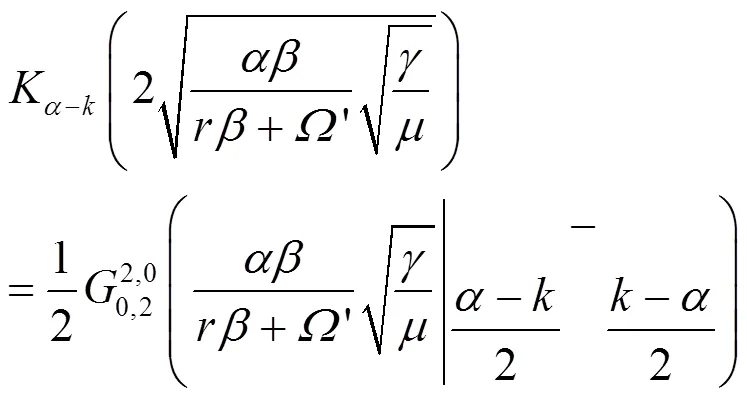
将式(3)代入式(2)，可得到MeijerG函数表示的概率密度函数

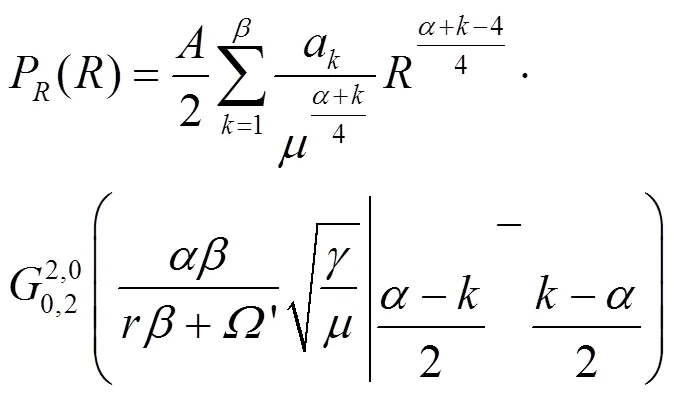
2.2 相位噪声模型

接收端光信号通过光电探测器转换为电信号，与本地振荡器输出信号相乘得到中频信号后进行相干解调。本地振荡器输出信号相位会随时间波动而产生相位起伏，这种相位起伏噪声会严重影响副载波信号的解调，导致系统性能劣化。

本地振荡器产生的相位噪声服从Tikhonov分布，其概率密度函数[13-14]为

其中，2为相位噪声方差，I()为阶的第一类变形贝塞尔函数。

由Jacobi-Anger公式[15]可将式(5)中的分子转化为

将式(6)代入式(5)中，可以用傅里叶级数表示相位噪声概率密度函数为

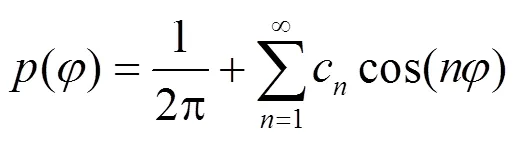
3 Malaga大气湍流与相位噪声下系统差错性能

3.1 湍流信道下接收信号相位的傅里叶级数

Malaga大气湍流信道下无线光副载波MPSK系统接收端接收信号相位设为，则其概率密度函数的傅里叶级数可以表示为[4]

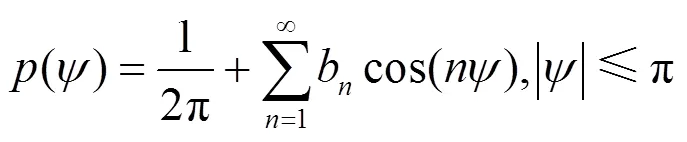
其中，b为Malaga大气湍流信道下接收信号相位的傅里叶系数。

为求得系数b，将接收信号相位表示为

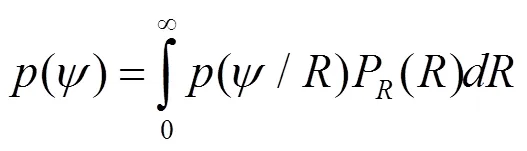
其中，P()为Malaga大气湍流信道瞬时信噪比的概率密度函数；()为Malaga大气湍流信道下接收信号相位的条件概率密度函数，它的傅里叶级数[3]为

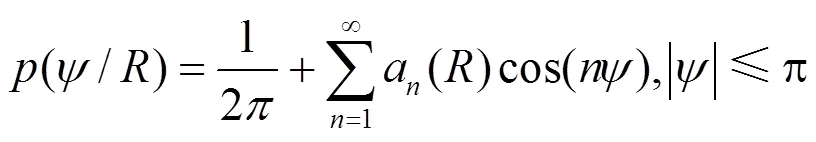
其中，傅里叶系数a()为

其中，Γ()为Gamma函数，11()为合流超几何函数。

将式(4)、式(10)、式(11)代入式(9)中，则接收信号的相位的概率密度函数为

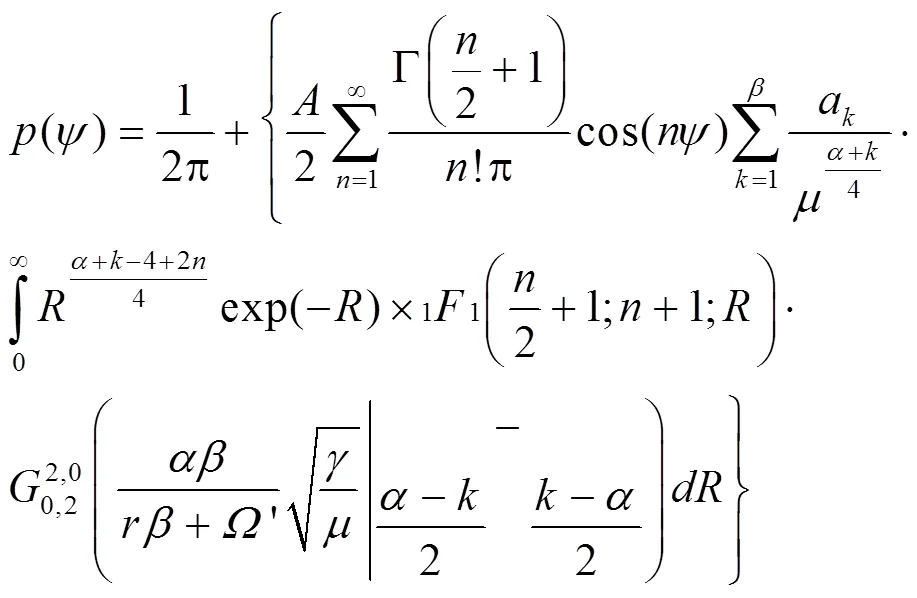
式(12)中指数函数与合流超几何函数的乘积可由MeijerG函数和Gamma函数的性质转换为

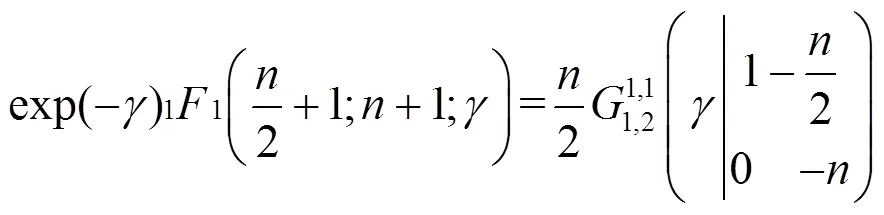
将式(13)代入式(12)式中，可得

由MeijerG函数积分性质可将式(14)转换为

对比式(8)和式(15)，可得到Malaga大气湍流信道下接收信号相位的傅里叶系数b为

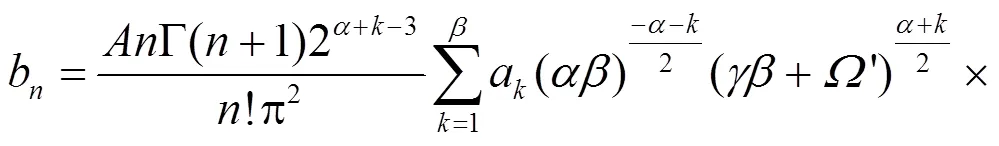
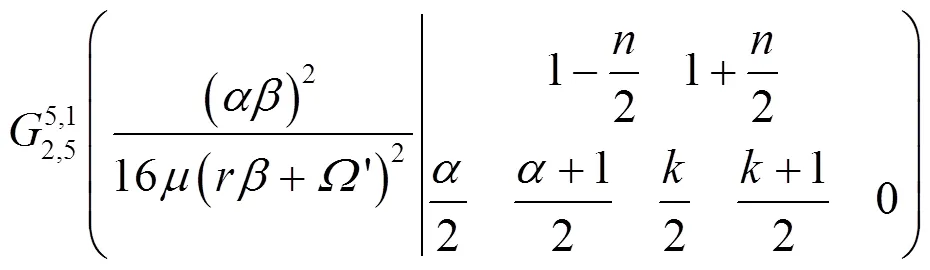
3.2 平均误符号率

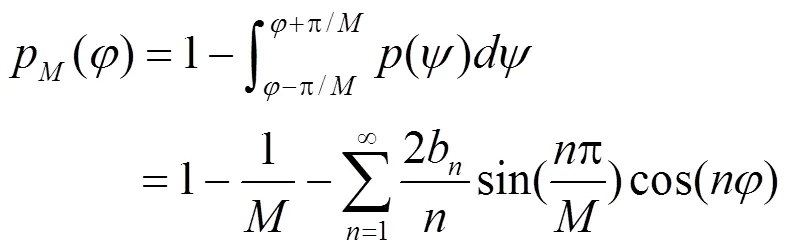
相位噪声服从Tikhonov分布且其概率密度函数见式(7)。考虑接收端相位噪声对无线光副载波MPSK系统性能的影响，由式(7)和式(17)可得到在Malaga大气湍流信道下受相位噪声影响的系统平均误符号率为

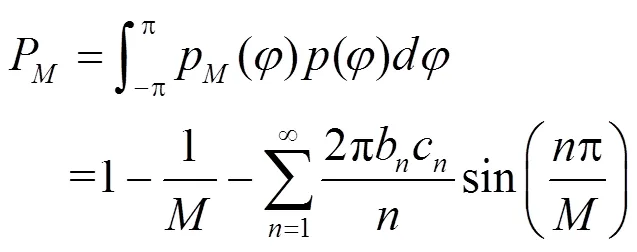
其中，c与b表达式分别见式(7)与式(16)。

4 数值仿真分析

4.1 Malaga大气湍流信道和相位噪声对无线光QPSK调制星座图影响

在高斯白噪声、大气湍流和相位噪声影响下无线光副载波QPSK信号星座图如图2所示，其中加性高斯白噪声信道=35 dB，大气湍流信道参数=11，=10，2=0.2（见表1），相位噪声标准差取σ=10°。由图2可看出，加性高斯白噪声信道下星座图中采样点在QPSK 4个相位点周围弥散分布；在Malaga大气弱湍流信道下，星座图中采样点径向拉伸，呈杏仁状；而在相位噪声影响下，QPSK调制4个相位发生明显旋转。

4.2 系统差错性能分析

图3是在平均电信噪比=25 dB和=45 dB，且Gamma-Gamma分布下，副载波调制阶数和相位噪声标准差σ对系统误符号率的影响关系。由图3可以看出，当平均电信噪比一定时，随着相位噪声标准差增大，系统误符号率增加；但在相位噪声标准差较小时，系统误符号率保持不变。这是因为此时MPSK信号星座点在相位噪声影响下开始旋转，但仍处在它的判决区域内，所以系统误符号率保持不变。此外，调制阶数越高，误符号率越大，这是由于调制阶数越高，星座图中星座点之间的欧式距离越小，在相位噪声的影响下，更容易偏离出其所在的判决区域，造成星座点之间的混叠，从而影响系统误符号率性能。由图3还可看出调制阶数越大，误符号率突然增大时所对应的相位噪声标准差越小，这说明调制阶数越高的系统，越容易受相位噪声的影响。

图2 无线光副载波QPSK调制系统星座图

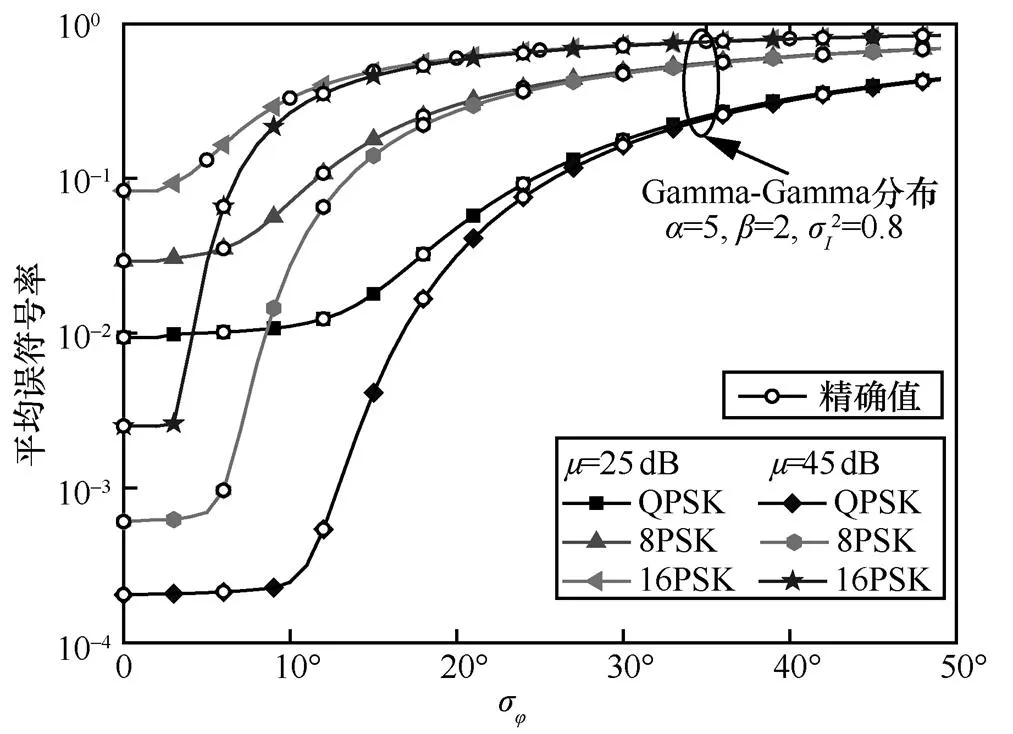
图3 相位噪声对无线光副载波MPSK系统误符号率的影响

图4为在Malaga大气湍流信道描述的不同分布下，相位噪声对无线光副载波QPSK系统误符号率性能的影响。由图3可知，当σ>10°时，QPSK系统误符号率突然增大，即其噪声容限为10°，因此在图4仿真时相位噪声标准差取5°~20°。由图4可知，当平均电信噪比=35 dB且相位噪声标准差σ=5°时，误符号率在Gamma-Gamma分布下为1.39×10−3，在K分布下为2.26×10−2。当相位噪声增加到σ=20°时，在Gamma-Gamma分布与K分布下，系统的误符号率分别增大到3.41×10−2和5.82×10−2，说明在同一平均电信噪比下，随着相位噪声标准差增大，系统误符号率也增大。

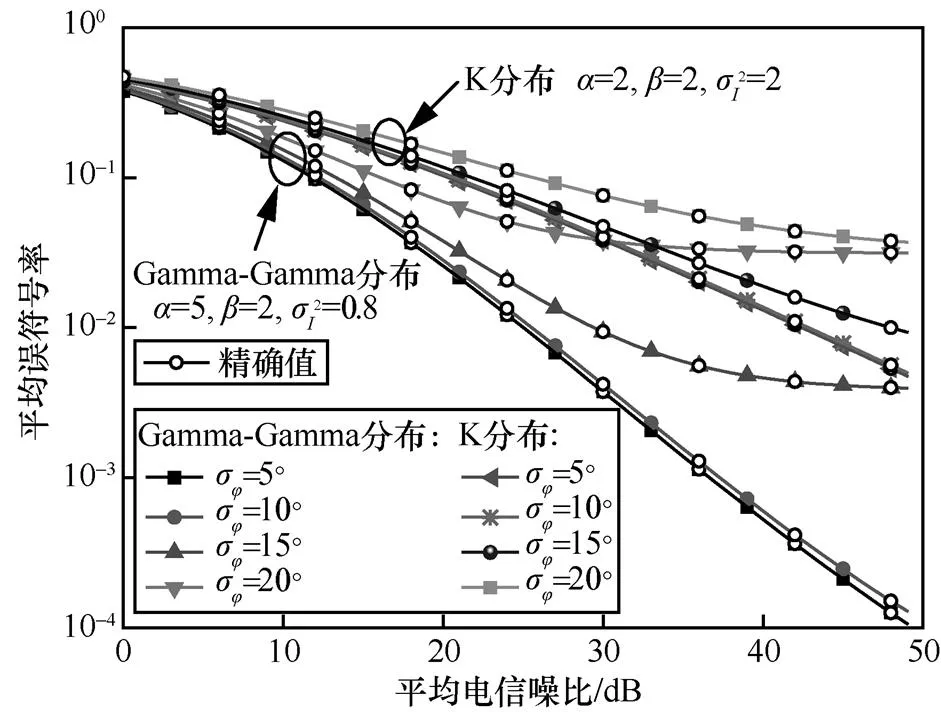
图4 Malaga大气湍流信道与不同相位噪声标准差下的QPSK系统误符号率

此外，随着平均电信噪比逐渐增大，误符号率曲线的下降趋势趋于平缓，出现系统误符号率平层，而且相位噪声标准差越大，误符号率平层出现时所对应的系统平均电信噪比越低。σ=15°时误符号率平层出现时所对应的平均电信噪比约33 dB，这说明在相位噪声标准差比较小的情况下，通过增加平均电信噪比可以减小系统误符号率，而当相位噪声标准差过大时，增加电信噪比也不能改善系统的误符号率了。

图5是在Malaga大气湍流信道所描述的Gamma-Gamma分布下，相位噪声标准差一定时，在不同的光强对数振幅起伏方差下，无线光QPSK调制系统的误符号率曲线。由图5可知，σ=5°时，随着湍流强度的增大误符号率增大，但没有出现误符号率平层，而相位噪声增大到σ=15°时，出现误符号率平层，说明误符号率平层主要是由相位噪声造成的。

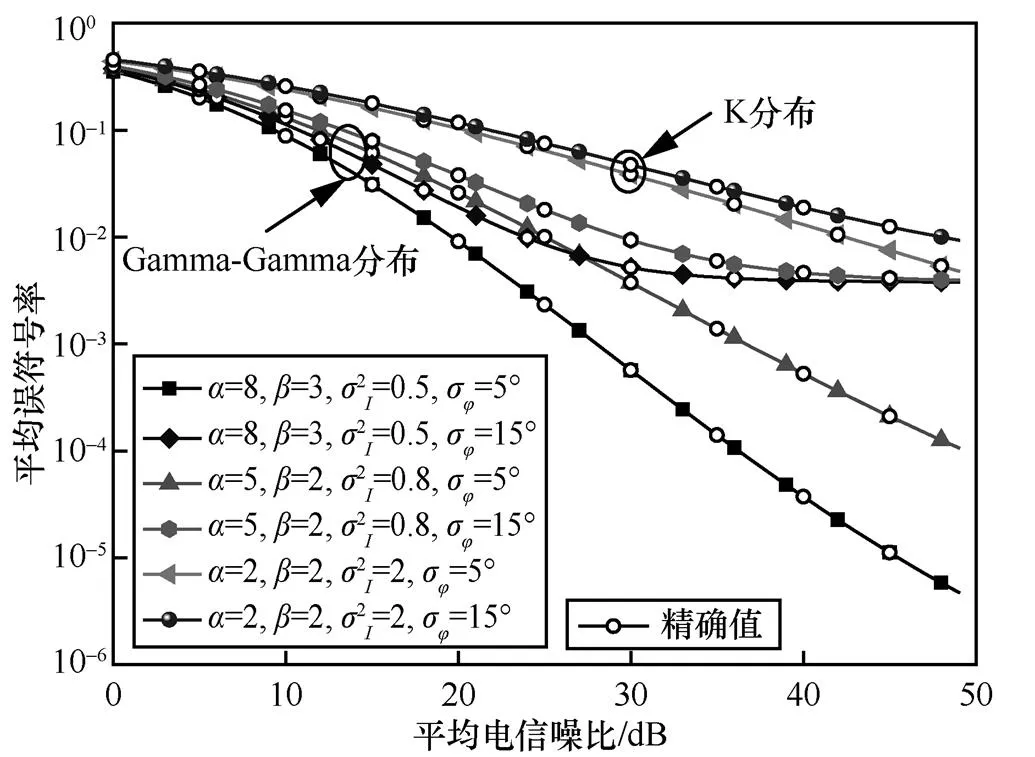
图5 不同湍流强度下系统的误符号率曲线

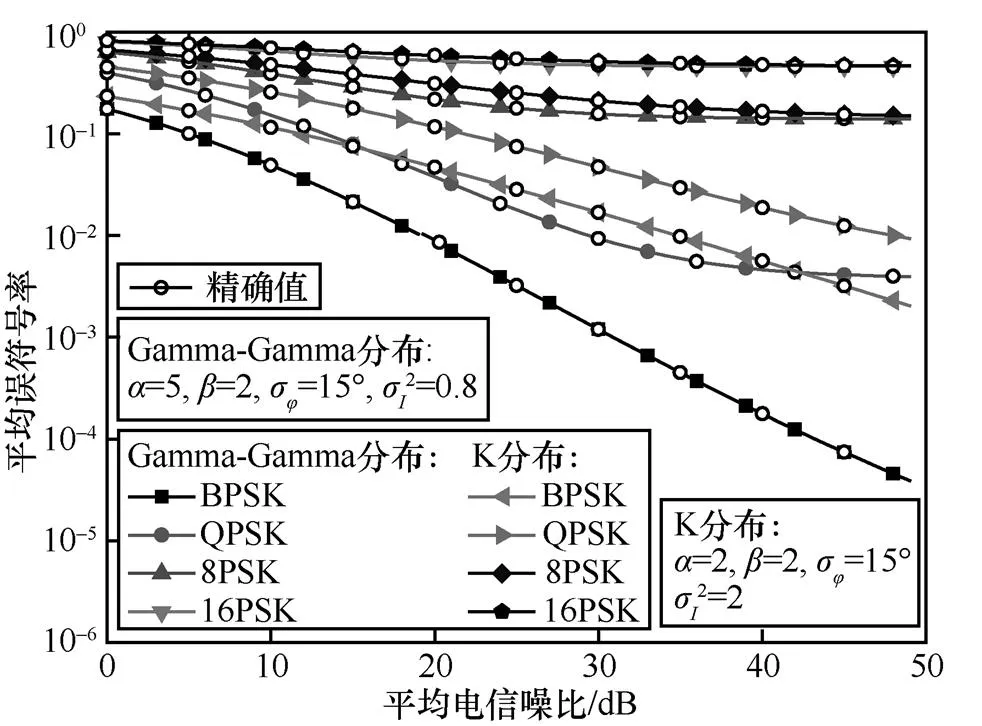
图6 不同光强振幅起伏方差下MPSK调制阶数对系统误符号率的影响

5 结束语

本文研究了在Malaga大气湍流信道下相位噪声对无线光副载波MPSK调制系统性能的影响。基于傅里叶级数及MeijerG函数性质，给出了Malaga大气湍流模型瞬时信噪比的概率密度函数，推导了Malaga大气湍流信道下接收信号相位的傅里叶级数，并得到受相位噪声影响的无线光副载波MPSK调制系统误符号率渐进表达式。数值与仿真结果表明，相位噪声较小时，系统误符号率随光强起伏方差增大而增大，当相位噪声较大时，误符号率平层的出现受调制阶数的影响大于受湍流强度的影响，而且在一定相位噪声标准差下，随着调制阶数的升高，误符号率平层出现时所对应的平均电信噪比越低。此外，数值计算结果与仿真结果曲线重合，也验证了推导的误符号率渐进表达式的准确性，研究结果对无线光副载波调制光通信系统相位噪声补偿的研究提供了一定的理论基础。

[1] MALIK A, SINGH P. Free space optics: current applications and future challenges[J]. International Journal of Optics, 2015(6):1-7.

[2] 陈丹, 柯熙政. 基于turbo码的无线光通信副载波误码性能分析[J]. 光学学报, 2010, 30(10):2859-2863.

CHEN D, KE X Z. Analysis on error rate of wireless optical communication using subcarrier modulation on Turbo code[J]. Acta Optica Sinica, 2010,30(10): 2859-2863.

[3] KOSTI I M. Average SEP for M-ary CPSK with noisy phase reference in Nakagami fading and Gaussian noise[J]. Transactions on Emerging Telecommunication Technologies, 2010, 18(2):109-113.

[4] SONG X, NIU M, CHENG J. Error rate of subcarrier intensity modulations for wireless optical communications[J]. IEEE Communications Letters, 2012, 16(4): 540-543.

[5] PRABU K, KUMAR D S, SRINIVAS T. Performance analysis of FSO links under strong atmospheric turbulence conditions using various modulation schemes[J]. International Journal for Light and Electron Optics, 2014, 125(19):5573-5581.

[6] 乔耀军, 杜晓, 纪越峰. 光四相相移键控传输系统中相位估计算法研究[J]. 光学学报, 2010, 30(5):1229-1233.

QIAO Y J, DU X, JI Y F. Phase estimating method in optical QPSK transmission system[J]. Acta Optica Sinica, 2010, 30(5):1229-1233.

[7] VOLYANSKIY K, CHEMBO Y K, LARGER L, et al. Contribution of laser frequency and power fluctuations to the microwave phase noise of optoelectronic oscillators[J]. Journal of Lightwave Technology, 2010, 28(18):2730-2735.

[8] 席丽霞, 王少康, 张晓光. 光相位调制传输系统中相位噪声的概率分布特性[J]. 光学学报, 2010, 30(12): 3408-3412.

Xi L X, WANG S K, ZHANG X G. probability density of phase noise in optical phase-modulated transmission systems[J]. Acta Optica Sinica, 2010, 30(12): 3408-3412.

[9] RAGHEB A M, FATHALLAH H. Experimental investigation of the laser phase noise effect on next generation high order MQAM optical transmission[C]//International Conference on Information and Communication Technology Research. 2015: 168-170.

[10] 唐英杰, 董月军, 任宏亮, 等.基于时频域卡尔曼滤波的CO-OFDM系统相位噪声补偿算法[J]. 光学学报, 2017, 37(9): 0906002-1.

TANG Y J, DONG Y J, REN H L, et al. Phase noise compensation algorithm based on Kalman filtering in time and frequency domains for CO-OFDM system[J]. Acta Optica Sinica, 2017, 37(9): 0906002.

[11] ANSARI I S, YILMAZ F, ALOUINI M S. Performance analysis of free-space optical links over Malaga (M) turbulence channels with pointing errors[J]. IEEE Transactions on Wireless Communications, 2015, 15(1): 91-102.

[12] 陈丹, 雷雨, 柯熙政. 无线光自适应副载波MDPSK调制系统特性分析[J].电子学报,2018,46(07):1748-1753.

CHEN D, LEI Y, KE X Z. Performance analysis of wireless optical adaptive subcarrier MDPSK modulation system[J]. Acta Electronica sinica, 2018,46(07):1748-1753.

[13] KHALIGHI M A, UYSAL M. Survey on free space optical communication: a communication theory perspective[J]. Communications Surveys & Tutorials IEEE, 2014, 16(4):2231-2258.

[14] NIU M, CHENG J, HOLZMAN J F. Error rate analysis of M-ary coherent free-space optical communication systems with K-distributed turbulence[J]. IEEE Transactions on Communications, 2011, 59(3): 664-668.

[15] ABRAMOWITZ M, STEGUN I A, MILLER D. Handbook of mathematical functions with formulas, graphs and mathematical tables (national bureau of standards applied mathematics series No.55)[J]. Journal of Applied Mechanics, 1965, 32(1):239.

Effects of phase noise on subcarrier modulation performance over Malaga turbulence channel

KE Xizheng, WANG Chenhao, CHEN Dan

School of Automation & Information, Xi’an University of Technology, Xi’an 710048,China

The performance of wireless optical system employing subcarrier phase-shift keying modulation was researched, which was influenced by phase noise of system demodulator under on Malaga atmospheric turbulence channel. Combined Fourier series and MeijerG function properties, the probability density function of instantaneous signal to noise ratio in the Malaga turbulence model was got. The Fourier series of receiving signal phase and the closed form expression of symbol error probability were derived, which were in the wireless optical subcarrier shift keying modulation system. Under different modulation order and light intensity fluctuation variance,the influence of phase noise on the system symbol error rate was analyzed. The numeric results present that the system symbol error rate increases with the light intensity fluctuation variance when the phase noise is lower. When the phase noise is larger, the influence of modulation order is greater than of turbulence intensity to the error-rate floor appearing. And with the increasing of modulation order, the corresponding average signal to noise is lower when symbol error-rate floor appears.

wireless optical communication, Malaga turbulence distribution, subcarrier modulation, phase noise, average symbol error probability

TN929.1

A

10.11959/j.issn.1000−436x.2018236

柯熙政（1962−），男，陕西临潼人，博士，西安理工大学教授、博士生导师，主要研究方向为无线激光通信及先进导航理论与技术。

王晨昊（1993−），男，陕西汉中人，西安理工大学硕士生，主要研究方向为无线激光通信及信号及现代信号处理。

陈丹（1975−），女，陕西汉中人，博士，西安理工大学副教授、硕士生导师，主要研究方向为无线激光通信及现代信号处理。

2018−03−22；

2018−07−06

国家自然科学基金资助项目（No.61671375）；陕西省科技计划资助项目（No.2016GY-082）；陕西省重点产业创新项目资助项目（No.2017ZDCXL-GY-06-01）

The National Natural Science Foundation of China(No.61671375), Supported the Industrial Research of Science and Technology Plan of Shannxi Province(No.2016GY-082), Innovation Projects of Key Industries of Shannxi Province(No.2017ZDCXL-GY-06-01)