供水不足地区园艺植物类温室自动灌溉系统的设计与试验

国俊保， 高爱玲

(潍坊科技学院，山东寿光 62700)

随着全球气候变暖的加剧，水资源日益减少，农业生产过程中须要消耗大量的水资源，因此，提高农业生产过程中水资源利用率成为了当前农业领域的研究重点[1]。在我国西北地区，大量区域目前仍处于水资源匮乏状态，所以适用于水资源紧缺情况的温室灌溉系统是一个有实际意义的研究内容[2]。并且我国西南部区域时而发生旱灾，如果能够设计出水资源紧缺情况的温室灌溉系统，则能够帮助旱灾地区减少经济损失[3]。

许多研究人员采用人工智能技术与机器学习技术对温室的历史数据进行学习，使用训练获得的模型预测温室内植物未来的变化趋势[4-5]。在温室供水充足的情况下，温室内微气候的变化趋势较为稳定，所以人工智能与机器学习训练的模型能够准确地预测温室内植物参数的变化趋势。但是如果发生突发性旱灾，采用人工智能或者机器学习技术则难以获得理想的预测与控制效果。

计算流体力学能够有效地模拟各种流场的过程[6]，温室中土壤-植物-空气的水分交换过程是一种典型的流场过程[7]，并且计算流体力学不须要通过对历史数据的学习即可建立模型，因此计算流体力学建立的预测模型实时性较高，能够随着问题的实时变化而自适应地改变模型的参数，从而能够应对一些突发性状况的发生。

为了在不影响植物蒸腾速率的前提下降低灌溉的水量，采用计算流体力学对温室微气候、 植物活动参数与土壤基质参数均进行建模与预测， 该模型考虑了土壤-植物-空气水

分交换过程的各个环节，并且能够仿真出温室内蒸腾速率与微气候的变化过程。

1 材料与方法

1.1 试验环境与方法

试验于2017年6月在山东省潍坊地区10 m×10 m的Venlo型玻璃温室进行。温室由4 mm厚的园景玻璃构成，在屋脊两侧装备了连续的屋顶通风口，通风口在室外温度超过20 ℃的时候打开，一般通风口在白天打开，在夜晚关闭。为了防止温室温度过高，采用1个遮阳幕，遮阳幕的成分为铝(16%)与聚乙烯(84%)，导热率为0.15 W/mK，透射率为50%。温室地面为混凝土，地面放置4个架子(3 m×1.5 m)，架子高度为0.8 m，水仙花花盆均匀地放置于4个架子上，花盆容积为0.74 L，高度为8.7 cm，花盆内填充均匀分布的泥炭，密度为0.12 g/cm3。

架子上植物的冠层面积约为18 m2，叶面积指数(leaf area index，LAI)为2.36，植物密度为15盆/m2，植物平均高度为24 cm。每天使用滴灌设备为每盆植物浇灌2次完全营养液，其中3个架子的植物进行供水充足的试验，这些花盆中泥炭的水势保持在-2 kPa以上；第4个架子的植物进行供水不足的试验，周期性地停止灌溉，使其处于供水不足的状态。

1.2 温室微气候的数据采集

使用传感器采集温室内的微气候数据。试验温室的总体结构如图1所示，使用温度传感器(T)与湿度传感器(R)测量空气的温度与相对湿度，传感器分别放于3个位置：植物上方15 cm处(T1，RH1)，植物内部(T2，RH2)，架子下方(T3，RH3)。此外测量叶片的温度(TI)，在地面放置PT100铂探针，测量架子下方的地面温度。使用CNR4型净全辐射传感器采集辐射的长波、短波数据，在1.29 m的高度放置1个热球式电风速计，测量冠层的气流速度。每隔3 s采集1次上述所有参数数据，每隔10 min将数据保存至数据库中。

1.3 基质栽培的参数

在6个花盆中埋了负压计与含水量传感器，分别测量花盆的泥炭基质势ψ(kPa)与含水量θ(体积分数)，其中3个花盆为供水充足的花盆，另外3个为供水不足的花盆。每隔3 s采集1次上述所有参数数据，每隔10 min将数据保存至数据库中。

1.4 植物活动的数据

通过有孔石膏在6张植物叶片下面固定Cu-Cs热电偶，每隔3 s测量1次6张叶片的温度，将10 min总数据的平均值作为结果保存至数据库中。使用气孔计测量叶片的气孔阻力。在冠层的中间放置1个高分辨率Melter-Toledo电子秤，测量冠层蒸腾所流失的水量，电子秤的托盘(56 cm×56 cm)保持水平，每隔1 h记录花盆流水量。

2 建立计算流体力学(CFD)模型

为了建立计算流体力学模型，在感兴趣区域周围定义1个计算域，然后将计算域离散化为表征体元，最终求解计算域中质量(空气、水分)与能量的守恒方程量。根据文献分析[8]，温室的湍流一般位于温室的高处，为了记录湍流的运动变化，将变量分为1个平均分量与1个波动分量，并且将等式平均化处理，获得RANS等式(雷诺平均等式)。

使用ANSYS Fluent 15.0流体计算软件仿真CFD模型，该软件使用有限体积法求解二维非稳态对流扩散方程。

2.1 模型的基础方程

因为温室中连续通风口的主风向一般垂直于通风口，则气流的二维平面垂直于屋脊，因此模型仅须要考虑二维的情况。二维湍流动能输运方程的一般形式为

(1)

式中：Φ表示非量纲输运量的集合，即动量、质量与能量；U与V是速度向量的元素；Γ是扩散系数；SΦ是输运方程的源项(source term)。将k-ε湍流模型设为多组分湍流封闭模型，因为空气密度(ρ)不仅依赖温度还依赖空气的含水量，所以无法应用Boussinesq模型。将空气密度定义为一个关于温度与质量的函数：

(2)

式中：T是局部温度，K；R是理想气体常数，R=8.31 J/(mol·K)；Pop为工作压力，Pa；ωi是组分i的质量值；Mi为组分i的分子量，kg/mol。

2.2 辐射子模型

为了区分辐射中短波(0.1～3 μm)与长波(3～100 μm)的贡献度，设计了一个辐射子模型。对于有限数量的离散立体角，可用式(3)求解单色亮度方程，每个离散立体角对应的向量方向为

(3)

聚集整个空间的每个单色亮度，即可获得全局的辐射通量qs，表示为

(4)

热平衡中每个单位体积的辐射贡献度是能量守恒方程的一个源项(source term)，表示了辐射qs(s)的散度。

(5)

在当前的研究中，短波长与长波长之间存在差异[9]。与短波辐射相比，冠层吸收长波辐射的量可忽略不计，在白天冠层吸收的长波辐射小于短波辐射的4%。

2.3 植物子模型

2.3.1 多孔介质 将植物抽象为均匀分布的多孔介质，该多孔介质对气流具有阻力(对应植物的气孔阻力)，表示为能量守恒方程中的一个源项SΦ。根据Darcy-Forchheimer方程，植物每个单位体积的拉力可表示为黏性丢失项与内部丢失项2个项的总和，如下式所示。

(6)

式中：K是多孔介质的渗透性，%；CF是非线性动量的衰减系数；ρa是空气密度，kg/m3；μ是空气的动态黏度，(N·s)/m2；V是空气的速度值，m/s。根据文献[10]分析，实际的空气动态黏度非常低，是10-5(N·s)/m2数量级，所以可以忽略式(6)的第1项，可得：

(7)

式中：LAD是叶密度，定义为LAI/冠层高度(H)；CD是拉力系数。

从式(7)可以看出，仅须要获得CD值即可求解植物每个单位体积的拉力，凤仙花的CD值约为0.32。

2.3.2 能量平衡模型 冠层的太阳辐射为Rg，植物通过蒸腾作用以及与周围空气的热交换进行能量传递，假设蒸腾作用的热通量密度为Trd，周围空气的热通量密度为Qs。最终，叶片的能量平衡公式写为

Rgabs-Trd-Qs=0。

(8)

可根据Beer法则[式(9)]直接推导出冠层每个细胞吸收的辐射量Rgabs，W/m2：

Rg(y)=Rg0exp[-KcLAD(H-y)]；

(9)

Rgabs=Rg(yi)-Rg(yi+1)。

(10)

式中：yi与yi+1分别是细胞i的上一坐标与下一坐标。Rg0是冠层上的全局辐射，W/m2；Kc是辐射的消光系数；供水充足的情况下该值为0.95，供水不足的情况下该值为0.64，这2个值是使用式(9)计算冠层上面与下面的短波辐射而来。这个差值的原因是在植物缺水的情况下，植物的叶片会自动地旋转，这个生理机制能够降低植物吸收的太阳辐射量，因此降低了蒸腾作用。

冠层的可感知热量定义为

Qs=2LADρaCp[(TI-Ta)/Ra]。

(11)

式中：ρa是空气密度，kg/m3；Cp是指定压强对应的空气热量，J/(kg·K)；TI与Ta分别是叶片与空气的温度。

一个给定区域的潜热密度定义为

(12)

式中：γ是温湿常数；VPDa是空气的饱和水汽压差，Pa；Δ是饱和水蒸气压曲线的斜率；根据文献[11]，将气动阻力Ra设为一个常量，Ra=271 s/m。Rs是气孔阻力，s/m，采用FFD(全因子试验设计)[12]方法可推导出Rs，表示为

Rs=(-115×rg-139×rh-39×τ+139×rg×rh+43×rg×τ+11×rh×τ+661×rg2-368×rg3)×[1+(ψ-11.41)1.05]。

(13)

式中：rg=(Rg-75)/75，rh=(RH-65)/10，τ=(T-20.5)/5.5，rg是辐射量，rh是湿度值，τ是温度因子，ψw是土壤基质势(kPa)的减少量，RH为相对湿度。将式(8)进行转换，可计算出细胞的叶片温度(TI)：

(14)

2.3.3 水平衡模型 根据文献[13]模型，可通过下式计算基质水势的减少量ψw：

(15)

式中：θres与θsat分别是土壤剩余含水量与土壤饱和含水量；α(kPa)与N是2个待校准的参数，这2个参数来自于拉力计与含水量传感器的测量数据。根据多线性拟合的结果，可获得以下参数值：θsat=0.887 cm3/cm3，θres=0.1 cm3/cm3，α=0.134 kPa-1，N=1.469。通过式(16)计算每个时间点i的含水量，式(16)定义了蒸腾作用与初始化含水量(θ0)的关系。

(16)

式中：θi是当前时间点的含水量i，cm3/cm3；θ0是初始含水量，cm3/cm3；ts是时段长度，本研究ts等于3 600 s；ss是架子的总面积；Travg，j是在时间点j时的冠层平均蒸腾速率；λ是水的潜热量，J/kg；m是植物总量(m=264 kg)；ρw是水密度，kg/m3；Vp是花盆的容积，m3。

2.3.4 模拟程序 对于动量与热量的输运方程采用二阶迎风差分格式[14]处理，提高输运方程的计算准确率。对于压力连接等式采用半隐式格式[15]来求解压力-动量方程。所有变量的收敛条件是10-6数量级。

3 模型验证

采用2个准确率性能指标评估本模型的预测准确率，分别为RMSE(均方根)与R2(确定系数)，RMSE也称为预测系统的拟合标准差，值越小表示预测越精确；R2是通过数据的变化来表征一个拟合的好坏，R2取值范围为[0，1]，越接近1，拟合效果越好。

3.1 试验结果与分析

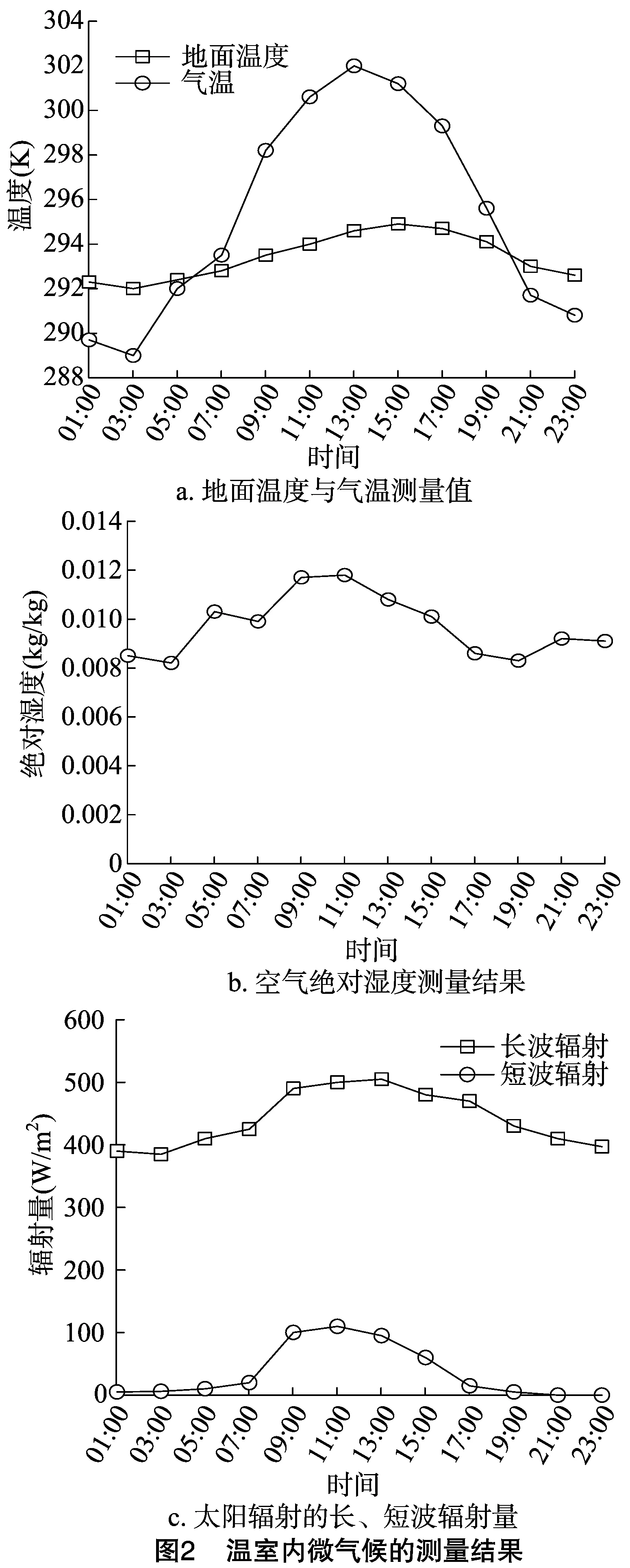
首先对供水充足与供水不足2种情况分别进行分析与研究。将二维非稳态仿真的时间步长设为2 h，周期为从6月14日01：00—23：00，从11：00—20：00打开通风口，6月14日对供水不足的花盆停止灌溉。试验中测量的数据作为预测模型的输入数据，测量的结果如图2所示。从图2可以看出，太阳辐射的变化曲线与气温、地面温度均具有相关性，在13：00达到最大值。

在6月14日01：00使用6月14日00：00的数据进行一次初步仿真，对于供水不足的情况，初步仿真结果中的初始水量为0.652 cm3/cm3，使用基于水平衡的子模型计算每个时间点的土壤基质水势。对于供水充足的情况，将土壤基质水势设为恒定值，该值固定为-1 kPa。

3.2 空气温度与湿度

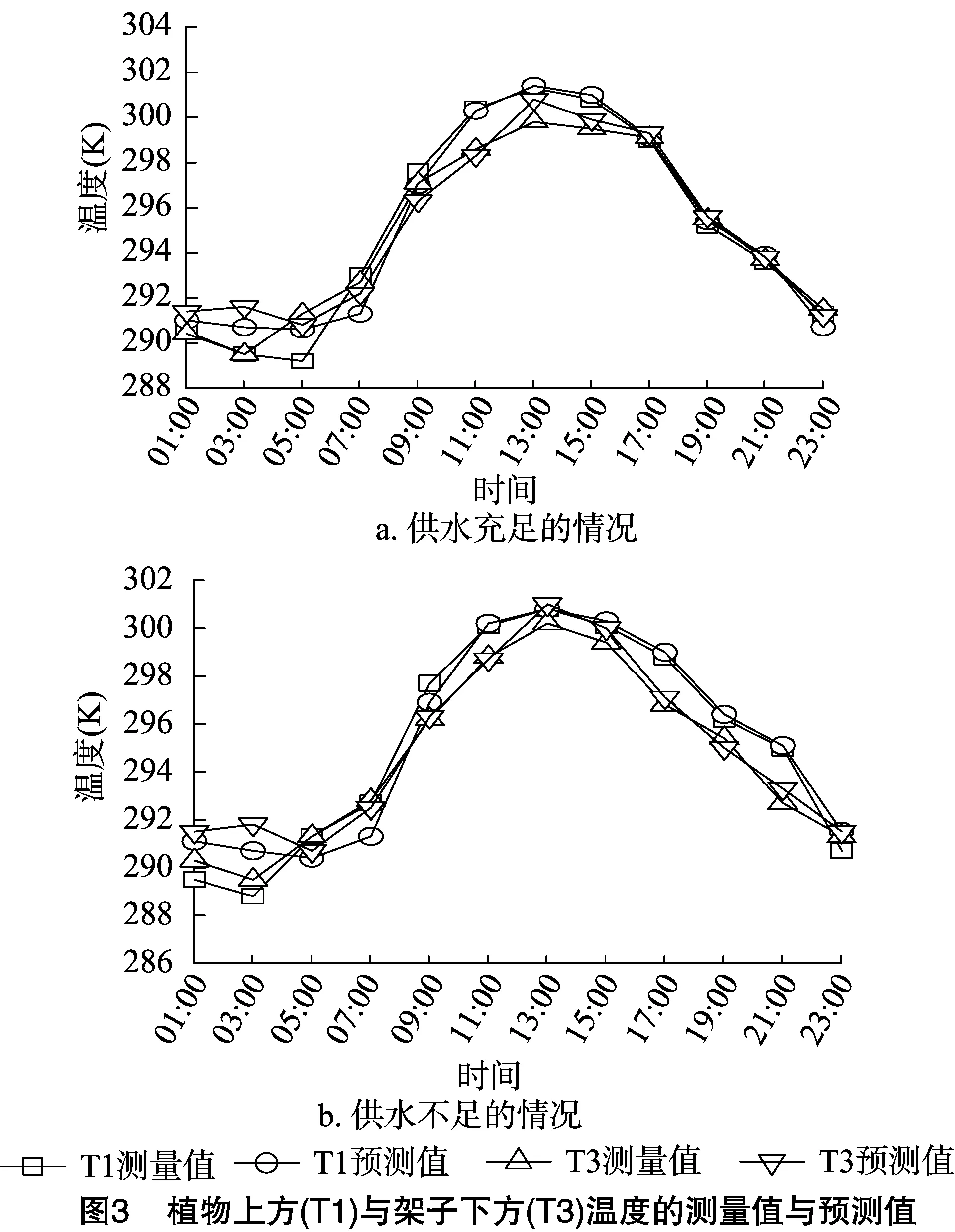
2种供水条件下3个测量位置的气温随着时间的变化曲线如图3与图4所示。气温与叶片温度的测量值与预测值表现出相同的趋势，2种供水条件下气温的预测值与测量值能够较好地拟合。由表1可以看出，对于供水充足情况，所有的结果中R2结果均大于或等于0.97，RMSE均小于或等于1.14；对于供水不足情况，所有的结果中R2结果均大于或等于0.94，RMSE均小于或等于 1.62。因为2种供水条件的温度差异较小，所以供水是否充足对观察周围温度的影响较小。2种供水条件的差异主要由初始的环境参数引起，供水不足情况的叶片温度比供水充足情况约高1K，其原因是供水不足情况的蒸腾作用减弱，而蒸腾作用能够降低叶片的温度。2种供水条件的叶片底部温度几乎相同，因为叶片底部的蒸腾作用均较弱。

此外，研究了2种供水条件下3个测量位置的相对湿度，分别表示为RH1、RH2与RH3，相对湿度随着时间的变化曲线如图5所示。对于供水充足的情况，结果显示冠层内部相对湿度的预测值与测量值高于冠层的上面与下面。对于供水不足的情况，3个位置相对湿度的测量值与预测值较为接近。总体而言，2种供水条件的预测值与测量值实现了较好的拟合。从表1可以看出，对于供水充足的情况，R2大于0.88，RMSE小于8.66；对于供水不足的情况，R2大于0.78，RMSE小于6.69。

3.3 泥炭土的基质势

在停止灌溉5 d后，统计了1 d内测量与预测的泥炭土的基质势值(图6)。因为白天植物的视觉特征较为明显，因此试验主要关注白天。因为停止了灌溉，土壤内的水量随着植物的蒸腾作用而减少。从图6可以看出，泥炭土基质势的预测值较好地拟合了测量值，并且获得了较高的预测准确率，预测性能指标分别为r2=0.99，RMSE=-3.38。

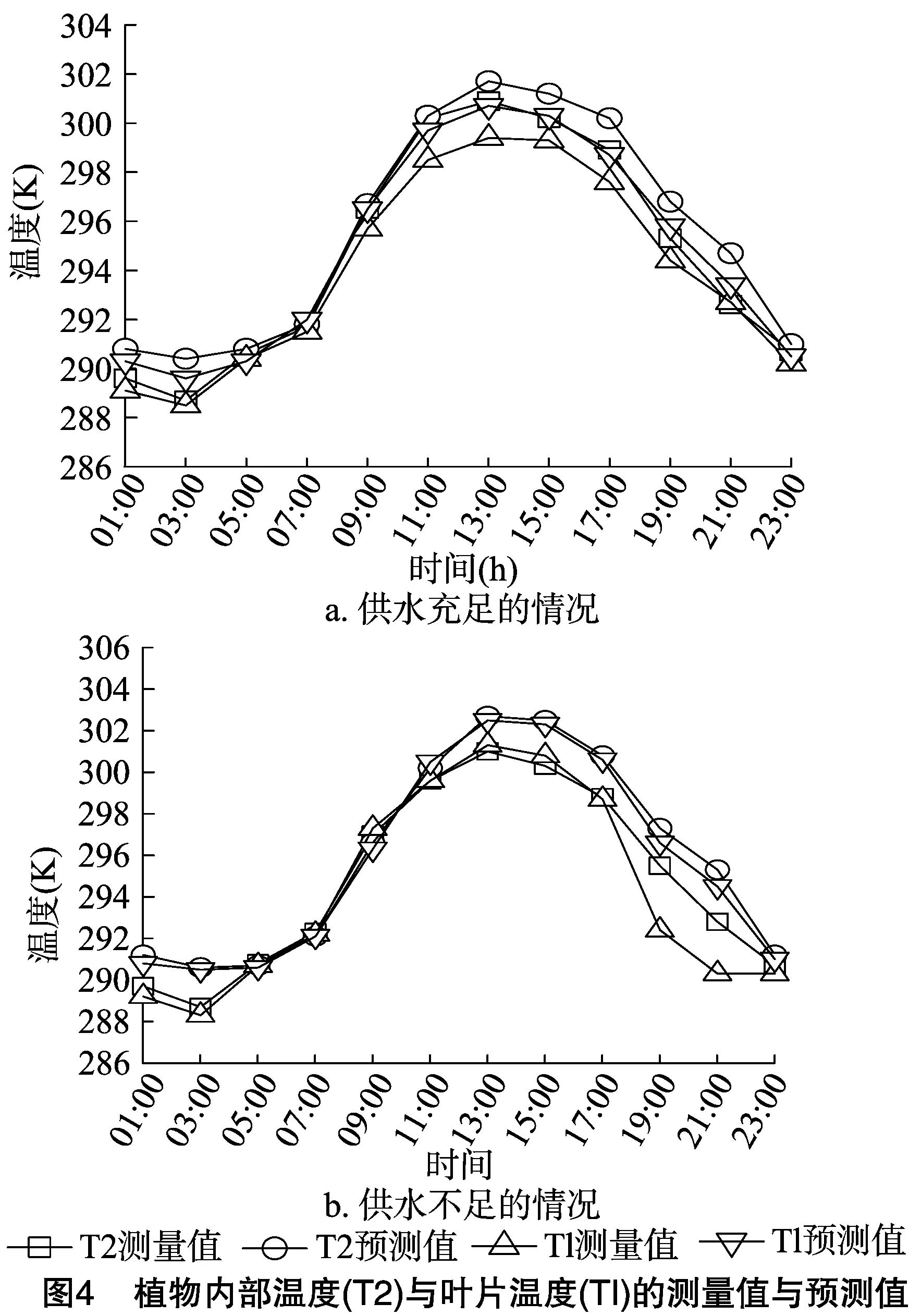
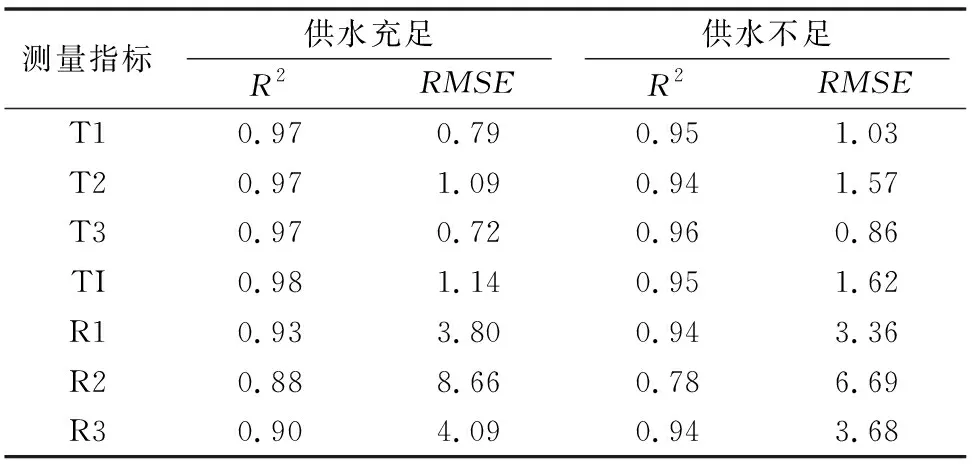
表1 温室内微气候各个参数的测量结果

3.4 观赏植物的相关参数

3.4.1 植物的气孔阻力 为了分析光照对植物气孔阻力的影响，对阴影区域叶片与光照区域叶片均进行了试验分析，供水充足与供水不足2种情况的气孔阻力变化曲线如图7所示。从图7-b可以看出，从大约10：00开始，气孔阻力开始上升，因为此时土壤基质势开始降低，植物通过增加气孔阻力来限制植物的蒸腾作用。从图7-a可以看出，供水充足情况的气孔阻力也从10:00开始上升，此时阳光辐射与空气气压差均开始上升，所以植物通过增加气孔阻力来限制植物的蒸腾作用，但其上升幅度远小于供水不足的情况。

CFD模型能够有效地预测出阴影区域叶片与光照区域叶片的气孔阻力变化曲线，供水充足情况的预测性能指标为r2>0.4，RMSE<168；供水不足情况的预测性能指标为r2>0.51，RMSE<527。

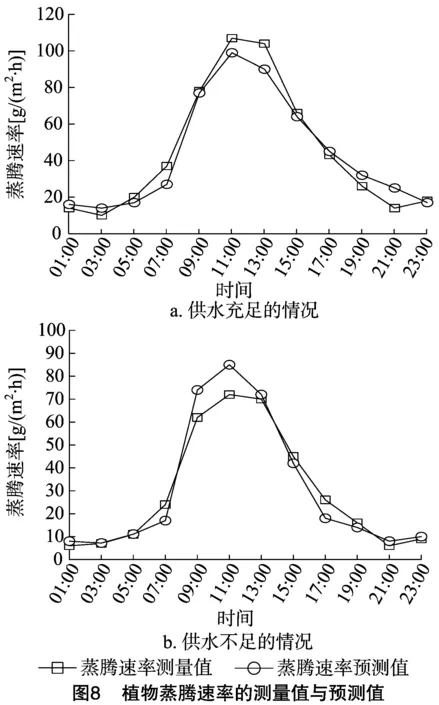
3.4.2 植物的蒸腾速率 供水充足与供水不足2种情况的植物蒸腾速率变化曲线如图8所示。供水不足情况的蒸腾速率小于供水充足情况。供水不足情况的蒸腾速率最小测量值为1.43 g/(m2·h)，低于供水充足情况的最小蒸腾速率。总体而言，本模型能够有效地预测供水充足与供水不足2种情况的植物蒸腾速率，供水充足情况的预测性能指标为r2=0.98，RMSE=5.87；供水不足情况的预测性能指标为r2=0.97，RMSE=5.64。此外，计算了24 h蒸腾速率的总预测误差，供水充足情况的总预测误差为3.32%，供水不足情况的总预测误差为4.82%。

4 结论

目前温室自动灌溉系统大多针对供水充足的稳定环境，为了提高供水不足情况的灌溉效率，设计了一种采用物联网的园艺植物类温室自动灌溉系统。为了在不影响植物蒸腾速率的前提下降低灌溉的水量，采用计算流体力学对温室微气候、植物活动参数与土壤环境参数均进行建模与预测，该模型考虑了土壤-植物-空气水分交换过程的各个环节，并且能够仿真出温室内蒸腾速率与微气候的变化过程。在山东潍坊地区采用水仙花盆景进行了试验，对供水充足与供水不足2种情况均进行了试验，该模型对温室微气候、植物活动参数与泥炭土基质势均获得了准确的预测效果。