基于路径加权的军事通信网波动性评估算法

孙 浩，蔡晓霞，陈 红

（国防科技大学电子对抗学院，合肥 230000）

0 引言

目前已经迎来了一个信息化时代，美国海军主张要从过去以平台为中心的战争向以网络为中心的新战争形式转变[1]。战术互联网是美军的新一代通信系统，它实现了美军三大传统通信系统的互联互通，在战场信息的传递与交互上至关重要[2]。战场上的通信网将会在未来战争中起到举足轻重的作用，国内外学者对其评估做了大量研究。近年来，随着OPNET等软件对网络业务性能仿真带来的便利性，大部分评估是针对吞吐量、丢包率等业务性能的，而对起到骨架作用的拓扑结构研究相对较少。

网络的拓扑反映了网络内部的结构，在网络中起到支撑性作用。随着网络拓扑结构设计技术呈现出的多样性，拓扑层抗毁性评估方法也多种多样。国内外研究者主要从节点或链路等角度提出了拓扑层抗毁性评估方法。文献[3]首次提出了波动性的概念，将其作为抗毁性度量值的参考指标，将网络节点间两两通信后经过某一节点的次数作为节点波动性度量值，用所有节点的波动性度量值均方差表示网络波动性评估值。该方法仅用于简单网络的评估且节点波动性度量值的定义没有考虑链路重要程度的差异。文献[4]提出了聚点团的概念，将节点与所连链路作为一个跳面，将此跳面和与之相连的链路作为下一级的跳面，通过链路与跳面的比值计算跳面节点及网络的抗毁性。该方法从宏观上评估了网络拓扑的抗毁性，但没有反应节点团之间路由数量的个体差异。文献[5-6]对节点抗毁度进行了定义，然后用节点抗毁度的均值评估网络的抗毁性，没有体现节点之间重要程度的不同。

节点波动性度量值具有较重要意义，它表示了网络拓扑中是否存在关键节点或链路。这对军事通信网极其重要，若拓扑层中存在关键链路或节点，这将是敌方首先攻击的目标。因此，应当尽量避免出现关键节点或链路，使攻击任何一个节点或链路对网络拓扑造成的损坏程度基本相同。本文对文献[3]提出的基于节点波动性的经典算法进行了改进，并应用于复杂网络波动性评估，仿真结果显示新算法在评估准确性上体现出很大的优越性。

1 传统网络波动性评估算法

1.1 评估模型

传统算法用所有节点波动性度量值的均方差评估网络波动性，定义C（k）为网络拓扑波动性度量值：

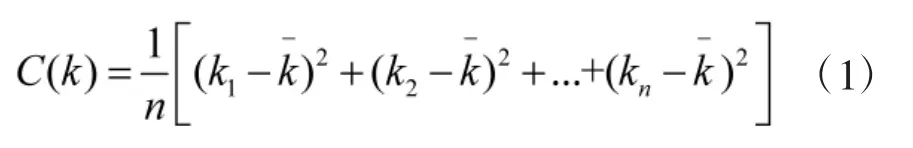
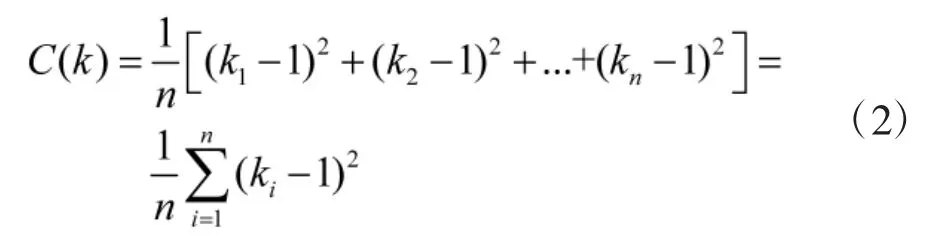
1.2 算法及其仿真

对于给定的网络拓扑图，节点波动性度量值求法如下：

1）求出所有节点两两通信（不包括待求的节点）经过待求节点的链路次数之和Ci。2）对拓扑图中所有节点，求其经过节点链路数平均值。3）对每个节点，求得对应的Ci与平均值的比值ki。4）将ki代入公式，得到整个网络的波动性度量值。

图1 C（k）=0

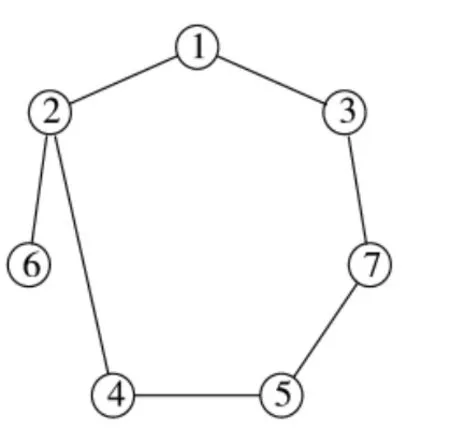
图2 C（k）=0.191

图3 C（k）=0.532

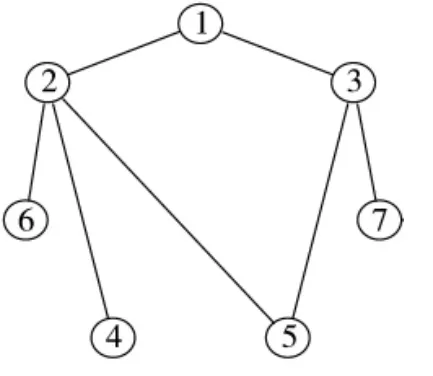
图4 C（k）=0.903

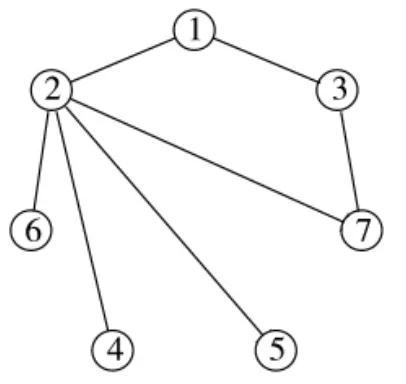
图5 C（k）=1.204

图6 C（k）=2.725

图1～图6表示了6个网络拓扑结构图。这6个拓扑结构图具有相同的链路数和节点数。用传统算法对网络进行波动性评估，评估结果如下页表1所示。

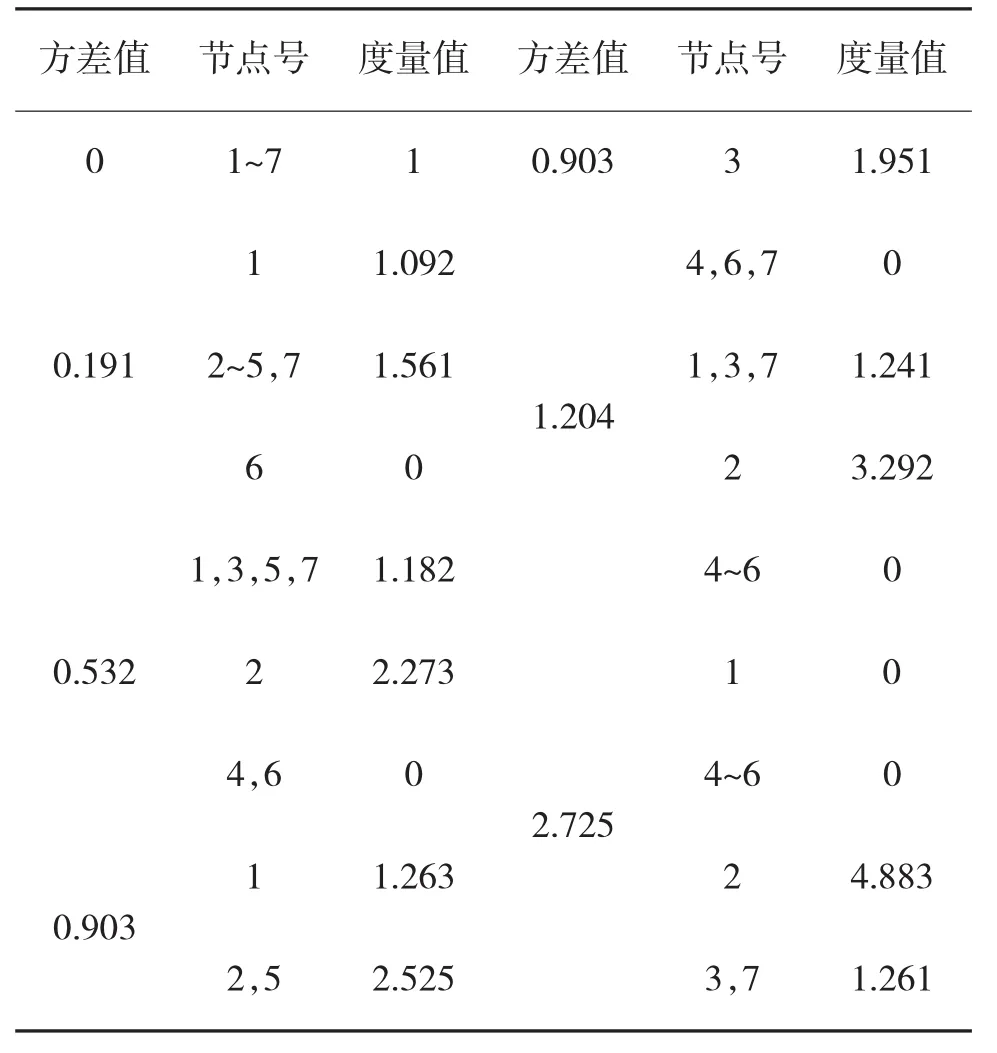
表1 传统算法得到图1～图6的网络波动性度量值

拓扑图1～图6网络波动性度量值度逐渐增大，说明网络越来越不稳定。比较这6个网络拓扑图，可以发现拓扑图1具有最好的稳定特征，图2～图6稳定性逐渐降低。图1的节点度量均方差值等于0，说明拓扑图1中所有节点的重要程度相同，不存在关键节点，这也是为保证具有良好稳定性能将网络设计成环装的原因。而图6近于星形网络，网络均方差最大，因此，星形网络抗毁性最差。所以，为使得网络具有较好的稳定性，应当将网络避免设计成星形或类似星形结构。

1.3 仿真结果分析

传统算法评估结果显示，对于简单网络，传统算法可以正确表示每个节点重要程度的高低，也能够准确评估网络波动程度。但是在节点两两通信时没有区分链路的重要程度不同，这与实际情况不相符。因为在网络实际运行中，用户间的通信会使得链路的使用率不同，使得不同的链路重要程度不同。在评估过程中应充分考虑链路重要程度的差异性，本文接下来对传统算法进行了改进。

2 对传统算法的改进

上述传统算法中，将所有节点进行两两通信，将经过与某一节点相连链路的次数作归一化处理，作为节点的波动性度量值。此计算方式存在合理性但细致性不足且实际情况不吻合。因为在不同节点对之间的通信中，迂回路由的数量不同会使每条路由的重要程度不同，进而使链路具有不同的重要性。如图7中，节点2与节点6通信，仅有g一条路由，若链路g失效则两节点不能通信，则可设链路g在此次通信中重要程度（权值）为100%，而节点2与节点3通信，可选路由有ab和cd两条，任何一条失效另一条也会保证通信正常，则此次通信中路由ab和cd应各占权值的50%。

这样在每次两节点通信中都应该突出链路重要程度的不同，进而更细致突出节点的波动性的不同，使对网络的波动性评估更科学地贴近事实。

2.1 改进的思想

每次任意两节点之间进行通信时，设其所有可选路由权值总和设为1，此权值平均分配给两节点间所有可以连通的路由。

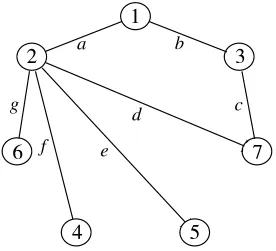
图7 将图5链路进行标注

如图7，假设节点6与节点7进行通信，可以连通的路由有gd和gabc两条，那么，此次通信中2条路由各占总权值1的1/2。因为在每条路由（gd和gabc）中，任何一条链路的故障都会导致该路由的失效，所以在两节点的通信中，任何路由中的任何链路具有相同的重要程度（均可导致一条完整路由的失效），因此，节点6与节点7的通信中，每条链路的权值应与路由权值相同均为1/2，所以链路权值分配为：gd路由中，路由中，总之，。l表示链路权值。

这里基于改进的算法对图7进行评估。

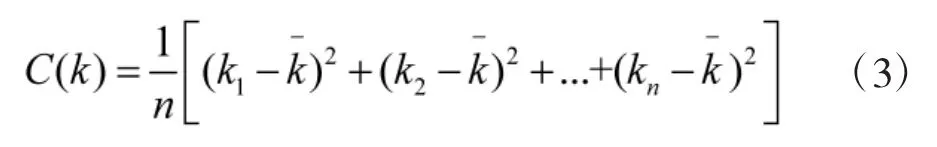
同样可将公式简化为：

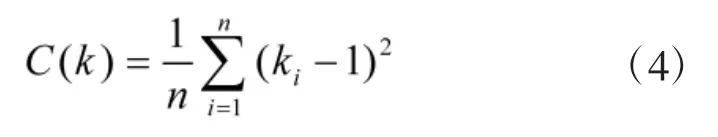
下面应用新的算法对图7中链路及节点的权值进行计算，经计算链路权值，，相对应的节点权值，那么则，因此，带入式（4）可得网络波动性度量值 C（k）=4.91。

2.2 新算法与传统算法仿真结果对比

将新算法应用于图1～图6波动性评估，与传统算法的评估结果进行对比，结果如表2、表3所示。

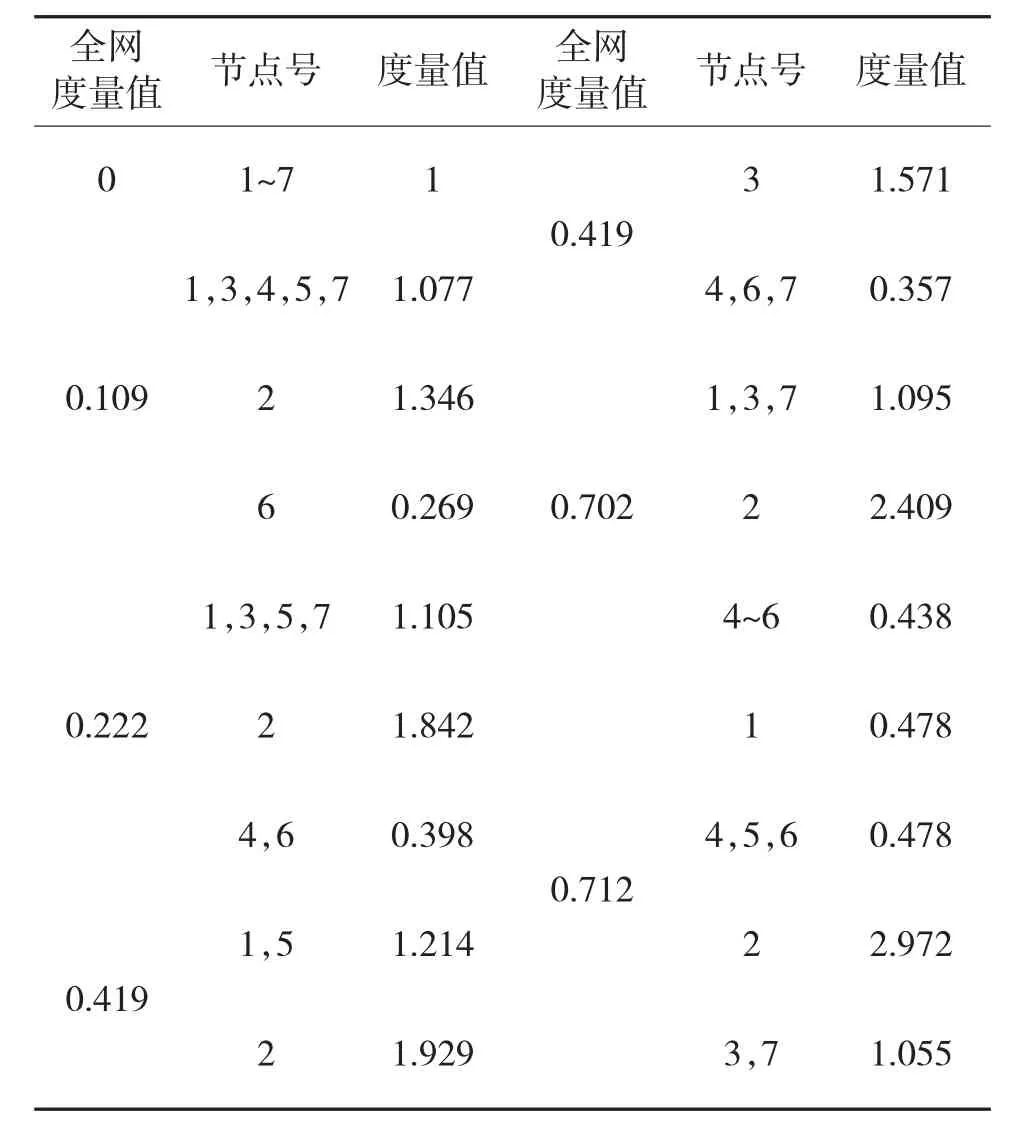
表2 新算法得到图1～图6的网络波动性度量值

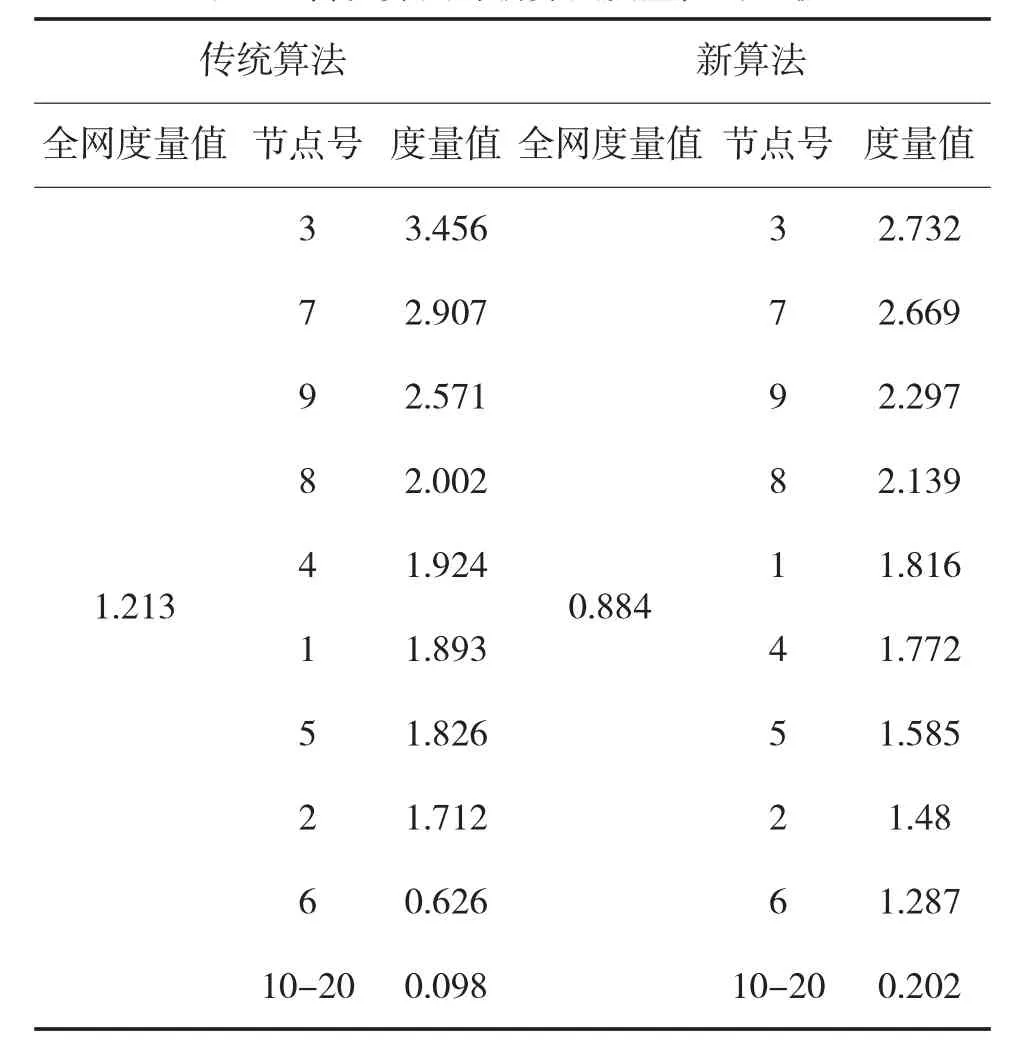
表3 传统算法与新算法度量值的比较

通过对比传统算法评估结果（表1）与新算法结果（表3）可知，对于简单网络，两种算法均能正确表示节点的重要程度以及网络的波动大小。但是新的算法得到的不同网络的波动性度量值较小，而且节点间的度量值彼此差距较小，不会出现节点波动性度量值ki=0的情况。因为新的算法路径的权值分配与实际更接近，路径加权的方法使量化程度更为细致。总之，对于简单网络拓扑结构波动性的评估，新算法优越性不明显，下面将新算法推广到复杂网络评估，验证其是否具有明显的优越性。

3 将新算法应用于复杂网络评估——布尔行列法的引入

对于简单的拓扑结构图，可以通过观察清晰地得到所有的节点间通信的路由，经过简单的统计后便可利用上述公式进行波动性评估。但军事通信网往往节点众多，节点间路由复杂，仅旅级的骨干网就有几十个节点，抽象为拓扑图后，光靠观察很难准确找到任意两节点通信的全部路由，因此，在下文中引入了布尔行列法进行路径的寻找。

3.1 布尔行列法介绍

在阅读的文献中，布尔行列法主要用于简单网络的路由探寻，对于复杂网络，由于高阶行列式计算难度大很少有学者采用。随着MATLAB广泛用于矩阵的计算处理，高阶行列式的计算以及布尔行列法的推广有了很大的便利。

布尔行列法的基本思想是对于给定一个网络的关联矩阵H，矩阵反应节点间连通路由中的链路（没有链路用0表示），将一个同维数的单位矩阵E与该关联矩阵相加，得到E+H矩阵。将矩阵E+H中对应源节点的列以及对应汇节点的行元素删去，构成一个行列式|S|，将|S|展开为布尔积的和，则可以得到源节点到汇节点的路集[7]。

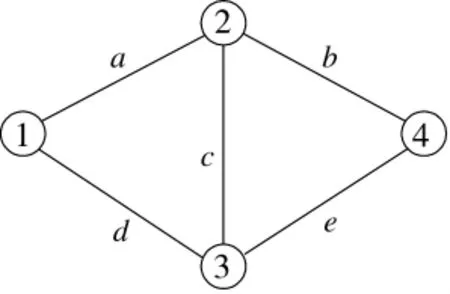
图8 布尔行列法示例图

3.2 布尔行列法应用于复杂网络路由探寻

随着军事通信技术的发展，战术互联网逐渐成为战场通信的骨干力量。美、英、法、加拿大、澳大利亚等北约组织国家早在20世纪60年代后期就开始研制战术互联网[8]，近年来对此的研究更加深入。

战术互联网的主要功能是为旅和旅以下部队提供无缝隙通信网络平台[9]。因此，旅级战术互联网是覆盖面积较大，较为复杂的战场通信网络。相对于只有几个节点构成的简单网络，旅级战术互联网通常由十几个甚至几十个节点构成。接下来将借助MATLAB将布尔行列法推广到较复杂的某旅级战术互联网的路径探寻。

图9 某旅级战术互联网拓扑结构图

图9为某旅级战术互联网拓扑结构图，骨干网和子网总共含有20个节点。所以布尔行列法E+H为20*20矩阵，任意两节点通信时（根据源节点和汇节点的编号删除对应E+H中的行和列），由MATLAB可以方便求出对应矩阵的行列式|S|，从而得到所有的路由。

假设节点1与节点6进行通信，MATLAB模拟过程如下：

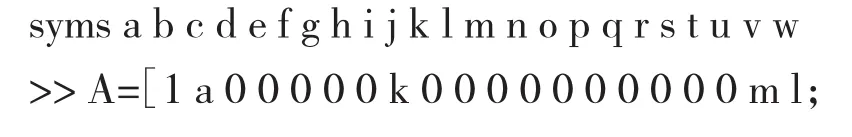
对行列式计算结果进行删选统计，得到符合条件的运算结果为：

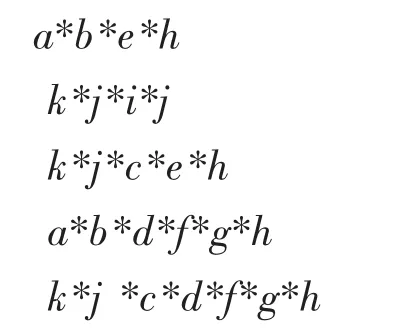
即节点1与节点6之间存在路由abcih，路由abeh，路由 kjih，路由 kjceh，路由 abdfgh和路由 kj cdfgh共6条，MATLAB计算结果与实际完全相符。如果仅通过观察，很难准确找到所有路由。如果没有计算机仿真，复杂网络路径探寻将是一个很大的工作量，这也是布尔行列法通常只用于简单网络路径探寻的原因。仿真结果充分证明：布尔行列法不仅可以应用于简单网络的路由探寻，对于复杂网络，此算法也可以准确有效地探寻出所有路由，布尔行列法完全可以推广到复杂网络的路由探寻。

3.3 新算法与传统算法仿真结果对比

基于布尔行列法MATLAB可以方便的探寻出图9任意两节点间的所有路由，每次两节点间的通信对经过的链路进行权值标注，所有节点两两通信结束后将每条链路的权值进行求和统计，进而求出各个节点的权值，带入式（3）可以求得节点和网络的波动性度量值。

下面分别利用传统算法与新算法对图9美陆军旅级战术互联网拓扑结构进行了波动性评估，两种算法的评估结果如表3所示。

由表3可以看出针对复杂网络，新算法与传统算法相比，新算法依然具备节点间的度量值彼此差距较小评估更细致的优点，除此之外，节点间的度量值大小次序也有不同。传统算法中，节点4的度量值为1.924大于节点1（度量值1.893），而在新算法中，节点 4（度量值 1.772）小于节点 1（1.816），这会引起对哪个评估算法更为准确的思考。

下面针对节点1和节点4的波动性度量值比较问题进行理论验证并仿真。节点波动性度量值的大小反应的是节点在网络中的重要程度，即对全网络波动性的影响程度。采用分别将节点1节点4删去，对得到的新网络分别用传统算法和新算法进行全网波动性评估得到波动性度量值，再与原网络波动性度量值进行比较，判定去掉哪个节点对全网波动性影响更大。计算结果如表4、表5所示。

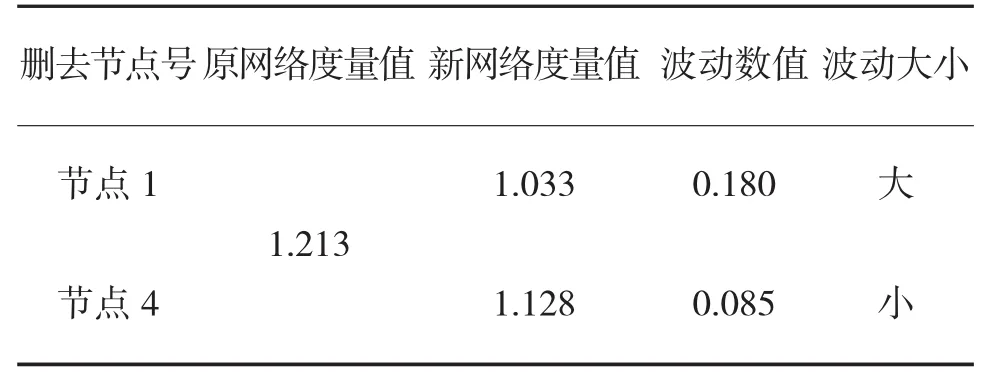
表4 传统算法对节点1节点4重要性比较

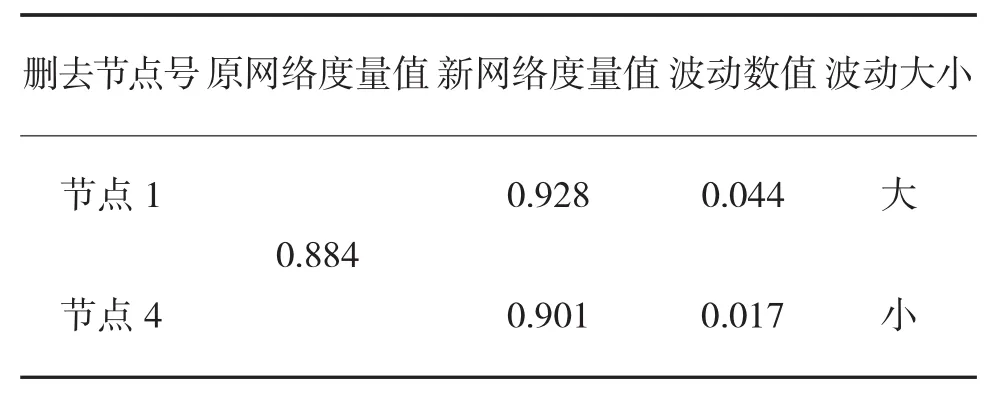
表5 新算法对节点1节点4重要性比较

通过计算结果可以看到，无论传统算法还是新算法都显示：删除节点1比删除节点4对网络波动性度量值影响程度大。这说明节点1的重要程度更高，波动性度量值应高于节点4，所以，在复杂的网络评估中，传统算法因其与实际相符程度低，算法粗糙具有局限性，不能非常准确地评估节点和网络的波动性。相对于传统算法，新的算法更加贴合实际，算法准确评估细致，能够准确反映节点及网络的波动情况。

4 结论

本文首先介绍了传统的网络波动性评估算法，并对传统算法进行了改进，提出了更贴合实际的基于路径加权的复杂军事通信网拓扑层波动性评估算法。同时，将通常用于简单网络路由探寻的布尔行列法推广到复杂网络，借助MATLAB仿真，证明布尔行列法用于复杂网络路由探寻的可行性。最后将新算法推广到复杂网络波动性的评估，对新算法与传统算法的评估结果进行比较分析，研究结果表明：传统算法不能准确评估复杂网络波动性，而新算法具有较好的区分度和准确度，可将其用于复杂网络拓扑层波动性的评估。