掩护突防中雷达干扰无人机最优配置方法*

林晓烘，张春雷，王琳琦，叶灵军，甘厚吉

（海军工程大学电子工程学院，武汉 430033）

0 引言

随着雷达组网技术的快速发展[1]，远距离支援干扰对突防战机编队的掩护作用逐渐减弱，随队支援干扰对飞机的飞行性能要求较高，且面临生存威胁[2]。雷达干扰机由于其成本低、对干扰设备要求低、生存能力强等优点[3]，可以飞临敌方上空实施近距离干扰，实现对敌方雷达网的有效压制，成功掩护己方空中编队突防。因此，雷达干扰无人机实现抵近干扰将成为未来空中突防作战的一个重要手段。

目前，针对雷达干扰无人机在掩护突防中干扰策略的研究受到了越来越多的重视。李昌锦等提出了基于融合中心检测概率加权积分的组网雷达干扰资源优化分配方法[4]；蔡小勇等建立了干扰条件下雷达探测威力模型，对分布式干扰系统的掩护区域进行了分析[5]；吴志峰等研究了无人机实施电子干扰时的路径规划问题[6]；党双平等通过计算静态和动态压制扇面来衡量雷达干扰无人机的动态效能[7]；尹成义等从电子干扰的压制边界入手，提出了一种针对敌方舰艇编队实施干扰的舰载无人机空间配置方法[8]。上述文献针对无人机干扰功率分配或空间配置进行了讨论，为雷达干扰无人机掩护突防作战的研究奠定了基础。然而，无人机的干扰功率分配和空间配置密不可分，不同的干扰功率分配方案下无人机的空间配置也将不同。鉴于此，本文在分析干扰条件下雷达网探测概率模型的基础上，综合考虑无人机干扰波束指向和空间配置对雷达网探测概率的影响，提出了一种无人机掩护突防的最优干扰策略实现方法。

1 无人机噪声干扰条件下雷达网的探测概率

为保证我方空中编队打击的突然性，雷达干扰无人机须先期接近敌方雷达阵地并对其雷达施放有源干扰，使敌方雷达对我空中编队的探测概率大大降低，有效掩护我方编队的突防。在突防过程中，雷达、干扰无人机和突防编队之间的相对几何关系如图1所示。

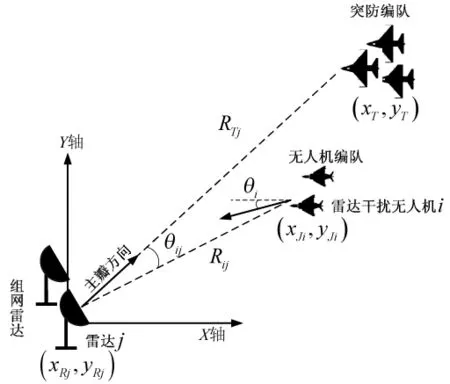
图1 雷达干扰无人机掩护空中突防的几何关系图

当第j部雷达天线主瓣对准我方编队时，第i架无人机相对于该主瓣方向的夹角为θij，此时，第j部雷达接收到的编队回波功率为：

式中，Ptj、Gtj分别为敌方第j部雷达发射功率和天线主瓣增益，j为第j部雷达发射载波波长，σ为我方突防编队的雷达散射面积。

第j部雷达接收到干扰信号功率为：

式中，Pwi为第i架无人机干扰发射功率，N为无人干扰机架数，θi为其干扰波束主瓣相对于X轴的夹角，φij为第j部雷达与第i架无人机之间的视线与X轴的夹角，可通过下式求解：

Gi（θ）为与第i架无人机干扰天线波束主瓣中心偏离θ角方向上的增益，可用下式近似表示：

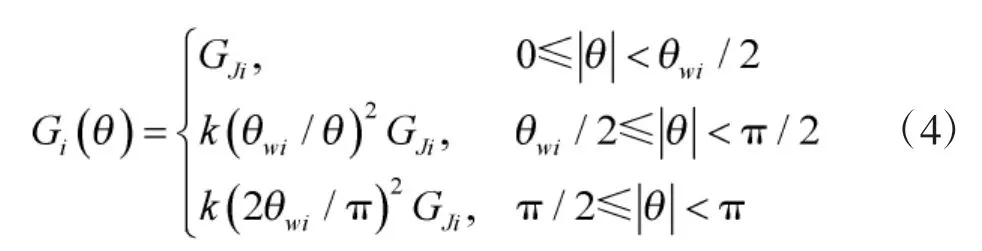
式（4）中，θwi表示第i架无人机干扰天线主瓣3 dB波束宽度，GJi为其主瓣增益；当干扰机采用高增益锐方向天线时，k取[0.07，0.1]，当采用宽波束低增益天线时，k取[0.04，0.07]；式（2）中，G（θij）为第j部雷达在第i架无人机方向上的增益，其增益值可用类似式（4）计算，此时式（4）中干扰天线主瓣3 dB波束宽度、干扰天线主瓣增益依次替换为雷达天线的3 dB波束宽度和主瓣增益。

式中，Pdj、Pfa，j分别表示干扰条件下第 j部雷达的探测概率和虚警概率。

假设敌方防空阵地雷达工作在组网方式，且采用秩K融合法计算其综合探测概率，那么组网雷达对目标综合的探测概率可通过下式求解：

式中，si表示第i种组合下未探测到目标的M-n部雷达的集合，Pdsi表示在该集合中各雷达的探测概率，表示第i种组合下探测到目标的n部雷达的集合，为在该集合中各雷达的探测概率。

此外，雷达对第i部无人机的探测概率Pzwi也可通过上述步骤进行求解，此处不再赘述。

2 无人机空间配置与功率分配优化模型

当敌方各防空雷达和我方突防编队掩护位置确定之后，组网雷达对我方突防编队的探测概率将是各无人机的位置和波束指向θi的函数，此时式 （6） 中的 Pdi和 Pz可分别重新记为和，其中。则我方无人机编队可选取合适的位置布设和干扰天线波束指向，使得敌方雷达组网综合探测概率在我方编队突防点处的探测概率达到最低，此时对应的无人机位置即为最优的配置位置，其波束指向决定了最佳的功率分配方案。

此外，各无人机的自身安全也需考虑，也就是说，无人机所处位置必须使得敌方组网雷达对无人机的探测概率须足够小（本文取典型值0.1）。由此，当我方突防编队突防点确定之后，无人机的最优空间配置和波束指向可通过下式求解：

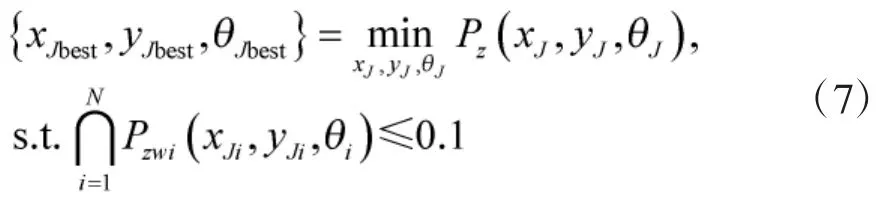
3 利用粒子群算法求解优化模型

相比遗传算法等其他智能优化算法，粒子群算法（Particle Swarm optimization，PSO）具有规则简单、全局搜索能力强、收敛速度快等优点[10]，已广泛应用于函数优化、神经网络训练、模糊系统控制等应用领域。PSO算法通过迭代搜索来模拟鸟类觅食过程中的协作和竞争，最终获得复杂问题的最优解。

式中，w是惯性权重系数，c1和c2称为加速度因子，r1和 r2为[0，1]之间的随机数。

由式（7）可见，PSO算法需要在3N维空间搜索最优值，每个粒子的适应度函数由组网雷达探测概率决定，历次搜索中，粒子群的个体极值和全局极值根据搜索过程中出现的探测概率极小值来确定，整个求解的过程见图2所示。

4 仿真与分析

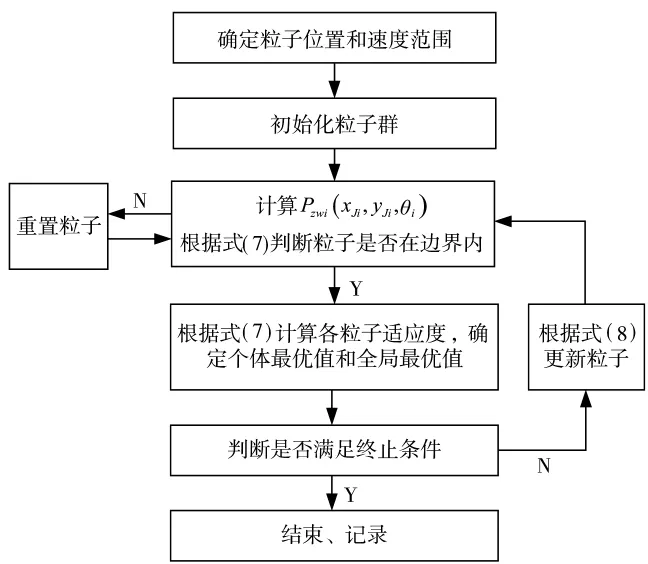
图2 本文算法流程图

无人机工作参数设置为：无人机干扰发射功率Pwi=15 W，主瓣增益GJi=2 dB，主瓣波束宽度θwi=20°，无人机雷达散射截面积σw=2 m2，干扰天线波束方向性常数k=0.04，我方突防编队雷达散射截面积σT=80 m2。如图1所示，以敌防空警戒雷达阵地中心处为原点，建立坐标系，其组网雷达探测概率采用秩1融合法计算。突防编队沿X轴负方向进行突防，要求当我方编队从敌雷达最大探测距离处突防至敌警戒雷达阵地中心50 km处时，无人干扰机都要对敌方雷达网进行有效压制。干扰无人机编队在编队突防前，应先到达部署区域待命，一旦编队突防至敌警戒雷达最大探测距离处，即可实施干扰。

粒子群体规模为50，迭代次数为4 000，惯性权重系数为0.85，加速度因子为2。

本文仿真试验根据以下3种情况，分别求解当我编队突防至距敌阵50 km处，且敌方雷达网对我编队的探测概率最小时，无人机编队应部署的位置和干扰波束的指向。

1）单架无人机干扰单部雷达仿真试验

假设敌方仅有一部防空警戒雷达，其天线发射功率为Pt=800 kW，主瓣增益Gt=40 dB，主瓣波束宽度θr=2°，载频fc=3 GHz，天线波束方向性常数 kr=0.08，虚警概率设置为Pfa=10-6，雷达位于坐标系原点。在此种场景下，为了干扰能量能尽量多地进入雷达接收机，无人机部署应在X轴上，且其干扰波束对准雷达。此时，随着无人机部署位置的变化，雷达对突防编队和无人机的探测概率也随着变化，见图3。

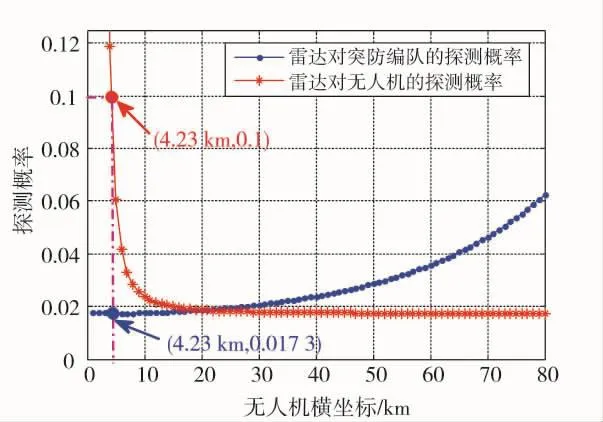
图3 单架无人机干扰单部雷达时的无人机位置与探测概率关系曲线

由图3可见，随着无人机离雷达距离越远，雷达对突防编队的探测概率越高，对无人机的探测概率越低。这是由于随着距离的增大，进入雷达接收机的干扰信号能量越小，导致雷达探测突防编队的信干比增大，从而得到更高的探测概率。另外一方面，雷达对无人机的回波与彼此距离的四次方成反比，而进入雷达接收机的干扰能量与距离的二次方成反比，因此，随着距离的增大，干扰能量的衰减慢于无人机回波的衰减，使得雷达接收无人机的回波信干比下降，雷达对无人机的探测概率越来越小。根据式（7），无人机部署的最近距离是4.23 km，此处对应雷达的探测概率为0.1，该距离也是最佳部署距离，使得雷达对突防编队的探测概率达到最低，为0.017 3。在此场景下，式（7）求解的是二维优化问题，利用PSO算法求得最佳干扰距离是4.230 1 km，对应的探测概率为0.017 31，求解误差很小。

2）单架无人机干扰两部组网雷达仿真试验

假设敌方阵地中有两部相同的组网雷达，其工作参数与上个试验一致，坐标分别位于（0 km，8 km）和（0 km，-8 km）。由于无人机干扰天线指向不能快速切换，并不能将主瓣中心方向都分时对准两部雷达。不同天线指向意味着对雷达网各雷达分配的功率不同。本次试验中干扰波束指向以X轴负向方向为0°，逆时针偏转为正。图4为不同干扰波束指向条件下，雷达网对突防编队的最低探测概率及其对应的无人机部署位置。

图4 一架无人机干扰两部相同雷达时干扰波束指向与无人机最佳部署位置关系曲线

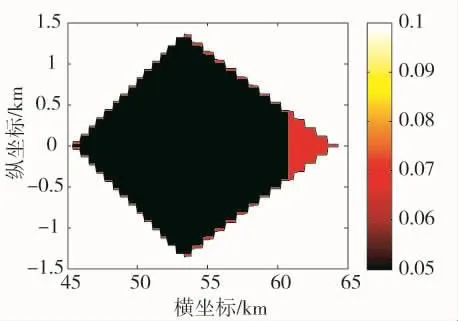
图5 一架无人机干扰两部相同雷达时最佳干扰波束指向下无人机部署位置与雷达探测概率关

由上图可见，最佳的波束指向角为0°，其对应的无人机部署位置为（45.4 km，0 km），这是由于在该处位置是无人机干扰主瓣刚好能够完全覆盖两部雷达且距离雷达最近的距离，也就是说，干扰波束主瓣边沿刚好照射到两部雷达。同样地，其他波束指向下，无人机部署的位置也是确保其干扰主瓣要覆盖两部雷达，其相应的部署位置见图4，可见随着波束指向偏离0°的角度越大，最佳的部署位置也离雷达阵地越远，使得最终雷达对突防编队的探测概率越大。图5为波束指向为0°时，干扰机部署位置跟雷达探测概率之间的关系。通常，在探测概率低于0.1时，认为干扰有效。图5描述了干扰有效情况下无人机可部署的范围，其中深黑色区域对应的雷达探测概率在0.05～0.06之间，是无人机执行干扰任务最佳的区域。

考虑两部雷达的发射增益不同，分别为800 kW和400 kW，其他参数一致。此时，不同干扰波束指向下雷达对突防编队的探测概率及其对应的最佳部署位置坐标如图6所示。由图可见，最佳指向为-1°，对应的无人机部署位置为（45.5 km，-0.8 km）、雷达对突防编队的探测概率为0.051 5。最佳干扰波束指向下，可实现有效干扰的无人机部署位置如图7，可见此时飞行区域成扁长形，无人机宜在深黑色区域展宽对雷达网的干扰。

3）多部无人机干扰多部组网雷达仿真试验

假设敌方防空阵地有雷达4部，其坐标如表1所示，4部雷达工作参数与本节第一个仿真试验参数设置一致，我方雷达干扰无人机2部。此时两架无人机最佳干扰波束指向和部署位置的求解将是6维优化问题，由本文算法求得的最佳干扰波束指向和无人机部署位置见表1所示。

图6 一架无人机干扰两部不同雷达时干扰波束指向与无人机最佳部署位置关系曲线

图7 一架无人机干扰两部不同雷达时最佳干扰波束－指向下无人机部署位置与雷达探测概率关系

表1 敌雷达位置及无人机最佳干扰波束指向、部署位置

表1第1组数据针对雷达网各雷达呈线性密集布置进行仿真。此时，在最佳部署策略下，两部干扰机部署的位置很接近，干扰波束指向一致，在此最佳干扰距离，两个干扰主瓣均刚好完全覆盖4部雷达。

第2组数据针对各雷达网呈分散布置进行仿真。由表1可见，最佳干扰策略下，无人机1干扰波束主瓣覆盖雷达3和雷达4，第一旁瓣覆盖雷达1和雷达2，而无人机2的情况与无人机1相反。对于分散布置的雷达网，虽然把无人机部署得足够时干扰主瓣可以完全覆盖4部雷达，但距离带来的衰减大于主副瓣增益的差别。

第3组数据针对雷达网各雷达呈正方形布置进行仿真。可见，此种情况下，无人机1的干扰主瓣刚好完全覆盖雷达1、雷达2和雷达4，无人机2的干扰主瓣覆盖雷达1、雷达2和雷达3。虽然雷达1和雷达2距离无人机较远，但它们可以同时被两个干扰主瓣照射，而雷达3和雷达4仅有一个干扰主瓣照射，但它们距无人机距离更近，综合而言，干扰功率分配比较均匀。

5 结论

如何选择合适的空间位置和干扰波束指向，使得雷达网探测概率最低是制定掩护突防中雷达干扰无人机干扰策略时要考虑的重要因素。当敌雷达网雷达数量多，无人机架数多时，这将是一个复杂的优化问题。利用粒子群优化算法可以快速求解出特定掩护距离下无人机最佳波束指向和空间位置，进而通过变换掩护距离还可以得到无人机最佳动态干扰策略。