耦合界面力的两相流相场格子Boltzmann模型∗

李洋 苏婷 梁宏 徐江荣

(杭州电子科技大学理学院,杭州 310018)

(2018年6月25日收到;2018年9月14日收到修改稿)

1 引 言

格子Boltzmann(LB)方法[1,2]是近三十年来发展起来的一种流体系统建模和模拟方法.它不再基于宏观连续介质模型的Navier-Stokes方程,而是直接从微观模型出发通过描述流体粒子分布函数的演化再现复杂流动的宏观行为.因此,LB方法相比传统数值方法有一些独特优势,而受到了众多学者的关注,并已广泛应用于多个学科领域,如多孔介质中传热传质、湍流的直接数值模拟、多相流体流动与传热、颗粒流[1,2]等.特别是LB方法的介观属性,可以使其直接描述多相流体系统中流体间与流固间的相互作用,因而可以方便地模拟多相流体流动,这也被认为LB方法区别传统数值方法的最大优势之一.

目前,许多学者已经根据流体间微观相互作用力的不同物理背景,提出了多种不同类别的两相流LB模型[1,2],包括颜色模型、伪势模型、自由能模型、基于相场理论的模型.在这些提出的LB模型中,基于相场理论的两相流LB模型[3−9]因具有坚实界面追踪的物理机制,近年来受到了广泛关注,并且已成功地应用于复杂多相流动问题的研究[10−13].He等[3]基于相场理论提出了第一个不可压两相流LB模型,其基本原理是通过引入序参数分布函数来追踪流体界面,而用另一个压力分布函数来求解流场.然而,Zheng等[4]指出He模型存在所恢复界面追踪方程与相场理论中Cahn-Hilliard方程不一致的问题,并通过在界面演化方程中引入序参数分布函数的差分项,提出了与相场方程相一致的LB模型.另外,针对He模型所模拟大密度比的限制,Lee和Liu[5]提出了二阶混合差分格式来离散流体间的相互作用力,从而提高了模拟大密度多相流动问题的数值稳定性.然而,一些学者指出混合差分格式的使用会导致Lee模型不满足全局质量守恒[14].受Zheng等模型的启发,Zu和He[6]在界面演化方程中引入一种平衡态分布函数的空间差分项,从而也能够准确恢复到Cahn-Hilliard方程.另外,为了恢复正确的不可压Navier-Stokes方程,Zu和He在流场的LB算法中引进一些复杂的源项,这导致模型中速度和压力满足一组隐式方程,需要通过预估与校正方法来求解.最近,Liang等[7]也从相场理论出发构造了一类界面求解精度更高且数值稳定性更好的两相流LB模型,并且流场中宏观速度和压力的计算更为简便.

综上所述,两相流的相场LB模型得到了较大的发展.然而,在相场LB模型中,存在着一类特殊的界面力[15].通过Chapman-Enskog理论分析发现,相场LB模型中均存在着界面力的尺度与理论分析结果不一致的问题.另外,为了描述流场的信息,相场LB模型中均含有一些复杂的外力项.针对这些问题,本文考虑了界面力的尺度效应,并提出了更加简单的外力项分布函数.通过多尺度分析,本模型也能恢复到正确的宏观控制方程.

2 控制方程和数学模型

2.1 控制方程

在相场理论中,用于描述多相系统中相界面运动的宏观控制方程是著名的Cahn-Hilliard(CH)对流扩散方程[6,7],

这里,ϕ是标识不同流体的序参数,u是流体速度,M是迁移率,µ是自由能的化学势,在相场理论中可以表示为

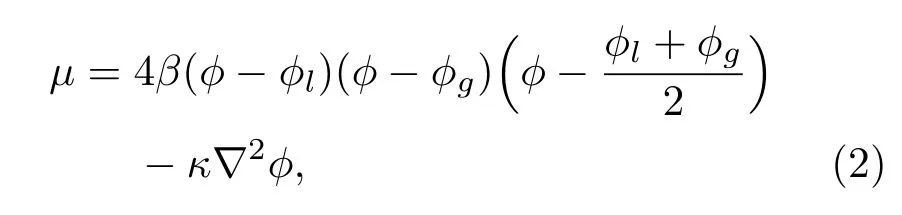
其中ϕl和ϕg分别表示液相和气相的序参数,而相界面可以表征为ϕ=(ϕl+ϕg)/2的等值线,参数β和κ由界面厚度D和表面张力σ决定,

另外,为了描述多相流体流动,界面追踪CH方程需要耦合流体动力学方程.根据文献[7],含有外力项的不可压缩黏性流体的Navier-Stokes(NS)方程可表述为:

其中,ρ是流体密度,p是压力,ν是流体黏性系数,F为总外力,包含外力项G和表面张力Fs,在本文的数值模拟中,我们取常用的势形式Fs=−ϕ∇µ或Fs=µ∇ϕ[6,7,15]来减少流体界面处的虚假速度.

2.2 两相流格子Boltzmann模型

为了求解CH方程和NS方程,本文引入了两个独立的分布函数fi和gi,其对应单松弛LB模型的演化方程可分别表示为:

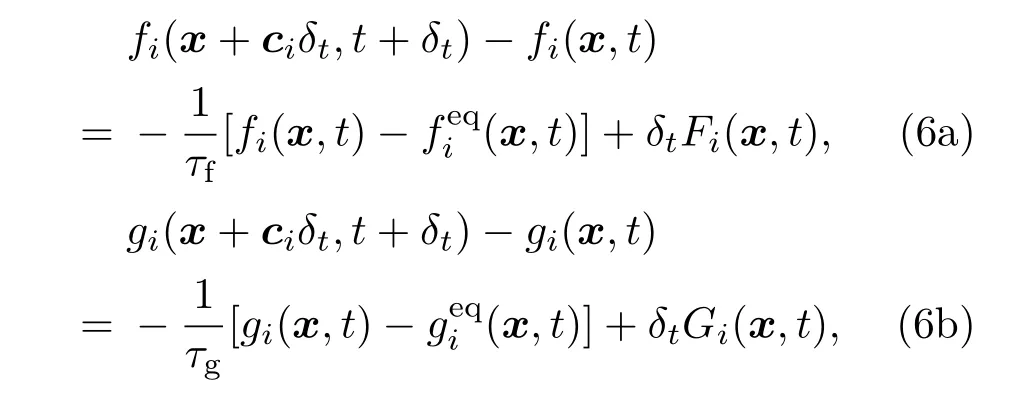
其中τf和τg是分别与迁移率M和运动学黏性系数ν有关的松弛因子,fi(x,t)是粒子在t时刻x位置的序参数分布函数,gi(x,t)是密度分布函数,相应的平衡态分布函数和分别被定义为[7]:

这里

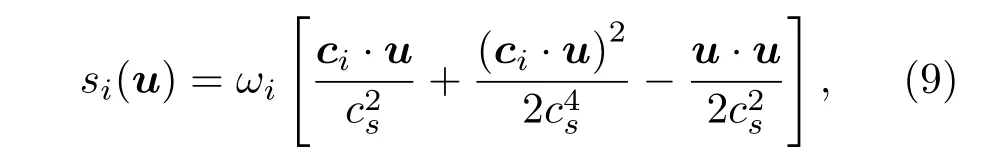
其中η是调节迁移率大小的参数,ωi是权系数,cs为格子声速.格子速度的离散模型决定着η和ωi的取值,对于D2Q9模型,相应的权系数√ω0=4/9,ω1−4=1/9, ω5−8=1/36,cs=离散速度ci为

其中,c= δx/δt,δx是单位格子大小,δt为时间步长.本文中,我们取c=δx=δt=1.

为了准确恢复到CH方程,Liang等[7]在演化方程引入了可以局部计算的时间导数项,其对应的源项分布函数可定义为

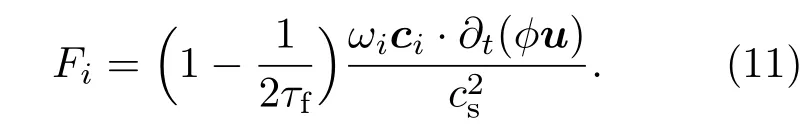
在不同的两相流相场LB模型中,外力项分布函数具有不同的形式[6,7,15].在原始的相场LB模型中,外力项分布函数可定义为[7]

基于Chapman-Enskog多尺度分析,我们发现速度的计算表达式中外力应为o(ε)尺度,然而Fa为o(ε2)尺度,这就导致速度计算式出现了尺度不一致的问题.界面力尺度与理论分析不一致问题同样存在于其他的相场LB模型[6,15]中.另外,我们注意到为了恢复正确的不可压Navier-Stokes方程,相场LB模型在流场的演化方程中均引入了较为复杂的外力项分布函数,这影响了模型的实现难度和计算效率.针对上述问题,我们考虑了尺度效应,并提出了一种新的更加简单的外力项分布函数

本模型中序参数ϕ的计算如下:

宏观量密度ρ可以看作序参数ϕ的线性函数,

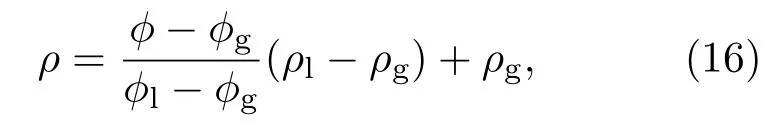
其中ρl与ρg分布代表液相和气相的密度.修正后的速度表达式及压力计算式可表示为:

通过Chapman-Enskog多尺度分析[7],可以证明本模型中界面追踪的LB演化方程(6a)可正确地恢复到Cahn-Hilliard控制方程,并且迁移率M与松弛因子关系可表示为

接下来,我们简要地论述本文提出新的外力项分布函数的LB演化方程(6b)如何恢复到不可压流体的Navier-Stokes方程.根据外力项分布函数的表达式(14),其对应的矩条件为

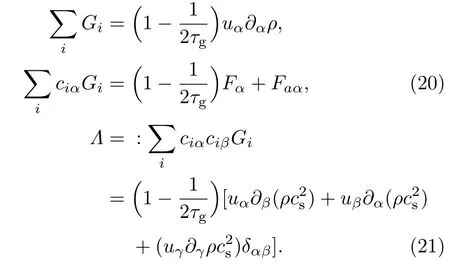
为了恢复正确的宏观控制方程,我们引入如下的多尺度展开式:

其中ϵ是非常小的展开参数.将LB演化方程(6b)Taylor展开到δ2t量级,并应用上述的多尺度展开式可得

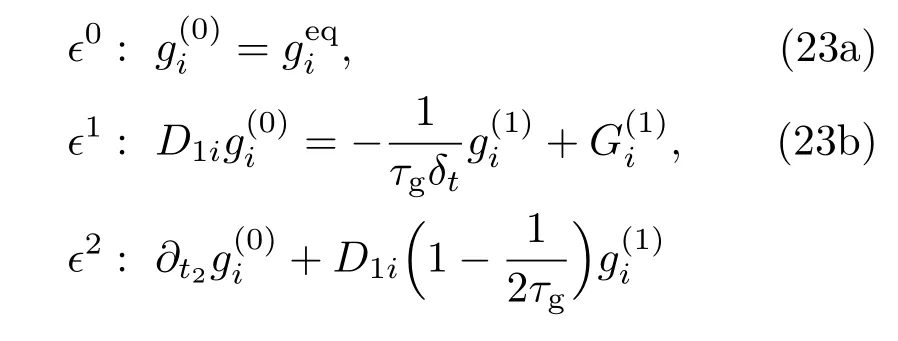
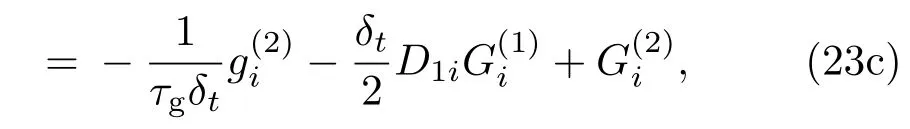
其中,D1i= ∂t1+ciα∂1α. 由分布函数和Gi的矩条件,gi的零阶矩可定义为[10]

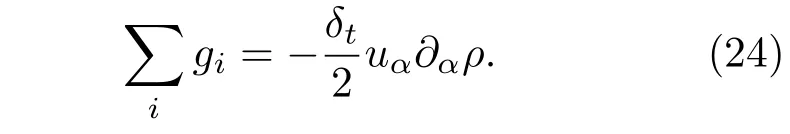
进一步,应用多尺度展开式到(17)和(24)式,可得分布函数gi满足如下性质

利用上述结果,对(23b)式分别求零阶和一阶速度矩,可以得到t1尺度上的宏观方程

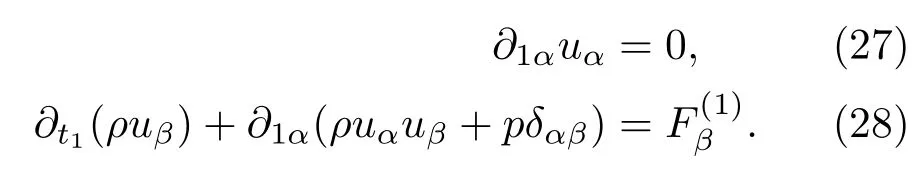
同理,t2尺度上的宏观方程可从(23c)式的零阶和一阶速度矩得到,

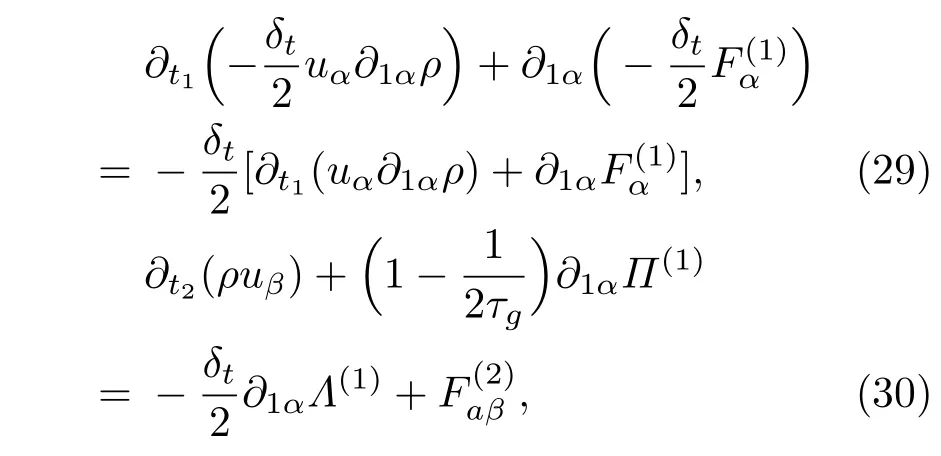
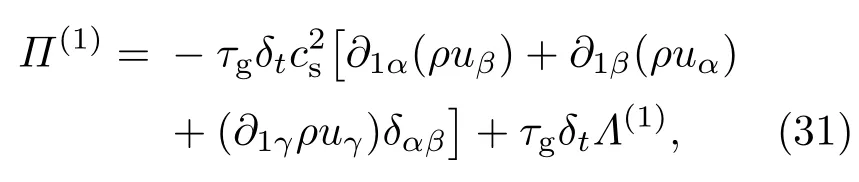
其中,阶数为O(δtMa2)的一些项已被略去.代入上述结果可将(30)式改写为

对t1和t2尺度上的方程进行尺度黏合,最终发现可以正确地恢复到不可压缩黏性流体的Navier-Stokes方程组(5a)和(5b),并且运动学黏性系数ν(23b)式和各阶矩条件,经系列计算最终可得到为

在古诗文的词汇中，实词的意义相对固定，随着时代的更迭，会产生相应的拓展和引申，但总的来说学生易于掌握，难的莫过于虚词。刘彦和将常见的虚词作了如下归类：“至于夫惟盖故者，发端之首唱；之而于以者，乃扎句之旧体；乎哉矣也，亦送末之常科。”并指明虚词在作者回环婉转的巧妙运用下，文辞就会变得严密。因此，作者在创作过程中会努力避免虚词的运用出现谬误，那么我们在阅读过程中同样要将虚词理解准确。否则，即使理解了文意也是不严密的。当然，在教学实践中不能完全按刘彦和的方法来辨析，毕竟《文心雕龙》成书于南朝，此后的词汇在词性和词义上都产生了变化与演进。

在数值模拟中,需要对时间导数项和空间导数项进行离散计算.本文中选用显式的欧拉差分格式来计算时间导数项,

针对空间导数项,为了保证多相系统的全局质量守恒,我们采用如下的各向同性的二阶中心差分格式[14],

其中χ表示任意变量.

3 数值结果和讨论

在本节中,首先通过模拟几个典型的两相流问题,包括静态液滴、液滴合并、亚稳态分解和单模瑞利-泰勒不稳定性问题,来验证所提出的两相流相场LB模型的准确性和稳定性.接着,利用本模型来研究随机扰动分布的多模瑞利-泰勒不稳定性问题,着重考察雷诺数对相界面的影响规律.

3.1 静态液滴

首先模拟静态液滴这一基本的两相流问题用于验证本模型,并由此测量本模型产生的虚假速度.该问题的初始条件设置如下:半径R=25的圆形液滴坐落在100×100的计算区域内,边界四周采用周期性边界条件,其他的相关物理参数设置为ρl=100,ρg=1,ϕl= −ϕg=1,D=5,σ =0.001,τf=0.8,M=0.1,ν=0.1.序参数的初始分布给定为

在这里(xc,yc)=(50,50)是液滴中心的坐标.根据方程(16),可以得到相应的初始密度分布.图1(a)给出平衡状态下整个计算区域的速度分布,以及黑色的实线表示液滴的初始形状,红色的虚线表示平衡状态下的液滴形状.从图中可以发现它们吻合得很好,这验证了本模型能够准确的求解相界面.此外,图1(b)给出了沿着线x=Ny/2的密度分布,可以发现密度场的解析解与通过相场LB方法模拟获取的数值结果相一致.相界面处存在虚假速度一直是数值方法普遍存在的非物理现象.我们进一步统计了本模型产生的虚假速度,结果表明其虚假速度的最大值约为3.57×10−9.在前人的相场LB模型中,Zu和He[6]的模型产生的虚假速度为10−8量级,而Liang等[7]提出的模型在单松弛情况下产生的虚假速度为7.8×10−6.对比前人相场LB模型,可以发现本文修正的LB模型可以获得相对较小的虚假速度.

图1 静态液滴测试 (a)平衡状态下的整个区域的速度分布图,实线和虚线分别代表液滴的初始形状和在平衡状态下的形状;(b)沿着x=Ny/2的密度分布的LB模拟结果和解析解Fig.1.Static droplet test:(a)The velocity distribution of the whole domain at the equilibrium state and the solid and dashed lines respectively represent the initial shape of the droplet and its equilibrium shape;(b)density profile across the interface obtained from LB simulation and corresponding analytical solution along x=Ny/2.

3.2 液滴合并

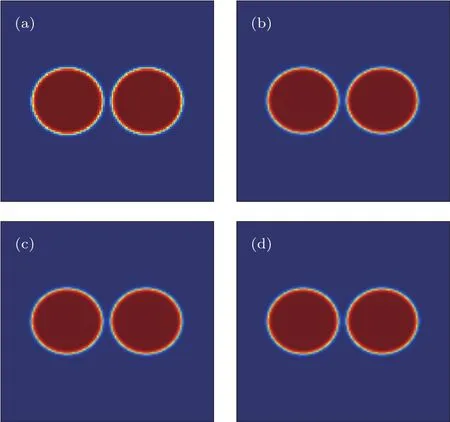
图2 两个液滴的合并过程(d=5,D=2.4) (a)t=0;(b)t=20000;(c)t=40000;(d)t=60000Fig.2.The combination of two static droplets(d=5,D=2.4):(a)t=0;(b)t=20000;(c)t=40000;(d)t=60000.

图3 两个液滴的合并过程(d=5,D=2.6) (a)t=0;(b)t=20000;(c)t=23000;(d)t=50000Fig.3.The combination of two static droplets(d=5,D=2.6):(a)t=0;(b)t=20000;(c)t=23000;(d)t=50000.

3.3 亚稳态分解

进一步,我们模拟了更为复杂的相分离问题[6,17]来验证本文提出的两相流相场LB模型.亚稳态分解,也称相或组分分离现象,是混合流体的一种基本特征.对处于亚稳态状态的均匀混合流体施加一个很小的扰动,此时流体系统是不稳定的,相分离现象将会发生.在我们的模拟过程中,计算区域设置为NX×NY=100×100,四周采用周期性边界条件.初始的序参数分布设定为

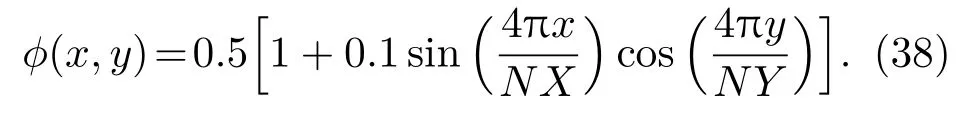
根据密度与序参数之间的线性关系,可以得到相应的初始密度分布.模拟中其他的物理参数设置为:液相密度ρl=10,气相密度ρg=1,ϕl=1,ϕg=0,τf= τg=1,界面厚度D=4,迁移率M=0.5.图4展示了表面张力σ=0.001时两相分离现象的演化过程,从图中可以观察到,两种流体初始时刻处于混合状态,随着演化时间的增加,流体在流体间的相互作用力下渐渐地聚集,从而系统中形成了小液滴且尺寸随时间不断地增大,最终在t=160000时亚稳态分解形成两相流体,上述相分离过程与文献结果[17]定性地相一致.另外,我们进一步研究了表面张力对相分离过程的影响,将表面张力调整到σ=0.01.图5展示了表面张力σ=0.01时两相分离现象的演化过程.从图中可以发现,增大表面张力不会影响相界面的演化图案,但可以加速相分离过程,相比σ=0.001情形可以更快的达到相分离的稳定状态.

3.4 瑞利-泰勒不稳定性

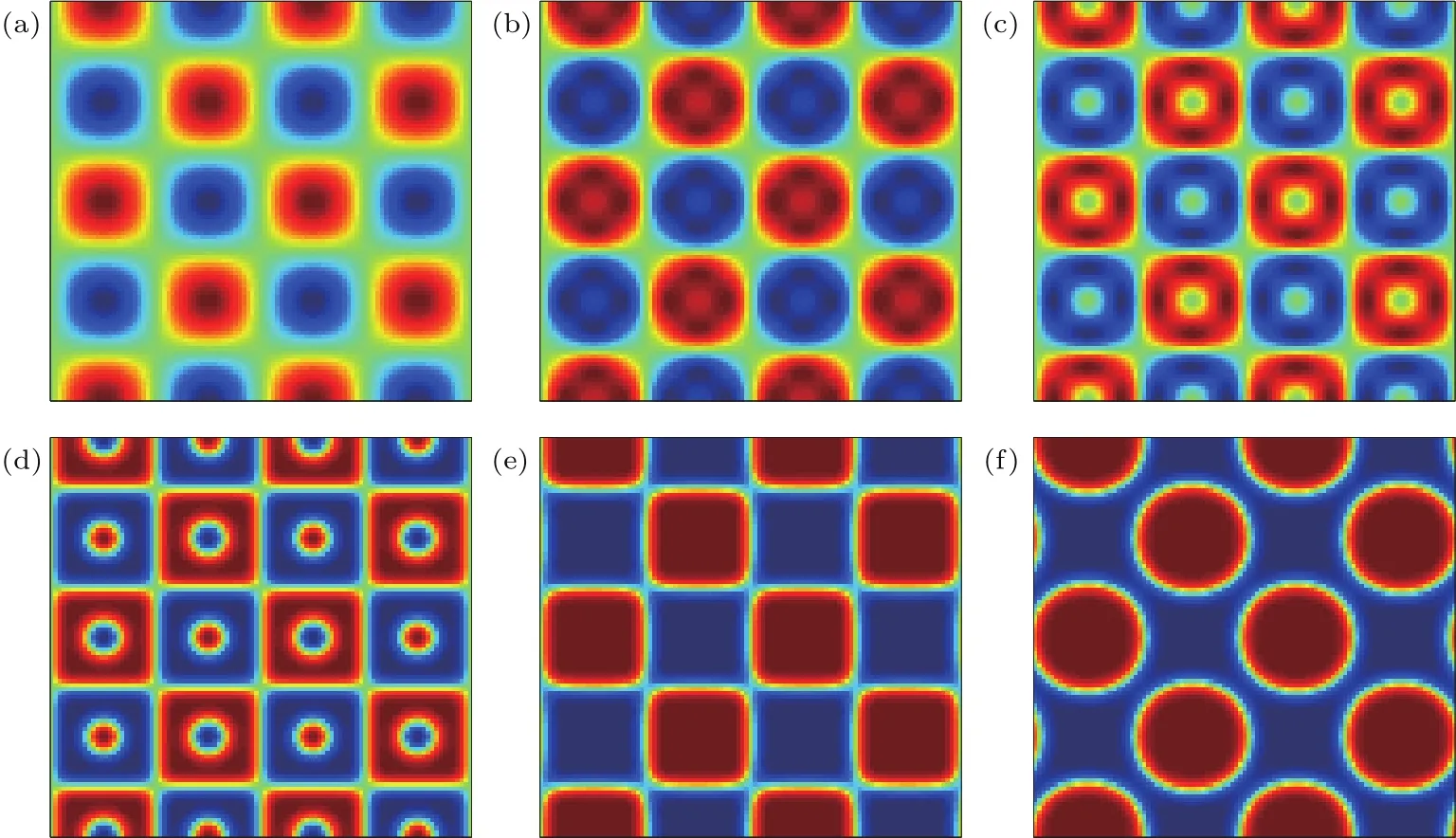
图4 σ=0.001时相分离的时间演化过程 (a)t=0;(b)t=28000;(c)t=38000;(d)t=49000;(e)t=113000;(f)t=160000Fig.4.Time evolution during the phase separating process at σ=0.001:(a)t=0;(b)t=28000;(c)t=38000;(d)t=49000;(e)t=113000;(f)t=160000.

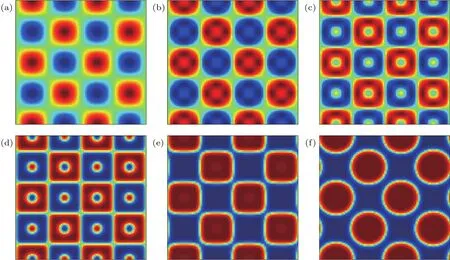
图5 σ=0.01时相分离的时间演化过程 (a)t=0;(b)t=3000;(c)t=4000;(d)t=7000;(e)t=11000;(f)t=16000Fig.5.Time evolution during the phase separating process at σ=0.01:(a)t=0;(b)t=3000;(c)t=4000;(d)t=7000;(e)t=11000;(f)t=16000.

在本小节,我们模拟了两相流体间的经典界面不稳定性现象,即瑞利-泰勒(Rayleigh-Taylor,RT)不稳定性问题[18,19].当密度较大的流体放置于密度较小的流体上层时,给流体界面处施加一个微小扰动,在重力的作用下,上层流体流入下层,下层流体从两侧向上涌入,最终达到混沌混合状态,这种现象称之为RT不稳定现象.最早对RT不稳定性问题的研究可追溯到著名学者Rayleigh[18]对云层形成的研究,后来学者Taylor[19]又在原子核聚变中发现了RT不稳定性现象.自此以后,许多学者对RT不稳定性问题开展了理论、实验或者数值研究,有兴趣的读者可以参考最近关于RT不稳定性的文献综述[20].

我们考虑一个矩形微管道,其高度L和宽度W的比例为4,对两相界面处施加一个微小扰动,其扰动函数给定为

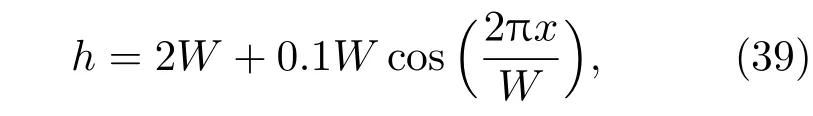
初始的序参数分布则设定为

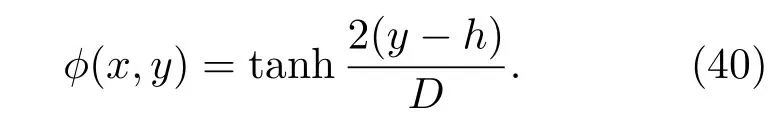
雷诺数(Re)和Atoods数(At)是影响RT不稳定性的两个重要无量纲参数,分别定义为

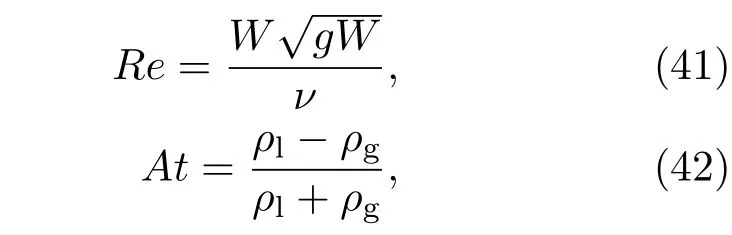
其中,g是重力加速度,为了耦合重力效应,在模拟中对计算区域的所有流体点施加一个重力,其定义为

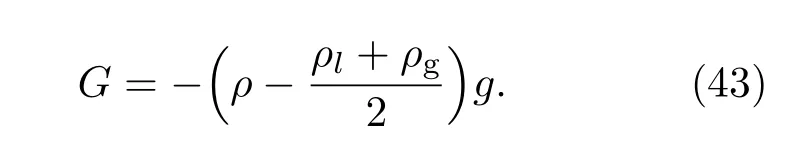
在数值模拟中,液相密度ρl=3,气相密度ρg=1,相应的At数为0.5,其他物理参数设置为:ϕl= −ϕg=1,W=128,=0.04,D=4,τf=0.8,表面张力σ=0.0001.佩克莱数(Pe)的定义如同于参考文献[6,7],并取为50.另外,我们讨论雷诺数对相界面的影响,并通过改变雷诺数的大小可以确定流体黏性系数,进而确定松弛因子τg的值.上下壁面均采用无滑移的边界条件,左右边界应用周期边界条件.图6给出了Re=256时非混相RT不稳定性中相界面随时间的演化图.从图中可以看到,在初始时刻,由于两相界面处受到微小扰动的作用,液相重流体在中间的凹界面处往下运动,而气相轻流体沿着两侧的壁面向上升起,从而分别形成了尖钉和气泡.随着演化的不断进行,尖钉和气泡继续相互渗透,伴随着尖钉两侧向上卷起形成了一对旋转方向相反的漩涡.此后,在流体间的剪切力下,漩涡不断地发展,其尺寸不断地增大.可以发现,各个时刻相界面的演化过程与He等[3]的结果在定性上相一致.我们进一步地考察了Re数对RT不稳定性演化特性的影响,并且模拟了Re=1024较大的情形.图7给出了Re=1024时非混相RT不稳定性中相界面演化图.从图中可以发现,在演化前期,不稳定性的界面演化图案与Re=256情形相类似:液相流体与气相流体相互渗透形成尖钉和气泡,随着时间演化,尖钉向上卷起形成两个关于中间轴对称的漩涡.接下来,相界面呈现出与低Re数情形显著不同的形态.一对漩涡继续发展,其尺寸不断地增大,伴随着在漩涡尾端形成二级漩涡,这一现象并未在低Re数的情形中观察到.随后,流体间界面不稳定性继续发展,在高流体间剪切力作用下,形成了多对漩涡的复杂界面结构.当Re较大时,系统中相界面的非线性程度和流场较为剧烈,此时界面力效应比较显著.因此,我们通过对比本模型和Li等[15]的模型所模拟Re=1024条件下RT不稳定性的结果,来体现界面力的效应.为了消除界面追踪LB模型所带来的影响,本文采用的界面追踪LB演化方程(6a)应用于Li等的模型中.图8给出了Li等的模型计算获取的非混相RT不稳定性中相界面随时间的演化.对比图7的结果,可以发现两种LB模型获得的相界面图案在不稳定性前期差别不大,这是由于在演化前期,不稳定性处于线性增长阶段,流场较为温和,界面力的效应不显著.而在演化后期,不稳定性进入非线性增长阶段,界面力的效应开始显著.从图8可以看出,相界面相比图7变得光滑,在尖钉的尾端未观察到显著的二级漩涡.进一步,我们也定量地统计了不同Re数下随时间演化的尖钉和气泡在y方向上的位置,并将结果展示在图9,其中时间t已经被特征时间无量纲化.从图中可以看到,气泡振幅和尖钉振幅都随时间不断地增大,并且尖钉振幅的增长速度大于气泡的增长速度.此外,还可以发现,随着Re数的增大,气泡振幅和尖钉振幅在演化前期几乎不受影响,而在演化后期,气泡振幅和尖钉振幅随着Re数的增大而增大,这是由于在演化前期,不稳定性较弱,流体与流体剪切力较小,而在演化后期,不稳定性较剧烈,流体与流体间的剪切力较大.作为对比,我们还将He等[3]的结果和Li等[15]的模型的计算结果列在图9.可以看到,本文数值模拟获得的尖钉和气泡位置在演化前期与文献模型计算的结果相吻合,而在演化后期,本模型计算结果与文献模型结果有一定的差异.这是由于He等未考虑界面力的影响以及Li等未准确地处理界面力的尺度效应所造成的.

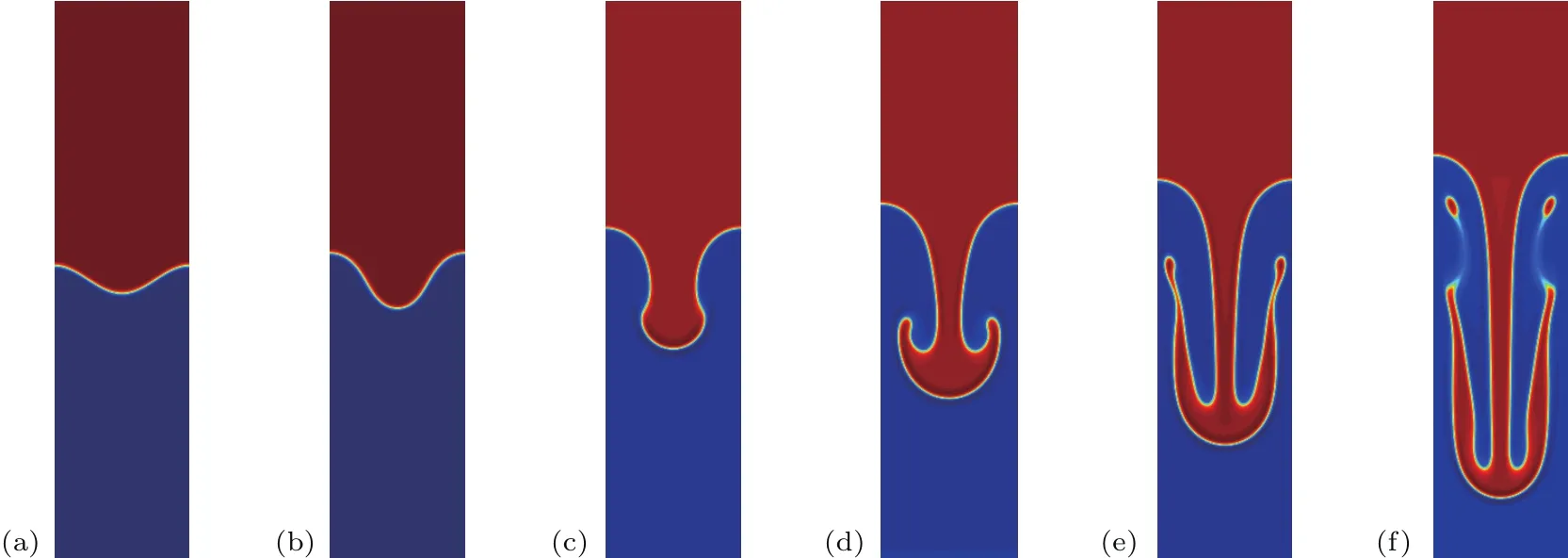
图6 Re=256时,本模型计算获取的RT不稳定性演化图 (a)t=0;(b)t=1;(c)t=2;(d)t=3;(e)t=4;(f)t=5Fig.6.At Re=256,time evolution of RT instability obtained by the present model:(a)t=0;(b)t=1;(c)t=2;(d)t=3;(e)t=4;(f)t=5.

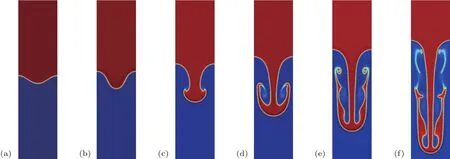
图7 Re=1024时,本模型计算获取的RT不稳定性演化图 (a)t=0;(b)t=1;(c)t=2;(d)t=3;(e)t=4;(f)t=5Fig.7.At Re=1024,time evolution of RT instability obtained by the present model:(a)t=0;(b)t=1;(c)t=2;(d)t=3;(e)t=4;(f)t=5.

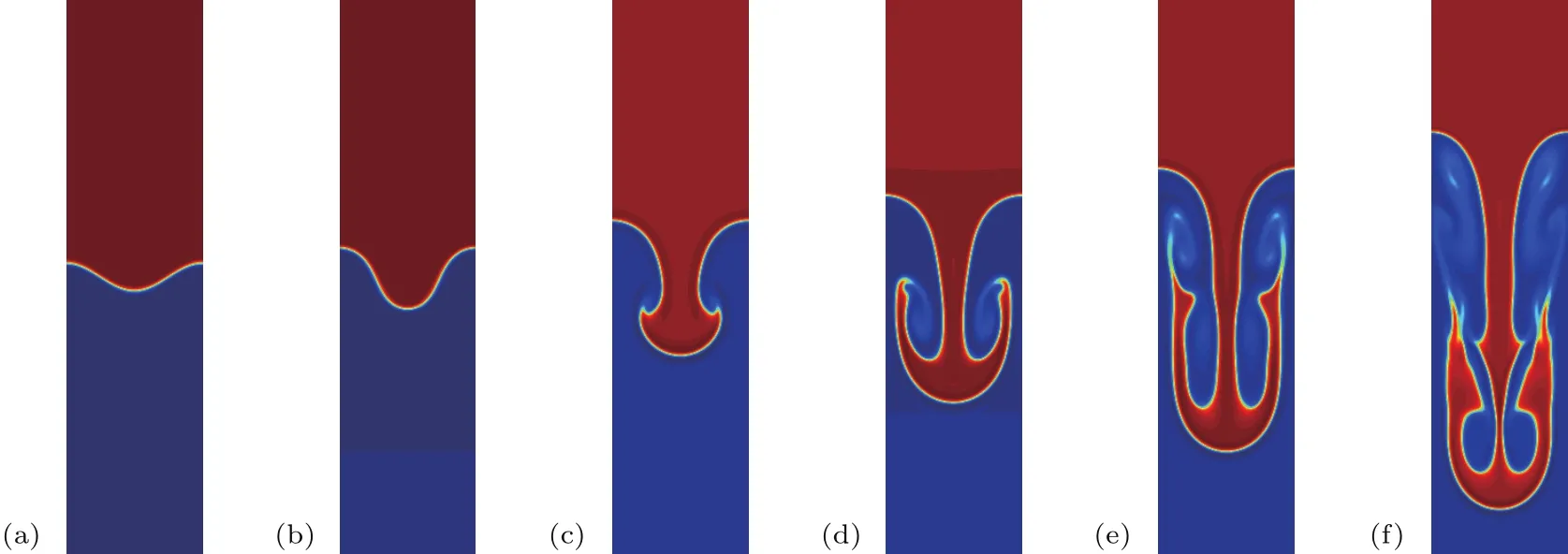
图8 Re=1024时,Li等[15]模型计算获取的RT不稳定性演化图 (a)t=0;(b)t=1;(c)t=2;(d)t=3;(e)t=4;(f)t=5Fig.8.At Re=1024,time evolution of RT instability obtained by model of Li et al.[15]:(a)t=0;(b)t=1;(c)t=2;(d)t=3;(e)t=4;(f)t=5.

图9 不同Re数下随时间演化的(a)气泡和(b)尖钉在y方向上的位置Fig.9.Time evolution of y coordinate of(a)bubble and(b)spike poistions at different Re.

通过文献调研表明,对RT不稳定性问题的研究绝大多数为单模情形,针对随机扰动的多模RT不稳定性的研究则相对较少[20].本文的最后,我们将利用修正的两相流相场LB模型对随机扰动的多模RT不稳定性进行模拟,并研究Re数对相界面演化的影响规律.物理问题设定为一个L×L的计算区域,对两相界面处施加一个初始的微小扰动,其中扰动函数给定为

其中,an和bn是满足高斯正态分布的随机数,序参数的初始分布则给定为

在数值模拟中,一些物理参数设置如下:ρl=3,ρg=1,ϕl= −ϕg=1,L=512,=0.08,D=4,σ=0.0001.

首先模拟Re=4096的情形,其对应的流体黏性为0.01.图10给出了Re=4096时多模RT不稳定性中密度界面随时间演化的图案,其中时间t是被特征时间无量纲化的时间.从图中可以看到:初始阶段,扰动随时间逐渐发展:轻流体和重流体相互渗透,并在t=1时刻形成一排“蘑菇”形状;紧接着,一排“蘑菇”继续增长,变得纤细而修长(如图t=2);当t>2时,流体与流体间的剪切力变得非常大,非线性程度在加剧,造成了流体界面的混合程度在不断地加强,最终形成了非常复杂的混沌界面结构.作为对比,我们进一步模拟了Re=1024的情形.图11给出了Re=1024时多模RT不稳定性中密度界面随时间的演化图.从图中可以看出:在初始时刻,不稳定性发展的比较缓慢,界面处于抑制状态,未观察到显著的“蘑菇”形状;接着不稳定性进入稳定期,流体混合程度在降低;而在演化后期,在两相系统中也观察到较为混乱的相界面图案.最后,还模拟了Re=700的多模RT不稳定性问题.图12给出了Re=700时多模RT不稳定性中密度界面随时间的演化图.从图中可以发现初始的不稳定性发展极其缓慢,最终形成的的流体界面相对光滑,未观察到明显的混沌现象.

图10 Re=4096时,多模RT不稳定性的演化 (a)t=0;(b)t=1;(c)t=2;(d)t=3;(e)t=4;(f)t=5Fig.10.Time evolution of a multiple-mode RT instability at Re=4096:(a)t=0;(b)t=1;(c)t=2;(d)t=3;(e)t=4;(f)t=5.

图11 Re=1024时,多模RT不稳定性的演化 (a)t=0;(b)t=1;(c)t=2;(d)t=3;(e)t=4;(f)t=5Fig.11.Time evolution of a multiple-mode RT instability at Re=1024:(a)t=0;(b)t=1;(c)t=2;(d)t=3;(e)t=4;(f)t=5.

图12 Re=700时,多模RT不稳定性的演化 (a)t=0;(b)t=1;(c)t=2;(d)t=3;(e)t=4;(f)t=5Fig.12.Time evolution of a multiple-mode RT instability at Re=700:(a)t=0;(b)t=1;(c)t=2;(d)t=3;(e)t=4;(f)t=5.

4 结 论

本文基于Cahn-Hilliard相场理论提出了一种修正的两相流LB模型,通过引入新的简化的外力项分布函数,解决了界面力的尺度与多尺度分析结果不一致的问题,并且通过Chapman-Enskog理论分析,可以证明本模型能够准确地恢复到CH方程和NS方程.通过模拟一系列经典两相流的数值算例,包括静态液、液滴合并、亚稳态分解和RT不稳定性问题,用于测试本模型的准确性和可行性.对于静态液滴算例,发现当前的相场LB模型能准确地求解相界面,并且可以获得量级为10−9极小的虚假速度.还模拟了两个液滴在表面张力作用下的合并问题,获得了与前人文献相一致的数值结果:当液滴间距小于两倍的界面厚度时,液滴在表面张力的作用下自动发生合并;而当液滴间距大于两倍界面厚度,液滴不会发生合并现象.针对亚稳态分解问题,我们利用本文相场LB模型可以成功地捕获相界面的分离过程,并发现增加表面张力σ不影响界面的演化图案,但可以加速相分离进展.最后,利用本文修正的两相流相场LB模型模拟了单模的RT不稳定性问题和随机扰动的多模RT不稳定性问题,并分析了Re数对相界面的演化规律的影响,结果表明本模型可以准确地追踪单模RT不稳定性中尖钉与气泡的演化规律.另外,针对多模情形,发现高Re数时,流体界面在演化前期形成一排“蘑菇”形状,而在演化后期,流体界面则形成非常独特的混沌拓扑结构;而当Re数较低时,流体界面则相对比较光滑,演化后期未观察到非常混沌的混合现象.最后,本文对界面力的分析思路可以推广到基于Allen-Cahn相场理论的LB方法中.相比界面追踪的Cahn-Hilliard方程,基于Allen-Cahn方程的LB方法[9,21]在求解相界面方面具有较小的数值耗散,从而可以应用于大密度比两相流问题.