非高斯粗糙表面的弹性微滑接触问题研究

谢晓东，赵三星

（武汉科技大学 机械自动化学院，湖北 武汉 430081）

1 引言

微滑接触是指在摩擦接触中，当接触体受到法向力和切向力的作用，但是切向力不足以使接触体发生宏观的滑动时，在接触面间会产生微滑区域和粘着区域。微滑区域表示接触体在外加载荷的作用下发生相对微小滑移的区域；粘着区域则表示接触体在外加载荷作用下没有相对移动的区域。

文献[1-2]最早建立了弹性微滑接触的力学模型。他们假定在微滑区域的局部切向力大小等于最大静摩擦力，通过弹性力学理论分析得到了微滑接触的解析解。文献[3]进一步总结了Cattaneo-Mindlin的线接触微滑模型。文献[4-5]又分析了粗糙表面对于微滑接触的影响，但是所用的粗糙表面都是规则粗糙表面。

上述对于微滑接触的研究都是仅限于同质接触，即两个接触体的材料相同。对同质微滑接触来说，切向应力的变化对弹性变形不会产生影响。而对于异质微滑接触，切向应力的变化会对弹性变形产生影响，此时微滑接触就不符合Cattaneo-Mindlin接触问题。文献[6]最早用数值方法进行耦合求解异质微滑接触问题，得到了刚性平底压头接触问题的数值解。文献[7-8]又首次将共轭梯度法（CGM）用于同质和异质微滑接触中的应力求解，加快了计算过程。主要分析粗糙表面对于接触应力产生的影响，所以采用同质接触来简化计算模型。

半解析法被用来求解这里的微滑接触问题，即利用解析的方法求得影响系数，然后通过叠加原理，得到数值解。具体过程：通过格林函数推导出应力-应变的影响系数[12]。影响系数等于单位应力的作用下产生的应变，这样只需在意计算区域的网格划分，节省了计算时间。最后通过应力叠加得到应变。在计算过程中采用快速傅里叶变换方法（FFT）[9]和共轭梯度法（CGM）[10]，这可进一步加快计算过程，节省计算时间。

对于实际中的工程接触问题大多数都是粗糙表面接触，而粗糙表面多数符合非高斯分布。将非高斯表面叠加到微滑接触中，使接触问题更加的接近于实际。通过选取不同参数的粗糙表面，来分析非高斯粗糙表面对接触应力的影响。

2 理论模型

采用的弹性微滑接触模型，如图1（a）所示。上面为一个弹性球体，弹性模量和泊松比分别为E1，V1，下面为半空间，弹性模量和泊松比分别为E2，V2。弹性球体受到三个方向的力：法向力W和切向力Fx，Fy，在接触面间分别产生法向压力p和切向应力qx和qy。

图1 三维接触微滑模型和接触变量Fig.1 3-D Contact Model and Variables Under Partial Slip Conditions

接触表面间的接触间隙满足如下方程式：

式子：g—接触表面间隙；h0—初始刚体间距；δz—接触对在z方向

的两个表面的刚体位移；uz—接触对在z方向的弹性位移。

当受到法向力作用时，根据接触力学[12]中的理论分析，接触表面点（x，y）处的弹性位移uz可以表示为：

式中：M、N—离散化后 x，y 方向的网格数；（i，j）—离散化坐标；p—接触面间的压力；K—应力-应变影响系数，等于单位法向压力作用下的表面变形，可以通过格林函数插值求解[12]。为了节省计算时间，采用快速傅里叶变换方法（FFT）[11]来计算弹性位移。

在接触问题中接触压力和接触间隙需要满足如下边界条件：

在接触区域内：

根据上述条件可以知道接触问题实际上变成了线性补余问题，将式（1）写成如下形式：

式中：hi—常数矩阵，而Kp—弹性变形。

通过变分原理将式（6）转变为二次函数的条件极值问题，即寻找函数：在约束条件式（4）和式（5）下的条件极值，然后就可以应用共轭梯度法来求解[13]。

文献[12]总结了微滑接触的理论模型，如下所示：

式中：ux，uy—接触对在 x，y 方向的弹性位移；δx，δy—接触对在 x，y方向两个表面的刚体位移；Sx和Sy—接触对沿x，y方向的相对滑移距离。以上的各个变量的实际意义已经详细表示在图 1（b）中。

由于接触面间的初始应力分布已经从式（1）中的纯法向接触求解得到，所以上述微滑模型可以简化为：

式（8）和式（9）中x，y方向的弹性位移可以根据

如下公式求解

式（10）中的 m 可以是 x或者 y，Kmx，Kmy，Kmz分别表示 x，y，z方向的单位切向应力和单位接触压力作用下产生的切向位移[12]。同样，对式（10）的计算可以采用FFT算法，以节省计算时间。

切向应力qx，qy和滑移距离Sx，Sy在粘着区域和微滑区域要遵循如下边界条件：

粘着区：

式（11）和式（12）中的μf表示摩擦系数，这样式（9）的微滑模型就可以通过共轭梯度法求解[7]。

为更接近于实际，研究了粗糙表面弹性微滑接触问题。首先，基于参考文献[11]中的方法生成非高斯粗糙表面，文献中比较了数值方法生成粗糙表面和实际粗糙表面，两个表面具有高度的一致性。之后，采用上述方法对粗糙表面微滑接触问题进行分析。

3 计算结果与比较

3.1 算法验证

首先计算不考虑粗糙度的光滑表面微滑接触，来验证算法的正确性。根据表1中的球-面微滑接触实际数据和这里的算法得到了如图2所示的切向应力的数值解，通过与解析解[3]相比较，发现数据和图形几乎完全一致，即证明了这里算法的可靠性。图中的qx和ph分别表示切向应力和最大赫兹接触应力，a表示赫兹接触半径。

表1 输入参数Tab.1 Input Parameters

图2 切向应力在y=0处的分布Fig.2 Tangential Stress Distribution in y=0

3.2 粗糙表面微滑接触

求解粗糙表面的微滑接触问题，首先要生成接近于实际工况的非高斯粗糙表面。生成粗糙表面所采用的网格为（128×128），粗糙表面的数据为：各向同性粗糙表面x和y方向的波长βx和βy都为 20μm，RMS为 0.1μm，偏态 SK 的分别为取值 0.0、0.5、1.0、1.5。峰度 K 的取值范围为（3～10）。

由于非高斯粗糙表面生成具有随机性，所以本文对于同一参数的粗糙表面分别生成十个，并分别计算求解了最大应力，最后取平均值，以期获得可靠的接触规律。

在粗糙表面接触问题，最大表面应力是机械零部件的界面破坏分析和使用寿命设计的一个重要参考指标。在不同峰度和正偏态粗糙表面下的最大切向应力和最大接触压力（球-面微滑接触参数见表1），如图3所示。从图中可以看出：对最大切向应力，偏态一定，峰度对最大切向应力的影响较小。随着峰度的增加，最大切向应力基本保持不变；如果峰度一定，随着偏态的增加，最大切向应力减小。对最大接触压力，偏态一定，随着峰度的增加，最大接触压力逐渐增加，如果峰度一定，随着偏态的增加，最大接触压力减小。

图3 不同的峰度和正偏态对最大切向应力和最大接触压力的影响Fig.3 The Influence of Different Positive Skewness and Kurtosis to Maximum Tangential Stress and Maximum Pressure

上面所讨论的粗糙表面都是正偏态表面，而负偏态的表面也广泛存在于生产实际中，不同峰度和负偏态的粗糙表面对最大应力产生的影响，如图4所示。从图4中可以看出：对最大切向应力，负偏态的变化对最大切向应力的影响较小。峰度一定，随着偏态的变化，最大切向应力基本保持不变。对最大接触压力，峰度一定，随着偏态减小，最大接触压力也随着减小。

图4 不同的峰度和负偏态对最大切向应力和最大接触压力的影响Fig.4 The Influence of Different Negative Skewness and Kurtosis to Maximum Tangential Stress and Maximum Pressure

正负偏态对最大应力的影响情况，如图5所示。从图5中可以看出：峰度一定，负偏态的最大切向应力和最大接触压力要比正偏态的情况下都要大。同时，正负偏态的最大接触压力和最大切向应力随峰度的变化趋势基本一致。

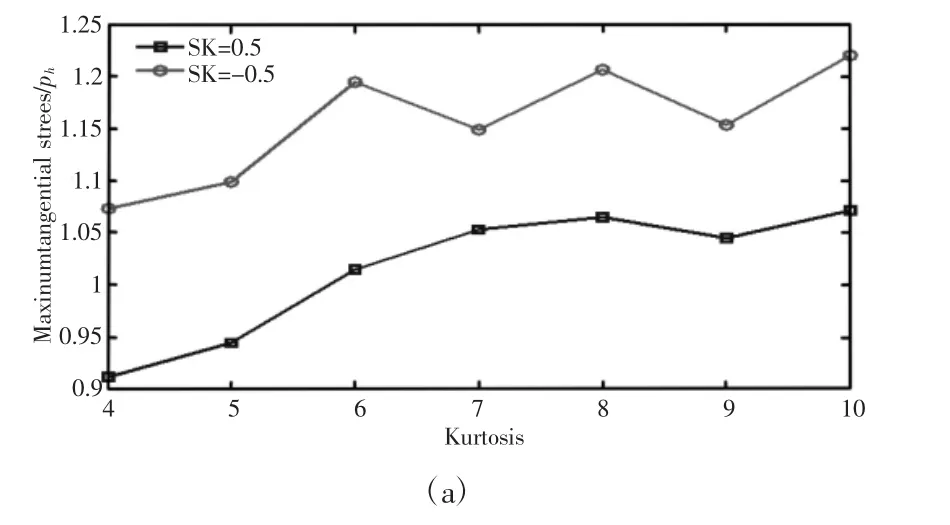
图5 正负偏态粗糙表面对最大切向应力和最大接触压力的影响对比Fig.5 The Influence of Positive and Negative Skewness on the Maximum Tangential Stress and Maximum Pressure

粗糙表面除了各向同性表面还存在着各向异性表面。所谓各向异性粗糙表面就是表面的波长βx和βy不再相等，此处取x，y方向的波长分别为20μm和200μm，其他参数不变。各向同性和各向异性粗糙表面的最大应力，如图6所示。可以看出：在相同的峰度和偏态条件下，各向同性与各向异性粗糙表面的最大表面应力比较接近。各向同性和各向异性的最大切向应力基本一致；各向同性的最大接触压力略大于各向异性。

图6 各向同性和各向异性粗糙表面对最大切向应力和最大接触压力的影响Fig.6 The Influence of Isotropic and Anisotropic Rough Surface to Maximum Tangential Stress and Maximum Pressure

4 结论

通过半解析法结合快速傅里叶变换（FFT）和共轭梯度方法（CGM）求解微滑接触问题。将不同峰度和偏态的非高斯粗糙表面叠加到接触面，分析最大接触压力和最大切向应力的变化情况，得到如下结论：

（1）对于固定的正偏态，随着峰度的增加，最大接触压力也随着不断增加，但是最大切向应力基本保持不变。对于固定的峰度，随着正偏态的增加，最大接触压力和最大切向应力反而减小。

（2）对于负偏态粗糙面，偏态值的变化对于最大切向应力的影响较小；对于固定的峰度，随着负偏态的减小，最大接触压力也随之减小。同时，负偏态的最大切向应力和最大接触压力要比正偏态下大。

（3）各向同性和各向异性粗糙表面的最大切向应力和最大接触压力比较接近。在相同的偏态和峰度条件下，最大切向应力基本保持不变。各向同性的最大接触压力略大于各向异性。