一种图像矢量化中的圆弧拟合方法

杨延竹，袁秀泰，韩阜益

（1.东华大学 机械工程学院，上海 201620；2.东华大学 资产管理处，上海 201620）

1 引言

在对图像进行矢量化的过程中，对于简单图形目前多采用若干折线段进行拟合的方式，但针对复杂图形，如存在圆弧，或复杂的非圆曲线等，用直线对曲线进行拟合只能大致反映曲线的方向，不能客观地反映曲线的特征，而且直线拟合形状精度不高，不能很好的反应轮廓特征，在拟合时如果曲线局部曲率较大，则会造成该部分直线段较多而短，造成机器手频繁地启动和停止，影响切割效率。

针对上述问题，很多研究人员将直线拟合与圆弧拟合相结合，进行了充分研究并且收获了一定成果。采用混合圆弧—直线逼近法逼近原始轮廓的方法，用样条曲线拟合轮廓曲线，用圆弧—直线逼近法逼近拟合的曲线，并重新离散化机器手加工点，减少了机器手走刀数，提高了加工效率[1]。不过这种方法只适合一条曲线，对于存在断点的连续的多条曲线则不适用。还有基于遗传算法的相切圆弧逼近曲线算法[2]；使用双圆弧拟合非圆曲线的算法[3]。然而这两种算法都比较复杂，实际应用效果较差。还可以利用垂直平分线求交法对曲线进行圆弧拟合，即利用圆内接多边形的任意一条线段都通过圆心的原理，将满足圆弧拟合条件的折线段进行圆弧拟合[4-5]。采用最小二乘法对圆弧进行拟合的算法[6-7]，利用这种方法得到的圆弧，是采样点的最优解，即最佳逼近圆。

上述方法都可以得到逼近原始轮廓的最佳圆弧曲线，但是原始轮廓的起始点和终止点很有可能不会落在拟合的圆弧曲线上，造成现象，如图1所示。即拟合后的两段相邻的圆弧或圆弧与直线段之间会出现交叉、没有交点等状况，造成机械手在跟踪识别完第一条圆弧曲线后，找不到下一段圆弧或者直线的起点，导致机器手误判或者丢步，无法完成后续的切割。

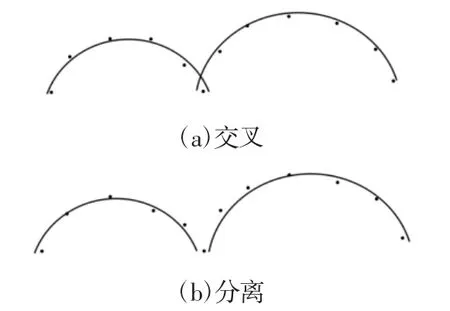
图1 交叉和分离现象Fig.1 Phenomenon of Intersectional and Separated

在前人各种研究成果的前提下，结合实际情况，在最小二乘法的基础上，对拟合的圆弧进行了微小的平移和改动，保证圆弧每段圆弧的起始点和终止点都落在拟合后的圆弧上。这样既对原始轮廓有了很好的保形，保证了加工精度，使轮廓更加平滑，也使机器手能够连续工作，不会出现误判或者丢刀等现象，提高了加工效率。

2 圆弧拟合算法

在进行圆弧拟合前，首先要对折线段进行判断其是否符合圆弧特征。因此对完成直线拟合的图像，搜索其连续的折线段，判断出符合圆弧拟合条件的折线段序列，将符合条件的折线段进行圆弧拟合。

2.1 圆弧搜索

对于线条轮廓图像，判断连续的直线段能否可以构成一段圆弧，一般遵循如下规则[8]：

（1）两条相邻的折线段的夹角要在规定的范围之内。这是因为：首先，人眼在观察一副图片时，对夹角小于90°的部分最容易发现，因此具有该特征的部分不能被拟合为圆弧。另外，夹角越大的两条折线段，被拟合的圆弧和实际图形越匹配。

（2）按照同一矢量化方式，获得的圆内接多边形应该近似为等边多边形或其中连续的几条边，因此，各折线段的长度近似，各夹角近似相等。

不过，如果只根据上述两条规则，不能判断出折线段序列是否符合圆弧条件，因此，还需要引用其他条件加以限制。

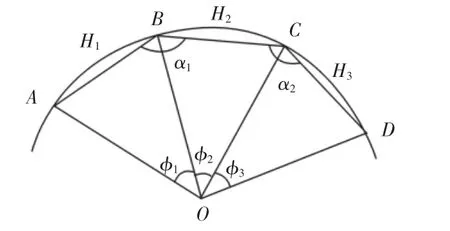
图2 弧长近似法搜索圆弧Fig.2 Approximation Method of Arc Length Search Arc

利用弧长近似法搜索圆弧[5，9]，如图 2 所示。H1，H2，H3是拟合圆 O 中三条连续的折线段，H1、H2的夹角是 α1，H2、H3之间的夹角是α2。设HAC、HBD分别是AC、BD间的距离，由余弦定理可得：

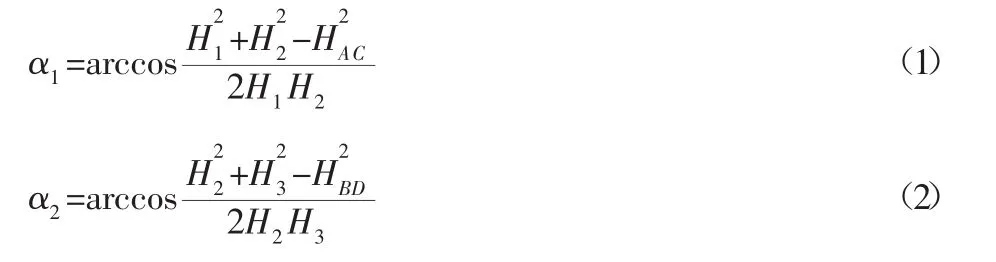
角度较小情况下，弦长与弧长近似相等，可知：

通过该规则，可以求出每两条相邻直线段对应的半径R。若求出的半径与之前求得的半径之差超过规定的范围内，就认为该直线段不属于该段圆弧，若在允许范围内，则认为新的折线段属于该圆弧，继续判断下一折线段是否属于该圆弧。

2.2 圆弧拟合算法

通过上述算法对折线段实现圆弧搜索，将符合圆弧拟合条件的折线段进行圆弧拟合。目前比较典型的圆弧拟合算法有利用垂直平分线求交法[10]和最小二乘圆拟合算法。利用垂直平分线求交法拟合圆弧的原理是从识别出的可以拟合为圆弧段的折线段中选一条为母线段，作其垂直平分线，再与其他折线段的垂直平分线求交点，获得交点的最远点PF和最近点PC，设定一矩形区域，以PFPC两点距离为矩形的高，以母线段为矩形的宽。计算该区域内每个坐标点到每个顶点的距离（即圆的近似半径），同时计算半径的平均值以及均方差。最后取使均方差最小的坐标点为该圆弧段半径，所对应的平均半径为圆弧半径。

最小二乘法是经典的数学优化算法，通过最小化误差的平方和找到一组数据的最佳函数匹配。利用最小二乘法对圆弧进行拟合的核心思想是：获取可以拟合为圆弧的折线段顶点坐标数据，根据误差平方和最小化原则，找出这些数据的最佳函数匹配，即最佳拟合圆。其数学原理为：给定一组圆弧坐标点（xi，yi）（i=1，2，…n），已知圆曲线方程：

圆弧坐标点（xi，yi）到圆心的距离为：

点（xi，yi）到圆心的距离的平方与半径的平方求差：

通过求δi的平方和的极小值可以求得待定系数a，b，c，从而求出圆弧的圆心坐标及半径的最优解，使该函数的误差平方和最小。

上述两种拟合方法从不同角度实现了圆弧的拟合，都具有一定的实用性。但这两种方法都有其局限性和各自的缺陷。利用垂直平分线求交法中对母线段的选择非常关键，而且由于要对区域内的所有坐标点进行分析，计算量较大。两种方法虽然能计算出圆弧的圆心与半径，但都只能拟合出圆而非圆弧，由于拟合圆为该圆弧段坐标点的最优解，因此折线段的起始点和终止点很有可能不会落在拟合的圆上，这将导致机器手无法找到起始点而无法运行或者出现丢刀等现象。综合上述结论，考虑实际加工要求，在最小二乘法拟合圆的基础上，对拟合的圆弧或者圆进行了微小的平移和改动，使其能够在满足切割要求的前提下，有效地解决上述问题。

3 改进的最小二乘圆弧拟合算法

为使后续的机器手轨迹行程更加简单高效，便于路径规划，保证机器手在运行时连续而不出现间断。在圆弧拟合时，应保证待拟合折线段的起始点和终止点在拟合的圆弧上，即圆弧的端点确定。针对这一约束性要求，改进方法的基本思路是：在满足机械手加工精度要求的前提下，从机械手的实际切割工艺出发，保证待拟合为圆弧的折线段的起始点和终止点落在圆弧上为约束条件，约束最小二乘圆弧的拟合，保证拟合出的图形连续不会出现间断或交叉。

首先，用经典最小二乘法求出待拟合圆弧的半径R和圆心O（x，y），具体算法前面已经说明，在此不再赘述。要使两端点落在拟合圆弧上，即要求两端点到圆心的距离为半径，设起始点为P1，终止点为P2，根据圆心到圆弧上的任一点的距离都为半径的原理，我们假设P1，P2在拟合的圆弧上，连接两端点P1P2，作其垂直平分线L，以P1（P2）为圆心，R为半径作圆交垂直平分线L于O1，O2两点。比较O1，O2两点到圆心O的距离，判定距离较近的一点为新的圆心O′。可以看出，改进的算法保有了经典最小二乘法拟合出的半径R，而对圆心的位置进行了适当的改变，即将整个圆进行了微小的平移，平移的距离一般不会超过2个像素，反应到实际中不会超过1mm，在精度要求并不高的加工生产中，这类误差完全在允许范围内，但这种方法保证了圆弧的端点落在拟合的圆弧上。

在对圆弧进行拟合时，还要确定圆弧端点与圆心的关系。通过上述算法求得拟合圆弧的圆心坐标及半径，且圆弧端点坐标已知，圆心及端点坐标是二值图像中的像素坐标，也是绝对坐标。通过绝对坐标求圆心和端点的相对坐标关系，以圆心O为原点，像素坐标的x方向为新的坐标系的x方向，像素坐标的y方向为新的坐标系的y方向建立直角坐标系，以x正半轴为始边，沿逆时针方向旋转，判断向量O′P1，O′P2与x正半轴的夹角，通过这种方式，确定两端点的相对方位，实现对圆弧的拟合。

仅确定圆弧端点的相对方位不能实现圆弧的正确拟合，还要知道圆弧的旋转方向，有的圆弧是按照顺时针方向拟合，而有的是按照逆时针方向拟合。正确的拟合方式应该是从圆弧起始点按照逆时针旋转进行拟合，在没有规定其旋转方向的情况下，就有可能出现其沿顺时针方向拟合，导致拟合错误，如图3所示。

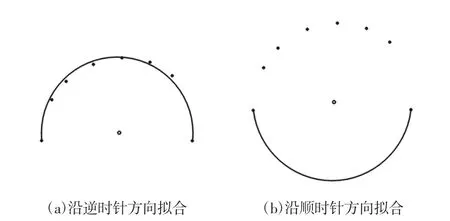
图3 按照不同旋转方向拟合的圆弧Fig.3 Different Direction of Rotation of Arc Fitting

对折线段进行圆弧拟合至少需要两段及以上的连续折线段，即至少3个以上的有序坐标点，在判断圆弧的旋转方向时，将第二个坐标点S作为参考对象。同样，用确定端点方位的方法确定点S的方位，如图4所示。比较∠P1O′X和∠SO′X，若∠P1O′X＜∠SO′X，则令圆弧沿逆时针方向旋转，若∠P1O′X＞∠SO′X，则令圆弧沿顺时针方向旋转。

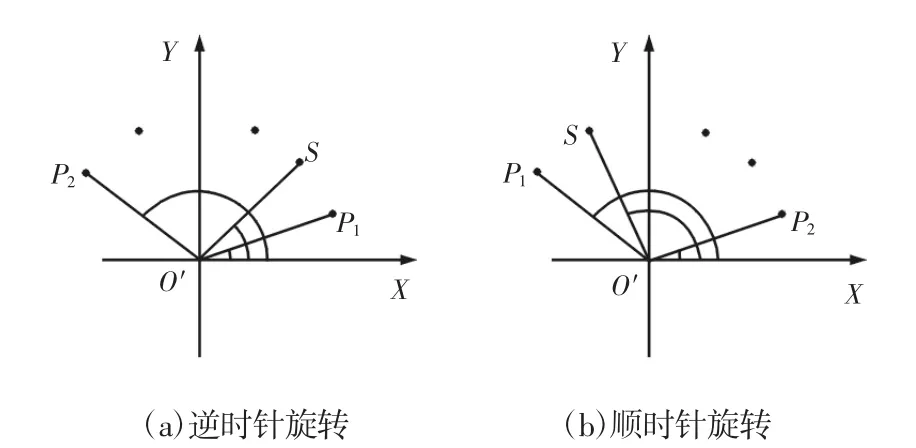
图4 圆弧旋转方向Fig.4 Direction of Arc Rotation

但有时还会遇到，如图5所示。很明显，圆弧应从逆时针方向拟合，但此时∠P1O′X＞∠SO′X，按照上述方法，其将按照顺时针方向拟合，导致拟合错误。因此，在拟合时，将起始点P1，第二个坐标点S，终止点P2三点进行比较。

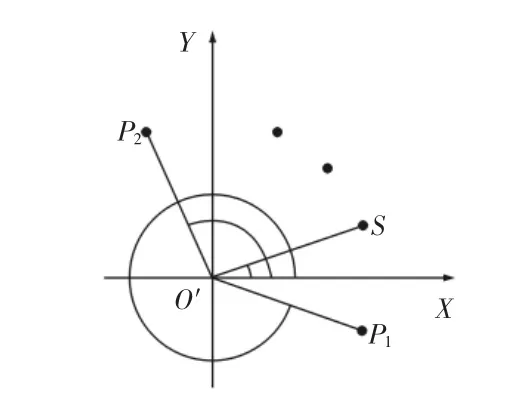
图5 错误拟合Fig.5 Error of Fitting

当∠P2O′X 介于∠P1O′X 和∠SO′X 之间时，即 min（∠P1O′X，∠SO′X）＜∠P2O′X＜max（∠P1O′X，∠SO′X），此时再按照上述分析方法确定正确的拟合方向。

当∠P2O′X＜min（∠P1O′X，∠SO′X）或者∠P2O′X＞max（∠P1O′X，∠SO′X）时，令

min′（∠P1O′X，∠SO′X）=min（∠P1O′X，∠SO′X）+2π，同样再按照上面的分析方法进行分析比较，确定拟合方向。

通过此种方法，包含了所有可能出现的情况，实现圆弧的正确拟合。

4 实验对比分析

分别采用经典最小二乘法与提出的方法拟合圆弧，如图6所示（a线为经典最小二乘法拟合结果，b线为改进的算法拟合结果），相对于经典最小二乘法，通过改进的算法发生了微小的移动，但保证了圆弧的端点落在圆弧上。

图6 两种不同算法拟合效果图Fig.6 Two Different Fitting Rendering Algorithm

在多段连续的圆弧上，经典最小二乘法在两段圆弧相接处会出现间断以及交叉的现象，而通过这里的方法解决了这一问题，如图7所示。

图7 多段连续圆弧拟合结果Fig.7 Multistage Continuous Arc Fitting Results

5 结论

在经典最小二乘法拟合圆的基础上，针对机器手实际运动特点，对拟合的圆弧进行了微小的改动或平移，保证可以拟合为圆弧折线段序列中的第一条折线段的起点和最后一条折线段的终点落在拟合后基于圆心约束最小二乘圆拟合的短圆弧测量的圆弧上。与经典的最小二乘法相比，这里的方法并没有对圆弧进行巨大的改动，使其在误差允许范围内，对原始图案实现了高度的保形，拟合后的轮廓更加平滑。使机器手能够连续跟踪识别而不出现间断或者丢刀现象，有效地提高了切割效率。