基于有限测试数据的结构响应不确定性量化分析

骆勇鹏，黄方林，刘景良，鲁四平，许旭堂



基于有限测试数据的结构响应不确定性量化分析

骆勇鹏1，黄方林2，刘景良1，鲁四平2，许旭堂1

(1. 福建农林大学 交通与土木工程学院，福建 福州 350108；2. 中南大学 土木工程学院，湖南 长沙 410075)

针对实际工程中的实测数据往往有限，其服从的概率分布函数难以确定的问题，现有的不确定性分析方法常需假设参数服从某种概率分布后进行随机分析。当假设的概率分布与实际不符时，会产生较大的误差。为此，提出一种适用于概率分布函数未知和小样本数据的结构响应不确定性分析方法。该方法基于小样本数据，采用Bootstrap抽样和AIC准则来确定参数的最优概率分布函数和分布参数，通过随机抽样并将样本数据代入响应面模型计算结构响应，从而快速量化参数变异对响应不确定性的影响。以数值算例探讨原始样本个数及抽样次数对分析结果的影响，建议运用所提方法进行结构响应不确定性分析时，原始样本个数至少为30个，抽样次数可取1 000次以上。采用斜拉桥动力响应不确定性分析来验证所提方法在实际工程分析中的应用可行性及可靠性。研究结果表明：所提方法不需要事先假设不确定性参数的概率分布函数及分布参数，仅利用少数样本数据即可完成结构响应不确定性分析。

不确定性分析；小样本数据；灵敏度分析；响应面；Bootstrap抽样

基于响应面和Monte Carlo的结构不确定性分析方法是目前不确定性分析中应用较为广泛的方法之一。其思想是假设参数服从某种概率分布，通过对样本进行抽样，然后输入到响应面中，计算对应的输出值进而获得输出的统计特性，避免多次有限元计算过程，有效地提高了计算效率[1−3]。然而，该方法也存在一定的限制，既实际工程中的实测数据往往有限，其服从的概率分布函数难以确定。当假定的概率分布函数与实际不符时，将产生较大的误差，从而影响对结构实际服役性能的判断[4]。也有学者提出可用K-S检验等方法来确定不确定性参数的概率分布[5]。当样本个数较大时，此类方法可行，但当样本数量较少时，所确定的概率分布本身具有一定的不确定性，此时基于Monte Carlo法的不确定性分析方法可能产生新的误差[6]。为此，提出一种适用于概率分布函数未知情况下，基于小样本数据的结构响应不确定性量化分析方法。该方法首先基于Bootstrap抽样和赤池信息准则(Akaike Information Criterion, AIC)来确定不确定性参数的最优概率分布及分布参数。然后，根据参数所服从的最优概率分布进行随机抽样，将随机样本代入响应面模型，计算各组样本所对应的响应值并进行统计分析得到结构响应的统计特征，从而实现结构动力不确定性量化分析。采用数值算例和斜拉桥动力响应不确定性计算来验证所提方法的可行性及可靠性，并探讨材料参数、构件尺寸不确定性对结构动力响应不确定性的影响。

1 基于小样本数据的结构响应不确定性量化分析

结构动力不确定性量化的主要研究工作包括不确定性分析和灵敏度分析。前者对应于量化输入不确定性通过物理系统传递给输出的不确定性，后者是定量单个参数的不确定性对输出不确定性的影响程度[7]。目前的研究大多集中于输出不确定性的量化，较少关注单个参数不确定性对输出不确定性的影响。此外，在工程领域中如何基于小样本数据进行不确定性分析的研究也较为少见。

本文提出的适用于概率分布函数未知情况下，基于小样本数据的结构响应不确定性分析方法主要包括3个部分：最优概率分布函数及分布参数确定、不确定性灵敏度分析及不确定性分析。现分别进行阐述。

1.1 最优概率分布函数及分布参数确定方法

如前所述，参数概率分布函数的正确与否对结构不确定性分析的可靠性有较大影响。在样本个数很小的情况下准确计算出不确定性参数所服从的概率分布函数是难以实现的。因此，如何在小样本数据下确定不确定性参数所服从的最优概率分布函数和分布参数来保证不确定性分析结果的准确是基于小样本数据的结构响应不确定性分析的一种解决途径。

Bootstrap法运用模拟再抽样技术代替理论分析，基于有限的试验观测数据模拟再抽样出大量符合原数据特征的模拟样本，提供足够的样本进行概率统计分析[8−9]，避免对概率分布函数假定的依赖。为此，结合AIC准则[10]，将Bootstrap引入最优概率分布函数及分布参数的确定中。该方法的计算流程如下：

3) 构造统计量

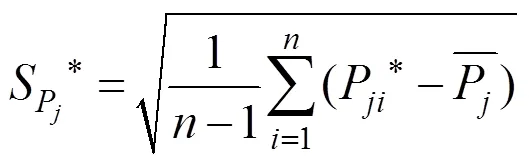
4) 独立重复步骤2) 至步骤3)次，得到个统计量值，最后根据式(5)和式(6)计算第个参数的均值和标准差，作为概率分布函数的分布参数。

基于每个Bootstrap子样本计算的备选概率分布函数的AIC值，次抽样即可得到个最优概率分布函数，为了能够确定不确定性参数的最优概率分布函数，定义最优概率分布函数指标，表达式如下：

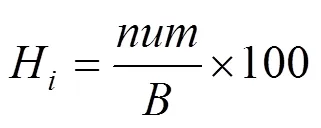
式中：为备选概率分布函数被识别为最优概率分布函数的次数。通过比较的值，选择最大的概率分布函数作为不确定性参数的概率分布函数。此时，不确定性参数所服从的最优概率分布函数及分布参数就可确定。

1.2 灵敏度分析及不确定性分析

为了提高响应不确定性量化分析的计算效率，引入响应面理论来代替有限元模型进行传递分析。交替条件期望算法(alternating conditional expectation，ACE)算法[11]不需要事先假定响应面模型的表达式，可以避免因事先指定的响应面型式无法准确描述参数与响应之间复杂的关系而产生的误差，因此本文采用该方法进行响应面拟合。

首先初步确定不确定性参数，采用均匀实验设计方法进行实验设计。根据均匀设计表进行试验设计并计算相应试验点的结构响应，采用ACE非参数回归方法确定各个参数的最优变换函数关系，建立ACE响应面。该算法的具体实现可参阅文献[12]。

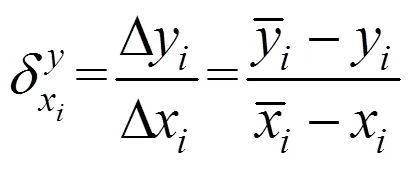
在确定各个参数变异对结构动力不确定性的影响程度后，选择灵敏度因子较大的参数作为输入，根据不确定性参数所服从的概率分布进行随机抽样得到一系列的样本，代入ACE响应面中，通过插值计算即可快速计算各组样本所对应的结构动力响应，通过概率统计分析即可得到结构响应的统计特征值，达到结构响应不确定性量化分析的目的。

1.3 原始样本个数、Bootstrap抽样次数对最优分布函数及分布参数的影响

通过计算机编程，生成200个满足均值为2，标准差为0.01的正态分布数据作为实测数据，研究原始样本个数对确定最优分布函数及分布参数的影响。

1.3.1 原始样本个数对最优分布函数及分布参数的影响分析

为了研究原始样本个数对最优分布函数及分布参数的影响，分别选择200个数据的前10，20，30，40，50和100个数据来模拟原始样本数据。以正态分布函数、威布尔分布函数及极值I分布为备选概率分布函数，Bootstrap抽样次数为1 000。采用提出的方法确定不确定性参数所服从的概率分布函数及分布参数。

概率分布函数确定结果如图1所示。从图1可以看出，当原始样本个数为10，30和100个时，正态分布函数被识别为最优概率分布函数的概率分别为47.2%，90.7%和99.9%。由此可知，原始样本个数对概率分布函数的确定有较大影响，原始样本个数越多，概率分布函数确定越准确。

表1给出了原始样本个数对分布参数的影响分析结果。从表1可知，随着原始样本个数的增加，不确定性参数的均值误差越来越小，标准差的误差总体上也随着原始样本个数的增加而变小，但是标准差的误差相较于均值来说，还是比较大。

综合以上分析结果，考虑实际工程限制，无法获取足够多的样本数据，推荐原始样本个数为30以上，概率分布函数及分布参数的确定可满足工程精度要求。

图1 原始样本个数对分布函数的影响分析

表1 原始样本个数对分布参数的影响

1.3.2 Bootstrap抽样次数对最优分布函数及分布参数的影响分析

为研究Bootstrap抽样次数对最优分布函数及分布参数的影响，以前30个数据为原始样本数据， Bootstrap抽样次数分别为100，200，300，400，500，1 000，5 000及10 000次。再次采用提出的方法确定不确定性参数所服从的概率分布函数及分布参数。计算结果如图2和表2所示。从图2和表2可知，Bootstrap抽样次数对分布函数及分布参数的影响不大。当抽样次数为100，1 000及5 000个时，正态分布被识别为最优概率分布函数的概率分别为88%，91%和91%。随着抽样次数的增加，分布参数误差没有明显变化。结合Bootstrap抽样的特点，推荐抽样次数至少1 000次。

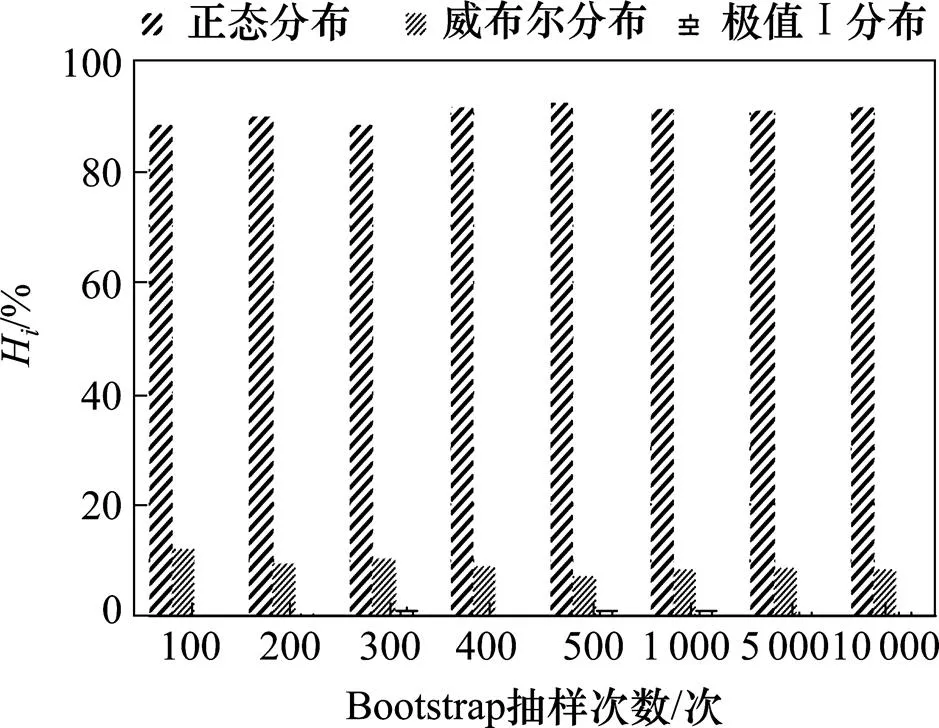
图2 Bootstrap抽样次数对分布函数确定的影响

表2 Bootstrap抽样次数对分布参数的影响

2 斜拉桥频率响应不确定性量化分析

以宁波甬江大桥主桥为研究对象，进行频率响应不确定性量化分析。宁波甬江大桥主桥为独塔竖琴型双索面的预应力混凝土斜拉桥，全长202 m，跨径布置为105 m+97 m。主塔为门式塔柱，主梁的基本断面形式是双边箱，主梁全宽 24 m，两侧的箱梁宽 6.75 m。

根据设计图纸，采用ANSYS建立该桥的空间有限元模型，其中主梁采用自定义箱形截面单脊梁模拟，桥塔采用空间梁单元Beam188模拟，斜拉索采用Link180空间杆单元模拟。全桥共2 298个单元，4 453个节点。如图3所示。

图3 有限元模型图

2.1 不确定性参数概率分布函数及分布参数确定

为了模拟实际工程测量得到的小样本数据，选取主梁弹性模量1，主梁质量密度1，主塔弹性模量2，主塔质量密度2，拉索弹性模量3，拉索质量密度3及拉索的3种截面形式的横截面积1，2和3作为不确定性参数。假设9个不确定性参数为服从以名义值为均值，变异系数为0.1的正态分布，采用LHS随机抽样方法，随机抽取30个数据作为原始样本个数，如表3所示。

以正态分布、威布尔分布及极值I分布作为备选分布函数(实际工程中可选择较多的不同概率分布函数作为备选分布函数，以提高精度)。采用所提方法计算各个备选概率分布函数被识别为最优概率分布函数的次数及分布参数，i的计算结果如图4所示。从图4可知，9个参数的最优概率分布函数均为正态分布函数，与假设的一致，说明所提方法在小样本数据下可以有效地识别不确定性参数所服从的最优概率分布函数。表3还给出了9个不确定性参数的统计特性。由表3可以看出，9个不确定性参数的样本均值与标准差误差较小。

图4 备选概率分布被识别为最优分布的次数

2.2 模态频率不确定性分析

为了能够快速计算参数变异下的结构响应，首先以9个参数为输入参数，采用均匀设计方法确定试验点，计算各个试验点所对应的前5阶模态频率1~5。采用ACE算法进行非参数回归，建立前5阶模态频率的ACE响应面。限于篇幅，仅给出第1阶模态频率的各个参数及其相应变换的映射关系图，如图5所示。表4中给出前5阶模态频率ACE响应面的拟合相关系数。由表4可知，前5阶模态频率的拟合相关系数值均接近于1，说明所拟合的前5阶模态频率的ACE响应面具有较高的精度。

表3 结构参数统计特性

图5 第1阶固有频率及9个不确定性参数与其对应的ACE变换的映射关系图

表4 前5阶固有频率ACE模型的最大相关系数值

依所服从的分布对9个不确定性参数进行随机抽样(104次)。为了考察单个参数变异对前5阶模态频率不确定性的贡献，分别将单个参数的随机样本代入ACE响应面中计算相应样本点所对应的结构前5阶模态频率的取值(其余几个参数取均值)。计算各个参数的随机样本及其对应的模态频率在置信水平为95%下的置信区间。根据式(8)和式(9)计算得到各个参数的灵敏度因子，如图6所示。从图6中可知，对于第1阶固有频率而言，主塔的弹性模量2和质量密度2灵敏度最高，均在40%以上，其余参数为不敏感参数。主梁的弹性模量1和质量密度1对第2阶固有频率至第5阶固有频率的影响程度均较大；其次是拉索的弹性模量、主塔的弹性模量2和质量密度2；拉索横截面面积2和3对第4和第5阶固有频率较为敏感，而1则对第3阶固有频率较为敏感。

为了验证以上分析结果的准确性，再次采用基于方差分析的灵敏度分析方法进行灵敏度分析，如图7所示。比较图6和图7可知2种方法计算得到的灵敏度分析结果一致，验证本方法的准确定性。但是所提方法仅利用少数样本数据即可实现，不需事先假设不确定性参数的概率分布函数及分布 参数。

以灵敏度因子较高的参数作为不确定性参数，进行随机抽样(104次)，灵敏度较低的参数取均值，共计104组样本值，分别计算各组样本所对应的前5阶模态频率。基于大样本数据对前5阶模态进行概率统计分析，计算结果如表5所示。课题组于2014年7月对该桥进行了静动力测试，模态频率实测结果也列于表5中。

图6 基于所提方法的前5阶固有频率灵敏度分析结果

图7 基于方差分析的前5阶固有频率灵敏度分析结果

表5 不确定性分析结果

从表5可知，基于确定性模型计算的模态频率小于实测值，最大误差为10.32%。所提方法计算的前五阶模态均值与实测值误差更小，最大误差为−8.41%。根据不确定性分析结果可知，当9个参数的变异系数在10%范围的情况下，前5阶模态频率的变异系数基本在5%~7%左右。实测频率在不确定性分析结果范围内，因此可认为造成实测频率与确定性模型计算的频率不一致的原因可能是实际桥梁结构的材料参数及尺寸与名义值不一致。

3 结论

1) 原始样本个数对不确定性参数的分布函数类型影响较大，建议原始样本个数30以上。Bootstrap抽样次数对概率分布类型影响不大，考虑Bootstrap抽样方法的特点，建议Bootstrap抽样次数1 000次以上。

2) 当9个参数的变异系数在10%范围的情况下，前5阶模态频率的变异系数基本在5%~7%。采用确定性模型对结构进行分析计算无法考虑不确定性的影响。而所提方法不需要事先假设不确定性参数的概率分布函数及分布参数，仅利用少数样本数据即可完成结构响应不确定性分析。

[1] XIA Z, TANG J. Characterization of dynamic response of structures with uncertainty by using Gaussian processes [J]. Journal of Vibration and Acoustics, 2013, 135(5): 6−18.

[2] Sgambi L, Garavaglia E, Basso N, et al. Monte Carlo simulation for seismic analysis of a long span suspension bridge[J]. Engineering Structures, 2014(78): 100−111.

[3] 李建慧, 李爱群. 自锚式悬索桥静力随机分析与可靠度评估[J]. 中国公路学报, 2012, 25(6): 74−79. LI Jianhui, LI Aiqun. Stochastic analysis of static characteristics and reliability assessment for self-anchored suspension bridge[J]. China Journal of Highway and Transport, 2012, 25(6): 74−79.

[4] 骆勇鹏, 黄方林, 鲁四平, 等. 不确定性参数识别的模态区间逆响应面法[J]. 振动、测试与诊断, 2016, 36(5): 979−983. LUO Yongpeng, HUANG Fanglin, LU Siping, et al. Method for uncertain parameter identification using the modal interval inverse response surface[J]. Journal of Vibration, Measurement & Diagnosis, 2016, 36(5): 979− 983.

[5] 陈立宏, 陈祖煜, 刘金梅. 土体抗剪强度指标的概率分布类型研究[J]. 岩土力学, 2005, 26(1): 37−40. CHEN Lihong, CHEN Zuyu, LIU Jinmei. Probability distribution of soil strength[J]. Rock and Soil Mechanics, 2005, 26(1): 37−40.

[6] 唐小松, 李典庆, 周创兵, 等. 基于Bootstrap 方法的岩土体参数联合分布模型识别[J]. 岩土力学, 2015, 36(4): 913−922. TANG Xiaosong, LI Dianqing, ZHOU Chuangbing, et al. Bootstrap method for joint probability distribution identification of correlated geotechnical parameters [J]. Rock and Soil Mechanics, 2015, 36(4): 913－922.

[7] WAN Huaping, MAO Zhu, Todd M D, et al. Analytical uncertainty quantification for modal frequencies with structural parameter uncertainty using a Gaussian process metamodel[J]. Engineering Structures, 2014(75): 577− 589.

[8] Efron B, Tibshirani R. An introduction to bootstrap[M]. New York: Chapman & Hall Ltd, 1993.

[9] Hall P. Theoretical comparison of bootstrap confidence intervals[J]. The Annals of Statistics, 1988, 16(3): 927− 953.

[10] Akaike H. A new look at the statistical model identification[J]. IEEE Transactions on Automatic Control, 1974, 19(6): 716−723.

[11] Breiman L, Friedman J H. Estimating optimal transformations for multiple regression and correlation[J]. Journal of the American Statistical Association, 1985(80): 580−598.

(编辑 蒋学东)

The method for structure responses uncertainty analysis based on limited data

LUO Yongpeng1, HUANG Fanglin2, LIU Jingliang1, LU Siping2, XU Xutang1

(1. School of Transportation and Civil Engineering, Fujian Agriculture and Forestry University, Fuzhou 350108, China; 2. School of Civil Engineering, Central South University, Changsha 410075, China)

Measured data in practical engineering are often limited, which makes it difficult to determine the probability distribution of uncertain parameters. Therefore, the method for structure uncertainty analysis often assumes parameters to be random and obey a certain probability distribution. When the specified form of distribution assumptions does not accord with the actual, it may produce a large error. For this reason, a new method is proposed, which is suitable for structure dynamic responses uncertainty analysis based on limited data due to the case of the probability distribution is unknown. Firstly, the Bootstrap sample theory and Akaike Information Criterion (AIC) were adopted to determine the optimal probability distribution function and the distribution parameters based on the limited data, and then random sampling procedure was conduct, the random samples was generated into the response surface model to calculate the response, thus the influence of parameter variation to response can be rapidly quantify.With a numerical example to explore the influence of the original sample number and sampling frequency on analysis result, the recommendations of the original sample number and sampling frequency are presented. Finally, the feasibility and reliability of the proposed method were investigated by the numerical simulation of a cable-stayed bridge. The results show that the statistical uncertainty in probability distributions of uncertain parameters can be taken into account and optimal probability distribution function of parameter estimated accurately in the proposed method.

uncertainty analysis; limited data; sensitivity analysis; response surface model; Bootstrap sample

10.19713/j.cnki.43−1423/u.2018.12.026

TU318.1

A

1672 − 7029(2018)12 − 3217 − 08

2017−11−23

国家自然科学基金资助项目(51808122)；福建省中青年教师教育科研资助项目(JA170171)；福建农林大学高水平大学建设重点资助项目(113-612014018)；福建农林大学青年教师科研资助项目(113-61201401808)

骆勇鹏(1989−)，男，福建泉州人，讲师，博士，从事结构参数识别与损伤诊断研究；E−mail：yongpengluo@fafu.edu.cn