弹性支承块式无砟轨道钢轨纵向位移对比分析
金韶霞
(浙江科技学院 中德工程师学院,杭州 310023)
近年来无砟轨道技术发展迅速,由瑞士的Sonneville公司提出并开发的弹性支承块式无砟轨道是高速铁路应用最广泛的无砟轨道结构形式之一。它除了具有一般无砟轨道结构稳定性好、耐久性好、维修工作量少等优点外,还由于其较强的减振降噪特性,被大量应用于路基、桥上及隧道内部,在国内外地铁及隧道内均有成功铺设的经验[1-8]。弹性支承块式无砟轨道结构是在支承块下增设一块橡胶垫板(块下胶垫),并在支承块外包裹一层橡胶套靴,这与钢轨下的弹性垫板构成双层弹性体系,在最大程度上模拟了传统碎石道床弹性点支承的结构,弥补了无砟轨道弹性不足的缺点,并最大限度地实现了低振动低噪音[9-11]。但也正因其较高的弹性,容易导致轨道位移过大等问题,从而影响列车运行的平稳性与安全性[12]。与其他轨道结构相比,弹性支承块式无砟轨道还具有维修费用低、易于更换元件、建造成本低、轨道精度高、绝缘性好、空气动力性能好、轨道排水布置灵活等优势[13-14]。1966年瑞士铁路在隧道内首次试铺该型轨道结构,1993年开通运营的英吉利海峡隧道内也全部采用了此结构;中国自1995年开始进行弹性支承块式无砟轨道的研究,并先后在秦岭隧道及宁西线、兰武复线、宜万线、湘渝线等隧道内和城市轨道中进行了铺设[15]。随着弹性支承块式无砟轨道在实际工程中的广泛应用,对此结构的研究也越来越多[16]。钢轨作为弹性支承块式无砟轨道结构最重要的组成部件之一,其纵向位移,再对轨道研究而言意义重大。本研究基于德国慕尼黑工业大学测试机构对弹性支承块式无砟轨道结构中钢轨纵向位移的测试结果,将带有不同刚度的块下胶垫的弹性支承块式无砟轨道钢轨的纵向位移通过经典的Zimmermann法与有限元法分别进行计算,并对结果加以分析比较,从而验证了有限元模型计算的可靠性,为研究该类型的轨道结构提供参考。
1 计算方法
用经典的Zimmermann法与有限元法,对弹性支承块式无砟轨道的钢轨纵向位移进行计算与对比研究。经典的钢轨分析方法将钢轨假定为弹性点支承梁或连续弹性支承梁模型。点支承梁模型将扣件视为弹簧,钢轨按轨枕间距支承于轨枕之上;而连续支承梁模型则忽略轨枕间距,将下部基础对钢轨的作用看成均匀分布的弹簧连续支承着钢轨梁[17]。Zimmermann法是将钢轨假定为“由弹簧支承的无限长梁”,属于连续弹性支承梁模型[18]。用Zimmermann法计算钢轨纵向位移时先将轨枕支座转换成无限长梁的基数L[19]:
(1)
式(1)中:E为钢轨弹性模量;I为钢轨惯性矩;b为假定的无限长梁宽度;C为道床系数;a为轨枕间距;csy为结构总体刚度。
在计算钢轨纵向位移时考虑相邻轮轴的影响,引入相邻轮轴的影响系数ηi(i为相邻轮轴编号):
(2)
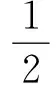
实际轨道结构中,扣件对钢轨既不是点支承,也不是连续支承,钢轨按轨枕间距固定在一定宽度的弹性垫板上,钢轨与弹性垫板的实际接触状态为面接触,因此钢轨下部的支承方式应该考虑为一定间距及一定宽度的均布支承。除了理论计算外,本研究还用德国的一个有限元结构设计软件Sofistik将弹性支承块式无砟轨道用有限元法进行建模与数值计算。建模时将结构构件进行有限元分析,而构件之间的连接则用弹簧进行模拟。
2 工程实例
2.1 Zimmermann法
选取的材料参数为:钢轨选取UIC60,轨枕间距为600 mm,荷载情况Ⅰ为集中荷载250 kN,荷载情况Ⅱ为UIC71。
根据Zimmermann方法进行计算的时候需要用到结构总体刚度,总体刚度由钢轨和混凝土支承块间的弹性垫板刚度、混凝土支承块与道床板间的块下胶垫与橡胶套靴的刚度计算而得。为了能够将此结构的计算结果与Sonneville产品技术规范里的值进行比较,块下胶垫刚度cpad分别取40、30、20、18 kN/mm,由此得出的结构总体刚度csy分别为31.1、24.7、17.5、15.9 kN/mm。
计算时引入集中荷载与UIC71 两种荷载情况。在集中荷载中给结构施加的是250 kN的轴重,而UIC71由4个间距为1.6 m的250 kN的轴重组成,单个轮载Qi为125 kN(此处不考虑集中荷载)。表1列出的是用Zimmermann法算得的钢轨在不同块下胶垫刚度cpad与集中荷载、UIC71 两种不同荷载情况下的纵向位移。

表1 钢轨纵向位移(Zimmermann法)Table 1 Vertical displacement of rail (Zimmermann method)
由表1可以看出,钢轨纵向位移与块下胶垫的刚度大小有着密切关联。块下胶垫的刚度越小,钢轨的纵向位移越大。钢轨在块下胶垫刚度为40 kN/mm及集中荷载与UIC71 两种荷载情况下的挠度曲线如图1~2所示。荷载情况集中荷载下的最大纵向位移出现在集中荷载下方,而荷载情况UIC71下的最大纵向位移则分别出现在中间2个荷载下方。
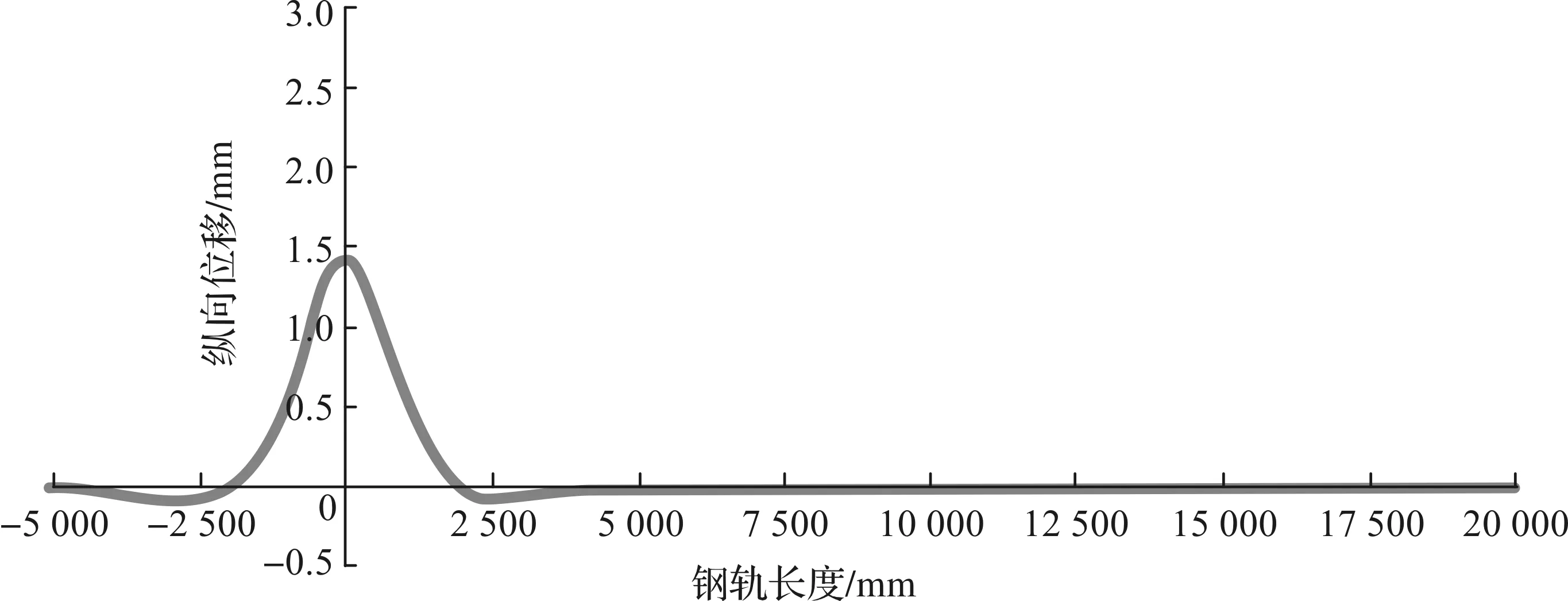
图1 钢轨在集中荷载作用下的挠度曲线Fig.1 Deflection curve of rail under concentrated load
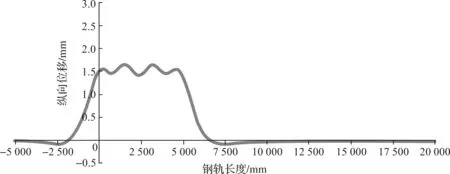
图2 钢轨在UIC71作用下的挠度曲线Fig.2 Deflection curve of rail at UIC71
2.2 有限元法
将钢轨与混凝土支承块定义为有限元,用Sofistik软件进行有限元实体模拟,计算条件不变。钢轨和混凝土支承块间的弹性垫片、混凝土支承块与道床板间的块下胶垫与橡胶套靴这些弹性部件均被模拟为竖向弹簧,而橡胶套靴四周则模拟成水平弹簧,此结构的三维空间模型如图3所示。弹簧系数的大小取决于弹性垫板、块下胶垫与橡胶套靴的刚度及弹簧数量。
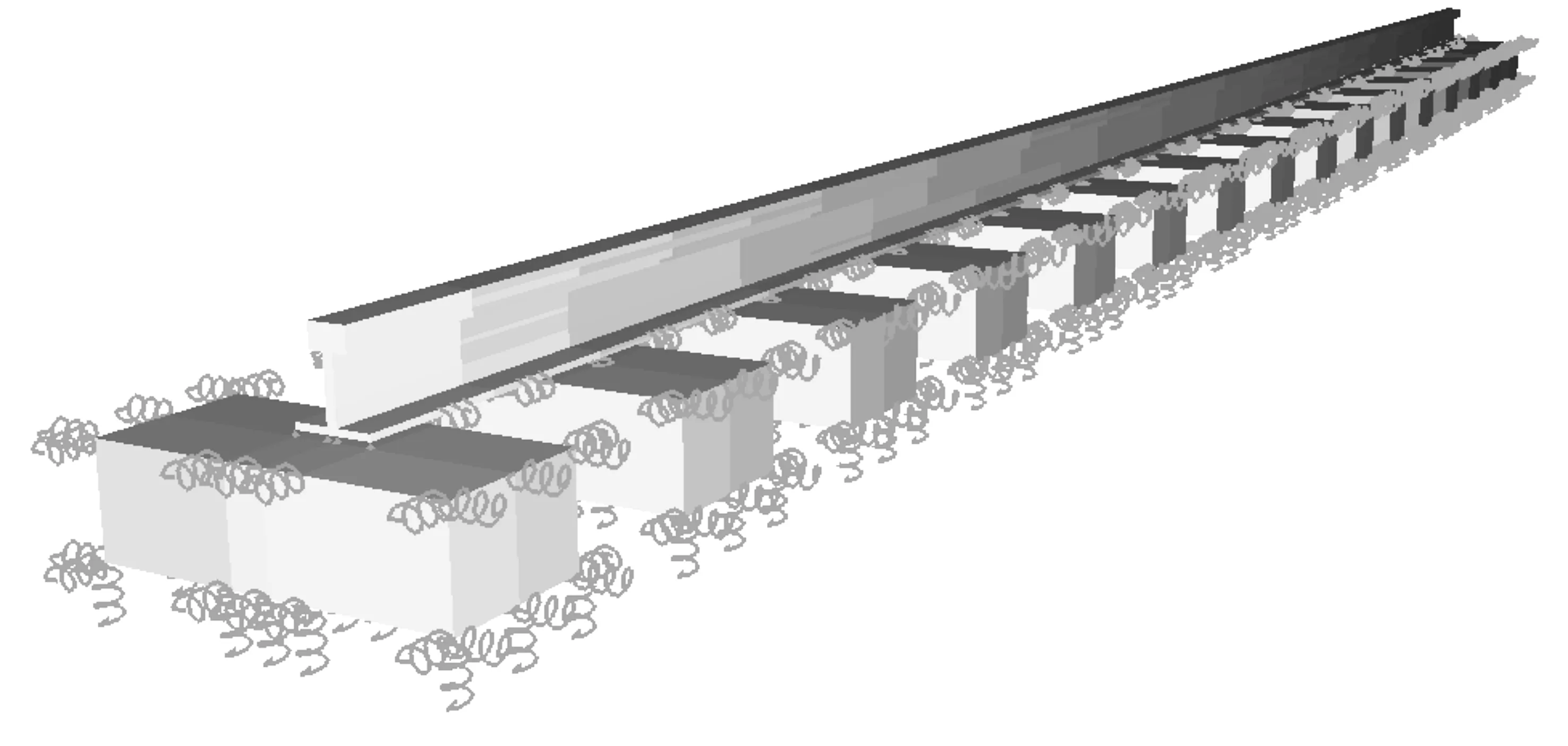
图3 用Sofistik对弹性支承块式无砟轨道进行有限元建模Fig.3 FE-Modeling of LVT with Sofistik
对弹性支承块式无砟轨道进行建模计算时同样也考虑集中荷载与UIC71 两种荷载情况。集中荷载下的最大纵向位移出现在荷载下方,见图4(荷载在跨中)和图5(荷载在支座上方)。

图4 荷载在跨中时集中荷载作用下的结构变形Fig.4 Suspended structure under concentrated load when load in the field
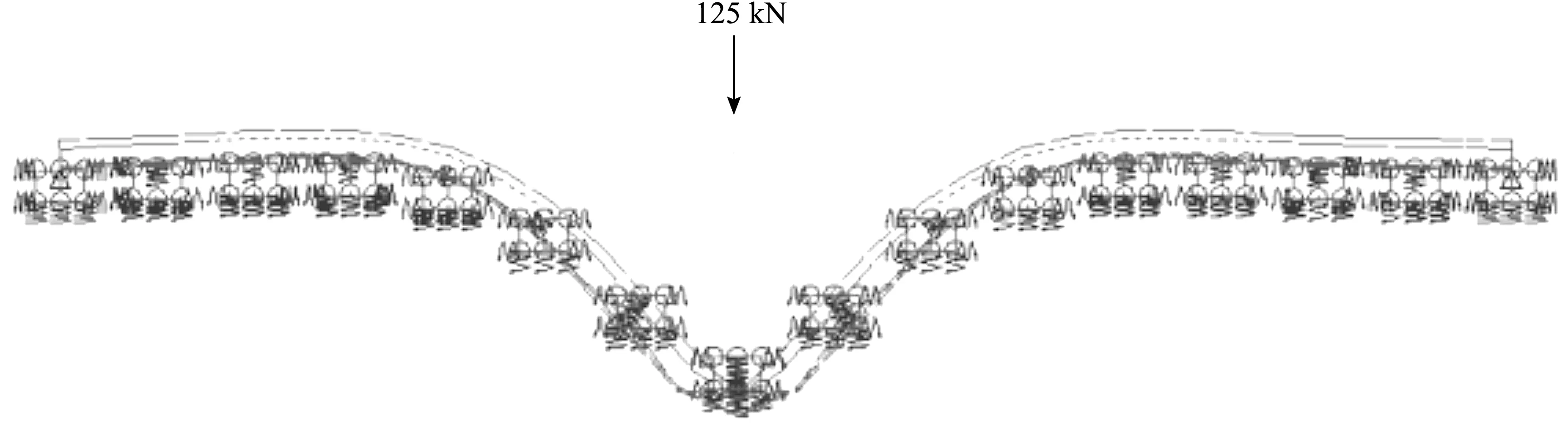
图5 荷载在支座上方时集中荷载作用下的结构变形Fig.5 Suspended structure under concentrated load when load over the bearing
在荷载情况UIC71下,选取一根长度为9 m的钢轨,分别对荷载Q1在离最左边支座2.1 m(跨中)和2.4 m(支座上方)的位置进行建模计算。此时最大纵向位移出现在中间两个荷载(Q2和Q3)下方,见图6(Q1离左边支座2.1 m)和图7(Q1离左边支座2.4 m)。
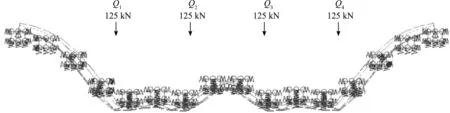
图6 xQ1=2.1 m时UIC71荷载情况下的结构变形Fig.6 Suspended structure at UIC71 when xQ1=2.1 m

图7 xQ1=2.4 m时UIC71荷载情况下的结构变形Fig.7 Suspended structure at UIC71 when xQ1=2.4 m
根据有限元法模拟得出的钢轨纵向位移见表2。

表2 钢轨纵向位移(有限元法)Table 2 Vertical displacement of rail (finite element method)
3 比较与分析
将表1和表2的数据进行比较,位移值在同一位置(跨中或支座上)没有明显区别,而且最大纵向位移的位置都随着荷载位置的改变而改变。根据有限元法得出的钢轨在块下胶垫刚度为40 kN/mm的集中荷载下的最大纵向位移是1.57 mm,而在UIC71荷载情况下的最大纵向位移是1.75 mm。钢轨在两种不同荷载情况下的变形曲线与Zimmermann法计算得出的弯曲线相似,集中荷载下的最大值出现在集中荷载下方(图1、图4和图5),UIC71荷载情况下的最大值出现在中间的2个荷载下方(图2、图6和图7)。
由Zimmermann法与有限元法计算得出的纵向位移差值介于0.04 mm和0.14 mm之间,其原因在于:
1)Zimmermann法是将钢轨假设成无限长梁通过弹性垫被固定于刚性底板的理论上,而根据有限元法得出的值基于实体模型;Zimmermann法里结构总体刚度由钢轨和混凝土支承块间的弹性垫板、混凝土支承块与道床板间的块下胶垫和橡胶套靴的刚度计算而得,而在有限元法里混凝土支承块与道床板间的刚度是由块下胶垫和橡胶套靴得出的。
2)采用有限元法对弹性支承块式无砟轨道进行模拟时,将钢轨与混凝土支承块之间的弹性垫层定义为弹簧,而在实际轨道结构中,钢轨与弹性垫板的实际接触状态为面接触,接触面尺寸为120 mm×160 mm,并非如弹簧是点支撑,接触面积也会影响钢轨的纵向位移值。
3)当荷载作用在跨中时,钢轨在被假定为连续梁考虑的情况下除了自身挠度外还会出现二次挠度。采用有限元法得出的钢轨纵向位移已经包括了二次挠度,而Zimmermann法在计算钢轨纵向位移时未考虑二次挠度的影响,因此值偏小。
4 结 论
用Zimmermann法与有限元法对弹性支承块式无砟轨道的钢轨纵向位移进行了计算与比较分析。两者计算结果相似,在相同荷载条件下同一位置的钢轨纵向位移没有明显区别,最大纵向位移的位置跟荷载位置有关,集中荷载下的最大值出现在集中荷载下方,而UIC71荷载情况下的最大值出现在中间的2个荷载下方。根据两种方法得出的位移值的偏差主要原因在于两者基于不同的模型、弹性垫板与钢轨之间的面接触以及钢轨的二次挠度。通过两种方法的比较,验证了有限元法计算该型结构的可靠性,但建模细节方面(如在建模时考虑弹簧系数)还有待进一步改善,使其更能体现实际结构。

