发动机散热器传热及内部流动试验研究

刘明月，沙 毅，王 宇

(浙江科技学院 机械与能源工程学院，杭州 310023)

机械的本质以动为主，这就需要配置电动机、发动机等原动机。田间移动作业的收割机、喷灌机等农业机械和部分缺乏电力的农副产品加工机械大多配置发动机为原动力。发动机一般都配置冷却系统，发动机在所有工况下运转时，水套中的冷却液保持在适当的温度范围(一般80～95 ℃)，温度过低或过高都对发动机工作不利。它主要由散热器、风扇、水泵和节温器等组成。散热器作为发动机冷却系统中最重要的部件之一，是在冷却系统处于大循环状态下，即水温超过节温器设置温度70 ℃后主阀门开启，冷却液流经散热器将所携带的热量散入大气以降低温度[1]。散热器根据芯子结构主要分为管带式和管片式，根据冷却管的平置和竖放分为横流式和纵流式。目前国内外大部分研究是针对管带式散热器的结构优化[2]、传热及阻力特性等进行的[3-8]，并且大多数都采用数值模拟方法进行研究，取得了一些成果，但专门针对管带式散热器内部传热及流动特性的研究相对较少[9-11]。本文以465Q型发动机管带纵流式散热器为研究对象，该机型是中国早期成功引进日本铃木发动机技术的典范之一，主要用于小型面包车、轿车和工具车等，其整车、发动机及冷却系统配置设计等均处于优等水平。要总结465Q型发动机冷却系统合理匹配的优越性，启发创新设计理念，为今后冷却系统智能化改造打下基础，实现降低油耗的目的，那就要首先进行试验研究，提供理论依据。本文就是在这样的背景下对核心部件散热器自然对流状况下传热性能及内部流动展开研究的，进而提出了散热器消耗功率比值和内部流动及散热规律，故具有一定的工程意义和参考价值。

1 管带式散热器结构与计算参数

1.1 465Q型发动机散热器结构

以465Q型发动机散热器作为研究对象，其主要参数见表1，几何模型正面如图1(a)所示，背面如图1(b)所示，散热管流道结构及主要尺寸如图1(c)所示，散热器主要组成及几何尺寸如图1(d)所示。散热器上下水室为Q235铁质材料，芯子为ZL102铝合金材料。散热管布置形式为双排平行布置，管形为扁管，散热管数量为68；散热带数量为35，厚度为0.08 mm。当节温器打开时，冷却液由进水口进入上水室，上水室的冷却液通过多根散热管流入下水室，最后由出水口流出。单根散热管过流面积A=34.069 mm2；散热器过流面积S=68A=0.002 316 7 m2。

表1 465Q型发动机及冷却系统主要参数Table 1 Main parameters of 456Q engine and cooling system

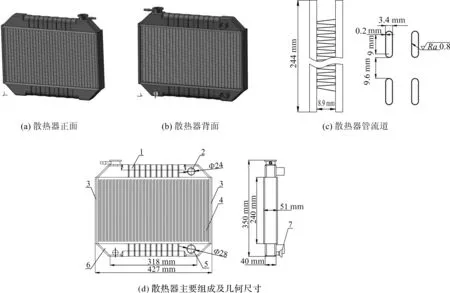
图1 散热器结构Fig.1 Radiator structure 1—上水室；2—进水口；3—侧护板；4—散热器芯；5—出水口；6—下水室；7—放水螺栓。

1.2 散热器计算参数

由于目前冷却液种类较多，其密度、动力黏度等物理参数难以查找或确定，故本文采用普通清水为研究介质，但两者物理性质存在一定的差别。散热器过流平均速度计算式[12]为：

(1)

式(1)中：qv为散热器体积流量；S为散热器内流道过流面积。

质量流量计算式为：

qm=ρqv。

(2)

式(2)中：ρ为水密度，随温度变化。

雷诺数计算式为：

(3)

式(3)中：dH为扁管当量直径；R为水力半径；x为过流断面A上被水湿润的固壁周线；μ为水的动力黏度，随温度变化；当Re≤2 320时，散热管中为层流；当Re>2 320时，散热管中为湍流。

散热器内部流动消耗功率计算式为：

P=qvΔp=qv(p1-p2)。

(4)

式(4)中：Δp为散热器进出口压强差。

散热器散热量计算式[13-14]为：

Q=CpqmΔt=Cpqm(t1-t2)。

(5)

式(5)中：Cp为水定压比热容；Δt散热器进出口水温差。

散热器消耗功率与散热量量纲相同，本文将其无因次比值定义为压热效率，计算式为：

2 散热器传热及流动特性试验

2.1 散热器试验台

散热器性能试验台结构如图2所示，试验台主要测量仪器精度见表2。试验时室温23 ℃，湿度56%，环境大气压1.011 6×105Pa[15]。

图2 散热器性能试验台结构Fig.2 Radiator test metering device

表2 主要测量仪器及精度 Table 2 Main measuring meters and precision

2.2 散热器自然对流性能试验方案

自然对流就是将所测散热器安装在室内试验台架上，外部无任何空气对流干扰，即在不涉及实际车载发动机行驶迎风和风扇强制空气对流情况下得出的结果。试验方案具体步骤为：1)设定调节4项散热器进水口流量qv分别为0.7、1.2、1.7、2.2 m3/h；2)每项流量qv下，再设定调节5项散热器进水口水温t1分别为70、75、80、85、90 ℃；3)每项工况下，分别读取散热器流量qv，进水口和出水口的温度t1、t2及压强p1、p2；4)分别计算散热器平均速度v、质量流量qm、雷诺数Re、压强差Δp、内部流动消耗功率P、温度差Δt、散热量Q和压热效率η等参数。

2.3 散热器传热及流动特性试验结果

表3为散热器性能测量与计算参数试验结果，图3(a)为散热器内部流动流量qv与压强差Δp和消耗功率P的变化规律；图3(b)为雷诺数Re与散热量Q的变化规律；图3(c)为雷诺数Re与压热效率η的变化规律。

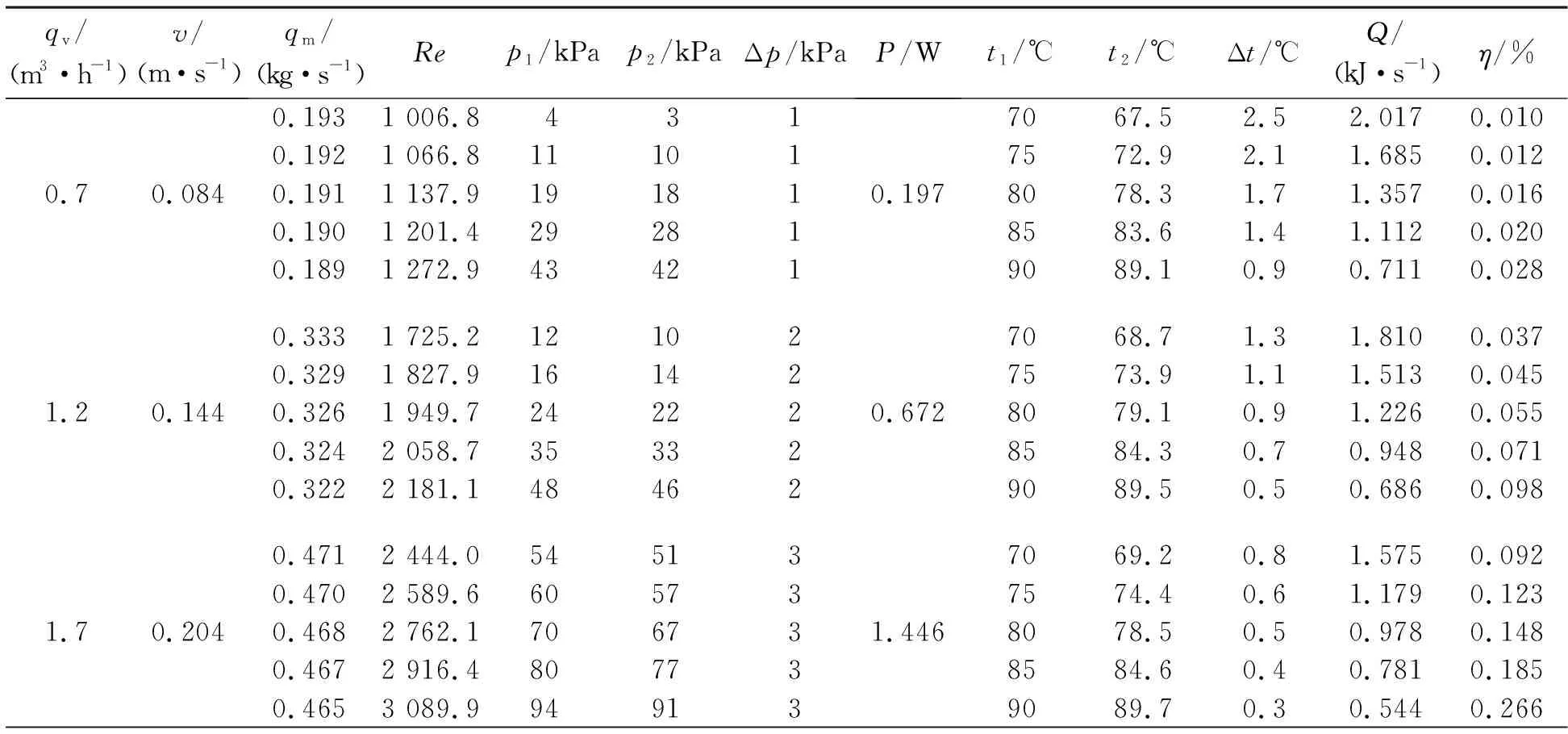
表3 散热器性能测量与计算参数(室温23 ℃)Table 3 Measured and calculated parameters of radiator performance(indoor temperature 23 ℃)

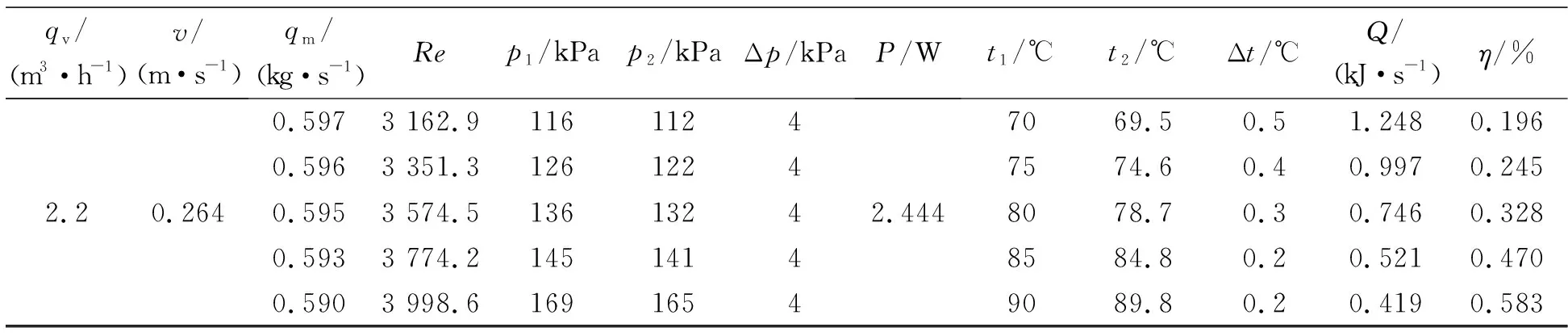
表3(续)

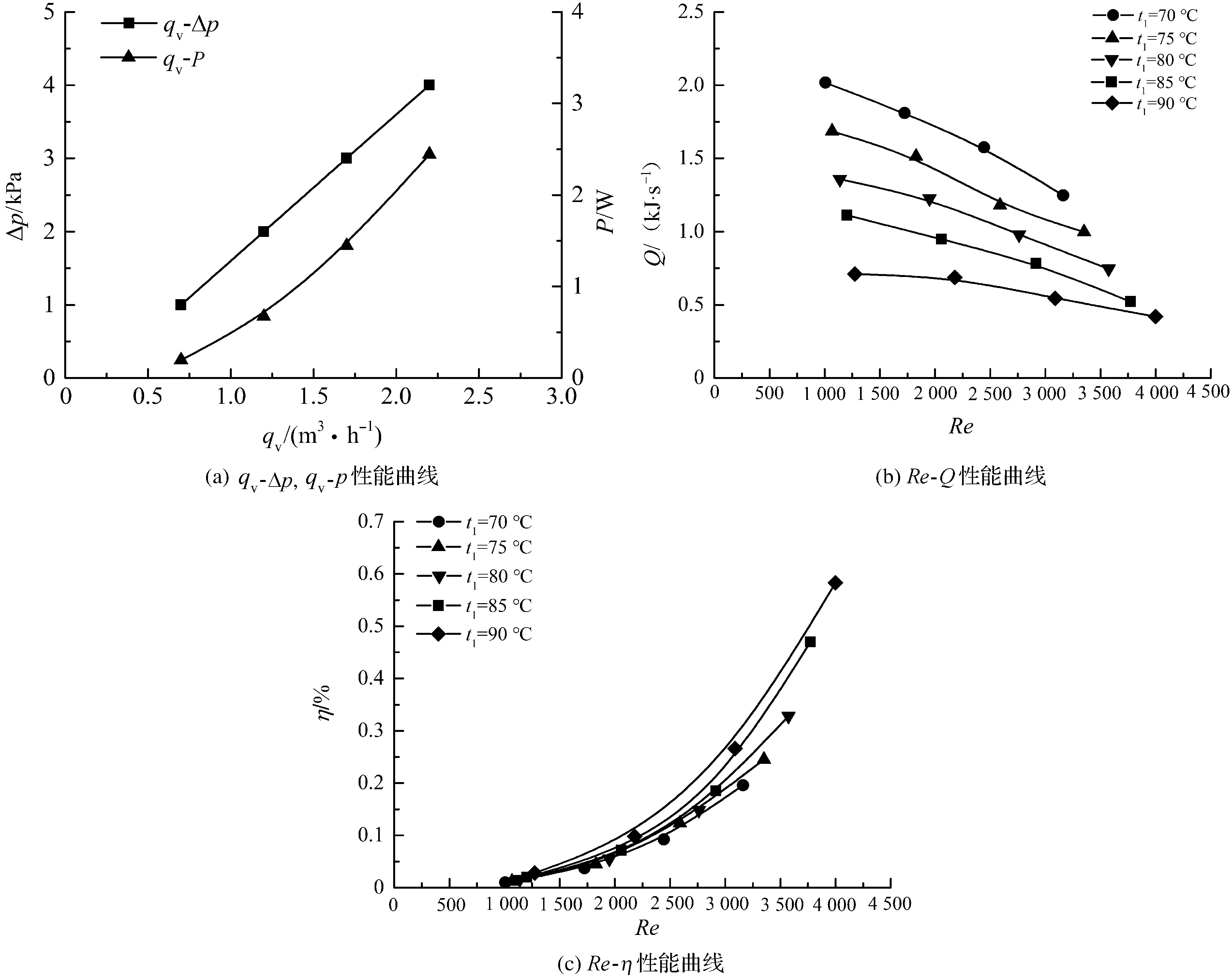
图3 散热器性能曲线Fig.3 Radiator performance curves

由表3和图3可以看出：1)通过散热器流量越大，进出口压强差愈大，流动损失功率亦愈大，呈近似直线规律递增。在等径管路中，由于流体与管壁及流体本身的内部摩擦，产生了沿程阻力。在管道中输送流体时常要克服沿程阻力而消耗功率。通过散热器流量增大，管道过流面积不变，流速会增大，根据牛顿内摩擦定律，切应力会随之增大，所以流动损失功率增加。2)进口温度越低，同雷诺数下散热量越大，进口温度相同，雷诺数越大散热量越小。3)进口温度越低，同雷诺数下压热效率越小，相对散热量越大，进口温度相同，雷诺数越大压热效率越大，相对散热量越小[16-17]。散热器结构成型，其外部与空气对流的散热面积是定值。理论上雷诺数越大，压热效率也越高，但散热器内部压差也越来越大，散热器内部流动消耗功率不断增大。因此，冷却液流量不能无限增大，压差损失功率不容忽视。

散热器进出口内径和面积分别为：di=0.024 m，do=0.028 m，Ai=0.000 452 4 m2，Ao=0.000 615 8 m2；表4为计算参数。由此可以看出，进出口水流雷诺数均已达到剧烈湍流的状态，这有利于水的混合搅拌。

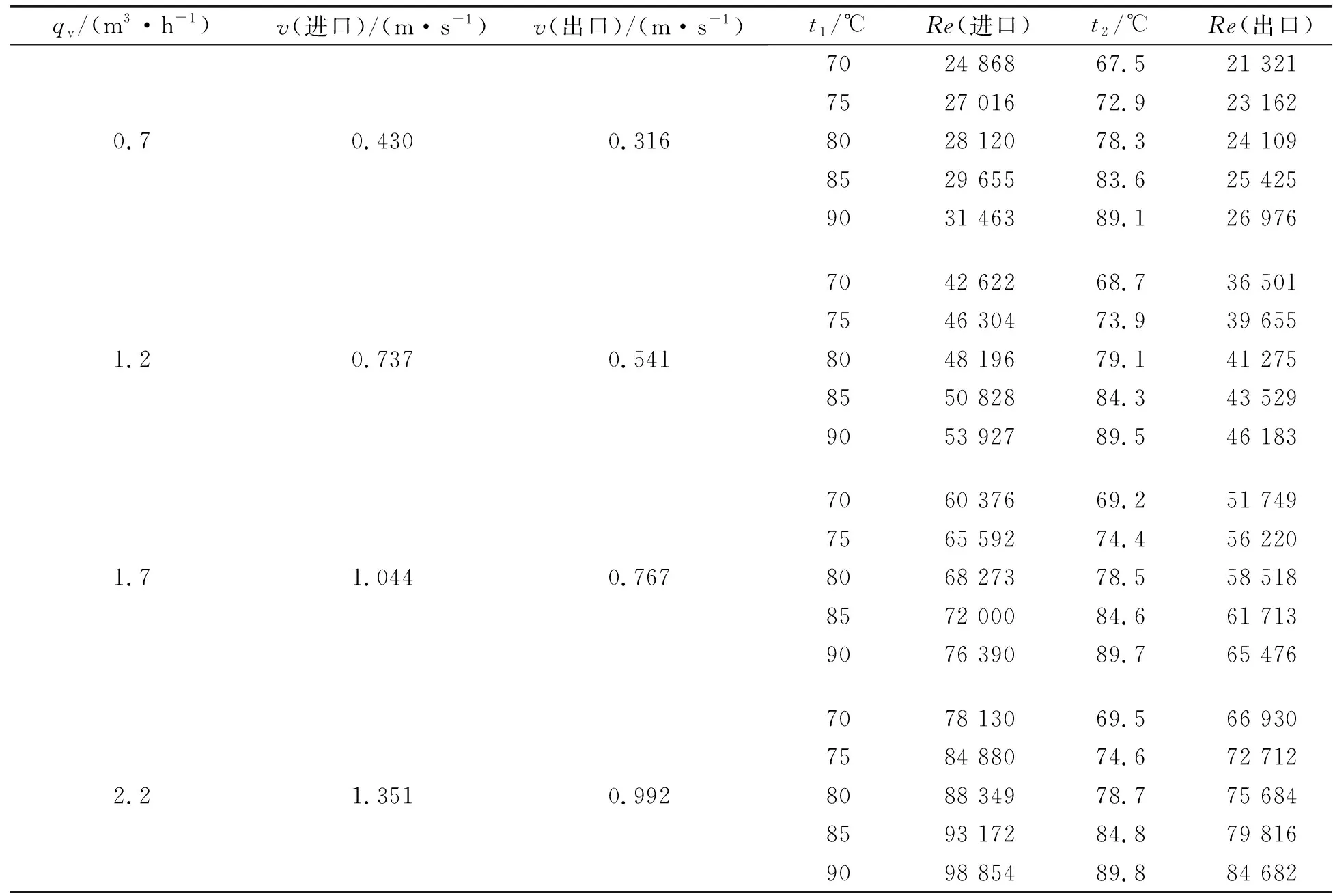
表4 散热器进出口计算参数Table 4 Calculated parameters of radiator inlet and outlet

3 散热器自然对流特性分析

3.1 散热器性能分析

由表3性能测量与计算参数经过数值分析可以拟合出散热器进出水口压强差Δp和内部流动损失功率P经验计算公式：

Δp=2qv-0.4，

(6)

(7)

式(6)～(7)中：qv为通过散热器体积流量，m3/h。

由式(6)～(7)可以看出，散热器进、出水口压强差Δp与流量呈直线性递增关系；流动损失功率P与流量呈抛物线性递增关系；当流量qv=0时，两者均应该为0，这是由数值分析经验公式拟合误差造成的。

拟合出散热量Q经验约束方程式：

Q=5.073 45-0.045 8t1-4.791 15×10-8Re。

(8)

式(8)中：散热器t1为进水口温度，℃；Re为散热器内部流动雷诺数。

由式(8)可以看出，散热器散热量Q与进水口温度t1和雷诺数Re均为直线性递减关系。同时拟合出散热器压热效率η经验计算公式：

η=3.151 91×10-8Re2+0.003 29t1-0.314 01。

(9)

由式(9)可以看出，压热效率η与进水口温度t1呈直线性递增关系，与雷诺数Re为抛物线性递增关系。

3.2 散热器性能误差分析

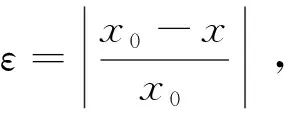
表5 散热器性能实测与计算数据对比及误差Table 5 Comparison and error of measured data and calculated data of radiator performance

对比分析可以发现本文拟合经验公式计算数据与实测数据相对误差最小是0，最大是0.748，说明两者误差较小，经验公式逼真度较大。

4 结 论

通过对管带纵流式散热器的传热特性及内部流动试验研究后得出以下结论：

1)管带纵流式散热器流量越小，雷诺数亦越小，同温下散热量越大，散热效果越好，层流散热效果好于湍流。同流量下，进水口温度越高，散热量越小散热效果越差。散热器内部流动不均匀，外部温度分布不均匀，散热量也不均匀。

2)正常运转下，散热器内部流动的最大消耗功率为2.444 W，发动机的额定功率为38.5 kW，经过计算得出，散热器内部流动的消耗功率只占发动机额定功率的0.006 5%，由于冷却液黏性大于水，其消耗功率会略大于水介质。

3)散热器的进水口和出水口均处于完全湍流流动状态。

4)单靠散热器自然对流换热一般难以达到发动机散热要求，故配置风扇加强散热是必要的。

本文经过大量的试验分别绘制出雷诺数和散热量、压热效率的关系曲线，并拟合出相关经验公式，可为今后该型及其他发动机冷却系统的智能化提供参考。