盲数和GM(1,1)模型在性能退化产品可靠性分析中的应用
盖炳良,滕克难,王浩伟,陈 瑜,孙 媛
(海军航空大学,山东 烟台 264001)
0 引言
如何表达和处理不确定信息是可靠性工程面临的不可避免的挑战[1],而性能退化过程可视为一个部分已知、部分未知的灰色系统,因而灰色系统理论可应用于性能退化可靠性分析,且GM(1,1)对小样本建模的有效性[2]使之可有效解决小样本、贫信息的建模困难。因而本文将盲数和GM(1,1)等灰色理论方法引入性能退化可靠性分析中。
盲数实质是建立区间灰数和可信度。不考虑概率分布时,常采用自然断点法构建区间灰数,用判断矩阵法[3]或直接用数量百分比建立可信度,这类方法的局限在于盲数的建立完全受限于现有数据。考虑概率分布时,文献[4]考虑故障率服从浴盆曲线,将区间总长度设为故障率最大值与最小值的差值,再等分确定各区间灰数,可信度设为区间故障率对应时间与寿命周期的比值;文献[5]假设退化量服从正态分布,由“3σ”性质确定区间灰数和可信度。
三参数威布尔分布应用范围广泛,其参数估计方法较多:文献[6]以秩回归方法获取初始值,采用非线性最小二乘法得到参数估计值;文献[7]也以秩回归方法获取初始值,并用神经网络和遗传算法优化;也有采用灰色模型方法进行参数估计的,GM(1,1)建模条件的优点是小样本建模,通常只需4~10个样本[8];文献[9]采用GM(1,1)直接建模方法对三参数威布尔分布进行参数估计,认为若形状参数大于1,则拟合度好,精度较高,但没有考虑GM(1,1)建模中原始序列和累加序列的区别,且没有考虑初始条件的优化和参数估计值的进一步优化等。
因此,本文通过模型选择择优确定概率分布,并用灰数排序方法优化可信度;假定各测量时刻点的可靠度值,在服从三参数威布尔分布条件下,采用GM(1,1)建模方法估计和优化参数。
1 基于盲数的测量时刻点可靠度
按照盲数定义[4]构建退化数据盲数和失效阈值盲数。
1.1 退化数据盲数
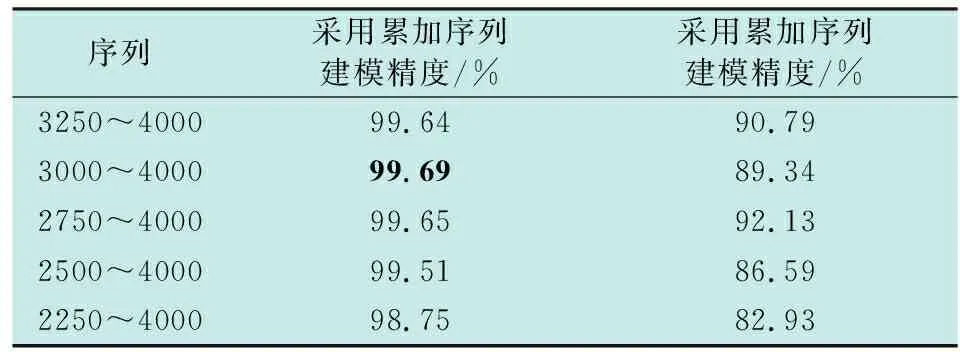
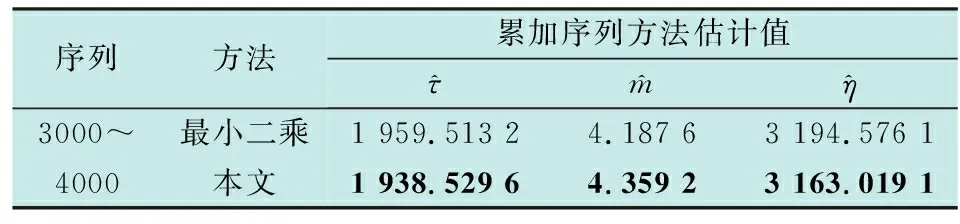
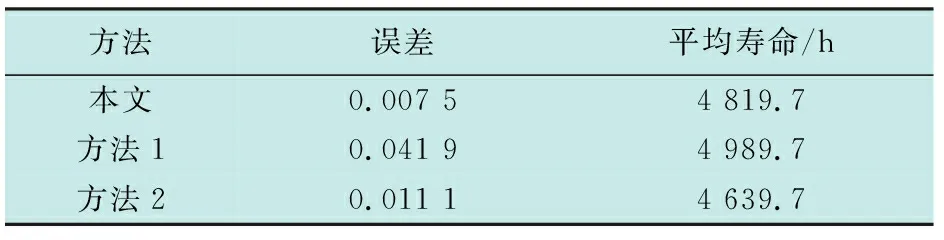
假定产品性能退化服从单调递增(单调递减同样适用),性能退化试验采用平衡测量,即不同样品的测量数据是在多个时刻同时测量得到。设tk为第k次测量时刻,记测量时刻为t1 以Xk为tk时刻的性能退化数据,X·k表示tk时刻退化数据区间灰数,αj为Xk在区间灰数X·k中的可信度,α为总可信度,X·k∈g(I),nx为盲数阶数,则tk时刻的性能退化数据的盲数定义为 (1) 设L为失效阈值,Lo为失效阈值区间灰数,βj为L在区间灰数Lo的可信度,β为总可信度,Lo∈g(I),nl为盲数阶数,因而,失效阈值盲数定义为 (2) 若在tk时刻产品退化量Xk超过产品阈值l,则称为产品失效,产品在tk时刻的可靠度为 R(tk)=P(Xk (3) 由式(1)~式(3)得盲数可靠度算式为 R(tk)=P(Xtk (4) R(tk)=P(φ(γ)>0)。 (5) 盲数运算时,可能出现区间交叉,设li=[ldn,lup]∈Lo,Xi=[xdn,xup]∈X·k,当出现式(6)中任意一种情形时,就认为出现区间交叉,即 (6) li-Xi>0,表示lup-xdn>ldn-xup≥0;li-Xi=0,表示lup-xdn≥0>ldn-xup,则 (7) 可见处理区间交叉时式(7)折合了区间中大于0的可信度,折合系数λ按均匀分布来计算,若考虑概率分布,则不宜按均匀分布来计算[10]。 假设退化量和失效阈值相互独立。图1中显见xdn 图1 灰数排序Fig.1 Interval grey number ranking 当xdn (8) 当ldn (9) 当xdn (10) 当ldn (11) 经盲数运算,求得测量时刻可靠度值,形成一个离散可靠度序列{tk,R(tk)},k=1,2,…,M。假设产品寿命服从三参数威布尔分布,即 (12) 式中,τ,m,η分别是位置参数、形状参数和尺度参数。式(12)经变换可表示为 (13) 令Rk=ln[-lnR(tk)],则(Rk,tk)满足 (14) 下面基于非等间距GM(1,1)模型对τ,m,η进行参数估计。 由微分方程解的性质可得 (15) (16) 则由定义可得,原始序列模拟值为x(0)(tk)=(x(1)(tk)-x(1)(tk-1))/Δtk={cexp(-atk)[1-exp(aΔtk)]}/Δtk,k=2,3,…,M。 比较式(14)和式(16),易得 (17) 取在80℃条件下某GaAs激光器工作电流随时间变化的百分比数据,详细数据可见文献[12],试验样本个数为15,每250 h测试一次,至4000 h为止,阈值为10。 参考已有文献对同一批数据分析时假定过的分布模型,选择正态分布、威布尔分布、Gamma分布和对数正态分布4种分布作为待选模型,对各测量时刻的退化量分布进行AD检验。 图2 tk=3500 h时的性能退化模型选择Fig.2 Degradation model selection when tk=3500 h 图2所示为当tk=3500 h时的检验结果,可见当tk=3500 h时对数正态分布AD值最小,是最优分布。 表1给出了未修正折合系数λ时各测量时刻的可靠度,同时对比了修正后的结果,其中250~1750 h的可靠度为1。 表1 各测量时刻基于盲数的可靠度 (α=1,β=1) (18) 表2 建模精度比较 表3 三参数威布尔分布参数估计值 考虑其他2种方法。方法1:由盲数方法求得测量时刻点可靠度,再按极值分布进行参数估计,获取可靠度函数。方法2:即文献[12]方法,认为每个测量时刻点退化量服从正态分布,并采用极值分布估计参数。 表4是3种方法的比较,可见,本文方法拟合精度最高,平均寿命为4 819.7 h。 表4 3种方法结果分析比较 图3所示是3种方法所得的可靠度曲线图,本文方法得到的可靠度曲线介于方法1和方法2得到的可靠度曲线之间。 图3 可靠度曲线Fig.3 Reliability curves 本文主要研究盲数和GM(1,1)建模等灰色系统方法在性能退化产品可靠性分析中的应用。首先采用模型选择,运用盲数理论求得各测量时刻的可靠度,然后采用GM(1,1)建模方法对三参数威布尔分布进行参数估计,求得可靠度函数。通过3种方法在GaAs激光器退化数据上的应用比较,验证了本文方法的合理有效性。主要结论如下: 1) 采用灰数排序方法修正灰数区间交叉时的可信度值,避免均匀分布造成的误差; 2) 基于GM(1,1)的三参数威布尔分布参数估计方法,避免了反复迭代,简单明了,且相比于极值分布近似方法具有更好的拟合精度; 3) 下一步如何将灰色系统方法应用于多元退化、退化与突发竞争失效等性能退化过程,有待进一步深入研究。1.2 失效阈值盲数
1.3 tk时刻可靠度
P(h(L)-f(Xk)>0)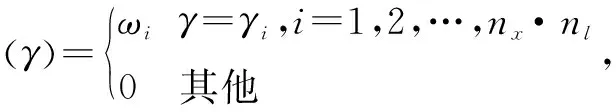

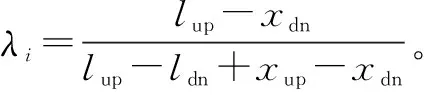


2 产品可靠度
2.1 非等间距GM(1,1) 参数估计
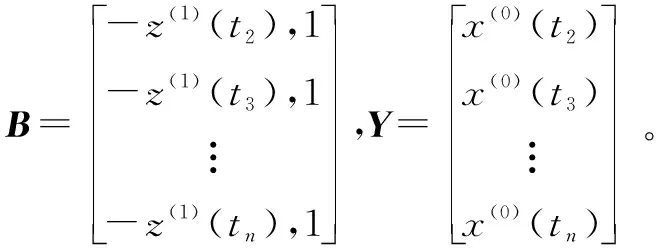

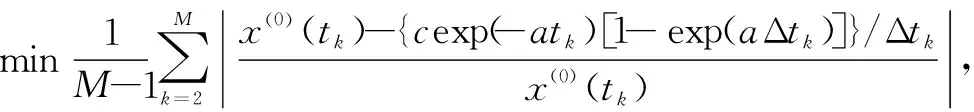
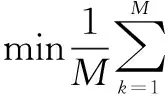
2.2 三参数威布尔分布参数估计

3 实例
3.1 择优选择tk时刻的退化量分布

3.2 tk时刻的产品可靠度


3.3 产品可靠度
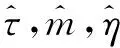
4 进一步讨论

5 结束语

