无人机协同作战兰彻斯特方程设计与作战进程预测

黄吉传，周德云

(西北工业大学电子信息学院，西安 710072)

0 引言

随着未来作战模式逐渐向协同化转变，无人机协同作战相关技术成为目前的研究热点。无人机协同作战效能评估技术能够对无人机协同执行任务的好坏程度进行分析与评价，从而得到无人机在不同载荷和不同型号协同下的任务执行效能[1-2]，以便对无人机任务进行调整。但是无人机协同效能评估技术通常只能给出当前配置下的无人机协同作战效能值，仅能够为指挥决策人员提供作战前的参考，不能与实际作战相结合，缺乏由评估到作战的一体化联系。兰彻斯特(Lanchester)方程[3]能够描述敌我双方兵力变化，是作战进程预测的经典方法之一。因此为了实现由评估到作战的一体化集成，为指挥决策人员提供更全面的决策信息，研究无人机协同作战兰彻斯特方程的设计与无人机协同作战进程预测方法具有重要的意义。

目前对于兰彻斯特方程的研究多集中于理论分析[4-6]，随着协同作战逐渐成为主要的作战模式，研究人员已开始关注协同作战兰彻斯特方程的设计问题。文献[7]针对体系对抗效能评估问题，建立了多元兰彻斯特方程，实现了体系对抗双方的效能评估；文献[8]引入协同系数概念和相关性指标，建立了协同作战兰彻斯特方程；文献[9]分析了协同作战的基本要素，引入协同影响因子，建立了协同作战兵力损耗兰彻斯特方程；文献[10]量化了协同作战中各作战单位间的协同影响，建立了合同作战兰彻斯特方程；文献[11]考虑了数据链对飞机作战性能的影响，建立了改进的兰彻斯特方程，并实现了航空作战进程预测，有效地解决了由评估到作战的一体化集成问题。但是以上文献所提出的兰彻斯特方程均没有对无人机协同作战的特点进行研究和设计，并不能直接应用于无人机协同作战的进程预测分析。

针对以上问题，本文重点研究无人机协同作战兰彻斯特方程的设计问题，在传统协同作战兰彻斯特方程的基础上，考虑无人机协同作战对地攻击任务，设计了无人机协同作战兰彻斯特方程。在此基础上，基于增援和载荷变化对无人机协同作战兰彻斯特方程进行了扩展，设计了基于增援的无人机协同作战兰彻斯特方程以及不同载荷下的无人机协同作战兰彻斯特方程。仿真实验采用本文所设计的无人机协同作战兰彻斯特方程对作战双方兵力损耗过程进行了分析，同时基于所提出的扩展无人机协同作战兰彻斯特方程，分别分析了载荷变化以及战斗增援对作战进程的影响。仿真实验证明了所设计的无人机协同作战兰彻斯特方程的合理性和可行性，有效实现了由评估到作战的一体化集成。

1 协同作战兰彻斯特方程概述

英国汽车工程师兰彻斯特于1914年提出的战斗损耗理论，采用一组微分方程描述了交战双方人员损耗规律，这组方程即兰彻斯特方程[3]，该方程能够在给定的假设下给出交战双方人员损耗随时间的变化规律。

传统兰彻斯特方程只考虑单一兵种，并不适用于多种不同型号无人机协同作战。随着越来越多的研究人员关注无人机协同作战问题，提出了一些改进的协同作战兰彻斯特方程，但其本质上还是基于基本协同作战兰彻斯特方程所建立的。因此，本文首先给出协同作战情形下的基本兰彻斯特方程。

假设作战的红蓝双方目标分配已确定，红蓝双方分别有m和n种作战单元，则红方兵力可表示为X={x1，…，xi，…，xm}(i=1，2，…，m)，蓝方兵力可表示为Y={y1，…，yj，…，yn}(j=1，2，…，n)，其中，xi为红方第i种作战单元的兵力数量，yj为蓝方第j种作战单元的兵力数量，则协同作战兰彻斯特方程[10]可表示为

(1)

式中：αij是xi对yj的损耗率系数；βij是yj对xi的损耗率系数；φij是xi攻击yj的概率；ψij是yj攻击xi的概率，i=1,2,…,m，j=1,2,…,n。

若考虑战斗增援和非战斗减员，则协同作战兰彻斯特方程可表示为

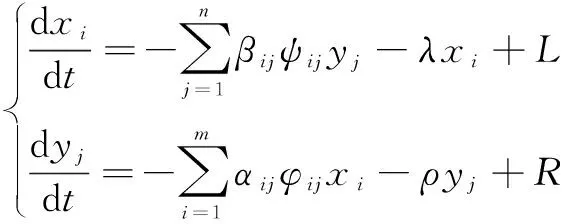
(2)

式中：λ和ρ分别为红蓝双方非战斗损失率；L和R分别为红蓝双方兵力增援速度。

2 无人机协同作战兰彻斯特方程设计与扩展

2.1 无人机协同作战兰彻斯特方程设计

无人机协同作战兰彻斯特方程设计需要考虑无人机协同作战的具体任务需求以及任务背景。考虑以下无人机协同作战场景：多种型号察打一体无人机协同作战进行对地打击，其攻击目标为敌方重要军事设施。这些需要打击的军事设施均比较隐蔽，只能通过情报预知其大致方位，由无人机侦察确认目标后才能进行打击。同时每个需要打击的军事设施周围都有防空系统，可对我方无人机进行精确打击。由于双方兵力较分散，均无法集中火力打击对方某个目标，因此其符合兰彻斯特方程第二线性律。根据该作战场景可给出如下2个假设。

1) 无人机分散侦察。当一架无人机到达任务区域后经过数据链通知其他无人机，其他无人机才会相继到达该任务区，因此无人机到达敌方领空的架次x=x(t)是服从参数为λ的泊松分布的随机变量。当无人机侦察到敌方设施后，可对相应设施进行精确制导打击，且毁伤概率正比于无人机协同作战的能力。无人机侦察发现并锁定敌方目标的时间间隔是服从参数为μ的指数分布的随机变量。

2) 敌方防空系统为精确制导导弹，其雷达对无人机的发现时间间隔是服从参数为η的指数分布的随机变量，其一次攻击的时间间隔也是服从指数分布的随机变量。假设当指定敌方目标设施被摧毁时，其周围的防空系统也被看作已摧毁，每个敌方目标周围的防空系统火力单元配置均一致，因此可将一个敌方目标设施与其周围的防空系统看作一个敌方作战单元，其作战单元数量用y=y(t)来表示。

根据以上假设可建立无人机协同作战兰彻斯特方程。由假设1)可知，无人机协同侦察设备在时间τ内未发现敌方目标的概率为px 0(τ)=e-μτ，则在时间τ内发现任何目标的概率为px1(τ)=1-e-μτy(t)。因此，一架无人机发现并摧毁敌方一个目标的概率为

px=P(1-e-μτy(t))

(3)

式中，P为无人机对目标的杀伤概率。

由于无人机对目标的毁伤概率正比于无人机协同作战的能力，因此假设无人机协同作战能力为α，则P=kα，k为比例系数。如果将无人机协同作战能力α归一化到[0，1]内，则有P≈α。因此，一架无人机发现并摧毁敌方一个目标的概率可表示为

px=α(1-e-μτy(t))。

(4)

在时间τ内x=X(t)个无人机协同摧毁敌方目标的数学期望为

E(y)=X(t)α(1-e-μτy(t))

(5)

敌方作战单元数量的损耗率可表示为

(6)

由假设2)可知，敌方防空系统在时间τ内未发现我方无人机的概率为py 0(τ)=e-ητ，则在时间τ内发现任何目标的概率为py1(τ)=1-e-ητx(t)。因此，一个敌方作战单元发现并摧毁我方一架无人机的概率为

py=P*(1-e-ητx(t))

(7)

式中，P*为敌方作战单元对我方无人机的杀伤概率。

考虑到敌方作战单元对不同类型无人机有不同的杀伤概率，所以在时间τ内，y(t)个作战单元毁伤无人机的数学期望为

(8)

因此，无人机的损耗率可表示为

(9)

此外，考虑到无人机的协同作战能力随着无人机数量的减少而减弱，因此无人机的协同作战能力随着作战进程的推进而减弱。设协同能力的变化由协同影响因子ε表示，则无人机协同作战兰彻斯特方程可表示为

(10)

2.2 考虑兵力增援下无人机协同兰彻斯特方程扩展

在实际作战中，战场态势是动态变化的，我方决策人员可以根据当前任务需要，派遣无人机对当前作战进行支援。因此为了研究不同增援情况对作战进程的影响，需要设计增援情况下的无人机协同作战兰彻斯特方程。

根据式(10)，考虑增援情况，同时不考虑非战斗减员，无人机协同作战兰彻斯特方程可扩展为

(11)

式中，L和R分别为双方兵力增援速度。

2.3 不同载荷下无人机协同作战兰彻斯特方程扩展

无人机协同作战兰彻斯特方程能够描述无人机协同作战中双方兵力的变化情况。在实际作战中，无人机会根据任务需求而携带不同类型的载荷，例如装载小功率的雷达同时装载更多武器，或者装载大功率雷达和电子侦察设备同时装载较少武器。这样，不同任务载荷的无人机协同作战，对作战任务的完成必然会有不同的作战效能。通常来说这种影响不仅体现在作战能力的增加，同时还使得我方作战形势更有利，从侧面对敌方产生了压制效果。因此需要对无人机协同作战兰彻斯特方程进行扩展，以便更好地分析携带不同载荷对无人机作战产生的影响。

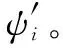
(12)

由于无人机性能改变使作战能力得到提升，所以在敌方能力未变化的情况下，其能力的提升将使我方具备更大的优势，从而对敌方产生适当的压制作用。因此提出采用能力占优因子描述该能力的变化对双方带来的影响。能力占优因子可以表示为

σ=δ-ξ

(13)

式中，ξ为无人机载荷变化给敌方带来的毁伤能力的改变。

根据以上分析，载荷变化下无人机协同作战兰彻斯特方程的扩展可表示为

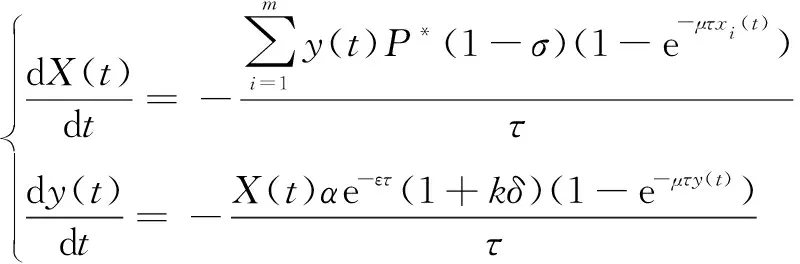
(14)

式中，k为战斗变化率系数。

3 仿真实验

3.1 作战双方兵力损耗过程分析

假设我方有A和B两种类型的无人机，我方根据实际作战任务分配多架无人机协同执行对地打击任务，敌方有5个目标，其对我方A型无人机的毁伤概率为0.6，对我方B型无人机的毁伤概率为0.7，无人机协同作战能力可由效能评估计算得到，也可由专家经验给出。为了便于分析，在此仅给出不同数量无人机协同作战效能值，不讨论详细计算方法。不同数量无人机协同作战能力值见表1。

表1 不同数量无人机协同作战能力值

根据专家经验知识有μ=η=2，协同影响因子ε=0.05，无人机的作战能力α分别取2.0，1.8，1.6，1.4，1.2，1.0和0.8，得到双方兵力变化对比，如图1所示。

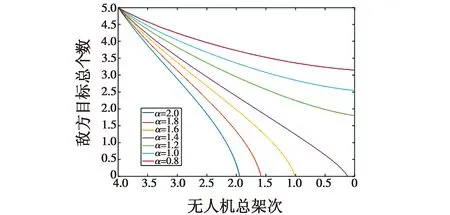
图1 双方剩余兵力变化对比图Fig.1 Residual force change of the two sides

从图1可见，当我方作战效能约大于1.4时，我方在消灭全部敌方目标后能够保证我方有兵力剩余。但是考虑到我方无人机的数量是整数，因此必须使得我方作战效能大于1.6才能保证我方在实际作战中获胜。因此，当使用4架无人机协同时，至少要使作战效能达到1.6。但是以目前我方无人机的配置，要使4架无人机协同总效能满足要求，需要挂载更强的雷达或者更强的武器，使协同作战效能至少增加0.3。由于效能要增加0.3，需要大大改进无人机的性能，以当前装备能力来看是很难达到的，因此需要采用5架无人机进行协同作战，这样才能够保证我方战斗胜利。假设采用5架无人机协同作战，其作战效能为1.92，可得到双方剩余兵力变化如图2所示。

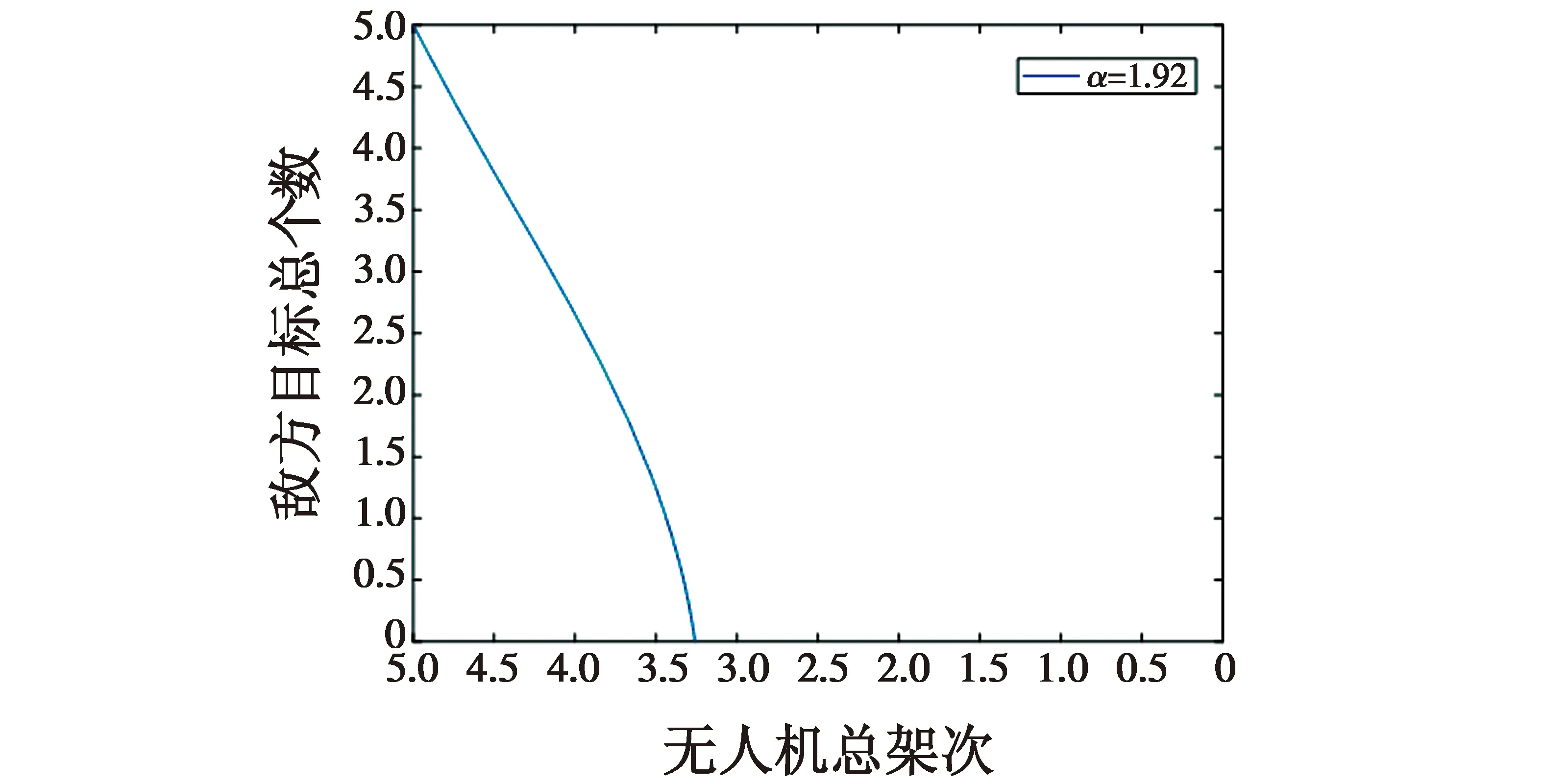
图2 5架无人机协同下的双方兵力变化图Fig.2 Force change of the two sides under the coordination of five UAVs

由图2可见，当采用5架无人机协同作战时，在消灭全部敌人后还剩余3架无人机，这种配置大大提高了我方的作战成功率，同时还能够降低我方无人机的损耗。

根据以上分析可知，本文所设计的无人机协同作战兰彻斯特方程能够有效描述无人机协同作战时的兵力变化，帮助指挥决策人员改进或做出正确的无人机配置方案，有效地将无人机的效能与实际作战相结合，实现了无人机协同作战效能评估和实际作战应用的一体化集成。

3.2 载荷变化对作战进程的影响分析

假设我方A型无人机现有两种配置方案可供选择：一种携带全面的电子对抗设备，同时限于载荷要求，只携带4枚对地导弹；另一种配置中，A型无人机仅配备雷达告警系统，未携带相关电子对抗设备，但是挂载8枚对地导弹。假设我方使用2架A型无人机和2架B型无人机协同作战，根据专家经验知识和效能计算，其在两种配置下的协同作战能力分别为1.61和1.68。但是，由于第一种配置中无人机携带了全面的电子对抗设备，对敌方起到显著的压制作用，因此根据专家经验知识可设占优因子σ=0.2，战斗变化率系数k=5。经过计算可得两种配置下双方兵力的动态变化曲线，如图3所示。

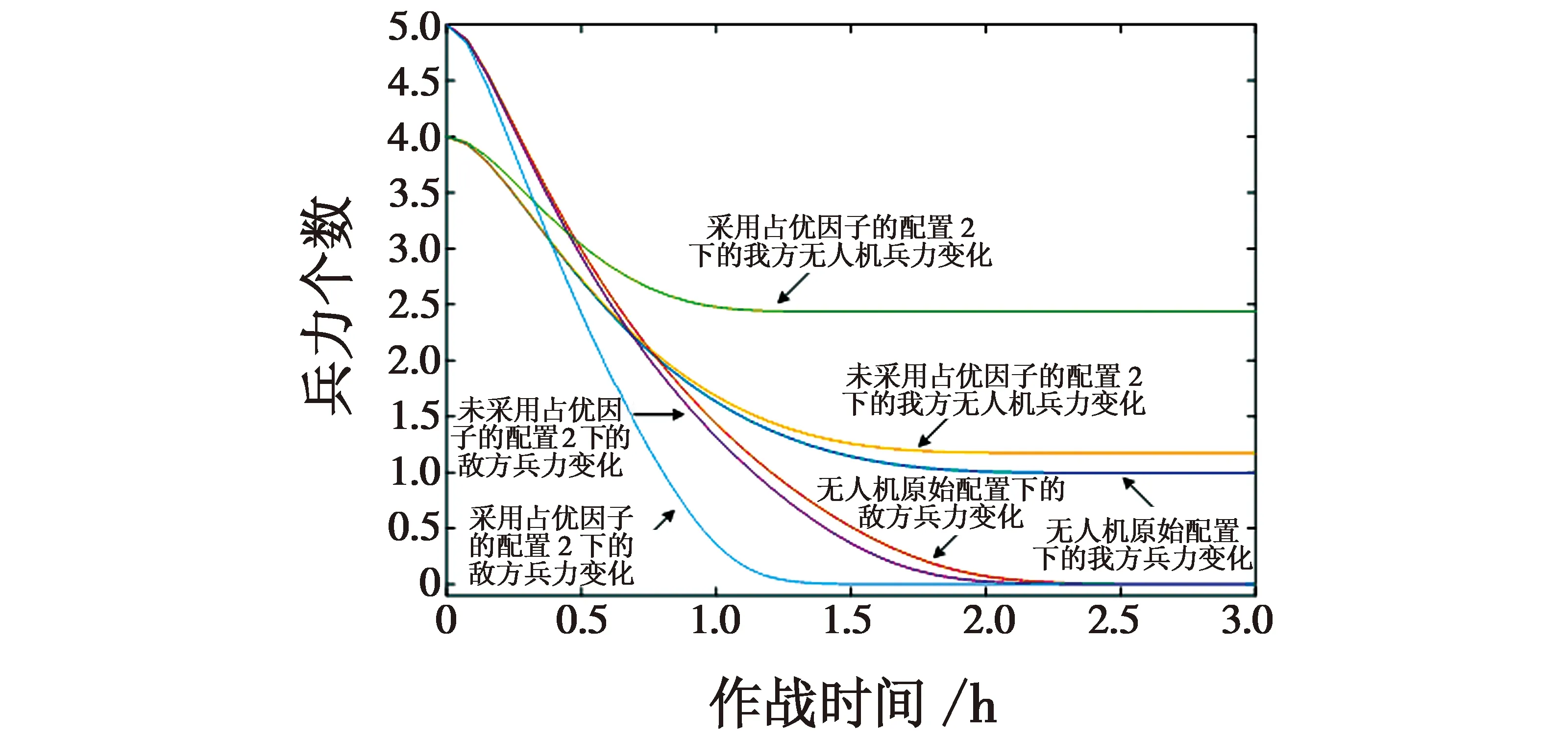
图3 载荷变化下的双方兵力动态变化曲线Fig.3 Dynamic change of forces of two sides under payload change

由图3可见，在原始配置下我方在完全消灭敌方后，还能够剩余1架无人机；在改变无人机载荷后，如果不考虑占优因子，则我方无人机同样剩余1架。根据实际作战，我方加入了大量的电子对抗设备，通过电子对抗设备能够实现多种电子干扰和抗干扰手段，这将显著影响整体作战进程。但是如果不考虑载荷的占优因子，只根据当前性能进行分析，那么增加全面的电子对抗设备对我方作战并不能起到明显作用。此外，由图4可见，当加入占优因子后，我方在完全消灭敌方后还能够剩余2架无人机，充分体现了载荷变化对作战的影响。

因此根据以上分析可见，本文所提出的不同载荷下无人机协同作战兰彻斯特方程能够有效反映载荷变化对作战进程的影响，为实际作战中不同装备配置方案提供合理的参考依据，是指挥决策人员分析无人机协同作战进程必不可少的理论支撑。

3.3 战斗增援对作战进程的影响分析

战斗增援决定了战斗胜负的走向，基于本文所设计的考虑增援条件下的无人机协同作战兰彻斯特方程，主要讨论增援对无人机协同作战的影响。假设我方初始配置1架A型无人机和2架B型无人机，其协同作战能力为0.98，我方无人机增援率为0.6和0.8，敌方无增援，则双方兵力动态变化如图4所示。

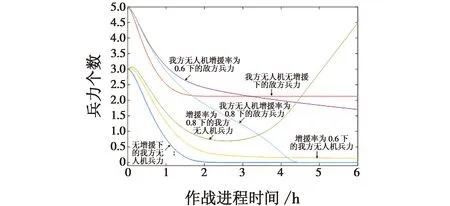
图4 不同增援率下双方兵力变化曲线Fig.4 Changing of force strength of two sides under different reinforcement rates

由图4可见，采用3架无人机编队作战，在无增援的情况下我方兵力被完全消灭，敌方最终剩余大约2个兵力；当增援率设置为0.6时，我方剩余兵力稍微有所提高但并没有改变战局；当增援率设置为0.8时，我方最终取得胜利。因此设置合理的增援率能够显著地改变战局，分析增援率对作战进程的影响能够帮助指挥决策人员做出正确的战术决策。以下对最优增援时刻点进行分析。

采用3架无人机编队作战，设增援率为0.8，增援时刻T分别为0，0.5，1，1.5和2，得到双方兵力变化曲线如图5所示。

图5中，靠近上方的曲线簇为不同增援时刻敌方兵力变化，靠近下方的曲线簇为我方无人机兵力变化。可以看到，在增援率相同的情况下，选择不同的增援时刻对战局的影响也不同。当增援时刻T分别为0，0.5和1.0时，其对战局的影响不大，均能够保证我方胜利。但是当增援时刻T分别为1.5和2.0时，由于增援时间较晚，在有限的作战过程中并不能改变战局。通过以上分析可以确定，在增援率固定的条件下，存在一个有效的增援时间点，在这个时间点之前进行增援能够有效地改变战局，减少我方作战兵力的损失。

根据以上分析，在实际作战中，可以通过数值计算的方法进一步细分增援时刻点，并计算这些增援时刻点下的我方兵力变化，从而为指挥决策人员提供更全面的辅助决策信息。

4 结论

针对无人机作战进程预测问题，基于经典兰彻斯特线性律，设计了无人机协同作战兰彻斯特方程，并考虑增援情况和载荷变化对无人机协同作战兰彻斯特方程进行了扩展。最后，对无人机协同作战进程预测进行了仿真，分别分析了作战双方兵力损耗过程、载荷变化对作战进程的影响以及战斗增援对作战进程的影响。仿真实验说明，本文所设计的无人机协同作战兰彻斯特方程能够有效地对无人机协同作战进程进行预测，将无人机协同作战与效能评估及作战预测进行一体化集成，为指挥决策人员提供更全面的辅助决策信息，具有较好的应用前景。