导数求函数零点存在区间取点探析*

☉甘肃省白银市第九中学 张永兵

对于函数零点的问题，不管正向还是逆向，思路都是一致的，根据函数的导函数讨论函数单调性，然后找到极值，再根据函数的零点存在定理，找到符合题目条件的情况进行分析.下面通过例题来举例说明.

（1）若a=3，求f（x）的单调区间；

（2）证明：f（x）只有一个零点.

（2）由于x2+x+1＞0，所以f（x）=0等价于

综上，f（x）只有一个零点.

探析：计算f（3a+1），f（3a-1），这一步非常巧妙，你是怎么想到的？

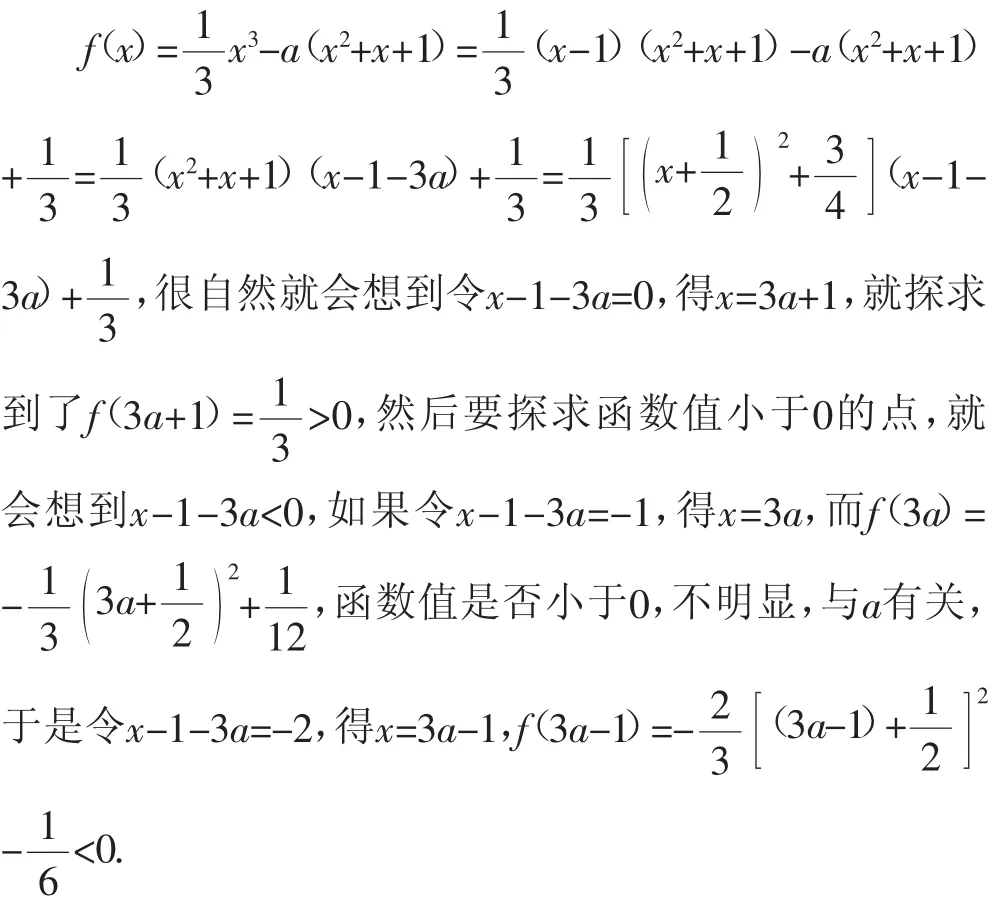
例2（2017年全国卷Ⅰ）已知函数f（x）=ae2x+（a-2）ex-x.

（1）讨论f（x）的单调性；

（2）若f（x）有两个零点，求a的取值范围.

解：（1）易知，若a≤0，f（x）在（-∞，+∞）上单调递减；若a＞0，f（x）在（-∞，-lna）上单调递减，在（-lna，+∞）上单调递增.（过程略）

（2）（i）若a≤0，由（1）知，f（x）至多有一个零点.

（ii）若a＞0，由（1）知，当x=-lna时，f（x）取得最小值，最小值为（f-lna）=1-+lna.

①当a=1时，由于（f-lna）=0，故（fx）只有一个零点；

综上，a的取值范围为（0，1）.

例3（2016年全国卷Ⅰ）已知函数f（x）=（x-2）ex+a（x-1）2.

（1）讨论f（x）的单调性；

（2）若f（x）有两个零点，求a的取值范围.

解：（1）易知，当a≥0，f（x）在（-∞，1）上单调递减，在（1，+∞）上单调递增.

（2）①设a＞0，则由（1）知，（fx）在（-∞，1）上单调递减，在（1，+∞）上单调递增.

又（f1）=-e，（f2）=a，取b满足b＜0且b＜ln，则（fb）＞，所以f（x）有两个零点.

②设a=0，则（fx）=（x-2）ex，（fx）只有一个零点.

综上，a的取值范围是（0，+∞）.

例4（2015年全国卷Ⅰ）设函数（fx）=e2x-alnx.

（1）讨论（fx）的导函数f（′x）的零点的个数；

解：（1）（fx）的定义域为（0，+∞），f（′x）=2e2x-（x＞0）.当a≤0时，f（′x）＞0，f（′x）没有零点；

当a＞0时，因为y1=e2x单调递增单调递增，所以f′（x）在（0，+∞）上单调递增.又f′（a）=2e2a-1＞0，当b满足时，f′（b）＜0，故当a＞0时，f′（x）存在唯一零点.

因为f′（x）在（0，+∞）上单调递增.f′（a）＞0，所以选取的b应小于a，并且越远离a，满足f′（b）＜0的可能性越大，取以当a＞0时至少有一个成立.其实b也可以取得0＜a＜4ln4.当a≥4ln4，可以利用a范围采用参数放缩法不含参数并且递增