雷电过电压作用下智能电表损坏概率估算
,,, ,,,,付存
(国网山东省电力公司 电力科学研究院,济南 250002)
0 引言
与传统机械式电表相比,除了具备基本计量功能外,智能电表还具备通信功能、自动调整功能,有效确保电能的稳定供应,在智能电网普及的当下得到越来越广泛的应用[1]。配电线路抵御雷害能力较弱,当线路遭受雷电直击或线路附近发生雷击时,线路上产生的过电压可达几百kV[2],雷电过电压沿线路侵入设备终端,极易损坏智能电表等低压采集设备,影响电能计量,甚至造成电表烧毁[3-4]。
电能表等低压设备的浪涌抗扰度试验多采用8/20 μs电流波或1.2/50-8/20 μs组合波[5]。当配电线路上产生雷电过电压后,过电压沿线路向低压侧传播过程中波形会产生多次折反射[6],呈现较为明显的振荡,而非呈简单脉冲状,实测线路雷电过电压波形[7]也证明了这一点,为此有必要分析实际雷电过电压作用下智能电表损坏概率。
EMTP[8]等软件能够考虑线路和设备结构特征,较为精确计算线路雷电直击过电压,但无法直接计算线路雷电感应过电压。Hoidalen[9]通过软件自带model模块编程计算感应过电压,Nucci等人[10]通过建立感应过电压计算程序LIOV与EMTP接口,解决了这一困难,计算结果精度较高。
笔者通过EMTP软件计算线路雷电直击过电压和感应过电压,利用蒙特卡洛模拟估算线路雷电过电压作用下智能电表损坏概率。讨论雷电回击速度对智能电表终端过电压的影响,分析变压器低压侧安装避雷器、智能电表终端安端SPD对电表损坏概率的影响,为智能电表的雷电过电压防护提供参考。
1 雷电过电压计算
1.1 雷击区间
智能电表是否发生损坏是一次随机过程,受到雷电流幅值、雷击点方位等因素影响。将这些因素对应的随机变量作为损坏概率函数的自变量,利用蒙特卡洛模拟[11]判断随机变量的值是否满足损坏智能电表的条件。通过对多次模拟结果的统计,得到损坏概率估计值。
考虑到可能影响雷电过电压形成的随机过程,将损坏概率y作为若干随机变量的函数:
y=f(i,d)
(1)
式中:i为雷电流幅值;d为雷电下行先导距线路水平距离。
对相关参数进行随机抽样,第k次抽样结果记为
yk=f(ik,dk)
(2)
若第k次抽样满足损坏电表的条件,即智能电表终端过电压超过其冲击耐受电压,则记yk=1,否则记yk=0。进行n次独立重复试验,根据大数定理,当n充分大时,智能电表损坏概率近似为
(3)
根据电气几何模型(EGM)[12]判断线路是否遭受雷电直击。对于幅值为ik的雷电流,导线雷击距计算公式为[12]
(4)
式中:Rc为导线雷击距;h为导线高度。
地面雷击距计算公式为[13]
Rgk=[0.36+0.168ln(43-h)]Rck
(5)
雷击地面的临界距离:
(6)
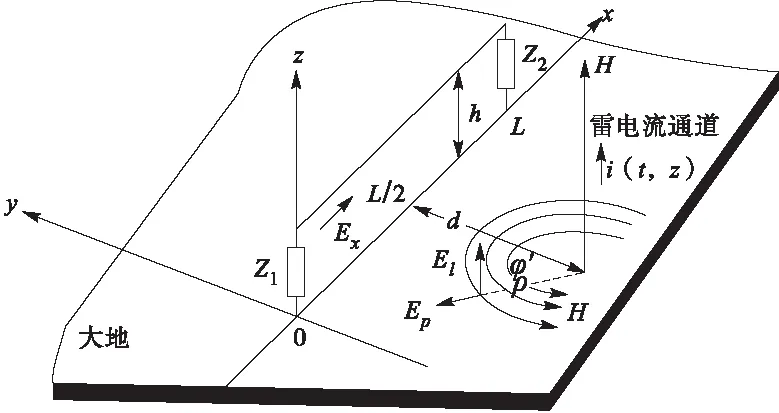
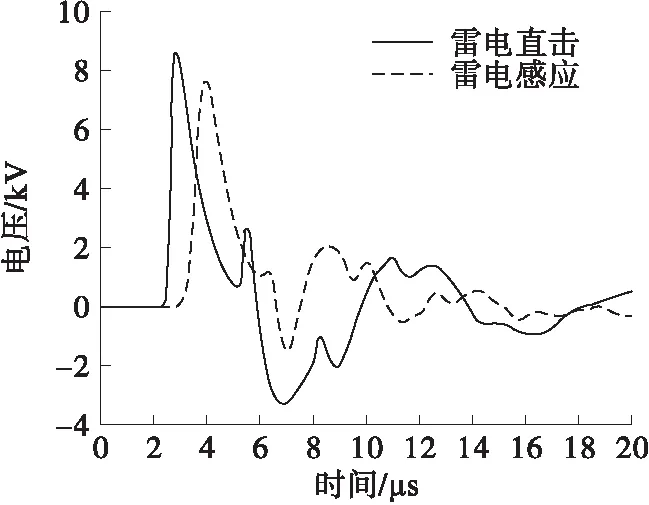
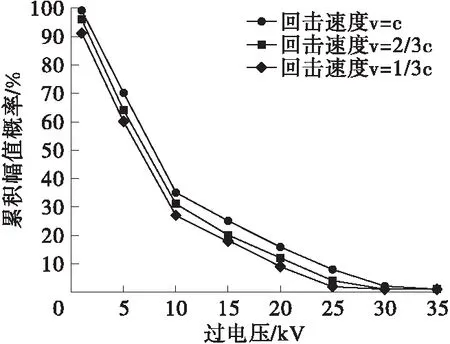
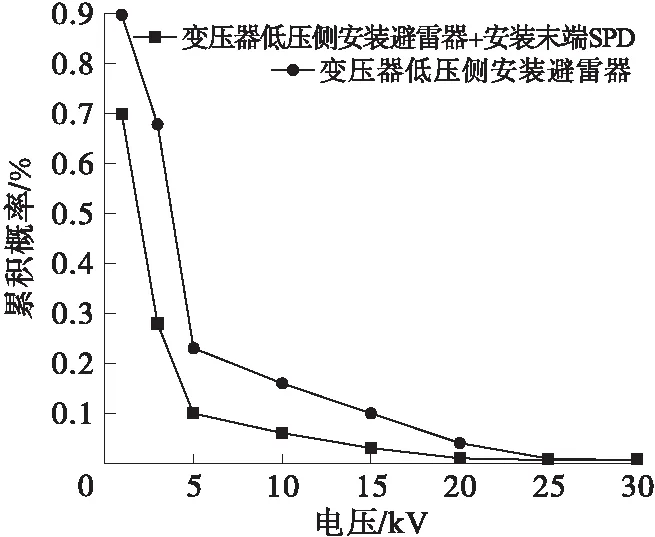
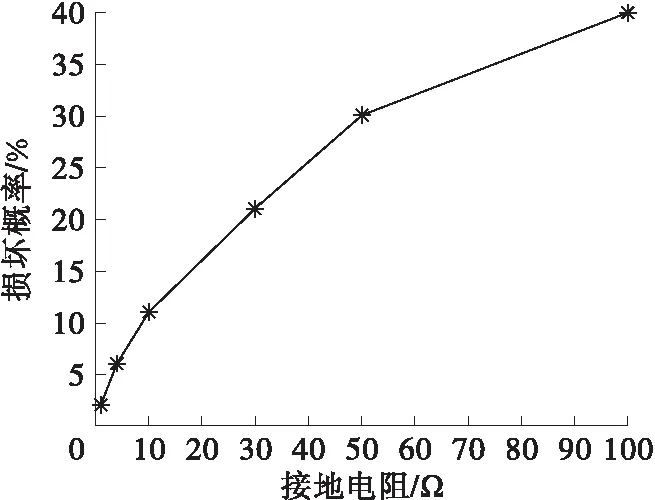
当dk 图1 雷击区间判断Fig.1 Direct lightning zone and indirect lightning zone 根据相关规范[13],雷电流幅值分布概率服从下式: (7) 式中,ī和σlni分别为首次回击电流幅值均值和标准偏差对数值,取30和0.53。 每次模拟产生一个服从[0,1]均匀分布的随机数,根据雷电流幅值分布概率公式便对应获得一个随机雷电流幅值ik。 雷电下行先导距线路水平距离d在[0,smax]区间内服从均匀分布,根据均匀分布公式便对应获得一个随机水平距离dk。 线路雷感应过电压计算主要考虑雷电流模型、电磁场传播模型和场线耦合模型,计算模型见图2。计算过程中将大地简化为理想导体即电导率无穷大[14]。 图2 雷电感应过电压计算示意图Fig.2 Configuration of the calculation model of lightning induced overvoltage 雷电通道底部电流波形选用较为符合实际的Heidler模型,其表达式为[13] (8) 式中:I0为雷电流幅值;τ1和τ2分别为电流上升和衰减时间常数;n与雷电流陡度有关,IEC标准推荐取10。 回击通道中雷电流的传输被等效成为一个向上传输的行波及其关于地面的镜像。回击模型考虑回击阶段中电晕电荷作用,采用指数衰减传输线模型(MTLE),雷电流随着通道高度呈指数衰减[15]。任意高度z和任意时间t的通道电流表达式为 i(z,t)=i(0,t-z/v)e-z/λ (9) 式中:i(0,t)是雷电通道底部电流波形函数;v为回击电流传播速度[14];λ是沿雷电流通道的电流衰减常数,取2 km[15]。 雷电流产生的空间电磁场计算采用偶极子法,将电流通道分解为无穷多个电偶极子,同时考虑其地面镜象影响[16],电流元产生的电磁场沿整个电流通道积分求得空间任意一点处电磁场。 根据Agrawal耦合模型,线路感应过电压通过入射场电压和散射场电压叠加而得,具体表达为[14] V(x,t)=Vi(x,t)+Vs(x,t) (10) 入射电压Vi(x,t)表达如下: (11) Agrawal耦合模型中散射电压Vs(x,t)转化为时域时表达如下: (12) 式中,L和C分别为线路单位长度的电感和电容。边界条件为Vs(0,t)=-Z1I(0,t)-Vi(0,t),Vs(L,t)=Z2I(L,t)-Vi(L,t);Z1和Z2分别为线路两端阻抗。 对电磁场分量进行相应化简以求解线路感应过电压。在高度z=h处水平电场为 (13) 沿z方向电场: (14) 当线路末端阻抗匹配时,观测点x处感应过电压的计算公式可简化为[13]: (x,t)=0.5[A0(x,t)-bA0(x,t-tf)] (15) 图3给出了EMTP中感应过电压计算电路模型。两段type51型RL线路模型表征配电线路匹配波阻抗,下端的4个类型type60电源表征线路观测点处雷电感应过电压[8]。 图3 感应过电压计算电路模型Fig.3 Model to calculate lightning induced voltages 图4给出了一个简单的配电线路结构模型,包括10 kV架空线路、10 kV/220 V配电变压器、220 V线路和终端智能电表。 图4 配电线路结构模型Fig.4 Configuration of the distribution power system 10 kV线路采用LGJ-50钢芯铝绞线,三相高度分别为9.6 m、8.2 m、8.2 m,档距50 m。考虑雷电流高频特性,采用高频变压器模型[17],具体等效模型见图5。 图5 变压器高频模型Fig.5 High-frequency model of the transformer 智能电表内部电路结构较为复杂,主要分析其控制电路供电电源过电压侵入特性,采用变压器、整流桥和稳压芯片表示[18]。 仿真中采用非线性电阻模拟金属氧化物避雷器,其流经电流与电压之间服从下式关系: i=kuα (16) 式中:i为流经避雷器的电流;u为避雷器上电压;系数k和α根据避雷器产品具体数据拟合得到。 图6给出了距10 kV线路垂直100 m处发生雷击时,智能电表终端过电压波形,雷击点距变压器水平距离500 m,220 V线路长度取100 m。雷电流波形为2.6/50 μs[19],雷电直击线路时抽样雷电流幅值为32 kA,雷击线路附近地面时抽样雷电流幅值为43 kA,回击速度取2×108m/s。 图6 智能电表终端雷电过电压波形Fig.6 Waveform of lightning overvoltage of the smart meter 由图6可看出,无论是雷电直击线路还是线路雷电感应,智能电表终端过电压波形均存在较为明显的振荡。抽样雷电流幅值较低情况下,智能电表终端雷电直击过电压仍然高于雷电感应过电压,且两种情况下过电压均超过了配电系统中IV类设备冲击耐受电压6 kV[19],导致智能电表损坏。较高的过电压幅值加上较陡的波头,导致过电压变化率过高,也不利于智能电表的防护。 图7给出了不同回击速度下,智能电表终端过电压累积幅值概率分布曲线。 由图7可看出,随着回击速度的增加,智能电表终端过电压累积幅值概率分布曲线整体右移,即出现幅值高的过电压概率增大。回击速度影响线路雷电感应过电压,回击速度越高,回击电磁场强度越大,线路耦合产生过电至智能电表终端过电压也越大。 图7 回击速度对智能电表过电压累积幅值概率分布曲线影响Fig.7 Cumulative-probability distribution of lightning overvoltage of the smart meter vs current wave propagation speed 为了抑制线路高压侧传递过电压,变压器低压侧常常安装避雷器。即使低压侧安装避雷器,过电压受终端设备与连接线路阻抗之间的谐振影响,终端过电压幅值仍然可能较高[20]。图8给出了变压器低压侧安装避雷器和同时在智能电表终端安装SPD情况下,智能电表终端过电压累积幅值概率分布曲线。10 kV线路避雷器型号为YH5W-17/50,终端SPD直流参考电压U1mA为264 V,2 kA电流冲击下残压为500 V,接地电阻10 Ω。 图8 安装避雷器后智能电表过电压累积幅值概率分布曲线Fig.8 Cumulative-probability distribution of lightning overvoltage of the smart meter after installing arresters 由图8可看出,安装避雷器后,过电压累积概率分布曲线整体左移,幅值高的过电压出现概率显著降低。变压器低压侧和电表终端同时采取防护后,智能电表损坏概率降低更为明显,由24%降为11%。此外,两种保护方式下累积幅值概率均出现突然降低情况,这是由避雷器的限压作用引起的。 图9给出了变压器低压侧安装避雷器且智能电表终端安装SPD情况下接地电阻对智能电表损坏概率影响曲线。 图9 智能电表损坏概率随接地电阻变化Fig.9 Failure probability of the smart meter vs grounding resistance 由图9可看出,智能电表损坏概率随着接地电阻的增大而显著增加。接地电阻为4 Ω时,损坏概率仅为2%,接地电阻增大至50 Ω时,损坏概率便接近1/3,因此需要尽可能降低避雷器接地电阻。 利用蒙特卡洛模拟计算线路雷电过电压作用下智能电表损坏概率,得到结论如下: 1)智能电表终端过电压波形存在较为明显的振荡,且波头时间较短,过电压幅值较高,可能超过智能电表冲击耐受电压。 2)智能电表过电压累积幅值概率分布曲线随着回击速度的增大而整体右移,智能电表损坏概率增加。 3)变压器低压侧和电表终端安装过电压保护设备后,智能电表损坏概率大幅度降低。 4)接地电阻对智能电表损坏概率影响非常大,需要尽可能降低避雷器接地电阻以减小电表损坏概率。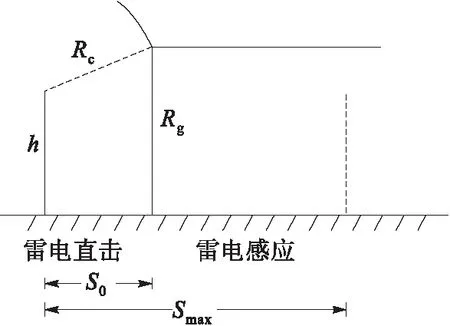
1.2 线路雷电感应过电压计算

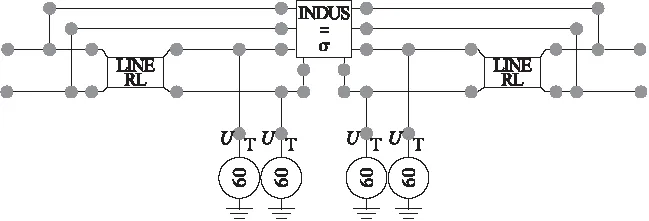
1.3 配电系统模型


2 仿真结果分析
2.1 智能电表终端过电压波形
2.2 回击速度影响
2.3 安装避雷器效果
2.4 接地电阻影响
3 结论

