8/20 μs雷电流冲击下铜导线崩断和熔断特性的分析
,, ,
(南京信息工程大学 气象灾害预报预警与评估协同创新中心,南京 210044)
0 引言
雷击事故每年都会给人们的生命财产造成巨大损失,而造成这些损失的主要原因之一就是各种形式的雷电过电流[1-3]。雷电过电流流经导体时会伴随着机械效应和热效应,造成输电线路崩断或熔断现象。在对雷电过电流造成的事故现场进行评估时,流过输电线路雷电过电流的大小是一个重要的评估参数。
目前,国内外学者对雷电流损坏机理的研究重点在雷电流的机械效应和热效应两方面。国内学者刘毅彬等人对东莞地区2009年至2011年10 kV配网导线的断线数据进行分析时发现,雷击事故和设备缺陷是导线断线的主要原因[4];张小青指出,雷电流的机械效应主要体现在电磁力和内压力两方面。当雷电流流经两根相近的导体时,雷电流产生的电磁力可能使两根导体相互吸引或排斥,当斥力或引力足够大时可造成导体变形或损坏,同时瞬态的雷电流使导体快速升温膨胀,导致导体炸裂[5]。而他在计算雷电流直接与金属物接触情况下的雷击点以及金属其它位置产生的温升时,通过对雷电流持续时间内的能量积分,在极短时间内忽略温散的影响推导出了温升公式,并指出当温升值过高时,就会造成金属熔化[6]。国外学者John S. Schaffer在分析线导体通过瞬态电流产生热效应时,提出了熔化决定因子的概念,指出当通过导线的过电流过大以至于导线再次冷却成为不可能时,导线的状态由熔化决定因子确定,且为一个特征值,仅与导线的种类有关[7]。以上学者均对雷电流流经导体时的损坏机理做了大量工作,而笔者通过对一种工频载流量不同的黄铜线进行8/20 μs波形雷电流冲击试验发现,冲击电流逐渐增大时,铜线均是先崩断,当冲击电流继续增大到一定程度后,铜线才发生熔断现象,且对于不同长度铜线实验现象基本一致。所以,笔者试验得到规律关系式具有重要的现实意义。
针对以上情况,笔者通过对导线通过瞬间大电流瞬间导体受到的机械效应和热效应的理论分析,选取一种材质相同工频载流量不同的黄铜线,分别取7 cm和13 cm两种长度进行8/20 μs波形雷电流冲击试验,比较两种长度铜线崩断和熔断冲击电流临界值。对所得试验数据作图并拟合分析铜线崩断和熔断冲击电流临界值与其工频载流量之间的关系式,为雷电过电流损毁铜芯输电线事故的现场评估提供一定的参考依据。
1 理论分析
铜导线在雷电流冲击下会产生崩断和熔断两种情况。这是因为雷电流通过导体时会产生机械效应和热效应,下文将分别对雷电流通过导体产生的机械效应和热效应进行分析。
1.1 雷电流通过导体产生机械效应原理
一段长为l,载流量为I的导线,在均匀磁场B中所受的力可由安培公式确定[8-9],即
F=Il×B
(1)
式中:F为安培力,普遍认为安培力是带电粒子在磁场中定向漂移所受的洛伦兹力的宏观表现。但近十余年来,有学者对上述观点提出了异议,认为载流导线中定向漂移的带电粒子(以电子为例)在磁场中受洛伦兹力的影响会发生侧向偏转,从而在导体两侧出现异种电荷,在导体内部形成一个电场,称为Hall电场,见图1,记作EH,有
(2)
式中:e为电子电量;n为自由电子数密度;j为电流密度;R为Hall电场系数,R=1/en。对于电子导体,R<0,Hall电场施力于导体晶体点阵,这就是安培力。但是,上述两种观点都是不全面的,没有考虑导体材料本身的性质。

图1 Hall电场示意图Fig.1 Schematic diagram of the Hall electric field
当电子的运动速度v远小于真空光速c时,在晶体点阵的周期势中其运动方程为
(3)
一般地
(4)
式中:h为普朗克常量;k为一个特定波矢。电子受到正离子点阵一个作用力为f′,故
(5)
这意味着导体中的传导电子一般不是完全自由的。这样,作用于传导电子上的合力为
fe=-eE-ev×B+f′
(6)

(7)
式中,vd为点阵定向漂移速度。

(8)
(9)
1.2 雷电流通过导线热效应理论分析
当导体通过一个比最小冲击熔化电流大得多的雷电流时,导体的局部或整体达到熔化温度,在很短的时间内熔化甚至燃烧。由于雷电流的作用时间很短,在计算雷击点处的温升以及雷电流通过金属体所产生的的温升时,均可忽略散热的影响。在没有热传递的条件下,雷电流通过导体的任意一部分,在任何瞬间的温度上升率为[10-14]
(10)
式中:W为瞬时供给单位体积的功率,J;m为单位体积质量,kg;C导体比热,J/(kg·℃)。
实际上,上式给出的能量只供给导体材料熔体部分使熔体升温,其他部分保持温度不变。供给熔体材料单位体积能量等于通过单位体积瞬时电流二次方与电阻的乘积。电阻是与温度密切相关量,可近似表示为
R=R0(1+αT)
(11)
式中:R0为导体室温电阻;α为室温下电阻温度系数;T为室温下,单位体积导体的温升。由以上两式可得任意时刻温度
(12)
每单位体积通过雷电流随时间变化的变量可知,那么等式可解。对于通过雷电流的线导体,所有部分情况相同,因此,确定线导体达到熔点温度所需要的时间,可以由上式求出。
导线熔化决定因子I2t的量是通过线导体的瞬间电流值的平方对时间的积分,这个时间是从雷电流流经导体开始至导体燃弧熄灭为止的整个时段,即

(13)
如果在上述整个时段内,线导体的电阻维持不变,那么,I2t的值正比于消耗的能量。事实上,由于过电流产生的热量常常使线导体的电阻明显增大。I2t是一个特征量,只取决于导线的种类。当通过导线的瞬间电流足够大,导线的状态更依赖于I2t的值的大小。
2 试验分析
2.1 载流量计算
依据IEC-60364-5-523铜芯电线电缆载流量标准[15],铜导线载流量与导体截面积之间有如下关系:
I=A·Sm-B·Sn
(14)
式中:I为载流量,A;S为导体的标称截面积,mm2;A和B为系数m和n为指数,均视电缆类型和敷设方式而定
对于截面积小于等于16 mm2的单芯导线,A取13.5,m取0.625,B取0,因此可以得到试验选用的铜导线载流量数据见表1。

表1 不同规格铜线的工频载流量Table 1 The current carrying capacity data of different specification brass wires
2.2 试验方法及测试数据
首先,选取同一种材质黄铜导线,对不同工频载流量的铜导线,分别取7 cm和13 cm两种长度通过8/20 μs雷电流冲击平台(ICGS)做雷电流冲击实验。对每根铜导线进行实验,逐渐增加冲击电流的数值直至铜导线熔断或崩断。每次冲击后更换一根完全相同规格的铜导线以确保实验的准确性,找到每一种铜导线崩断或熔化的临界电流值,并以此临界电流值冲击3根相同的铜导线,验证每个临界点的电流值的有效性。线导体在通过冲击电流时所受的横向电场力在实验室条件下不可测,因此,根据不同工频载流量的铜导线在8/20 μs雷电流冲击下的现象,选取其中直接崩断铜导线,用万能拉伸机对其进行拉伸实验,得出每根铜导线的最大崩断力,即用铜线的纵向耐受拉力的大小来反映其遭受冲击雷电流时受到的机械力的大小。最后,得出不同工频载流量的铜导线的实验数据见表2。
从表2数据可以看出:同种规格的铜线熔断电流值大于崩断电流值;相同工频载流量而长度不同的两根铜线的崩断电流值相差很小,同样的,熔断电流值也相差不大。因此,笔者认为铜线的长度对冲击崩断电流值和熔断电流值影响不大。

表2 不同工频载流量铜导线试验数据Table 2 Test data of the brass conductors with different frequency current carrying capacity
2.3 铜导线试验现象分析
使用2台ICGS进行试验,其中小平台可产生5~60 kA的8/20 μs雷电冲击电流,大平台可产生20~160 kA的雷电冲击电流。铜导线的雷电冲击试验见图2。

(a)崩断为多段

(b)崩断临界点

(c)断为多段且部分小段熔化变形(熔断临界点)
图2(a)所示为13 cm铜导线崩断多段状态,各分段铜导线保持完好圆润,且分段总长度与未崩断前一致,因此,造成这种状态的冲击电流大于铜线的冲击崩断临界电流值而小于其冲击熔断临界电流值。逐渐减小造成该状态的冲击雷电流值以寻找各个规格铜导线恰好崩断时的冲击雷电流值,即临界冲击崩断电流值。图2(b)为铜导线恰好崩断时的状态,整根铜导线保持完好,只有一处断点。从图2(c)可看出铜导线断为许多很短的小段,且部分小段熔化为不规则形状,经过多次试验发现,当冲击电流值小于该状态下冲击电流时,铜导线仅崩断为规则小段,所以本文认为该状态下的冲击雷电流即为该规格铜导线的熔断临界冲击电流值。图3为部分规格铜导线雷电流冲击试验图。

(a)工频载流量为14.58 A的铜导线未崩断冲击电流

(b)工频载流量为14.58 A的铜导线崩断临界冲击电流

(c)工频载流量为14.58 A的铜导线崩断为多段时冲击电流图3 铜导线雷电流冲击试验图Fig.3 Pictures of lightning current impact tests
2.4 铜导线崩断和熔断现象分析
通过对不同规格铜导线的大量试验发现,所有规格铜导线在冲击电流从小到大变化过程中均是先发生崩断现象,当冲击电流继续增大到一定程度才会发生熔断现象。当冲击电流达到铜导线的冲击电流崩断临界值时,铜导线因受到机械力FM的作用而直接崩断,这种现象符合导体通过雷电流会受到机械力作用理论。当冲击电流继续增大时,铜导线会断为多段,见图2(b),此时各段完整,没有烧熔迹象,总长度与原铜导线一致。随着冲击电流继续增大,铜导线会崩断为更短的小段,直到部分小段开始出现不规则烧熔迹象,见图2(e),笔者认为此时即为铜导线冲击熔断电流临界值。
将不同工频载流量的铜导线的崩断电流临界值和熔断电流临界值绘制成曲线,并对各试验曲线分别进行线性拟合,得到各拟合方程,见图4。
图4(a)的拟合曲线为
y=-15.107+4.829x
(15)
图4(b)的拟合曲线为
y=-14.868+4.876x
(16)
图4(c)的拟合曲线为
y=-15.232+5.077x
(17)
图4(d)的拟合曲线为
y=-13.804+5.065x
(18)
式中:x为工频载流量,A;y为冲击电流,kA。
图4(a)和图4(b)两条曲线的拟合曲线相关系数R2分别为0.997 8和0.998 6,图4(c)和图4(d)两条曲线的拟合曲线相关系数分别为0.997 0和0.996 8,四条拟合曲线的相关系数都非常接近1,所以将拟合曲线用于分析实测数据的曲线走势及散点分布情况是合理的。从图4可以看出,铜导线的长度对崩断电流临界值以及熔断电流临界值影响不大;铜导线的崩断电流临界值以及熔断电流临界值与其工频载流量呈正相关关系。
由于铜导线在通过冲击电流时发生崩断现象符合导体遭受雷电流会受到机械力作用理论,根据表2所得数据画出铜线崩断时所受最大崩断力与工频载流量的关系曲线,见图5,拟合方程为
y=-52.894+36.900x
(19)
式中:x为铜导线的工频载流量,A;y为最小崩断力,N,拟合相关系数R2为0.994 9,所以拟合曲线是合理的。由图5曲线可知,铜导线冲击崩断机械力与工频载流量呈正相关。这解释了随着加在铜导线两端的冲击电流的增大,铜导线崩断越严重的现象。

(a)7 cm铜导线崩断电流临界值

(b)13 cm铜导线崩断电流临界值

(c)7 cm铜导线熔断电流临界值
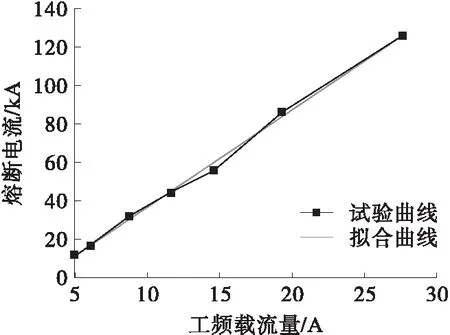
(d)13 cm铜导线熔断电流临界值
通过以上分析,根据铜导线载流量与冲击崩断或熔断电流临界值的关系,可以评估某种规格铜导线在遭受雷电过电流发生崩断或熔断现象时通过铜导线的雷电流最小值,对事故现场雷电流大小的评估有一定的现实指导意义。

图5 铜导线最小崩断力与工频载流量的关系Fig.5 Relationship between the minimum breaking force and frequency current carrying capacity of the brass wire
3 结论
针对雷电流侵入铜芯输电线时造成铜线崩断或熔断问题,笔者通过对同种材质不同截面积铜线进行8/20 μs雷电流冲击试验,找出不同工频载流量的黄铜线崩断或熔化冲击电流临界值,得到结论如下。
1)当雷电流通过铜线时,所有规格铜线均是先崩断,当雷电流大到一定程度时,铜线才会发生熔断现象。
2)铜线在8/20 μs雷电流冲击下崩断时受的力,符合横向电场力和所有定向漂移电子对铜线施加的反作用力的矢量和为铜线所受的机械力理论。
3)当冲击铜线的8/20 μs雷电流足够大时,铜线发生熔断现象符合当通过导线的瞬间电流足够大,导线的状态取决于导线熔化决定因子值的大小的理论。
4)对于长度不同而工频载流量相同两根铜线,它们的崩断和熔断电流临界值相差不大,且崩断和熔断电流临界值以及铜线所能承受的机械力与铜线的工频载流量均呈正相关。

