基于Romax的风电机组主轴轴承接触应力分析

付大鹏，褚加瑞

(东北电力大学 机械工程学院，吉林 吉林 132012)

我国对大型风力发电机组中一些关键技术的研究还十分薄弱[1].沈德昌等[2]指出，轴承是风电机组中的薄弱环节，也是主要故障点之一.近年来，在滚动轴承接触应力的研究中，无齿轮箱的直驱式风电机组主轴轴承的研究涉及很少.杜静等[3]使用Gap单元模拟主轴轴承滚子，无法体现轴承在整个轴系中的受载情况.黄炜斌等[4]建立球轴承转子系统动力学分析模型，主要研究了接触角与内外圈沟曲率系数对系统动态特性的影响.吉博文等[5]采用Romax软件对轴承试验台建模仿真，分析了多种结构参数对疲劳寿命的影响，但缺少对轴承工作游隙的考虑.

本文以1.5 MW直驱式风电机组主轴轴承的后轴承为研究对象，首先建立轴承内部载荷分布的几何模型，推导出关于游隙与载荷分布之间更为细致的数值计算过程，并在Romax Designer14.5平台上建立了一套定轴系统模型.通过调节轴承运行游隙得出滚子、滚道的应力大小和分布规律.在Romax软件的轴承数据库中，不仅可以直接选择需要使用的轴承，同时也可以自定义轴承，便于修改轴承内部结构和工况环境，这对于研究轴承接触应力的影响因素及影响大小提供了便捷有效的途径[6].所以，在应用Romax软件时，该方法不仅符合直驱式风电机组主轴轴承的研究，也适用于所用滚动轴承.

1 轴承滚动体的接触载荷计算

风电机组主轴轴承后轴承是圆柱滚子轴承，作为滚子轴承，确定轴承载荷在滚动体之间如何分布，首先需要建立滚子与内外圈滚道接触的载荷-位移关系.Thomas和Hoersch[7]分析了集中接触问题的应力和变形.对于滚动轴承，一般有

Q=Kδn，

式中：球轴承，n=3/2；滚子轴承，n=10/9(≈1.11)；Q为轴承滚子所受载荷；K为载荷-位移常数；δ为滚子与滚道的接触变形.

建立具有内部游隙并且受径向载荷球或滚子轴承的几何模型，如图1所示.由于轴承最初是对称布置，游隙Gr同样是平均分布，如图1(a)所示.

图1 滚动体与套圈接触几何模型

对于径向载荷作用下的轴承，滚动体与滚道的接触位置会产生弹性形变，如图1(b)所示.任意角度位置滚动体的径向位移为：

δψ=δ0cosψ-Gr/2，

式中:δ0为ψ=0°的径向移动量.Harris和Kotzalas[8]提出了一个迭代的过程计算球和滚子中最大滚动体的载荷，并引入了载荷分布积分Jr(ε)和载荷分布系数ε.本文将给出更为细致的计算过程，为后文的Romax分析提供理论依据.

根据载荷-位移关系，任意位置角的接触载荷为

式中：

根据受力平衡，轴承受到的径向载荷等于每个滚子载荷的竖向分量之和

积分的形式即为

或

Fr=ZQmaxJr(ε),

所以，

其中：

对于风电机组圆柱滚子轴承，有

该计算方法对于轴承内的零游隙，正和负游隙都有效.

2 模型建立与仿真分析

2.1 模型的建立

为了使主轴轴承运行更符合真实状况，建立一套轴承定子系统模型.1.5 MW直驱式风电机组定子轴系的建模分为四步：

(1)定轴的建模；

(2)轴的基准与定位；

(3)轴段与疲劳特征的添加：依据轴基准建立阶梯偏置，形成不同轴段.在轴阶梯或轴肩位置，建立一些特征(圆角、凹槽及径向孔等)，便于进行疲劳分析.

(4)轴承的建模：1.5 MW主轴轴承在Romax数据库不存在，需要对其自定义，轴承设计参数如表1所示.根据Romax软件高级轴承模块自动生成需要的轴承内部参数，完成轴承定义.

表1 主轴轴承的主要设计参数

图2 仿真模型

2.2 模型的仿真

在Romax软件中完成1.5 MW直驱式风机定轴系统仿真模型，如图2所示.该机型主轴采用两点支撑，前轴承(BT轴承)是双列圆锥滚子轴承BT2-8168/HAIVK443，后轴承(NJ轴承)是单列圆柱滚子轴承NJ28/710 ECMA/VQ716.文中仅对承受发电机重量的后轴承进行研究分析.

仿真系统采用ISO VG 32 Mineral润滑剂，工作温度为40 ℃.模型中各轴承内圈固定，外圈分别给出初始轴向定位预紧量-200 μm，-150 μm.在后轴承所受的载荷谱中选择占时间比最长的工况进行研究，此时轴承所受的力Fz为163 000 N，Fy为385 000 N，X向扭矩为2 561 000 Nm.这种工况下后轴承的径向工作游隙选择初始游隙355 μm.

3 仿真结果与分析

在这种工况下，得出内外圈周向最大应力分布和滚子沿滚子长度方向的接触应力，如图3(a)所示.此时接触应力在滚子中心附近最大，远离滚子中心逐渐减小，从整个分布来看，接近抛物线状.文献[9]给出了Hertz线接触理论的应力分布，如图3(b)所示.其中横坐标x为轴承轴向，纵坐标为应力分布，α为接触椭圆区域的长半轴.由此可见，Romax分析结果与Hertz[10]弹性接触理论基本吻合，证明了利用Romax软件分析主轴轴承接触应力的可靠性.但此时，在滚子一端存在明显的边缘应力，严重损伤滚子的承载能力.

图3 分析结果与应力曲线对比

已知研究表明，游隙对滚动轴承的综合性能具有十分重要的影响[11].在安装和运行条件一定时，游隙大小决定着轴承的载荷分布和最大接触应力，并决定着轴承的疲劳寿命.游隙过小，会使轴承的内外套圈与滚子之间接触应力变大，增加轴承温升，导致其无法正常运行，过大的游隙则会引起轴承振动和噪声.因此存在最佳工作游隙，使得轴承内的接触应力最小，从而使疲劳寿命最长.

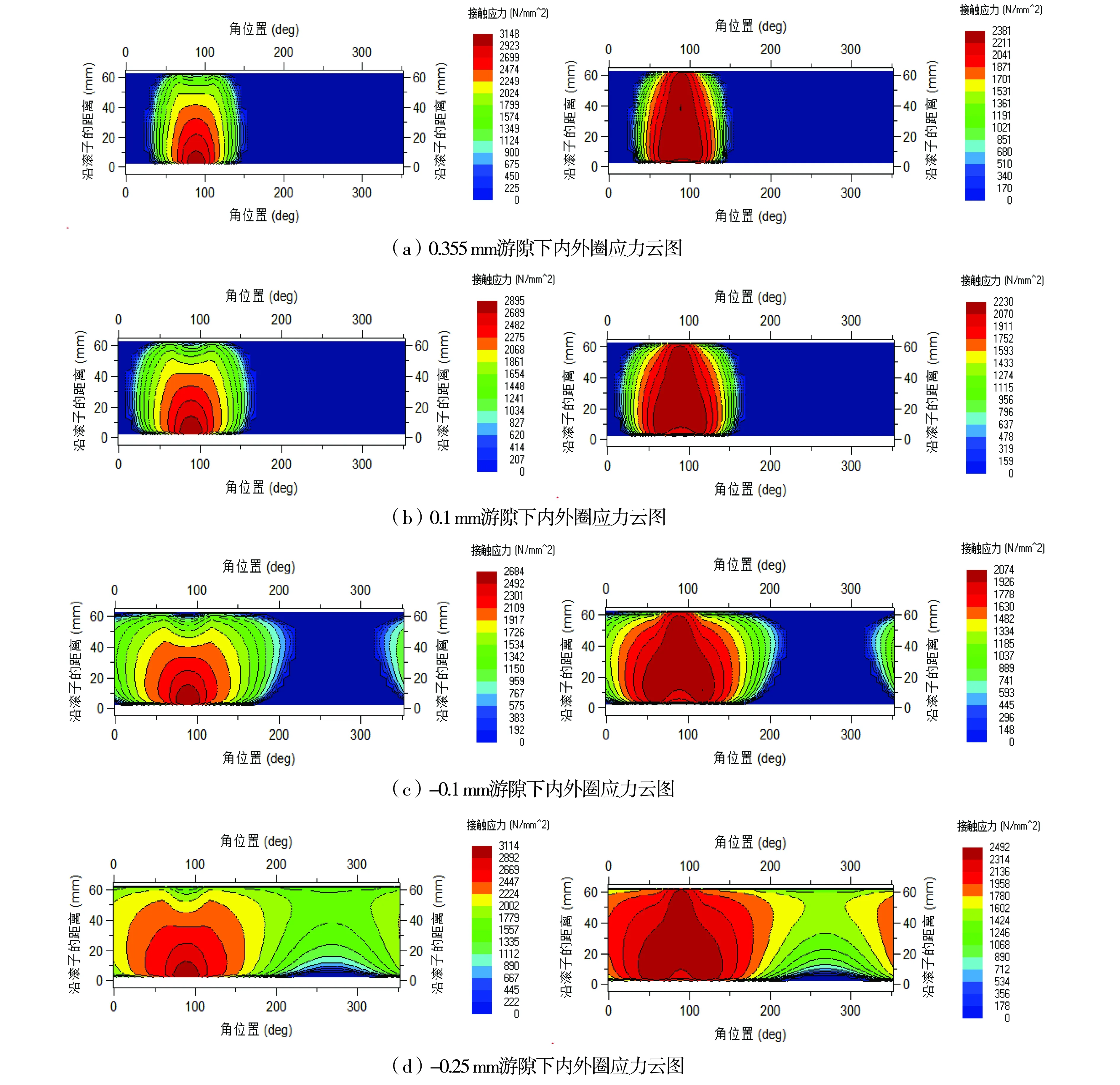
图4 内外圈接触应力云图

通过Romax软件，在相同的工况下，调节主轴轴承后轴承的工作游隙，工作游隙的选值从轴承的原始游隙逐渐减小，分别取0.335 mm、0.2 mm、0.1 mm、0 mm、-0.1 mm、-0.2 mm、-0.25 mm七种游隙，得到各种情况下内外圈的接触应力云图，四种情况下的云图，如图4所示.在Romax每个游隙下得到的最大接触应力与理论解的误差，如表2所示.

表2 不同工作游隙下滚子与内外圈最大接触应力

从表2中发现，利用Romax得到的结果与理论计算结果基本一致，再次验证了Romax软件分析主轴轴承接触应力的准确性.将Romax计算结果与等效工况下主轴轴承试验机测试结果进行比较，如图5、图6所示.可以看出，模拟结果与试验机测试结果基本一致，游隙的变化使轴承滚子与内外圈的接触应力也随之变化，由于模拟工况相对稳定，此时的接触应力值也相对较小，当径向游隙取一个小的负值时，轴承的内外圈的接触应力最小，从而能够提高主轴轴承的疲劳寿命.但从云图中发现，滚子的边缘应力现象并没有变化.

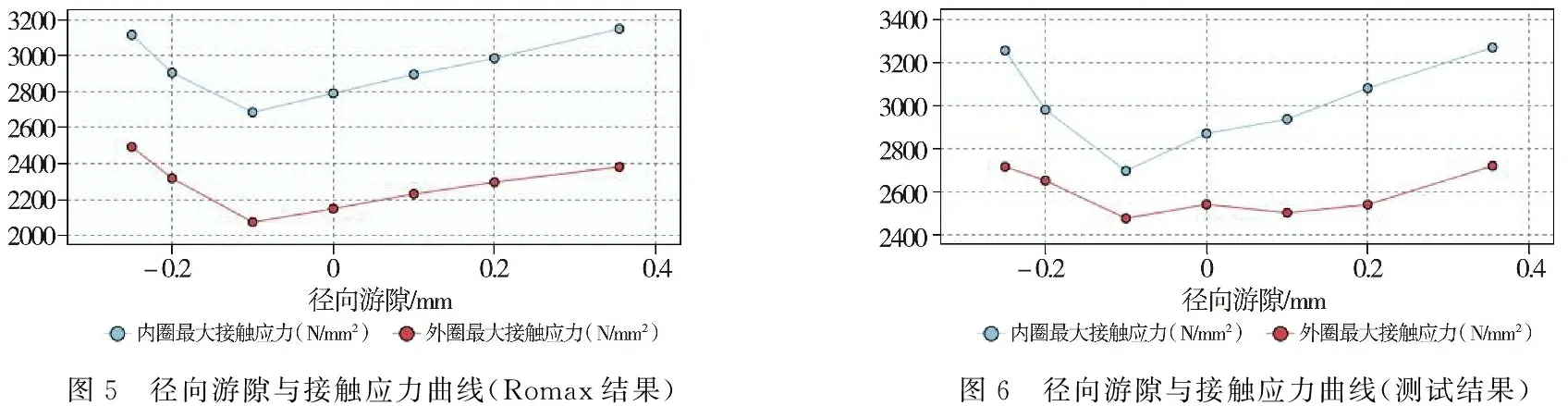
图5 径向游隙与接触应力曲线(Romax结果)图6 径向游隙与接触应力曲线(测试结果)

4 结 论

(1)利用Romax软件得到风电机组主轴轴承在不同的游隙下内外圈接触应力分布，与Hertz弹性接触理论计算结果以及试验机测试结果具有良好的一致性，表明了该方法的可靠性.为滚动轴承的接触应力分析提供一种快速有效的新方法.

(2)对比不同游隙对圆柱滚子轴承内外圈接触应力的影响，当1.5 MW直驱式风电机组主轴轴承有一个小的负游隙-0.1 mm时，可以使接触应力减小，游隙偏离此值时，都会增大接触应力.为滚动轴承最佳工作游隙的确定提供一定的帮助.