指标偏好DEA问题的研究及其应用

张 杰，孙晓宇，杜康吉

(东北电力大学 理学院，吉林 吉林 132012)

数据包络分析(Data Envelopment Analysis，DEA)理论是由 Charnes等在1978年提出的一种应用于运筹学与经济学领域中评价多输入多输出决策问题的非参数的数学方法[1].C2R模型是数据包络分析中的基本模型，它可以用来评价决策单元是否同时达到规模有效性和技术有效性[2].DEA方法不仅能对不同领域的问题进行评价，而且评价结果能够反映大规模的社会实验结果，使其在许多领域得到了发展及应用[3～5].随着研究的深入，不断有学者对其确定指标权重的方法提出质疑.传统DEA模型对指标权重无任何限制，它实际上是选取了对被评估决策单元最有利的权重，不能体现每个指标的重要程度，这样得出的结果可能不符合客观实际.对此国内许多学者都致力于传统DEA指标权重的理论研究，取得了显著的成果.

张茂勤、屈也频、弓晓敏等相继提出了在模糊集上具有某种偏好的DEA，并通过Campos指数将模糊集之间的关系转化为一般的线性关系，从而得到了一种可体现决策者意愿的输出量的模糊偏好修正方法[6～8]；郭存芝，彭泽怡等提出了对于评价多指标问题，给指标进行分级，并采用主、客观权重相结合的办法生成了DEA输入、输出综合指标[9]；亢磊磊和王琼相继将DEA与灰色关联分析相结合，对权重进行约束[10].但是这些基本理论模型共同的缺陷都是采用主观评价方法确定DEA模型权重，破坏了DEA的客观性.因此找到一种方法，既能保持DEA客观性，又能体现不同指标重要性的不同，显然具有现实意义.

鉴于此，本文针对多输入多输出的评价问题，考虑到各个评价指标之间的重要性的差异，构建了指标偏好DEA模型及其对偶模型，并对其有效性进行了研究.

1 指标偏好DEA模型的构建及性质

1.1 基于指标偏好的 DEA模型的构建

(1)C2R模型

假设有n个决策单元，每个决策单元都有m种类型的输入以及s种类型的输出，利用C2R模型得到n个决策单元的相对效率值.

max(μTYp)=Vp，

(1)

(2)指标偏好DEA模型(OC2R)

由于模型C2R中不能体现每个指标的重要程度的差异，基于此改进模型.对于每个待评价的决策单元中有m个输入指标和s个输出指标，根据决策者给出这m+s种指标的重要程度，在对输入指标进行排序时不妨假设m种输入指标的重要程度依次降低，同样对于s种输出指标的重要程度依次降低，即所对应输入和输出指标的权重ωT=(ω1，ω2，…，ωm)和μT=(μ1，μ2，…，μs)应满足

ωi-ωi+1≥0，i=1，2，…，m-1；μr-μr+1≥0，r=1，2，…，s-1，

即得到指标偏好DEA模型(POC2R)为

max(μTYp)=Vop,

(2)

(3)指标偏好DEA模型的对偶问题(DOC2R)

minθ=VOD，

(3)

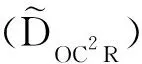
(4)

1.2 指标偏好DEA有效性(OC2R)定义

(1)若模型(OC2R)的最优解ω0，μ0满足Vop=μ0TYp0=1，则称决策单元p0为弱DEA有效(OC2R).

(2) 若模型(POC2R)的最优解ω0>0，μ0>0且满足Vop=μ0TYp0=1，则称决策单元p0为DEA有效(OC2R).

1.3 指标偏好DEA有效(OC2R)性质

定理1 模型(POC2R)存在可行解.

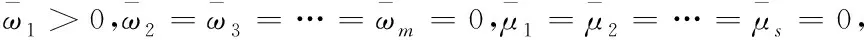
对于每个指标权重显然满足

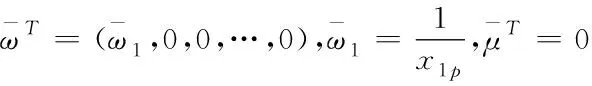
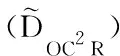
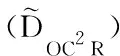
证明：假设(Xp0，Yp0)为DEA无效(OC2R)，即存在(Xp，Yp)∈T(d)使得

Xp0≥Xp，Yp0≤Yp，Xp0=(x1p0，x2p0，…，xmp0)T，Yp0=(y1p0，y2p0，…，ysp0)T，

Xp=(x1p，x2p，…，xmp)T，YP=(y1p，y2p，…，ysp)T，

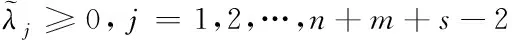
所以,如果Xp0≥Xp则有

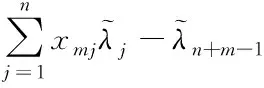
且至少有一类不等式严格成立.

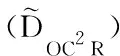
定理4 若决策单元p0为弱DEA有效(OC2R)，则其必为弱DEA有效(C2R)，反之不一定成立.

证明：若决策单元p0为弱DEA有效(OC2R)，则存在

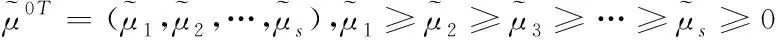
故满足模型(PC2R)中的约束条件

ωTXj-μTYj≥0(j=1，2，…，n)，ωTXp0=1,

下面通过实例应用的算例来说明当决策单元p0为弱DEA有效(C2R)，它不一定为弱DEA有效(OC2R)，如表3中的决策单元1，3，5，7.

定理5 设模型(POC2R)和(PC2R)的目标值为Vop和Vp，则满足Vop≤Vp(p=1，2，…，n).

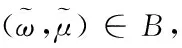
推论：若决策单元p0为DEA无效(C2R)，则其必为无效(OC2R)，反之不一定成立.

证明：若决策单元p0为DEA无效(C2R)，则存在最优解ω0，μ0，最优值Vp=μ0TYp0<1，故可利用上述定理5得Vop≤Vp=μ0TYp0<1可得决策单元p0为DEA无效(OC2R).

下面通过实例应用的算例来说明当决策单元p0为DEA无效(OC2R)时，有可能为DEA有效(C2R)，如表3中的决策单元1，3，5，8.

定理6 对模型(DOC2R)中一定存在决策单元p，其效率值为θ*=1，即必存在DEA弱有效决策单元.

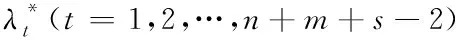
则有

由上述可得如下式子成立：

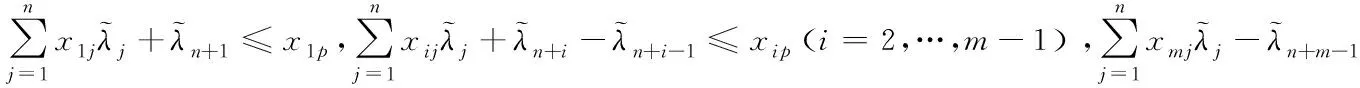
故由此可得模型(DOC2R)中一定存在弱有效决策单元.

2 实例应用

2.1 问题的描述

本文对八项技术创新成果进行相对效率评价，在选择评价指标时主要考虑以下因素：

(1)技术创新是一个周期性的技术经济过程，评价指标应全面、客观的反应其中的投入产出状况；

(2)技术创新的方向应与企业发展战略一致；

(3)创新成果在市场经济条件下更应重视其市场价值.

因此，这里从投入和产出角度选择了七项评价指标，并且投入指标中研究开发成本最重要，研究开发时间次之，依次递推；同样对于产出指标也是按重要程度从大到小排列并制定了相应的评判标准(满分5分，各标准的分数由左及右降低)，如表1所示.

表1 技术创新成果评价指标

2.2 问题模型的构建及求解

(1)数据的采集和处理

收集了八项技术创新成果，采用德尔菲法得出各项指标的具体数值，如表2所示.

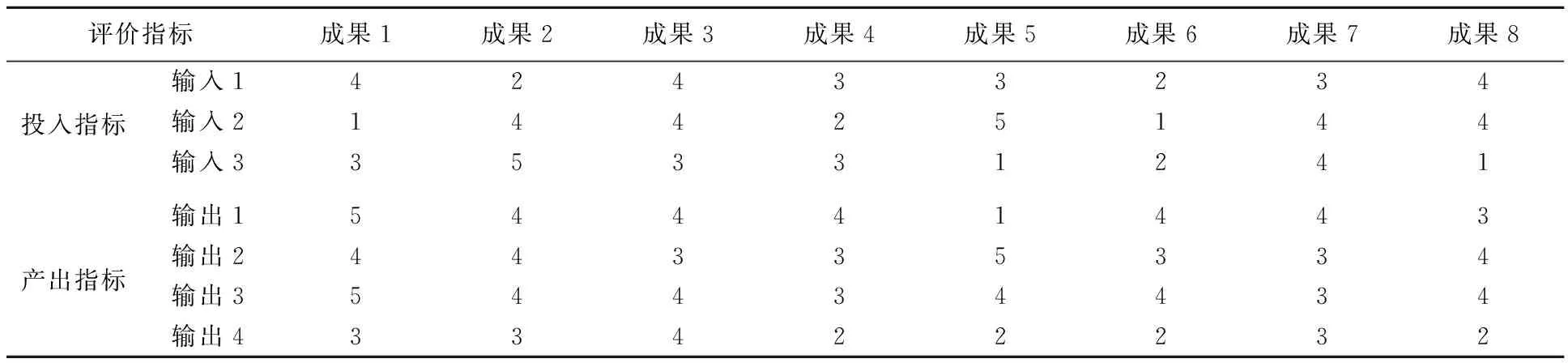
表2 技术创新成果评价指标数值

(2)评价结果

利用模型 (POC2R)和(PC2R)分别依次对上述八项技术成果进行评价，其相对效率值如表3所示.

表3 技术创新成果相对效率值

2.3 结果分析

从表3可以看出，利用C2R模型对8项技术创新成果进行评估，得到的评价结果并未反映出指标重要性的差异：如技术发明成果1，其中投入指标输入1是最重要的，但是其输入值最大，所以不可能为DEA有效；技术创新成果5，其输入指标2的输入值最大，并且它的重要性仅次于输入指标1；此外，其产出指标1的值最小，但是它是最重要的，所以技术创新成果5不可能为DEA有效.这些结果显然不符合客观实际.然而，运用指标偏好DEA模型对8项技术创新成果进行评价时，所得结果符合客观实际，符合决策者的要求.这从而可以证明指标偏好DEA模型的应用可以比较客观地反映每个指标的重要性的不同，限制了投入产出指标的权重，弥补了传统DEA对评价指标权重无限制的缺陷.

3 结 论

传统的DEA模型对指标权重没有任何限制，它实际上是选取对被评价的决策单位最有利的权重，并不能真实反映每个指标的重要性不同，因此其结果可能不符合客观实际.在此基础上构造了指标偏好DEA模型和对偶模型，从根本上解决了问题，使实际评估结果更加合理实用.