磁场对石墨烯中弱耦合极化子性质的影响

丁朝华， 裴志成， 赵 颖， 肖景林

(内蒙古民族大学 物理与电子信息学院， 内蒙古 通辽 028043)

1 引 言

石墨烯是一种新型材料，在光学、电学、力学和热学方面拥有很多优异的特性，具有良好的电子迁移率和生物相容性。石墨烯的电催化性能及其在生物器件方面有广泛的应用前景，可以被应用在液晶显示、超级电容器、太阳能电池和光子传感器等诸多方面。由于石墨烯的奇特性质和潜在的巨大应用前景，使其迅速成为凝聚态物理研究热点。近年来的一些实验揭示了石墨烯材料的光电和输运性质会受极化子效应的影响,而石墨烯中极化子性质受外部磁场和不同衬底材料的影响。Stauber等[1]应用LLP变分方法基于两次连续的幺正变换研究了石墨烯体系中载流子与体纵光学声子耦合的手征极化子的性质，同时在近期实验[2-5]中发现，在强磁场的作用下石墨烯中的朗道零能级的分裂(即能带的出现)导致异常的量子霍尔平台的出现，其中电子-声子相互作用导致的微小带隙的机制与实验数据是最接近的。Li和Wang等[6-7]采用变分法研究了磁场对石墨烯中强耦合形变势型极化子性质的影响，研究结果发现了这种极化子态导致的朗道零能级分裂。但到目前为止关于对石墨烯中弱耦合极化子性质研究的文献还很少见，本文作者[8-10]曾用线性组合算符和变分法研究了石墨烯中电子与表面声学声子(LA声子)强耦合下极化子性质的磁场效应问题，而且得出的结果与实验结果[11]相近。本文运用线性组合算符和Pekar变分法研究了电子与表面光学声子(SO声子)弱耦合下磁场对石墨烯中极化子性质的影响。

2 理论计算

取单层石墨烯的面为x,y平面，假设电子在石墨烯内运动，系统位于垂直于平面的均匀磁场(磁场强度为B)中，考虑到电子与表面光学声子(SO声子)相互作用，则该电子晶格耦合体系的哈密顿量为[12]：

(1)

对哈密顿量式(1)进行下列幺正变换[13]：

(2)

再对电子动量和坐标引入线性组合算符[14]：

(3)

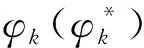
(4)

在有限低温的条件下，均匀磁场下体系的基态和第一激发态波函数可分别写为

(5)

(6)

式(4)的哈密顿量取体系基态式(5)和第一激发态式(6)的期待值，然后再利用对变分参量变分的变分法得到体系的基态和第一激发态能量分别为

E0=〈ψ0H′ψ0〉=

(7)

E1=〈ψ1H′ψ1〉=

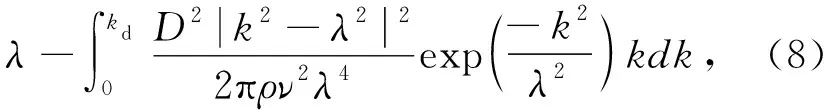
因此体系的结合能为

ΔE=E1±E0，

(9)

则体系极化子的跃迁频率为

(10)

3 结果与讨论

选用文献[15]的参数(VF=106m·s-1，ρ=7.5×10-7kg·m-2，ν=2×104m·s-1，D=50 eV)进行数值计算，来讨论电子与表面光学声子弱耦合情况下磁场对石墨烯中极化子的基态能量E0、第一激发态能量E1和跃迁频率ω的影响。数值计算结果如图1～6所示。

图1为德拜截止波数kd分别取1.5×108,2.0×108，3.0×108m-1时，电子与表面光学声子弱相互作用情况下石墨烯中极化子的基态能量E0随磁场强度B的变化关系。从图中可以观察出：极化子的基态能量E0随磁场强度B的变化曲线分裂为对称的两条，在磁场较弱时E0的绝对值是B的增函数，并逐渐趋于一个稳定的值，同时E0的绝对值也随kd的增加而增大。产生上述现象的原因如下：因为石墨烯所特有的线性狄拉克能带结构，使能级在n=0这个轨道位置具有一个性质，即在磁场作用下，当费米能级位于n=0这个轨道能级的右侧时，n=0的朗道能级变成电子与空穴的共享轨道，二者又因为Lorenz效应分别与体系的声子相互作用，引起相互作用能的绝对值相等但正负相反。

图2表示当磁场强度B分别为10，20，30 T时，石墨烯中弱耦合极化子的基态能量E0与德拜截止波数kd的关系曲线，由图中可以看出：在磁场B影响下，E0随kd的变化曲线也分裂成对称的两条，E0的绝对值是德拜截止波数kd的增函数，最后趋于一个稳定的值保持不变，这个结果与实验[16]结果符合。

图1 E0随B的变化曲线

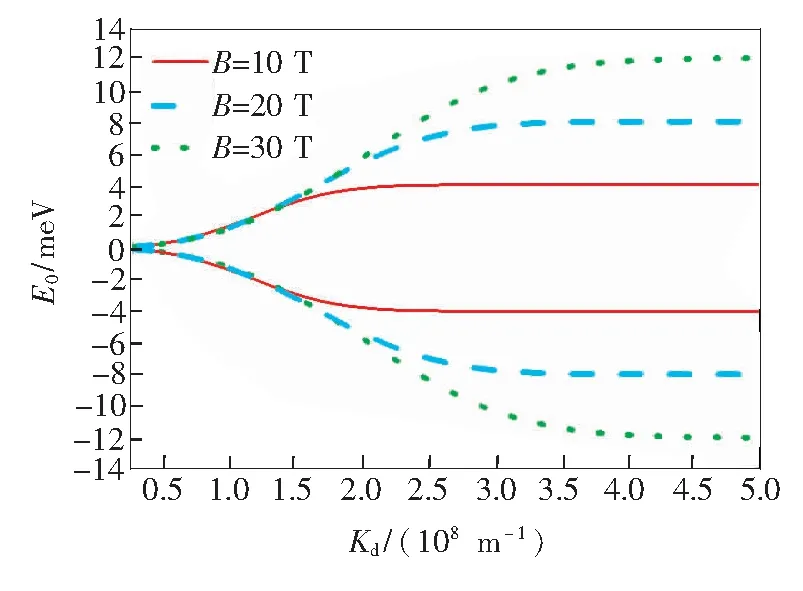
图2 E0随kd的变化曲线

图3反映了德拜截止波数kd取不同值时石墨烯中弱耦合极化子的第一激发态能量E1随磁场强度B的变化曲线，由图3可知第一激发态能量E1随着磁场强度B的增强而增大。

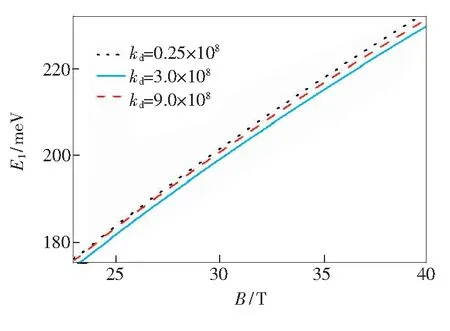
图3 E1随B的变化曲线

图4为磁场强度分别取B=10，20，30 T的情况下石墨烯中弱耦合极化子的第一激发态能量E1随德拜截止波数kd变化的依赖关系。由图可见，磁场较大时(图4中磁场强度稍大的两条曲线)，极化子的第一激发态能量E1都是随德拜截止波数kd的增加而增大，最后会达到一个稳定的值；而磁场较弱时德拜截止波数kd对第一激发态能量E1的影响较弱。这是因为石墨烯材料中的自旋和轨道之间存在相互作用，并且自旋的影响会与磁场的强弱有关：磁场越强时，自旋的影响越强，E1随kd的变化很明显；而磁场较弱时，自旋的影响也越弱，E1几乎不随德拜截止波数kd的变化而变化。

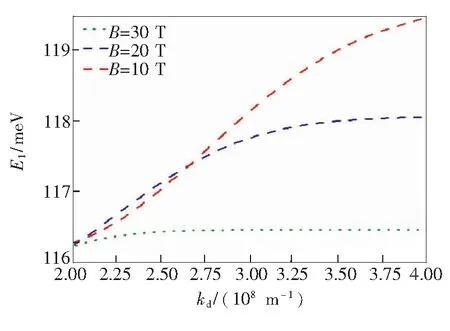
图4 E1随kd的变化曲线

图5给出了在考虑电子与表面光学声子弱耦合情况下石墨烯中极化子的跃迁频率ω在德拜截止波数kd取不同值时与磁场强度B之间的依赖关系。从图5可以看出，弱耦合极化子的跃迁频率是磁场强度的增函数。

图5 ω随B的变化曲线

图6反映了在考虑电子与表面光学声子弱耦合情况下石墨烯中极化子的跃迁频率ω在磁场强度B取不同值时与德拜截止波数kd之间的依赖关系。从图中可以观察出：当磁场稍强时，跃迁频率ω会随着德拜截止波数kd的增大先逐渐加快，然后会达到一个稳定的值。而当磁场稍弱时，跃迁频率ω先随德拜截止波数kd的增大而增强并达到最大值，然后变成德拜截止波数的减函数，最后也趋于一个稳定的值。原因与图4的相同。

图6 ω随kd的变化曲线

4 结 论

在考虑电子与表面光学声子(SO声子)弱耦合情况下，本文采用线性组合算符和Pekar变分法研究了磁场对石墨烯中极化子的基态能量E0、第一激发态能量E1和跃迁频率ω的影响。数值计算结果表明，在德拜截止波数kd取定值时，弱耦合极化子基态能量E0随磁场强度B变化的曲线会分裂成对称的两条；极化子的第一激发态能量E1和跃迁频率ω均随磁场B的增强而增加，并且E1和ω随磁场强度B变化的曲线也不会分裂。磁场强度B取定值时，基态能量E0随德拜截止波数kd的变化曲线也会分裂成对称的两条，基态能量E0的绝对值是德拜截止波数kd的增函数，直到达到一个稳定的值；弱耦合极化子的第一激发态能量E1和跃迁频率ω都是德拜截止波数kd的增函数，最后趋于一个稳定的值。