钢混厂房结构多层次模拟与疲劳损伤累积的循环块更新算法*

吴佰建 唐一萌 李兆霞

(1.东南大学土木工程学院，南京 210096;2.东南大学，江苏省工程力学分析重点实验室，南京 210096)

改革开放以来，我国建成的房屋建筑物面积不断快速增长，其中工业建筑物约占1/4，数量极其巨大。根据原冶金工业部建筑研究总院对1990—2007年间的17例钢铁厂房倒塌事故的统计研究［1］发现，因结构耐久性破坏倒塌有9例，占52.9%。随着20世纪建造的一大批钢混工业厂房的服役年限达到了设计寿命，目前对于工业建筑结构疲劳问题的研究逐渐成为工程界关注的热点问题，其中除了疲劳强度和疲劳寿命外，结构的疲劳损伤演化也成为了关心的问题之一。

对于混凝土的疲劳损伤演化问题，不少学者得出了较为丰厚的理论成果［2-5］。最早在工程中得到广泛应用的疲劳累积损伤理论是1945年Miner提出的线性累积损伤理论［2］，即 Miner准则。随后一些学者在试验的基础上提出了对Miner线性累积模型准则进行修正的模型或基于损伤演变规律建立了非线性累积损伤模型［6-9］，例如指数型累积损伤模型、双曲线型累积损伤模型、三次多项式型累积损伤模型、修正线性累积损伤模型等。然而其中很多是基于试验对材料损伤演化的经验曲线进行探究，缺乏理论依据的支持。在这方面，李兆霞根据高周疲劳损伤演化的基本方程，并在分析大跨桥梁结构中疲劳应力特征的基础上建立了钢桥梁结构在服役荷载下的高周疲劳损伤力学模型［10］。

本文根据高周疲劳损伤演化的基本方程，推导出适用于混凝土材料的疲劳损伤演化规律，并在考虑循环块更新的情况下，通过多层次数值仿真模型得到钢混厂房疲劳损伤演化模拟结果。

1 混凝土疲劳损伤演化律

1.1 基于连续损伤力学的疲劳损伤累积规律

根据连续损伤力学理论，高周疲劳的损伤演化基本方程可以写为［10］：

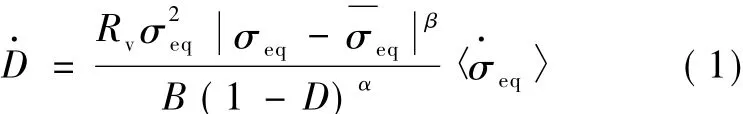
其中 Rv=(σ*/σf)2

式中：B、α、β为材料常数;σf为疲劳应力极限;σeq为多轴受力状态下的等效应力，对于金属材料为von Mises应力;σ*为损伤等效应力，在塑性阶段即为von Mises应力;Rv为一个代表三向应力状态比值影响的函数;σeq为平均有效正应力。

首先忽略平均有效应力的影响，考虑 σeq=σm=0(σm为平均主应力)，并忽略(1－D)α的变化，将式(1)在一个循环内两边积分，可得［10］：式中：N为吊车荷载的循环次数;σM为本次循环的最大应力。

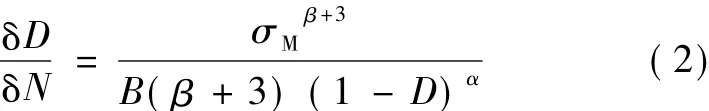
进一步考虑平均应力的影响：

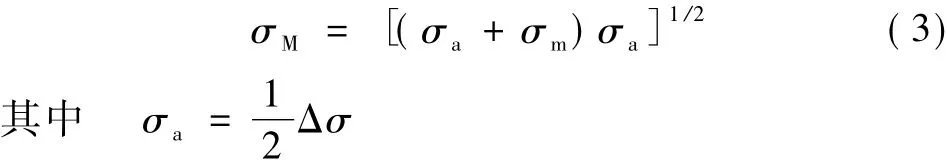
式中：Δσ为应力幅。

将式(3)代入式(2)中，可得：

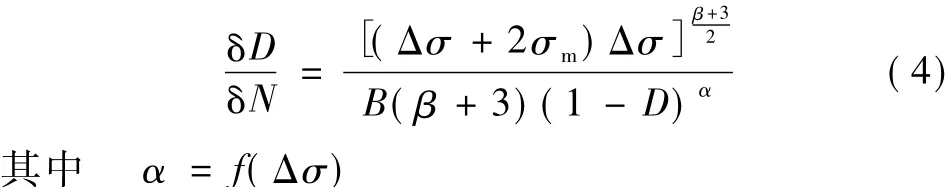
为了反映混凝土材料的拉、压异性，可将应力张量进行分解［11］，得到受拉应力张量 σ+和受压应力张量 σ－：式中：分别为受拉有效应力张量、受压有效应力张量;pi为主方向的单位向量。

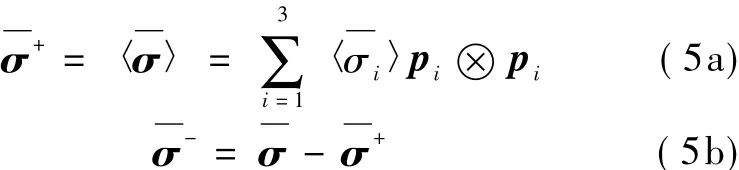
同样考虑到混凝土拉、压特性不同，将式(4)按受拉和受压分解，可得：

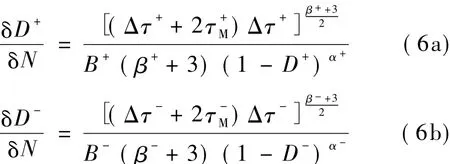
式中：+、-分别表示受拉和受压;τM表示混凝土的等效应力最大值。参考文献［11］，将混凝土受拉和受压等效应力定义如下：

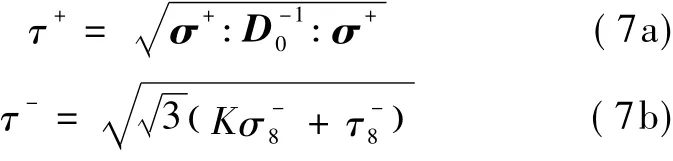
式中：τ+、τ－分别表示混凝土受拉部分和受压部分的等效应力;、分别为受压应力张量σ－的八面体正应力和八面体剪应力;K为材料参数。

一个循环块产生的总疲劳损伤率可表示为：

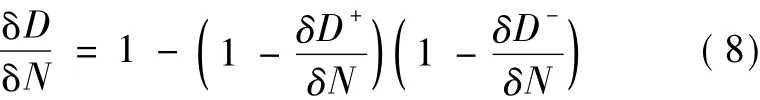
由于吊车荷载作用下吊车梁主要呈现受弯疲劳，忽略受压损伤D－，则式(8)可简化为：

式(9)即为适用于钢混厂房关键构件的疲劳损伤累积规律，具体形式由式(6a)给出。

上述得到的疲劳损伤累积方法考虑了钢混厂房的材料特性和荷载规律，对高周疲劳损伤演化方程进行了适当的简化，提高了计算的成本和效率。

1.2 混凝土疲劳损伤律的材料参数确定

钢混厂房的疲劳损伤律中的参数B+、α+、β++3需要通过混凝土受弯疲劳试验确定，通过在不同应力水平下的纯弯试验得到的残余强度的结果［12］，可以转化为材料的疲劳损伤累积曲线，见图1a。

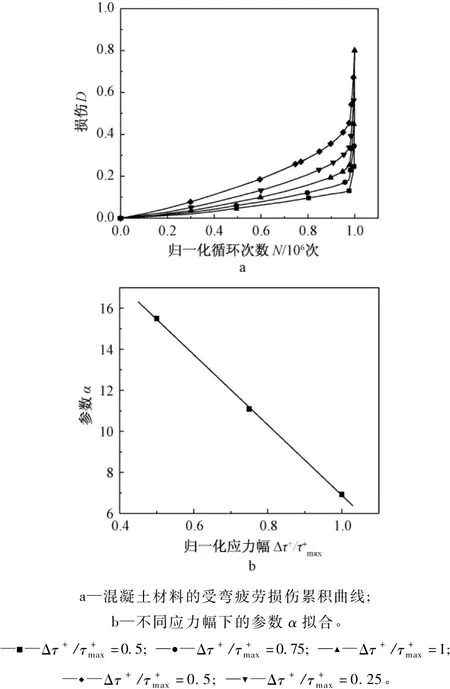
图1 参数拟合数据Fig.1 Data for parameter fitting

确定参数的步骤如下：首先确定α+的取值。由于α+=f(Δτ+)，α+的取值与应力幅有关。在曲线上取两点可得到α+的值，由图1b可知，不同的应力幅水平下的α+值有以下线性关系：

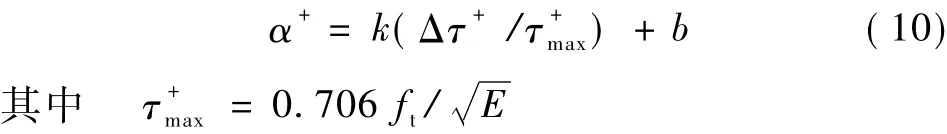
式中：Δτ+/为归一化的有效应力幅;ft为混凝土抗拉强度。

在已知α+的情况下，取不同曲线上的两点，可求出β++3的取值，然后代入式(6a)可以求出B+的值。各参数的取值如表1所示。

表1 疲劳损伤律中的参数拟合值Table 1 Results of damage parameter fitting

2 钢混厂房结构多层次数值模拟

根据某车间钢混厂房的现场检测结果，对钢混厂房的构件进行初步整理，忽略抗风柱、外墙等结构次要构件，重点考虑梁、柱、柱间支撑等主要结构构件。选取一个8榀的单层单跨混凝土厂房结构建立整体梁单元模型，该结构的具体尺寸如图2所示。

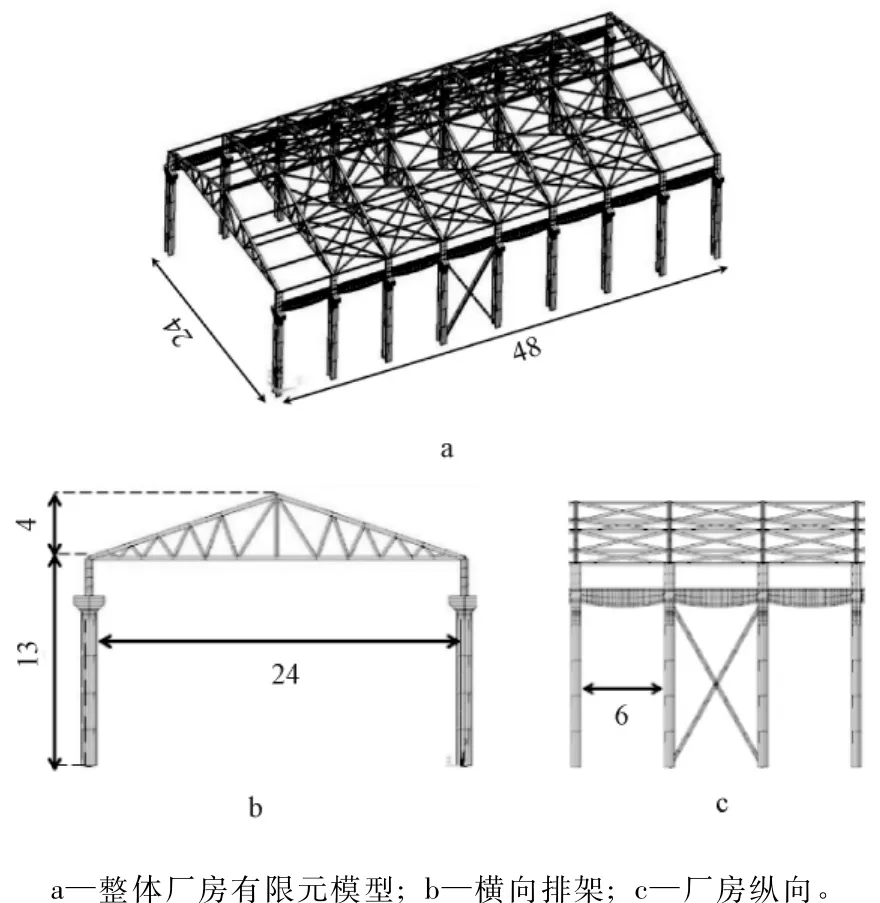
图2 根据实际厂房结构建立的整体数值模型 mFig.2 Numerical model of the industriel building

该厂房的吊车起吊量为100 kN，参考大连起重机器厂50～500/100 kN吊钩桥式起重机技术规格［13］，可得吊车车轮额定最大轮压为136 kN。考虑吊车梁上竖直吊车荷载为额定最大轮压的最不利工况，利用影响线方法得到各构件危险截面的应力时程如图3所示。

根据得到的应力时程和现场检测结果的损伤信息，可以得出以下结论：在各混凝土构件中，吊车梁端部截面、梁跨中截面的应力水平和应力幅最大，其次是上柱底截面和下柱底部截面。考虑到吊车梁是直接承受吊车荷载的构件，端部和跨中截面是弯矩较大的区域，它们的应力水平和应力幅自然最大;而上柱底截面和牛腿顶部截面存在突变，由于应力集中效应，较为薄弱的上柱底截面的应力水平就比较高。

综上分析，吊车梁端部截面、梁跨中截面和上柱底截面是整体结构的危险部位，即吊车梁和牛腿组成的局部是钢混厂房的关键构件。

选取结构的纵向一跨进行分析，建立吊车梁与牛腿节点的模型。该局部模型等效简化成3个部分，如表2所示。关键构件的数值仿真模型如图4所示。

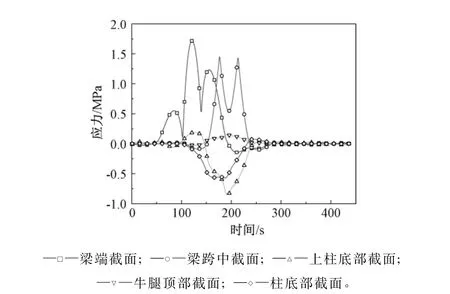
图3 各混凝土构件危险截面的应力时程曲线Fig.3 Stress history on critical cross-sections for all concrete components

表2 局部模型的等效简化方法Table 2 Equivalence and simplification of local-level simulation model

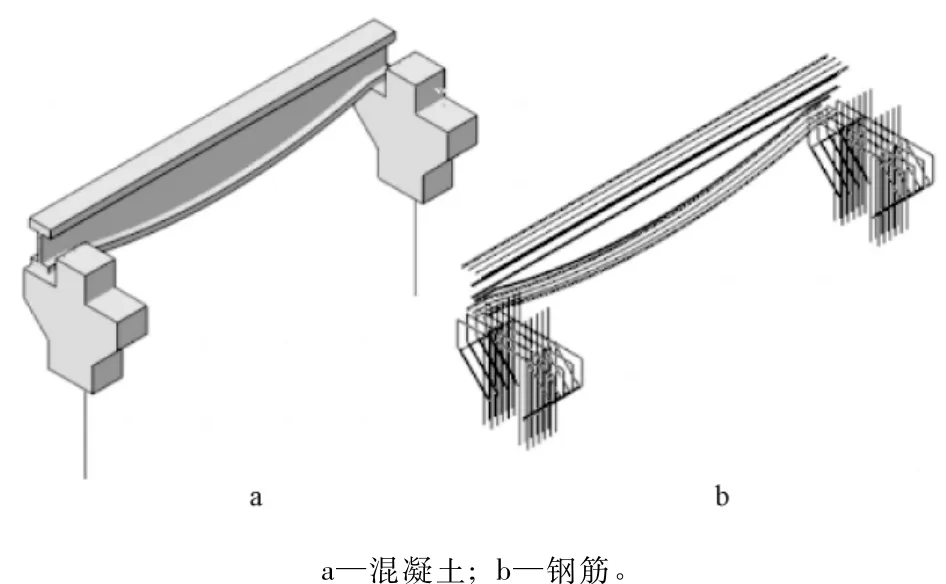
图4 关键构件的数值仿真模型Fig.4 Numerical model of key components

3 混凝土疲劳损伤累积过程的循环块更新算法

传统的疲劳分析方法一般为：首先确定一个标准应力循环块，在这个循环块中损伤和应力状态是不变的，并且只在每一个循环块结束时更新损伤值，以循环块的不断重复来模拟损伤的累积。传统方法的优点在于计算步骤简单，只需进行一次弹性计算，得到应力谱即可模拟疲劳损伤的累积过程。但是这种方法的弊端在于没有进行循环块的应力幅更新，对于钢筋混凝土结构疲劳过程中的应力重分布没有很好的体现。

为弥补传统方法的不足，考虑循环块循环过程中的应力幅更新，可以更为准确地反映结构的损伤劣化过程，流程如图5所示。具体的计算步骤如下：

1)在上一节得到的关键构件局部模型基础上进行一次弹性加载，记录每一个积分点的最大等效拉应力;

2)假设忽略材料的自重，即不计吊车荷载作用下结构的最小应力，并且在吊车运行一周过程中只有一次加卸载循环，即只有一个峰值应力，则平均等效拉应力=/2。则疲劳损伤率的算式(6a)可简化为：

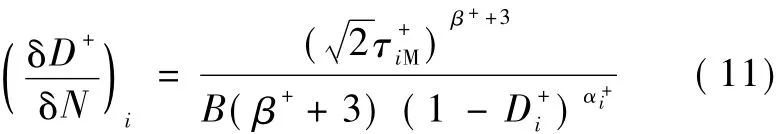
式中：下标i表示循环块的更新次数。由疲劳损伤累积率式(11)，可计算得到一次循环后得到的疲劳损伤 δ。

3)根据疲劳发展一般为前期缓慢，后期临近疲劳失效时快速发展的特点，可以人为控制循环块内的荷载循环次数ΔNi，以提高计算效率。这里取第一个循环块的循环次数ΔN1为0.9×106次(假设全年吊车来回移动3万次，则ΔN1=0.9×106次代表结构服役 0.9×106/(3 ×105)=30 a)，其后的 ΔNi均取0.3×106次(代表结构服役10 a)。

4)假设循环块内的损伤线性增加、应力幅不变，有以下疲劳损伤快速累积规律：

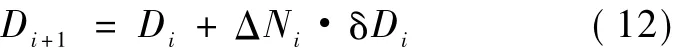
由式(12)更新的损伤值可用于下一次弹性加载计算的刚度折减，循环块的应力计算式如下：

式中：σi+1、εi+1分别为第i+1次吊车移动加载下的应力张量和应变张量;E为材料弹性模量。

考虑到钢混结构的高周疲劳一般以钢筋的疲劳断裂为破坏标志，则根据跨中底部混凝土的损伤状态进行疲劳破坏判断：当跨中底部混凝土尚未达到破坏强度时，重新按照步骤1)—步骤4)进行下一步的损伤累积和循环块更新;当跨中底部混凝土全部已经达到破坏强度时，停止循环，将当前的累积循环次数作为疲劳寿命。

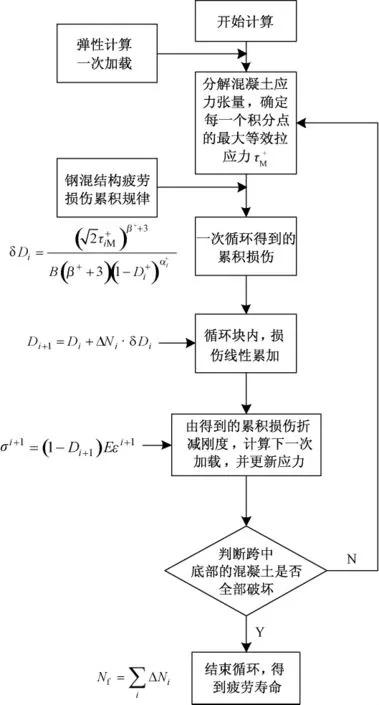
图5 钢混厂房关键构件疲劳损伤分析流程Fig.5 Flow chart of key component fatigue analysis for concrete industrial buildings

4 钢混厂房关键构件的疲劳损伤演化过程分析

由于吊车荷载的欠载效应、小车移动等原因，实际的吊车轮压小于额定最大轮压。根据文献［14］统计的吊车荷载服从极值 I型概率分布，其轮压的均值为66.64 kN。考虑到荷载的动态效应，将轮压乘以动力系数1.06，可得动力荷载为70.638 4 kN。

利用第3节中的疲劳损伤分析流程，分析含已有缺陷的关键构件疲劳损伤的演化过程，以及结构的疲劳性能衰退情况，如图6、图7所示。

由图6可知，混凝土的疲劳损伤大部分出现在梁底跨中区域，并且随着服役年限的增加，向梁底两边以及腹板蔓延。

当服役年限在30～40 a时，关键构件中单元的最大损伤值尚未超过0.3，可见之前的疲劳损伤演化是极其缓慢的;40～60 a，疲劳损伤迅速累积，吊车梁跨中底部开始有部分单元的疲劳损伤达到了损伤极限值;60～70 a，吊车梁底部大部分单元的疲劳损伤都达到了极限值，并且在70年之后，吊车梁底部的混凝土单元疲劳损伤全部达到了极限值，表示关键构件已经丧失了承载能力。GB 50068—2001《建筑结构可靠度设计统一标准》中钢混厂房的设计基准年限一般为50年，相比之下是较为保守的。

图6 钢混厂房关键构件的疲劳损伤演化云图Fig.6 Damage contour and its evolution in key components of the reinforced concrete industrial building

如图7所示，随着服役年限的增加，钢筋应力和梁跨中挠度不断增加，并且增加速率呈现出逐渐变大的趋势。特别是在40～60 a之间，即跨中底部混凝土快速进入损伤极限状态时，增长幅度最大。

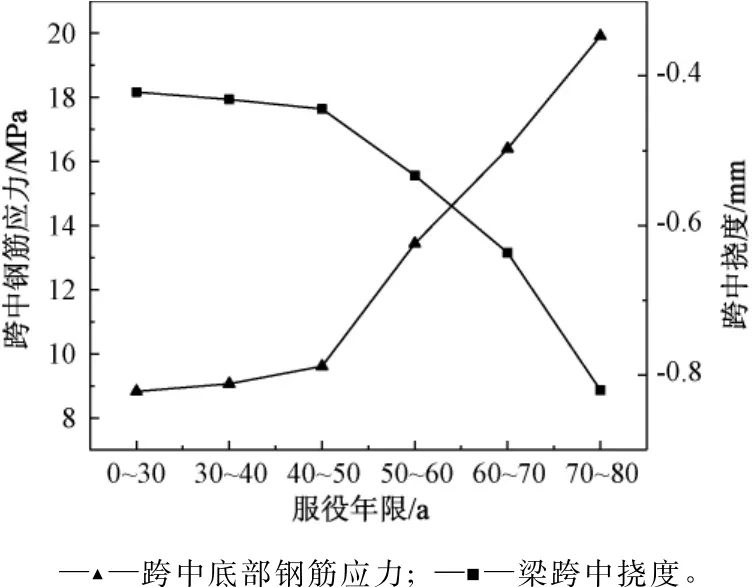
图7 跨中底部的钢筋应力和挠度变化Fig.7 Changes of mid-span displacement and steel bar stress during service life of the building

5 结束语

本文基于连续损伤力学的高周疲劳演化基本方程，推导出了适用于混凝土材料的损伤累积公式。随后考虑循环块应力幅更新的影响，并通过钢混厂房的多层次数值仿真模型实现了结构疲劳损伤演化过程的模拟。结果表明，考虑循环块更新的混凝土材料疲劳分析方法可以模拟钢混结构的疲劳损伤演化以及疲劳性能的劣化过程。

模拟结果表明：钢混厂房关键构件的损伤分布不是均匀的，而是局部集中的，且大部分出现在梁底跨中区域;结构的损伤演化和疲劳性能劣化过程体现出了疲劳损伤的非线性演化特性，即疲劳初期损伤发展缓慢，后期迅速累积;计算得到的疲劳寿命比结构设计基准期长，说明相关标准的规定是相对保守的。