解锐角三角函数易错题分析

文 /武乾俊

锐角三角函数是各地中考的必考内容，现把锐角三角函数中的易错题列举出来，供你学习时参考．

一、锐角三角函数的概念不清

例1 如图1，两根竹竿AB和AD斜靠在墙CE上，量得∠ABC=α，∠ADC=β，则竹竿AB与AD的长度之比为（ ）.

错因诊断：对边与斜边的比值是这个角的正弦．

图1

二、在直角三角形中，误认为∠C一定是直角

例 2在Rt△ABC中，∠A=90°，，AC=6，则AB=（ ）.

A.4 B.6 C.8 D.10

错因诊断：因为∠A=90°，所以BC为斜边，∠C的对边AB是直角边.

正解：在Rt△ABC中，

三、没有掌握三角函数的增减性

例3若锐角α满足且，则α的范围是（ ）.

A．30°＜α＜45° B.45°＜α＜60°

C．60°＜α＜90° D.30°＜α＜60°

∴30°＜α＜45°.选A．

错因诊断：当α为锐角时，正弦和正切值随着角度的增大而增大，而余弦值随着角度的增大而减小．

四、在非直角三角形中利用锐角三角函数求值

例 4在▱ABCD中，对角线AC，BD相交于点O，若AB=4，BD=10，sin∠BDC=，则▱ABCD的面积是＿＿＿ ．

错解：由▱ABCD中BD=10，可知OD=5.

图2

错因诊断：锐角三角函数是在直角三角形中定义的，△OCD不是直角三角形，因此锐角三角函数的边角关系不成立.把∠BDC放在直角三角形中，才能利用锐角三角函数的知识来求解.

正解：如图2，过点C作CE⊥BD于点E.

五、忽视三角函数值的取值范围

例5已知锐角A满足关系式2sin2A-7sinA+3=0，则sinA的值为＿＿＿ ．

错解：由2sin2A-7sinA+3=0，即（sinA-3）（2sinA-1）=0．

∴sinA-3=0或2sinA-1＝0，即sinA=3或．

错因诊断：A为锐角，则0＜sinA＜1，0＜cosA＜1，因此sinA=3应舍去，只有一个值sinA=．（正解略）

六、思考问题不全面而漏解

例 6△ABC中，AB=12，AC=，∠B=30°，则△ABC的面积是＿＿＿ ．

错解：如图3，作AD⊥BC，垂足为点D.

在Rt△ABD中，∵AB=12，∠B=30°，

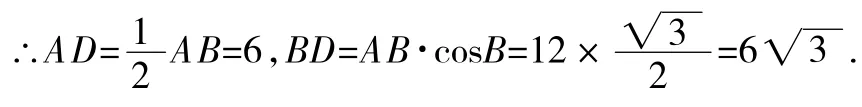
错因诊断：△ABC不一定是锐角三角形，高AD不一定在△ABC的内部，应分高AD在△ABC内部和在△ABC外部讨论.

正解：（1）若高AD在△ABC的内部，如图3，解法同上；

（2）若高AD在△ABC的外部，如图4，作AD⊥BC交BC延长线于点D，

图3

图4

七、取近似值不当

例7如图5，为了测量建筑物AB的高度，在D处树立标杆CD，标杆的高是2m，在DB上选取观测点E，F，从E处测得标杆和建筑物的顶部C，A的仰角分别为58°，45°，从F处测得C，A的仰角分别为22°，70°．求建筑物AB的高度（精确到0.1m）．（参考数据：tan22°≈0.40，tan58°≈1.60，tan70°≈2.75）

图5

错解：在Rt△CED中，∠CED=58°，

在Rt△CFD中，∠CFD=22°，

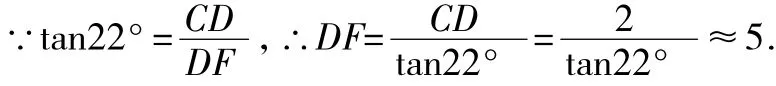
∴EF=DF-DE=3.7.

∴EF=BE-BF=AB-0.4AB=0.6AB，

∴0.6AB=3.7，解得AB=6.2（m）.

错因诊断：在取近似值时，没有按题目的要求先多取一位，也没有到最后再按要求取近似值，导致结果有较大的误差.

正解：在Rt△CED中，∠CED=58°，

∴EF=BE-BF=AB-0.36AB=0.64AB，∴0.64AB=3.75，解得AB≈5.9（m）.因此，建筑物AB的高度约为5.9m.