解 直角三角形的应用
文 /刘雅菲 扶泽妃
解直角三角形在测量、航空、航海、工程等方面的应用广泛.下面把解直角三角形的应用类型归纳如下,供你学习时参考.
一、仰角、俯角问题
例1如图1,两座建筑物的水平距离BC为60m,从C点测得A点的仰角α为53°,从A点测得D点的俯角β为37°.求两座建筑物的高度(参考数据.
解:过点D作DE⊥AB于E,
则DE=BC=60m.
在Rt△ABC中,


图1
∴AB=80(m).
在Rt△ADE中,

∴AE=45(m),
∴BE=CD=AB-AE=35(m).
答:两座建筑物的高度分别为80m和35m.
点评:仰角是向上看的视线与水平线的夹角,俯角是向下看的视线与水平线的夹角.解决测量建筑物的高度问题要了解角与角之间的关系,找到与已知和未知线段相关联的直角三角形.当图形中没有直角三角形时,要通过作高或垂线构造直角三角形,在直角三角形中应用三角函数的定义求解.
二、方位角问题
例2某区域平面示意图如图2,点O在河的一侧,AC和BC表示两条互相垂直的公路.甲勘测员在A处测得点O位于北偏东45°,乙勘测员在B处测得点O位于南偏西73.7°,测得AC=840m,BC=500m.请求出点O到BC的距离.
解:作OM⊥BC于M,ON⊥AC于N,
则四边形ONCM为矩形,
∴ON=MC,OM=NC.
设OM=x,则NC=x,AN=840-x,
在Rt△ANO中,∠OAN=45°,
∴ON=AN=840-x,
则MC=ON=840-x.
在Rt△BOM中,
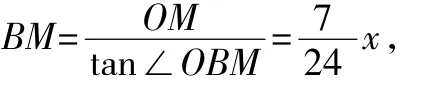
∵BM+MC=BC,


图2
解得x=480.
答:点O到BC的距离为480m.
点评:在解决有关方向角的问题中,有时所给的方向角并不一定在直角三角形中,需要利用两直线平行或余角的性质求出直角三角形的角度,利用三角函数的定义求解.
三、坡比问题
例3日照间距系数反映了房屋日照情况.如图3,当前后房屋都朝向正南时,日照间距系数=L:(H-H1),其中L为楼间水平距离,H为南侧楼房高度,H1为北侧楼房底层窗台至地面高度.

图3
如图4,山坡EF朝北,EF长为15m,坡度为i=1∶0.75,山坡顶部平地EM上有一高为22.5m的楼房AB,底部A到E点的距离为4m.
(1)求山坡EF的水平宽度FG;
(2)欲在AB楼正北侧山脚的平地FN上建一楼房CD,已知该楼底层窗台P处至地面C处的高度为0.9m,要使该楼的日照间距系数不低于1.25,底部C距F处至少多远?
解:(1)在Rt△EFG中,
∵∠G=90°,
设EG=4x,则FG=3x,
∵EF=15,
∴5x=15,x=3,
∴FG=3x=9.
即山坡EF的水平宽度FG为9m.
(2)∵L=CF+FG+EA=CF+9+4=CF+13,
EG=4x=12,
H=AB+EG=22.5+12=34.5,H1=0.9,
∴ 日照间距系数=L:(H-H1)=,
∵该楼的日照间距系数不低于1.25,

∴CF≥29.
答:要使该楼的日照间距系数不低于1.25,底部C距F处至少29m远.
点评:坡度是坡面的铅直高度h和水平宽度l的比,又叫做坡比.它是一个比值,体现了斜坡的陡峭程度,一般用i表示,常写成i=1:m的形式.正确将坡比转化为直角三形中两条直角边的比是解这类问题的关键.
四、其他问题
例4如图5,窗框和窗扇用“滑块铰链”连接,图7是图6中“滑块铰链”的平面示意图,滑轨MN安装在窗框上,托悬臂DE安装在窗扇上,交点A处装有滑块,滑块可以左右滑动,支点B,C,D始终在一直线上,延长DE交MN于点F.已知AC=DE=20cm,AE=CD=10cm,BD=40cm.
(1)窗扇完全打开,张角∠CAB=85°,求此时窗扇与窗框的夹角∠DFB的度数;
(2)窗扇部分打开,张角∠CAB=60°,求此时点A,B之间的距离(精确到0.1cm).

图5

图6

图7
解:(1)∵AC=DE=20cm,AE=CD=10cm,
∴四边形ACDE是平行四边形,
∴ AC∥DE,
∴∠DFB=∠CAB,
∵∠CAB=85°,
∴∠DFB=85°.
(2)如图7,作CG⊥AB于点G,
∵AC=20,∠CGA=90°,∠CAB=60°,
∵BD=40,CD=10,
∴CB=30,
∵BG2=BC2-CG2,

即A,B之间的距离为34.5cm.
点评:解实际问题的思考方法是:①将实际问题抽象为数学问题(画出平面图形,构造出直角三角形,把实际问题转化为解直角三角形的问题,本题给出了平面图形);②根据题目已知条件选用适当锐角三角函数或边角关系去解直角三角形,得到数学问题的答案,从而得到实际问题的答案.

