无线光通信系统中极化码编译码技术
安 琪,毛忠阳,谢洪森,胡 昊
(1.海军航空大学,山东烟台264001;2.海军航空大学青岛校区,山东青岛266041)
无线光通信(Free Space Optical,FSO)技术是以激光束为信息载体在大气中传递信息的通信手段,它结合了无线电通信与光纤通信的优点,具有保密性好、传输速度快、无须频谱许可、安装灵活、成本低廉等优点[1-3]。因此,广泛应用于光纤通信备份、应急通信、战场保密通信、灾后通信恢复、实时超高清视频传输、量子密钥分发等领域,也已成为解决宽带网络“最后一公里”传输瓶颈的有效途径。
然而,大气信道衰减效应和湍流效应的存在,极大地降低了FSO通信系统的可靠性和稳定性[4]。为了解决由大气湍流而导致光信号在传输中产生光强起伏,进而影响系统误码性能的问题,信道编码技术被引入无线光通信系统中。
无线光通信系统中纠错编码技术研究主要集中在对RS码、LDPC码和Turbo码的研究。在文献[5]中,RS(15,9)码被应用于无线光通信系统中,相较于未编码系统,引入RS码的无线光通信系统在AWGN信道下可以获得误码性能2个数量级的改善;RS码的不足之处在于解码过程中不使用软信息,限制了编码增益提高。在文献[6]中,Turbo码被应用于无线光通信系统中,在光强闪烁强烈的条件下,相较于未编码系统,引入Turbo码的无线光通信系统在相同误码率情况下,可以获得约9dB的编码增益;然而,Turbo码的译码设备很复杂,工程实现有很大难度,译码时延太大,无法应用于实时的通信系统,存在误码率底线。LDPC码在一定程度上克服了Turbo码的缺点,不存在误码率底线,其译码本质为并行算法,因而译码时延较短[7-8];然而,LDPC码存在译码复杂度高的问题,译码复杂度的降低,通常要以牺牲误码性能优势为代价[9]。因此,构造出具有较低复杂度的编译码方式并验证其具有无限接近信道容量最大值的特性,成为一个难以达到但又十分诱人的目标。
2009年,Erdal Arikan提出极化码(Polar code)[10],以其能被严格证明“达到”信道容量的性质,并于2016年确定5G控制信道eMBB(增强移动宽带)场景的编码方案。围绕着极化码的编译码方法及应用也吸引众多学者的关注[11-12],Deng Hui等从信息论的角度在衰落信道下对极化码展开研究,对信噪比进行筛选,证明了极化码在衰落信道下也可以对信道的误码性能有明显的改善作用[13]。Lanying Zhao在分析了嘈杂布莱克威尔信道下的极化码编译码应用[14]。Keita Ito等分析了极化码在卫星激光中的应用[15]。
本文针对大气湍流导致光信号在传输中产生光强起伏,进而降低系统误码性能的问题,将Polar编译码技术引入无线光通信系统中。在分析无线光通信系统及大气湍流信道模型的基础上,重点对大气湍流信道下Polar码编译码改进方案展开了研究,通过对比未编码系统,验证了Polar码在大气湍流信道下对无线光通信系统可靠性的改善,并仿真分析了不同码长、码率对Polar码编码增益的影响。
1 无线光通信系统模型
1.1 无线光通信系统
FSO通信系统通常由发射部分、接收部分以及大气信道组成。发射部分主要由信道编码、信源编码、调制、光信号放大以及发射天线等组成;接收机主要由光接收天线、光电监测器和电信号处理器等组成;信道为大气信道,在光通信的过程中极大的受到大气湍流及复杂气象的条件的影响。无线光通信模型如图1所示。
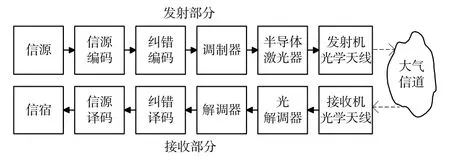
图1 无线光通信模型Fig.1 FSO communication model
1.2 大气信道模型
FSO通信的传输媒质为大气,大气对通信系统性能的影响主要由大气衰减作用和大气湍流效应造成。大气衰减作用是指大气信道中的气体分子和各种悬浮的微粒,如尘、水、气溶胶等对激光束的和散射作用引起激光光束能量衰减的现象。大气湍流效应由大气密度不均匀引起,随机产生的复杂多变的气候现象会导致大气温度及压力不均匀进而引起大气密度发生明显不均匀,大气折射率起伏,最终造成激光束的闪烁、分裂、弯曲、扩展以及空间相干性降低[16]。
在弱湍流的信道条件下,通常采用对数正态分布模型得到接收端光强I的概率密度函数[17]:

式(1)中:I为大气湍流的强度;σ2为湍流强度对数方差,在弱湍流的条件下σ2<0.3。
2 极化码编译码方法
极化码编码技术的实现建立在信道极化现象之上。信道极化是由N个相互独立的二进制离散无记忆信道(Binary Discrete Memoryless Channel,BDMC)W过多次结合与拆分,得到另一组由N个独立信道组成的信道的操作,这个操作体现了极化的影响,随着N的增大,除了指数i消失的那部分,对称容量对于所有指数i都趋向于0或者1。
2.1 信道极化现象
极化码编码过程采用递推的方式将给定的BDMCW的样本结合成一个向量信道WN:XN→YN,N可以为2的任意整数次幂,N=2n,n≥0。递推运算开始于第0层(n=0)只有一个信道样本W,设W1=W。第1层递推由2个独立的W1组成,得到信道W2:X2→Y2和转移概率为
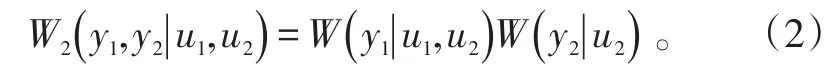

图2 信道W2Fig.2 ChannelW2
图3为下一层递推,2个独立的W2信道样本结合产生信道W4:X4→Y4,信道转移概率为

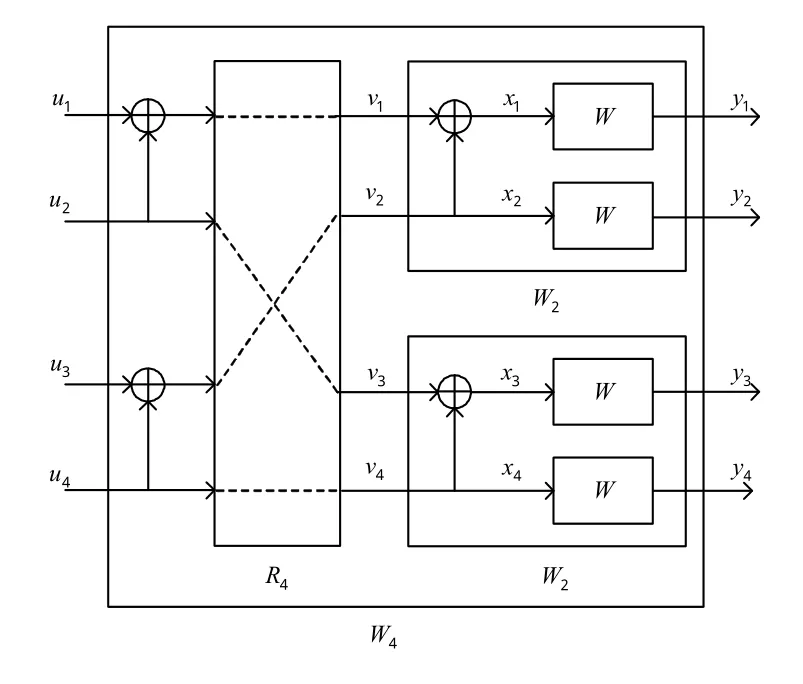
图3 信道W4及它与W2和W的关系Fig.3 ChannelW4and its relation toW2andW
图3中,R4是将一组输入映射到的转置运算。从输入W4到输入W4的映射可以写成,其中,G4可表示为

由此,可以得到W4和W4的转移概率关系为。
图4表现了递推算法的通式,2个独立的WN2结合产生WN。向量到WN时首先转化成,因而有。
图4中,RN是一个逆移位运算,它的作用是将输入的转化成,并作为图中2个WN2的输入。

图4 由WN2得到WN的递推构造过程Fig.4 Recursive construction ofWNfromWN2
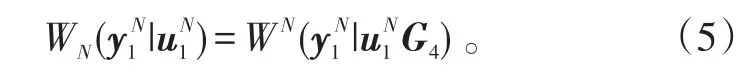
由此得出,对于所有的N=2n,n≥0,存在矩阵是比特反转矩阵,。
信道结合的过程只受到矩阵F的影响。同时也可以看出,GN和F⊗n的行数相同,但是顺序不同(比特翻转)。
在二进制对称信道(Binary Erasure Channel,BEC)中,可根据递推式(6)计算出子信道容量,并选择出优质子信道(非冻结比特序列)。


2.2 译码方法
极化码译码过程的本质是信道分解,从WN合成的矢量信道WN后,信道极化的下一步是将WN拆分回一系列二进制相关信道,根据当为输出,为输入时,转移概率为

本文引入了加入循环冗余校验序列(Cyclic Redundancy Check,CRC)的CRC-SCL译码算法,该算法是一种基于传统连续消除(Successive Cancellation,SC)译码算法的改进算法。
SC译码是极化码译码的基本方式。主要思想是利用F⊗n操作过程中对各个信道产生的相关性,根据输出序列和前面的i-1个序列的信息得到第i个比特。
给定一个任意与(N,K,A,uAc)相关的陪集码GN,信源由随机部分uA和冻结部分编码后得到,再通过WN信道发出,信道输出端接收到的信号为。而译码器的目的是根据得到的估计值。可以将解码器视为N个决策元素(Decision Elements,DEs)组合,源元素为ui;DEs按照1到N的顺序被激活。

根据似然比得到:

并由此迭代计算得出所有的DE。
根据极化码信道分解的特点进行简化可以得到:

因此,长度为N的LR计算,可以分解成为2个长度为N/2的计算,这种迭代过程最终可以缩减成为长度为1的计算,也就是。

图5为极化码译码原理的蝶形图,根据图5可得到,在实际的译码过程中总共须要计算N(1+log2N)个LR值。
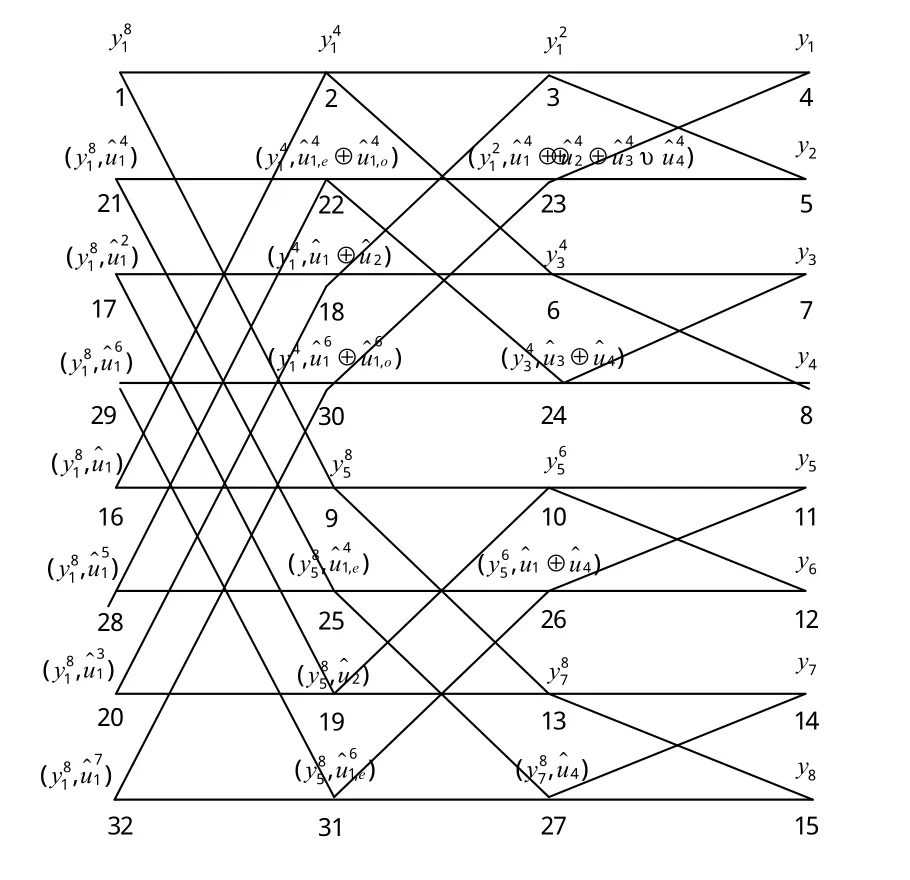
图5 译码原理蝶形图Fig.5 Decoding principle butterfly diagram
以蝶形图为基础进行LR分解,以参数(N,K,A,uAc)的{8,5,{3,5,6,7,8},(0,0,0)}为例,如图5所示。图中每个结点对应2个标签值。图中每个节点对应2个标签值:LR的值以及求解顺序,按照从左到右的顺序,从每个蝶形单元左上角的节点为起始进行计算,向右检索。例如,求解节点1的LR值需要根据节点2和节点9的LR值得出,按照深度优先的原则,可以到整个蝶形图的求解顺序。保留似然比最大的路径成为最终的输出结果。
由于SC译码算法采用的译码方式为硬判决方式,因而前序码字判决产生的错误会传递到后续码字的判决中,在中短码长的条件下,译码效果相比Turbo码和LDPC码没有优势。因此,引入SCL译码算法。
SCL译码是通过在SC译码的过程中同时保留L条候选路径的方式,对信息比特的两种取值都进行考虑,使得路径错误得到有效减少。图6是码长为4,信息比特长度为2,保留路径L=2时的模型,可称之为码树T。

图6 N=4,K=2,L=2时SCL译码算法Fig.6 SCL decoding algorithm whenN=4,K=2,L=2
在译码过程中,所有可能的译码路径同时进行译码,译码过程中只保留可能性最大的L条路径进行剪枝操作。既减轻了上层误判对后续造成的不良影响,又降低了译码复杂度。
CRC-SCL译码则是以SCL译码为基础,引入循环冗余校验序列(Cyclic Redundancy Check,CRC)[18]。按照广度优先的原则保留具有较大路径度量值的译码序列作为候选译码序列集合,最后这个集合中选出能够通过CRC校验的最大译码序列,输出从中提取到的信息比特,译码原理如图7所示。
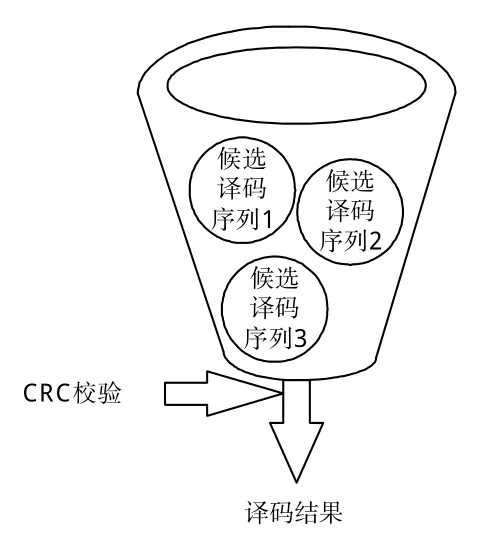
图7 CRC-SCL译码原理Fig.7 CRC-SCL decoding principles
3 仿真结果及分析
以码长1 024为例进行极化后的子信道的仿真,信道容量分布如图8所示,可以看出极化后的信道分布呈现两极分化状态,信道编号小的子信道容量趋近于0,信号编号大的子信道容量趋近于1,位于位置居于中间的信道不能完全极化。
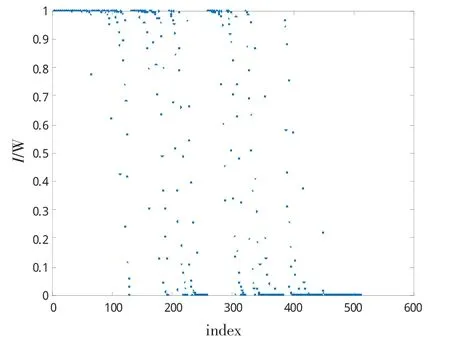
图8 极化后子信道分布(N=1 024)Fig.8 Polarization subchannel distribution(N=1 024)
在湍流强度为0.2的信道下,对码率为0.5的不同码长方案进行仿真,并与未编码的系统进行对比图9为相同码率不同码长情况下,引入极化码编译码的无线光通信系统在大气弱湍流光通信信道下的误码性能仿真。有仿真结果可知,未引入极化码编译码的系统在信噪比为15 dB时,误码率仅为约0.001。引入极化码编译码技术之后,系统可靠性得到明显改善,相较于未编码系统,在误码率同为10-3数量级时,码长为2 048,码率为0.5的编码系统可以获得约6.3dB的编码增益。通过相同码率不同码长的系统性能对比可得,在码率不变的情况下,码长越长,编码增益越大。与码长为512的编码系统相比,在误码率为10-4时,码长为2 048的编码系统在误码性能方面存在约0.9dB的优势。
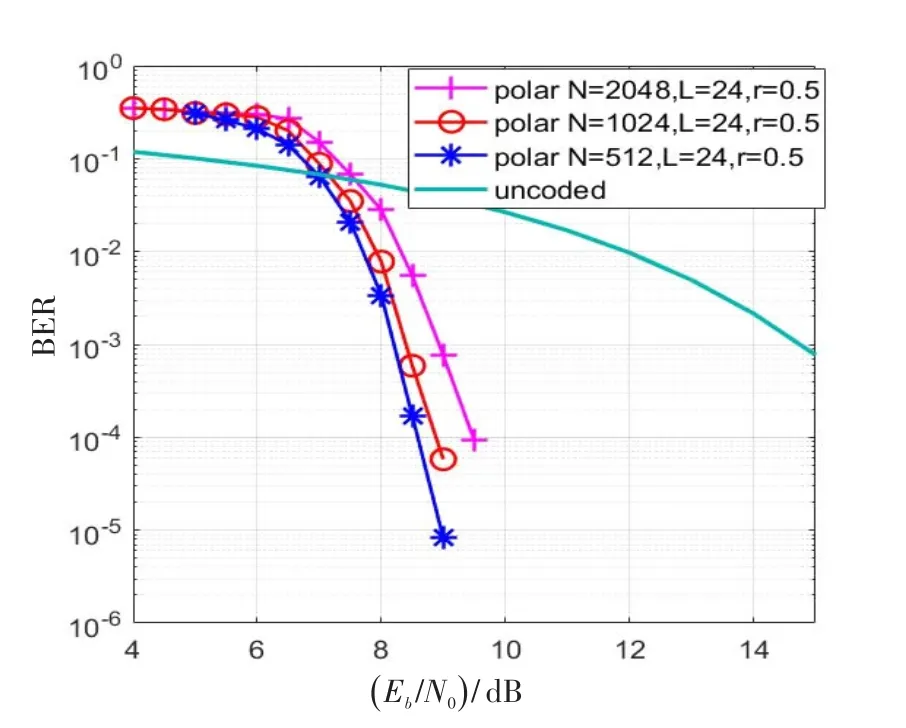
图9 不同码长条件下系统误码性能Fig.9 BER at different code length
图10为相同码长不同码率情况下,引入极化码编译码的无线光通信系统在大气弱湍流光通信信道下的误码性能对比。有仿真结果可知,在码长不变的情况下,码率越小,系统误码性能越佳。这是由于码率越小,编码冗余越大,通过降低更多的系统有效性来提高系统的可靠性。与码长为2 048,码率为0.75的编码系统相比,在误码率同为10-4时,码长为2 048,码率为0.25的编码系统在误码性能方面存在约2.8dB的优势。
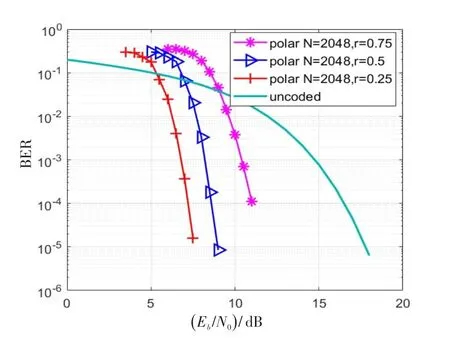
图10 不同码率条件下系统误码性能Fig.10 BER at different code rate conditions
4 结束语
本文分析了大气湍流效应对无线光通信系统可靠性的影响,研究引入极化码编码方法提高系统通信可靠性。构建了基于极化码的无线光通信系统模型,分析了极化码的基本原理和实现过程,并采用相比传统SC译码算法复杂度较低且性能更优的CRC-SCL算法进行译码。在此基础上,在不同码长和码率下,对Polar码无线光通信系统的误码性能进行了蒙特卡罗仿真分析,结果表明,Polar码在长码长、低码率的条件下具有更好的误码性能。

