无人机遥感图像融合算法综述
王海鹏,么鸿原,林雪原,郭 强
(海军航空大学,山东烟台264000)
如今,航天遥感技术已经变成人们获取特定地域地理信息及环境信息的重要手段之一[1],将无人机作为遥感平台更是被广泛应用于灾害监测、环境侦察等方面[2]。与其他遥感平台相比,无人机具有体积小、时效性强、操作灵活、成本低等明显优势[3];但无人机遥感图像单张的覆盖区域较小,对目标区域的观测图像数目过多,图像与图像之间重叠较大。因此,将无人机所拍摄的遥感图像拼接融合形成一幅广视野的全景图像有利于对目标区域进行分析[4]。
目前的遥感图像拼接融合技术可分为“像素级”“特征级”“决策级”3个级别[5];为最大程度保留图像信息要素细节,减小拼接融合过程中所造成的信息丢失的原则,无人机遥感图像的融合应采用像素级的融合方法[6]。
本文对一些常见的像素级融合方法进行了分类介绍,重点介绍了3种经典的图像融合方法。同时,介绍了可以根据哪些指标对一幅图像从主观与客观两方面进行评价;在实验阶段,对3种经典融合方法进行了实验验证与性能分析。
1 研究现状
在无人机遥感图像融合中,如果对遥感图像直接进行暴力拼接,那么不可避免地会产生拼接缝隙明显、鬼影、虚影、模糊等现象[7],严重影响拼接效果。因此,通过某种融合算法,有效地避免或消除以上情况的出现,实现待拼接图像之间重叠部分的色彩纹理等重要信息能够平滑过渡成为了当下主要研究问题[8-9]。
像素级融合又可根据空间域和变换域对各种方法进行分类:如,空间域融合方法包括逻辑滤波法[10]、加权平均法[11]、主成分分析(PCA)法[12]、HIS空间图像融合法[13]、羽化融合法[14]等;变换域图像融合法包括多分辨率融合法[15](即金字塔分解法)、小波变换法[16]等。
1.1 逻辑滤波法
逻辑滤波法是将图像间的2个像素值直接进行逻辑运算,从而合为一个像素值的最直观的融合方法。例如,当2个像素值均大于某一特定阈值(门限值)时,进行“与”运算,此时“与”滤波器输出为“1”,即图像通过“与”滤波器获得的特征可以认为是环境中十分显著的成分(即主要方面);相同的,当2个像素并不都大于特定阈值时,可通过“或”运算进行图像分割;当2个像素值均小于特定阈值时,进行“或非”运算。
1.2 主成分分析(PCA)法
主成分分析PCA方法是指对图像作多维正交线性变换,找出几个综合变量代替原来众多的变量使其尽可能代表原来变量的信息量。并在此基础上,进一步进行统计分析。
假设对m个波段的多光谱图像进行主成分变换,将图像中m个波段的相同位置的m个像素值看作其m个特征值,则可得到一幅图像的m个特征向量为:
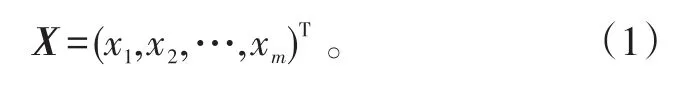
若图像的大小为N×M,那么就会有K维矢量,其中K=MN;求出其协方差矩阵:

求出λ1≥λ2≥…≥λm为Cx的m个特征值,u1,u2,…,um为其m个特征向量,可得主成分分量为:

1.3 HIS空间图像融合法
HIS是指通过亮度(Intensity)、色调(Hue)、饱和度(Saturation)3个分量对图像色彩进行描述的彩色空间。HIS空间融合能够保留图像的光谱信息特征,有效增强图像配准精度。
以TM多光谱图像与全色波段图像进行HIS图像融合为例,其一般步骤为:
1)对TM图像进行HIS变换得到图像的I、S、H分量;
2)将得到的I(亮度)分量与全色图像依照一定规则进行融合运算,例如几何配准,得到新的分量I′;此时,把I′、H、S3个分量HIS逆变换回到RGB空间,在得到了新图像的同时,还兼具高空间分辨率与高光谱分辨率的RGB图像,即融合完成。
1.4 HIS空间图像融合法
小波变换是一种建立在Fourier理论的基础上的新的变换分析方法。图像在经过小波变换分解后也会得到来自各个频段的图像信息,式(4)中为h(x)基本的小波函数。
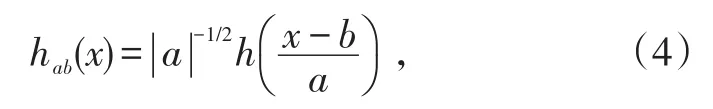
式(4)中:a是小波变换的伸缩因子;b是平移因子,且a,b∈R,a≠0。
小波变换会根据图像的框架结构将图像分解为多个子图像,子图像中中包含着细节图像与近似图像,图1所示为小波分解后的二维塔形结构。其中,LL、LH、HL、HH分别是图像的低频近似分量、水平高频分量、垂直高频分量、对角高频分量。

图1 二维塔形结构Fig.1 Two-dimensional tower structure
采用小波变换进行图像融合就是采用小波变换进行分解与重构的过程。首先,要将各源图像进行多尺度分解(即小波变换),分解出一系列的具有不同特征的子图像;由于得到的子图像无论在空间域还是频率域的特性都不相同,可以根据这些特征信息获取相应的小波系数;按照某种融合准则将各源图像的小波系数融合。此时,做小波逆变换即可得到融合图像。其融合过程如图2所示。
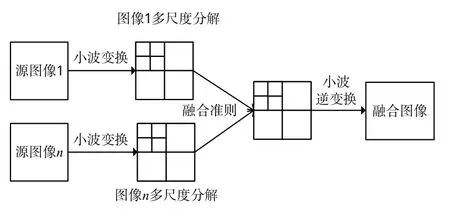
图2 小波变换的融合过程Fig.2 Wavelet transform fusion process
2 3种经典的图像融合算法
2.1 加权平均融合算法
加权平均融合算法核心在于权重的选择与分配,即所谓的“权”的确定,也称“加权系数”。这样,在融合计算时,可根据不同像素点的重要程度对2幅图像重叠区域内的像素乘上对应的加权系数,再求和。[9]
常用的2种加权融合算法有:指数函数加权融合算法、渐入渐出式的加权融合算法。通常情况下,均选用渐入渐出式的加权融合算法。具体如下:

在2幅图像融合的过程中,假设两幅图像的拼接顺序是f1→f2,在重叠区域内,k1由1逐渐减小为0,k2由0逐渐增加至1,即在最初的非重叠区域内,先取f1的像素值,重叠区域开始融合时,f1所占的比重逐渐减少。同时,f2所占的比重逐渐增加。最后,离开重叠区后,取f2的像素值,完成了2幅图像重叠区域的平滑过渡。

图3 渐入渐出式权值变化图Fig.3 Gradual fade-in weight change graph
2.2 羽化融合法
羽化融合算法是通过对2幅图像的重叠区域中在拼接线周围一定范围内的区域进行融合处理的算法。其原理为:将其中一副图像记作img1,将另一幅记作img2;将2幅图像的重叠区域记作Over1,羽化融合就是指将重叠区域的边界由img1平滑过渡到img2,即完成了由img1到img2的拼接融合;反之,则完成由img2到img1的拼接;将过渡区域记作Trans;融合过渡过程如图4、5所示。
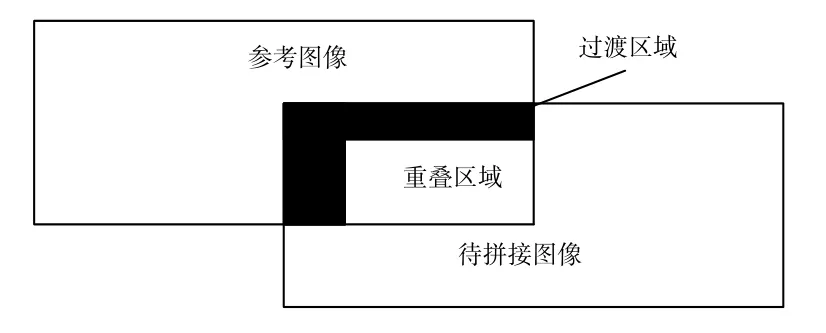
图4 由参考图像过渡Fig.4 Transition from reference image

图5 由待拼接图像过渡Fig.5 Transition from image to be stitched
羽化融合的步骤如下:
1)计算过渡步长s:将img2中重叠区域内的重叠边界行像素值记作m,将img2中重叠区域内的Trans行的像素值记作l,可通过式(6)计算得到过渡步长。

2)计算融合后过渡区域的像素值:融合后过渡区域中第Trans行的像素值为l+s,第Trans-1行的像素值为l+2×s,第Trans-2行的像素值为l+3×s,以此类推,最后过渡区第1行的像素值将变成l+Trans×s。此时,重叠部分上边界的过渡完成。侧边界同理。
2.3 多分辨率融合法
多分辨率图像融合法也被称作金字塔图像融合法,最早提出的多分辨率算法是基于Laplacian金字塔的金字塔分层结构将图像之间的重叠部分互相对应的分解到各个频域中进行操作;通过将图像分解到不同的频域,使接下来的操作能够极好地避免图像信息丢失,避免图像失真,保存图像细节信息完整。多分辨率融合方法的大致流程如图6所示。

图6 多分辨率融合过程Fig.6 Multi-resolution fusion process
3 图像融合性能评价
融合后图像质量的优劣与图像融合方法直接相关,对于图像融合性能的评价方法一般分为主观和客观2类[17]。主观方法主要是通过人眼的观察来评价融合后图像的质量;而客观方法主要指的是通过一系列的计算得到相应的数据来定量的评价图像融合质量。客观方法又分为无参考图像的评价方法和有参考图像的评价方法。本文针对无参考图像的评价方法进行介绍。
3.1 图像融合的主观评价
图像的主观评价,顾名思义是指当人看到融合后图像的主观意识,是依靠人眼对图像进行观察而得出的评估结果[18]。虽然这种方法对于观察者来说简单直观,但过于依赖人的主观意识,不同人观察可能会有不同的评价结果,且人眼无法分辨图像的细节差异,对于色彩的细微变化也不敏感。因此,在评价图像时,还需要引入客观指标进行定量的客观评价。
3.2 图像融合的客观评价
由于图像中含有丰富的信息,因而选取不同的参数进行评价所得到的结果有可能不同。因此,在进行客观评价时,一般针对某个或某几个侧重的方向选取特定的参数指标进行计算评价[19]。下面介绍一些常用的客观评价参数。
1)熵EN。图像的熵值代表着图像所携带信息量,熵越大,表示图像携带的信息越多,定义为:

式(7)中:L代表图像的灰度级别;p(g)代表灰度值g像素占总像素的比例。
2)空间频率SF。图像的空间频率大小表示图像活跃程度的高低,定义为:

式(8)中:RF为行频率;CF为列频率。
3)信噪比SNR。假定融合图像与参考图像之间的差异为噪声,信噪比越大代表融合图像的质量越好,定义为:

式(9)中:S为信号方差;N为噪声方差。
4)峰值信噪比PSNR。一般情况下,图像的峰值信噪比越大,表示融合图像质量越好,失真越少,定义为:

式中,MSE为图像均方误差。
5)标准差SD。标准差代表图像像素信息的丰富程度,值越大图像中像素信息越丰富,定义为:
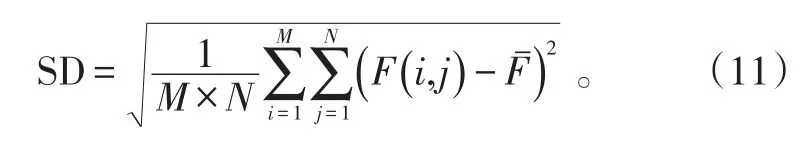
式(11)中:M是图像的宽;N是图像的高;F(i,j)是图像的像素值;是图像像素均值。
6)平均梯度AG。平均梯度与空间频率相似,反映的都是图像的清晰程度;平均梯度越大,图像越清晰,定义为:
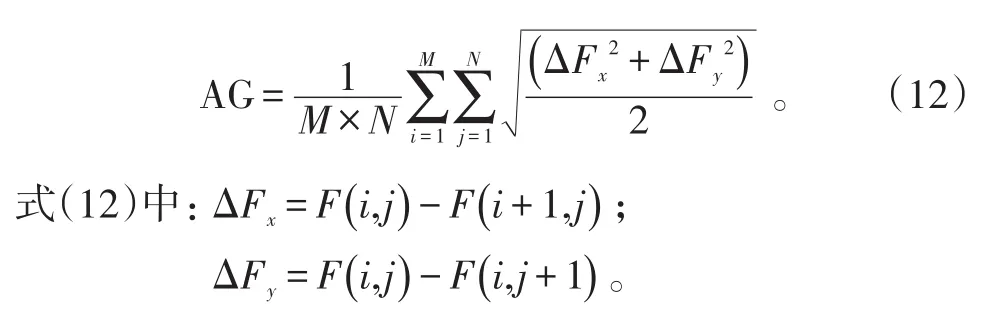
4 实验结果与分析
本文对3种经典的像素级融合算法:加权平均融合、多分辨率融合、羽化融合进行测试及评价,实验平台为个人计算机,配置为Intel Core i5-2450M 2.5 GHz,4 GB内存,操作系统为64位Windows7,算法基于OpenCV2.4.10,用C++进行编程并在Visual Studio 2010中进行实验。实验数据为120张大疆无人机航拍获得,图像格式为JPEG。
4.1 主观评价
图7中给出了4张结果图。观察图7可知,未采用融合方法[20]的拼接图像拼接缝隙明显,颜色过渡十分突兀且拼接错位;采用多分辨率融合算法使重叠部分色彩过渡平缓,几乎看不出拼接缝隙,且拼接准确;采用加权融合算法虽然拼接准确,但颜色纹理过渡突兀,拼接线明显;采用羽化融合方法虽然颜色纹理过渡相对平缓,但重叠区域的拼接线周围出现一定的图像变形、鬼影。从主观分析结果来看,多分辨率融合法的融合效果明显优于其余2种方法。

图7 融合效果及细节放大图Fig.7 Fusion effect and detailed enlarged view
4.2 客观评价
在实验中,本文对120张无人机遥感图像采用金字塔结构,将其分解出的第一层图像分别采取3种融合方法进行融合,每种融合方法进行一组实验,并对每组实验得到的60幅融合结果图计算出前文所提到的6项客观评价指标的平均值,即得到实验中各项参数的统计特性,并进行客观分析及评价。

表1 各项融合指标Tab.1 Various integration indicators
表1中,黑体加粗为最优。从6项指标中可以看出来,在熵值、信噪比、峰值信噪比、标准差4项评价中,多分辨率融合方法最优,其次是羽化融合方法,加权平均方法最差;在空间频率、平均梯度两项评价中,加权融合方法最优,其次是羽化融合、多分辨率融合法最差,但由前文分析可知,空间频率与平均梯度表示图像中像素活跃程度的高低,观察融合图像可知,是由于加权融合方法并不能使图像的色彩及纹理能够平缓过渡,因而影响到图像中的像素活跃程度会高于其余2种方法。而由于多分辨率融合方法基本上完成了颜色及纹理的平滑过渡,在空间频率及平均梯度两项评价中数值较低。
结合主观评价与客观评价两方面的评价结果,总体上,采用多分辨率融合方法得到的融合图像拼接准确,色彩过渡平缓基本无色差,图像清晰,细节能够大量保留。其融合效果要优于羽化融合方法及加权平均融合方法。
本文对各种算法的运行时间也进行了数据统计,3种融合方法在对120幅遥感图像的金字塔结构第一层直接融合所用时间如表2所示。由表2可知,多分辨融合方法虽然融合效果要优于加权融合方法及羽化融合方法,但其运算复杂度也导致运行时间也远远大于其余2种算法。

表2 融合算法运行时间Tab.2 Fusion algorithm runtime s
5 总结
本文对一些常见的像素级图像融合法进行了介绍,并重点介绍了3种经典融合方法,同时介绍了根据哪些指标对对1幅图像从主观与客观两方面进行评价;通过对3种经典融合方法进行实验分析可知,多分辨融合方法融合效果要优于加权融合方法及羽化融合方法,其运算复杂度也导致运行时间也远远大于其余2种算法。这充分说明了采用评价指标对融合方法进行优劣性评价的有效性。因此,在实际的应用中,应根据需要选择合适的融合算法进行改进。

