基于样本加权FCM聚类的未知类别局部放电信号识别

贾亚飞，朱永利，高佳程，袁 博

(1. 华北电力大学 新能源电力系统国家重点实验室，河北 保定 071003；2. 国网河北省电力有限公司雄安新区供电公司，河北 雄安新区 071800；3. 国网河北省电力公司经济技术研究院，河北 石家庄 050000)

0 引言

电力变压器是电力系统输变电的关键性设备，其运行的可靠性直接关系到整个电力系统的安全与稳定。变压器故障统计分析表明[1]，绝缘故障是影响变压器可靠运行的重要原因之一，而局部放电是导致变压器绝缘破坏的主要原因。不同类型缺陷产生的局部放电具有不同的特征[2-3]，因此对局部放电信号进行有效的模式识别，可以准确地了解和掌握变压器内部缺陷类型的性质和特征，对指导变压器的检修工作意义重大。

分类器的设计是实现局部放电模式识别的关键环节之一，主要分为无监督模式识别和有监督模式识别两大类。聚类分析是无监督模式识别中的一个重要分支，文献[4]利用模糊C均值FCM(Fuzzy C-Means)算法针对提取的特征向量对放电源脉冲进行聚类，取得了较好的聚类效果；文献[5]提出了基于K-means聚类分析的局部放电谱图自动识别方法，经现场实际测试数据和在线监测数据测试证明，该方法在相位信息缺失的情况下能够实现对局部放电监测数据的自动诊断分析，得到局部放电谱图的识别结果；文献[6]利用Mahalanobis距离算法系统地阐述了各类放电在三角坐标系中的聚类分布情况，实现了对典型局部放电信号模式的准确识别。常用的有监督模式识别方法有支持向量机SVM(Support Vector Machine)、神经网络、相关向量机等。文献[7]提出了一种基于多分组特征的组合核多分类SVM的局部放电信号识别方法，寻找最优核函数组合分类模型，对多个特征空间数据具有普适性，且融合效果理想。文献[8]提出了一种基于自适应小波神经网络的局部放电信号识别方法，构建了一个4层自适应小波神经网络模型，并且采用粒子群优化算法进行一次优化，采用BP算法进行二次优化，研究结果表明该方法的训练效果明显优于单独使用BP算法的训练效果。文献[9]采用多分类相关向量机M-RVM(Milticlass Relevance Vector Machine)实现局部放电信号的多分类问题，该方法的基函数权值少数非零，诊断速度快，可以有效解决小样本、高维、非线性分类问题。无监督的模式识别方法虽然可以有效、快速地进行局部放电信号的划分，但是这一诊断过程只是实现了局部放电信号的初步分析，并没有进一步给出局部放电信号的类型等信息。SVM[10-11]和神经网络[12]等有监督分类方法需要对具有明确放电类别的样本进行训练和学习，然后用训练好的分类器对待识别样本进行分类。

目前，虽然多种有监督模式识别方法已经成功应用于局部放电信号的模式识别，但是还没有关于待识别局部放电信号中存在不属于已知类别的局部放电信号，即未知类别局部放电信号识别的研究。对于变压器而言，经过长期的监测工作和经验积累，可整理得到一部分可用的具有明确类型信息的局部放电信号样本，但变压器本身的结构复杂，要想获得全部局部放电信号类型的训练样本十分困难。而有监督模式识别方法只能识别已知放电类别，如果对不属于已知类别(未知类别)的局部放电信号进行分类，该类信号会被分类到已知类别中，导致错误的诊断。因此，在对待识别局部放电信号进行分类前，有必要对待识别局部放电信号中不属于已知类别的局部放电信号进行识别。

局部放电是一个渐变的过程，提取的特征通常具有模糊性，若直接采用提取的特征值来辨识放电类型会存在一定的难度。以模糊数学为基础的聚类分析方法为解决这类问题提供了一种可行的途径。FCM是模糊聚类中应用最为广泛的一种算法，它依据数据样本间的相似度，通过迭代优化目标函数，将相似度高的样本对象划分为同一类来实现数据的分类。因此，FCM在局部放电信号模式识别中得到了广泛的应用。

基于上述问题，为了充分利用收集到的已知类别的局部放电信号，并且能有效识别不属于已知类别的局部放电信号，本文提出了一种基于样本加权FCM聚类的未知类别局部放电信号识别方法，对待识别局部放电信号进行分析。该方法根据各待识别局部放电信号与已知类别聚类中心的距离确定权值，利用Otsu准则，即采用最大类间方差法自适应地选取样本权值阈值，通过比较确定各局部放电信号是否属于已知类别，挑选得到未知类别的局部放电信号，然后对属于已知类别的局部放电信号进行分类。可以对挑选得到的未知类别的局部放电信号进行人工分析判断，确定其放电类型后将其加入已知类别的训练样本中。为了验证本文所提方法的有效性，采用SVM方法分别对所有待识别局部放电信号样本(包含未知类别的放电信号样本)和经样本加权FCM聚类方法处理后的样本进行分类。实验结果表明，经基于样本加权FCM聚类方法处理后的样本的正确识别率要远远高于直接对所有待识别样本进行分类的正确识别率，充分证明了本文所提方法可有效识别未知类别的局部放电信号样本，对局部放电信号的模式识别具有重要意义。

1 样本加权FCM聚类算法

1.1 FCM聚类算法原理

FCM算法是一种经典的基于目标函数的聚类算法，其目的是将n个样本无监督地划分为c个类别。FCM算法在传统硬聚类算法中引入了模糊技术，通过极小化所有数据点与各个聚类中心的欧氏距离及模糊隶属度的加权和，不断迭代修正聚类中心和分类矩阵，直到符合终止准则，将具有相似特性的数据样本聚为一类[13-14]。

设有一组含n个样本的样本集X={x1，x2，…，xn}，其中每个样本具有p个特征属性，即xk=[xk1，xk2，…，xkp](k=1，2，…，n)。各样本以一定的程度隶属于c个不同的区域，用隶属度μij表示第j个样本隶属于第i类的程度，μij∈[0,1]。

FCM聚类的目标函数为：

(1)

约束条件为：

(2)

其中，U=[μik]c×n为隶属度矩阵；V=[v1,v2,…,vc]为聚类中心矩阵；m∈[1,∞)为平滑参数，一般取m=2；dik为样本xk到聚类中心vi的距离，dik=‖xk-vi‖。

FCM算法的求解过程中，在式(2)所示约束条件下，算法通过不断迭代来更新聚类目标函数值、聚类中心和隶属度矩阵，以最小化目标准则，直至聚类中心不再变化或2次迭代的目标函数值之差在允许的范围内，其中目标函数值误差采用默认参数10-5。得到的隶属度和聚类中心分别如式(3)、式(4)所示。

(3)

(4)

可以通过分离系数和分离熵2个性能指标进行聚类效果检验，其定义分别如式(5)、式(6)所示。

(5)

(6)

分离系数F和分离熵H中包含了隶属度信息。分离系数F越接近于1，则聚类效果越好；分离熵H越接近于0，则聚类效果越好。

1.2 样本加权FCM聚类算法

在传统的聚类算法中，所有样本都同等地参与聚类过程。然而，待聚类样本集合中的每个样本在聚类过程中所起的作用并不一样，对聚类结果产生的影响也有所不同。样本加权FCM聚类算法通过为离群点赋予很小的权值，降低离群样本点参与聚类过程的程度，从而削弱离群样本点对聚类效果的影响。

样本权值的确定主要有2种方法，可以根据实际需要进行选择。

第1种权值计算方法是描述样本点相互之间的接近程度，计算公式如式(7)所示。

(7)

其中，α为常数；j=1，2，…，n。

第2种权值计算方法描述各样本与各聚类中心的接近程度，计算公式如式(8)所示。

(8)

2 基于样本加权FCM聚类的未知类别局部放电信号识别方法

由于电力变压器的结构复杂，对于收集到的待识别局部放电信号集合中可能存在不属于已知放电类别的未知放电信号，若直接进行分类，会将其分到已知放电类别中，导致误诊断。因此，有必要在对待识别放电信号进行分类前挑选出不属于已知类别的放电信号。本文基于样本加权FCM聚类算法的思想，计算各待识别放电信号的权值，然后根据各样本权值的大小判断样本是否属于已知类别。待识别局部放电信号样本权值和权值阈值的确定是实现该方法的2个关键步骤。

2.1 样本权值计算

1.2节给出了2种样本权值的计算方法，第1种方法(式(7))是通过计算每个样本点与其余样本点的距离来定量描述样本在整个样本集中的位置，该方法虽然在一定程度上可以刻画样本点相互之间的接近程度，但是计算量比较大，并且没有充分利用已知类别的样本信息；第2种方法(式(8))是通过计算样本与各个已知类别样本的聚类中心的距离来描述样本对各聚类中心的接近程度，该方法对聚类中心比较敏感，当聚类中心较为准确时权值才会更加合理。

本文所提基于样本加权FCM聚类的未知局部放电信号识别方法首先得到已知类局部放电信号的聚类中心，即可以确定准确的聚类中心，因此，本文选用第2种方法计算样本权值。

2.2 样本权值的自适应阈值选取方案

根据待识别局部放电信号样本权值的大小可以将待识别样本划分为已知类别样本和未知类别样本(与各聚类中心距离较远)2类，其中样本权值阈值T的确定是该问题的关键。由于无法掌握待识别放电信号的信息(是否属于已知类别的放电信号)，无论是设定统一的阈值还是根据经验手动设定，都无法满足待识别放电信号样本权值阈值确定的需要。本文提出一种基于Otsu准则[15-16]的自适应确定样本权值阈值T的方法，即选取某阈值T令已知类别样本和未知类别样本间的方差最大，此时2类样本之间的差异也最大，因此，该阈值T是最优划分阈值[17]。基于Otsu准则确定样本权值阈值T的基本原理如下[15-16]。

对于N个局部放电信号样本，将各样本权值看作长度为N的离散序列{wi，i=1，2，…，N}，wmax、wmin分别为该序列的最大值和最小值。

为了方便描述，引入灰度概念，即对应放电样本权值的大小。设定灰度等级L(即放电样本权值大小的等级)，令dw=(wmax-wmin)/L。统计权值大小落在[(l-1)dw，ldw]范围内的值的个数nl，其中l=1，2，…，L为灰度值，nl是灰度值为l时的像素。nl出现的概率为pl=nl/Ns，Ns=n1+n2+…+nL为总像素数。

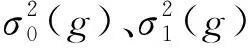
(9)

(10)

(11)

(12)

(13)

(14)

C0和C1间的类内方差之和为：

P1(g)[μ1(g)-μ(g)]2

(15)

其中，μ为整个序列的灰度均值，计算公式如式(16)所示。

(16)

则可以确定最优阈值为g*dw，令：

(17)

综合式(9)—(17)，可以得到最优样本权值的阈值，即T=g*dw。

2.3 基于样本加权FCM聚类的未知局部放电信号识别方法

本文根据局部放电信号样本的权值大小来判断该信号是否属于已知类别。分别提取已知类别的d类局部放电信号和待识别局部放电信号的特征量，得到的特征量分别构成已知类别局部放电信号样本X={x1，x2，…，xN}和待识别局部放电信号样本S={s1，s2，…，sM}，其中N和M分别为已知类别局部放电信号样本的个数和待识别局部放电信号样本的个数。

本文采用文献[18]中的变分模态分解VMD(Variational Mode Decomposition)和多尺度熵MSE(MultiScale Entropy)对局部放电信号进行特征提取。利用VMD方法对局部放电信号进行分解得到模态分量，利用MSE方法对得到的分解模态进行定量描述，形成特征向量，然后利用主成分分析法PCA(Principle Component Analysis method)对得到的特征向量进行降维处理，将其作为局部放电信号特征向量。该特征提取方法的流程图如图1所示，具体过程不再赘述。

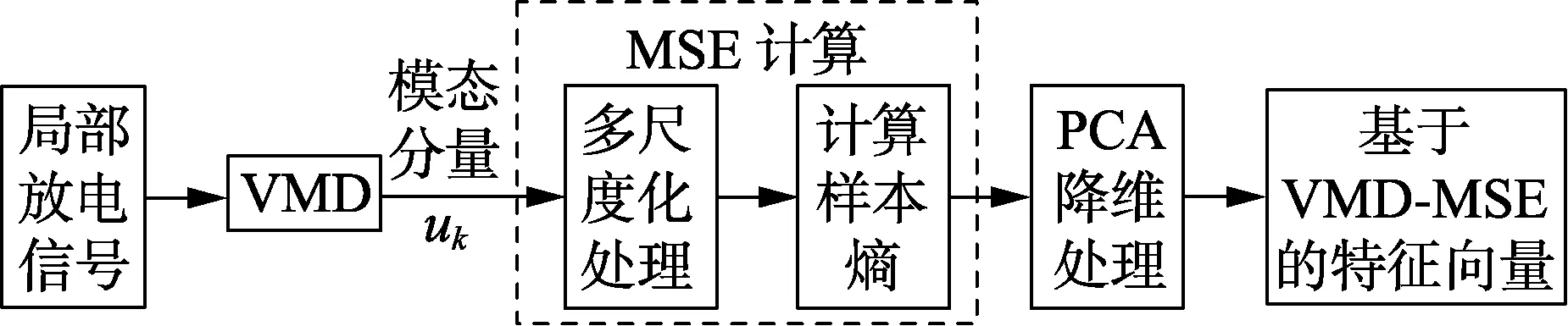
图1 基于VMD-MSE方法的特征提取过程Fig.1 Feature extraction process based on VMD-MSE method

基于样本加权FCM聚类的未知局部放电信号识别方法的流程图见附录中图A1，具体实现步骤如下。

a. 采用FCM算法对已知类别的d类局部放电信号样本进行聚类，确定各类别的聚类中心v=[v1，v2，…，vd]。

b. 根据步骤a得到的聚类中心和式(8)分别计算已知类别的局部放电信号样本和待识别的局部放电信号样本的样本权值，分别记为w_X=[w1，w2，…，wN]和w_S=[wN+1，wN+2，…，wN+M]。

c. 将待识别局部放电信号样本的权值和已知类别局部放电信号样本的权值进行组合，即w=[w_S，w_X]，根据Otsu准则确定样本权值的自适应阈值T。

d. 将待识别局部放电信号样本权值集合w_S=[wN+1，wN+2，…，wN+M]中各样本权值分别与阈值T进行比较。若wi≥T(N+1≤i≤N+M)，则该局部放电信号样本si属于已知放电类别；若wi

e. 用常规模式识别方法对待识别样本中属于已知类别的局部放电信号样本进行分类，对于属于未知类别的局部放电信号样本一一进行人为分析判断，确定其放电类型后将其归为已知类别的局部放电信号样本集中，对已知类别的局部放电信号样本集进行扩充。

3 实例分析

3.1 局部放电信号采集

本文的局部放电信号是在实验室环境下对不同放电模型进行局部放电信号检测得到的。试验采用IEC60270—2000标准，试验电路为基于脉冲电流法的并联测试电路，采用TWPD-2F局部放电综合分析仪。局部放电信号的采集频率为20 MHz，带宽为40～300 kHz。以每个工频周期记录到的数据作为一个局部放电信号。

本文中已知类别的局部放电信号集合由电晕放电模型、油中多尖对板放电模型、油中板对板放电模型和油中悬浮颗粒放电模型4种放电模型产生的局部放电信号组成，4种放电模型装置分别如附录中图A2(a)—(d)所示。未知局部放电信号集合由上述4种放电模型之外的油中锥对板放电模型产生，如附录中图A2(e)所示。

3.2 基于样本加权FCM聚类的未知局部放电信号识别

本文选取电晕放电模型、油中多尖对板放电模型、油中板对板放电模型和油中悬浮颗粒放电模型4种放电模型产生的200个局部放电信号，其中每种放电模型各产生50个局部放电信号。按照文献[18]提出的特征提取方法提取各局部放电信号的特征量，形成已知类别的局部放电信号样本集X。此外，收集100个未知类型的局部放电信号(包含80个已知类别的局部放电信号和20个未知类别的局部放电信号)，进行特征提取后得到的特征量形成待识别局部放电信号样本集S。采用本文所提基于样本加权FCM聚类的未知类别局部放电信号识别方法对待识别局部放电信号样本集进行处理。其中采用基于样本加权FCM聚类方法的关键是权值阈值的确定，此处采用2.2节介绍的Otsu准则自适应地确定样本权值阈值T。

将未经处理的待识别局部放电信号样本集和经本文所提方法处理后的样本集采用FCM方法进行聚类。聚类效果可以通过分离系数F和分离熵H这2个指标进行检验。未经处理的待识别局部放电信号样本集和经本文所提方法处理后的样本集采用FCM方法进行聚类后的分离系数F和分离熵H如表1所示。

表1 FCM的聚类效果评价指标Table 1 Evaluation indexes for clustering result of FCM

由表1可知，对经本文所提方法处理后的待识别局部放电信号样本进行FCM聚类的聚类性能指标要远远优于对未经处理的待识别局部放电信号样本直接进行FCM聚类的聚类性能指标，这充分说明了采用样本加权FCM聚类方法可以有效地改善含未知类别的待识别样本的聚类效果，验证了所提方法的有效性。

采用基于样本加权FCM聚类的未知类别局部放电信号识别方法对待识别局部放电信号样本集进行处理后，属于已知类别和属于未知类别的局部放电信号样本判断的正误情况如表2所示。由表2可知，本文所提未知类别局部放电信号识别方法将属于已知类别的局部放电信号样本全部正确分类到已知类别样本集中，属于未知类别的局部放电信号中有4个错误地分类到已知类别样本集合中。虽然本文所提方法仍然存在一定的判断误差，但已经能对绝大部分的待识别样本进行正确划分，正确率达96%，这也充分说明了本文所提方法对未知类别样本识别的有效性，为进一步的模式识别创造了先决条件。

表2 局部放电信号样本类别判断的正误情况Table 2 Right and wrong situation of type judgment for partial discharge signal samples

3.3 局部放电信号模式识别

为了进一步验证本文所提方法的有效性，本文采用SVM分别对未经处理和采用本文所提方法处理后的局部放电信号样本集进行分类。SVM中核函数选取径向基(RBF)核函数，参数均取最优，其中惩罚参数为5，核参数为0.2。分类结果如表3所示。由表3可知，对未经处理的待识别放电信号样本集直接利用SVM进行分类，虽然样本集中各已知类别样本的正确识别率均为100%，但总体正确识别率却只有80%。这是因为待识别样本集中含有一部分不属于已知类别的局部放电信号，直接用SVM进行分类会将这部分样本错分为已知类别，从而造成误判。而经本文所提方法处理后的待识别样本经SVM进行分类后，总体正确识别率提高到95.24%。实验结果充分验证了本文所提基于样本加权FCM聚类的未知局部放电信号识别方法可有效地处理待待识别样本集中的未知类别信号，提高局部放电信号识别的准确率。

表3 基于SVM的识别结果Table 3 Recognition results based on SVM

4 结论

a. 本文提出了一种基于样本加权FCM聚类的未知类别局部放电信号识别方法，实现对待识别局部放电信号中未知类别样本的识别。采用FCM聚类确定已知类别局部放电信号样本的各类聚类中心，计算局部放电信号的样本权值，将各待识别局部放电信号的权值与确定的阈值进行对比，判断其是否属于已知类别。

b. 提出了根据Otsu准则确定样本权值的自适应阈值，为样本权值阈值的确定提供了一种可行方案。

c. 采用基于样本加权FCM聚类的未知类别局部放电信号识别方法对待识别局部放电信号进行处理，将得到的属于已知类别的待识别局部放电信号采用SVM进行分类。将结果与未经处理的待识别局部放电信号直接进行SVM分类的结果进行比较，结果表明，采用本文所提方法处理后的局部放电信号具有较高的正确识别率，为未知类别局部放电信号的识别提供了一条有效的解决途径。

附录见本刊网络版(http:∥www.epae.cn)。