基于两阶段鲁棒区间优化的风储联合运行调度模型

张刘冬，袁宇波，孙大雁,袁晓冬，李 强，苏大威

(1. 国网江苏省电力有限公司电力科学研究院，江苏 南京 211103；2. 河海大学 能源与电气工程学院，江苏 南京 211100；3. 国网江苏省电力有限公司，江苏 南京 210024)

0 引言

由于风电的随机性和低可预测性以及源网的不协调发展，许多国家和地区的弃风现象比较严重。通过将储能系统(包括电化学储能装置、抽水蓄能机组等)与风电场联合运行，提升风电的消纳水平受到了广泛关注[1]。当前国内外学者[2-9]在风储联合运行的优化调度方面已进行了大量的研究工作。

针对风电不确定性的不同处理方式，可将其归纳为4类方法：确定性方法[2-3]、模糊数学方法[4]、随机规划方法[5-6]和鲁棒优化方法[7-9]。其中，确定性方法虽简单，但忽略了风电出力不确定性的影响，难以兼顾风储联合运行的经济性和可靠性。文献[4]提出了基于相关机会目标规划的风光储联合运行调度策略，但将风电的出力表示为确定性功率值和具有模糊性的误差值之和需要进一步商榷。随机规划方法[5-6]依据风电功率预测误差，模拟未来风电的出力场景，但实际运行中难以准确获取风电预测误差概率分布，并且为了达到较高的求解精度需要抽样出海量场景，限制了其大规模应用场合。鲁棒优化方法采用不确定参数集描述风电的不确定性，该区间集合在实际中容易获得，而且模型求解效率高，求解结果考虑了最极端情况，安全性可以保证。但文献[7-9]尚无法从系统旋转备用约束和网络安全约束方面优化风电波动区间，难以全面和准确地考虑风电消纳能力对常规机组和储能系统运行方式的影响。

为此，本文在不确定区间可优化的双层鲁棒区间经济调度模型[10]中加入常规机组和储能系统运行状态的离散决策变量，构建风储联合运行的双层鲁棒区间机组组合模型，并提出基于Benders分解算法的两阶段迭代求解策略。具体地，通过将离散和连续变量分别作为第1阶段和第2阶段的决策变量，消除两者间的耦合关系，再根据线性对偶理论，将构建的双层模型等效转化为单层两阶段模型，并利用Benders分解算法对两阶段模型进行逐次交替迭代求解。在含风电场的IEEE-RTS 26机测试系统上进行蒙特卡洛仿真，验证了所提模型及算法的有效性和优越性。

1 风储联合运行的鲁棒区间调度模式

图1 风储联合运行的鲁棒区间调度模式示意图Fig.1 Schematic diagram of robust interval dispatch mode for joint operation of wind-storage system

2 双层鲁棒区间机组组合模型

2.1 目标函数

风储联合运行调度模型一般以最小化常规机组的发电成本FGC、储能系统运行成本FSC以及弃风惩罚成本FWC为目标函数，如式(1)所示。

min{FGC+FSC+FWC}

(1)

常规机组的发电成本包括出力成本、旋转备用成本以及开停机成本3个部分：

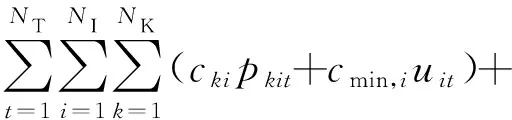
(2)

FSC包括充放电成本和循环成本：

(3)

为了最大限度地减少弃风，需要对预测出力上下界与允许出力上下界之间的偏差进行惩罚，惩罚成本的表达式为：

(4)

其中，NW为风电场数目；Vw为对风电场w的上下界偏差惩罚成本系数。

2.2 约束条件

a. 功率平衡约束。

(5)

b. 常规机组的出力上下限约束。

(6)

其中，pmin,i、pg,1i、pg,2i、…、pg,(NK-1)i和pmax,i为将常规机组i的出力范围[pmin,i,pmax,i]线性化NK段后的功率分点。

c. 常规机组的最小开停机时间约束。

引入机组i在初始阶段需保持开机状态的调度时段数，记为UTi，计算式如下：

(7)

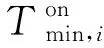
uit=1t=1,2,…,UTi

(8)

(9)

(10)

其中，sit为二元整型变量，机组i在第t时段处于开机过程时其值为1，否则为0。

同理，引入机组i在初始阶段需保持停机状态的调度时段数，记为DTi，计算式如下：

(11)

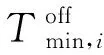
uit=0t=1,2,…,DTi

(12)

(13)

(14)

其中，dit为二元整型变量，机组i在第t时段处于停机过程时其值为1，否则为0。sit、dit和uit满足如下关系：

sit-dit=uit-uit-1

(15)

sit+dit≤1

(16)

此外，目标函数式(1)中机组i的开机和停机成本则可分别线性化为csu,isit和csd,idit。

d. 旋转备用约束。

(17)

(18)

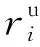
违反常规机组的旋转备用约束会导致弃风。从系统动态响应能力的角度分析，风电功率突变会减小常规机组的旋转备用容量，导致系统安全水平降低，因而该场景也就越恶劣，由此构成判别最恶劣场景的式(19)—(22)。

(19)

(20)

(21)

(22)

e. 常规机组的爬坡率约束。

从系统动态响应能力的角度，最恶劣场景下常规机组的爬坡率约束为：

(23)

(24)

(25)

(26)

(27)

(28)

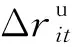
f. 网络安全约束。

违反网络安全约束也会导致弃风。从网络安全的角度分析，风电出力在边界取值时会增大线路负载率，导致系统安全水平降低，因而该场景也就越恶劣，由此构成判别最恶劣场景的式(29)和式(30)。

(29)

(30)

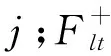
g. 风电允许出力区间和风电出力约束。

(31)

(32)

h. 储能系统运行约束。

(33)

(34)

(35)

(36)

(37)

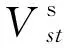
(38)

3 基于Benders分解算法的迭代求解策略

在第2节建立的双层鲁棒区间机组组合模型中，下层优化模型式(19)、(21)、(29)、(30)含有“min”和“max”极值问题，不利于直接求解。因此需要基于线性对偶理论，对含有“min”和“max”的表达式进行等价转化，将双层模型转化为单层模型来求解[10]。但由于上下层模型存在常规机组、储能系统运行状态离散变量和连续变量的耦合关系，下层模型不仅仅是上层模型的最大或最小发电能力约束，因此原经济调度模型中适用的双层模型向单层模型转化的对偶转换过程在机组组合中会失效，导致双层机组组合模型难以求解。为此，本节首先通过将离散变量作为第1阶段决策变量，连续变量作为第2阶段决策变量，消除两者间的耦合关系，然后根据线性对偶理论，将第2节的双层鲁棒区间机组组合模型等效转化为单层两阶段鲁棒区间机组组合模型，最后利用Benders分解算法对两阶段模型进行逐次交替迭代求解。

3.1 单层两阶段鲁棒区间机组组合模型的构建

为了便于描述两阶段鲁棒区间机组组合模型的建立过程以及基于Benders分解的求解算法，首先将第2节的双层模型采用紧凑表达形式描述如下：

(39)

s.t.Fx≤f,Ex=e

Hy≤h,Ax+By≤m,Ix+Jy=n

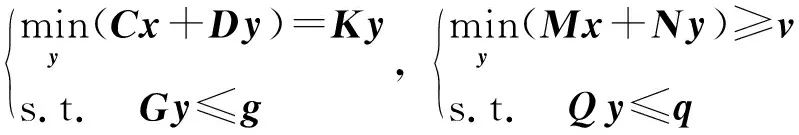
(40)

x={xi|xi∈{0，1}},y≥0

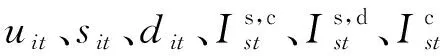
单层两阶段的鲁棒区间机组组合模型的具体构建步骤如下。

步骤1 将离散变量向量x和连续变量向量y分别作为第1阶段和第2阶段的决策变量，则双层模型式(39)和式(40)等效为如下双层两阶段模型：

(41)

s.t.Fx≤f,Ex=e,x={xi|xi∈{0,1}}

(42)

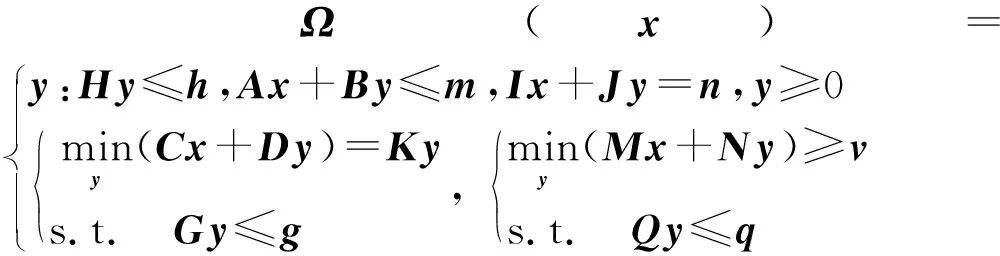
(43)

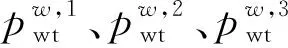
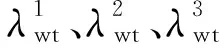
(44)

(45)

(46)

(47)

Ω′(x)={z:Lz≤l,Px+Sz≤p,Wx+Vz=w,z≥0}

(48)

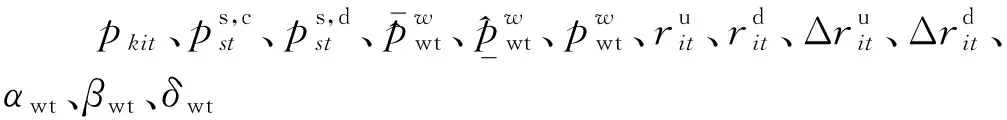
最终获得与原双层鲁棒区间机组组合模型式(39)和式(40)等价的单层两阶段鲁棒区间机组模型：

(49)

s.t.Fx≤f,Ex=e,x={xi|xi∈{0,1}}

(50)

3.2 基于Benders分解算法的两阶段迭代求解策略的计算步骤

(51)

s.t. -STω-LTη+VTχ≤b

ω≥0,η≥0,χ无约束

(52)

其中，ω、η和χ为变量z的对偶变量。对偶子问题的可行解集式(52)与离散变量x无关，且根据对偶理论，两阶段鲁棒区间机组组合模型可表示为：

(53)

s.t.Fx≤f,Ex=e,x={xi|xi∈{0,1}}

(54)

设Benders子问题的可行解集式(52)的极点集为HP，极方向集为HR，引入松弛变量θ，构造两阶段鲁棒区间机组组合模型式(53)和式(54)的Benders主问题：

(55)

s.t.Fx≤f,Ex=e,x={xi|xi∈{0,1}}

(56)

(57)

(58)

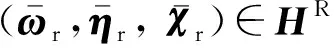
(59)

式(57)和式(58)分别为连接主、子问题的Benders最优性割平面和可行性割平面。

参考文献[12]，基于Benders分解的求解方法流程如图2所示。首先初始化：设置迭代计数k=1，给定初始上界UB和下界LB，允许误差ε>0，HP=∅，HR=∅，构造一个可行解x0。下面给出基于Benders分解的求解方法的详细步骤。

步骤1 将xk-1代入Benders子问题式(51)和式(52)中，该子问题为线性规划问题，求解结果可分为下述3种情况：

图2 基于Benders分解的求解方法流程图Fig.2 Flowchart of solution method based on Benders decomposition

a. 如果该子问题无可行解，算法终止；

c. 如果该子问题有最优值，则可以获得一个极点(ωp,ηp,χp)，利用该值更新上界UB=cTxk-1+(Pxk-1-p)Tωp-lTηp+(w-Wxk-1)Tχp，并执行下一步。

步骤2 将步骤1中获得的极点或极方向分别加入Benders主问题的约束条件HP和HR中，松弛型Benders主问题式(55)—(59)为混合整数线性规划问题，通过优化软件CPLEX求解可以获得最优解(xk,θk)，并计算下界LB=cTxk+θk。

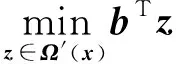
此外，文献[13]提出采用组合Benders割平面替代式(58)，即当xr使得Benders子问题无最优解时，在Benders主问题中加入下述整数型割平面:

(60)

该式的目的是通过改变xk的取值使得Benders子问题获得最优解。

4 算例仿真与分析

4.1 IEEE-RTS 26机测试系统

4.2 基于Benders分解的求解策略有效性分析

在MATLAB中调用CPLEX软件包编制相关程序对测试系统的主问题混合整数线性规划模型和子问题线性规划模型进行求解，其中子问题的求解结果情况可以根据求解函数的exitflag返回值判断。当对偶间隙取0.01%时，在主频2.4 GHz Intel CPU、8 GB 内存的PC上计算所需时间约为9.2 s。

为了验证本文基于Benders分解的两阶段迭代求解策略的有效性，表1给出了测试系统的每次迭代计算结果。从表中上下界的变化情况可以看出，总共迭代次数为5次，除第2次迭代获得的是极方向外，其他迭代获得的都是极值点。在迭代过程中不断修正原复杂问题的目标函数式(1)的上下界，即上界不断缩小，下界不断增大，最终逼近原问题的最优值。

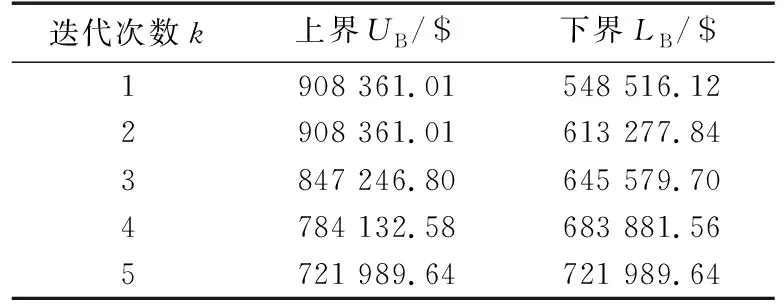
表1 测试系统的每次迭代计算结果Table 1 Iterative computation results of test system in each step

4.3 不同风储联合运行调度模式的比较分析

为了准确分析不同风储联合运行调度模式对系统运行结果的影响，首先给出4种算例：算例1为本文基于两阶段鲁棒区间优化的风储联合运行模式；算例2为基于两阶段鲁棒区间优化的风电场独立运行模式；算例3和算例4分别为基于确定性方法和随机规划方法的风储联合运行模式。假设算例4中的风电功率预测误差服从正态分布并覆盖区间范围。

以系统的基本运行成本和校正调度成本之和总调度成本作为经济评价指标。其中系统的基本运行成本即式(1)的系统发电成本，包括常规机组的出力成本、启停成本、备用成本、储能系统运行成本和弃风惩罚成本，通过对基于各算例相应优化方法的机组组合模型直接求解获得。校正调度成本是假设实际风电功率预测误差服从均匀分布，并对风电功率预测误差进行抽样获得风电实际出力场景，样本数为10 000，然后计算每个场景下的常规机组的实际出力，并针对系统安全约束无法保证的情况，通过采取校正调度措施，包括重新调整常规机组出力、释放备用容量、弃风和切负荷，恢复系统运行安全性而产生的调度成本。

系统的停电损失取为4 000 $/(MW·h)。算例1—4的系统运行的各类成本比较如表2所示。从表中算例1和算例2的各类成本比较可以看出，虽然储能系统与风电场配合运行会产生一定的储能系统运行成本，但系统运行的其他各类成本都相应减小，从而提高了系统整体运行的经济性。

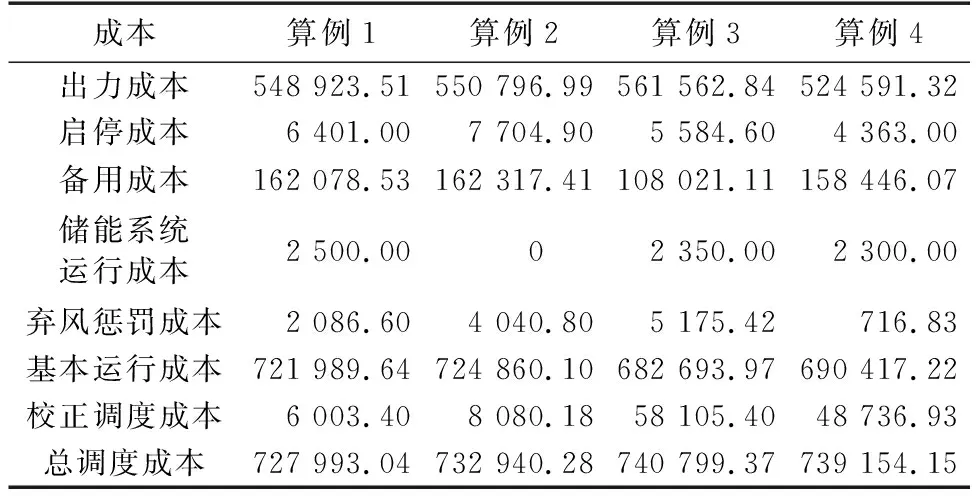
表2 算例1— 4的不同成本比较Table 2 Comparison of different costs among Case 1-4 $

图3 算例1中储能系统的放电、充电以及存储电量变化情况Fig.3 Variation of discharging/charging power and stored electricity of energy storage system in Case 1

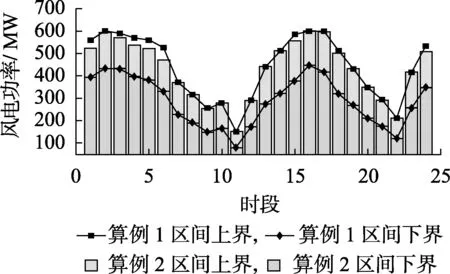
图4 算例1和2的风电允许出力区间上下界比较Fig.4 Comparison of allowable upper/lower bound of wind power output interval between Case 1 and 2

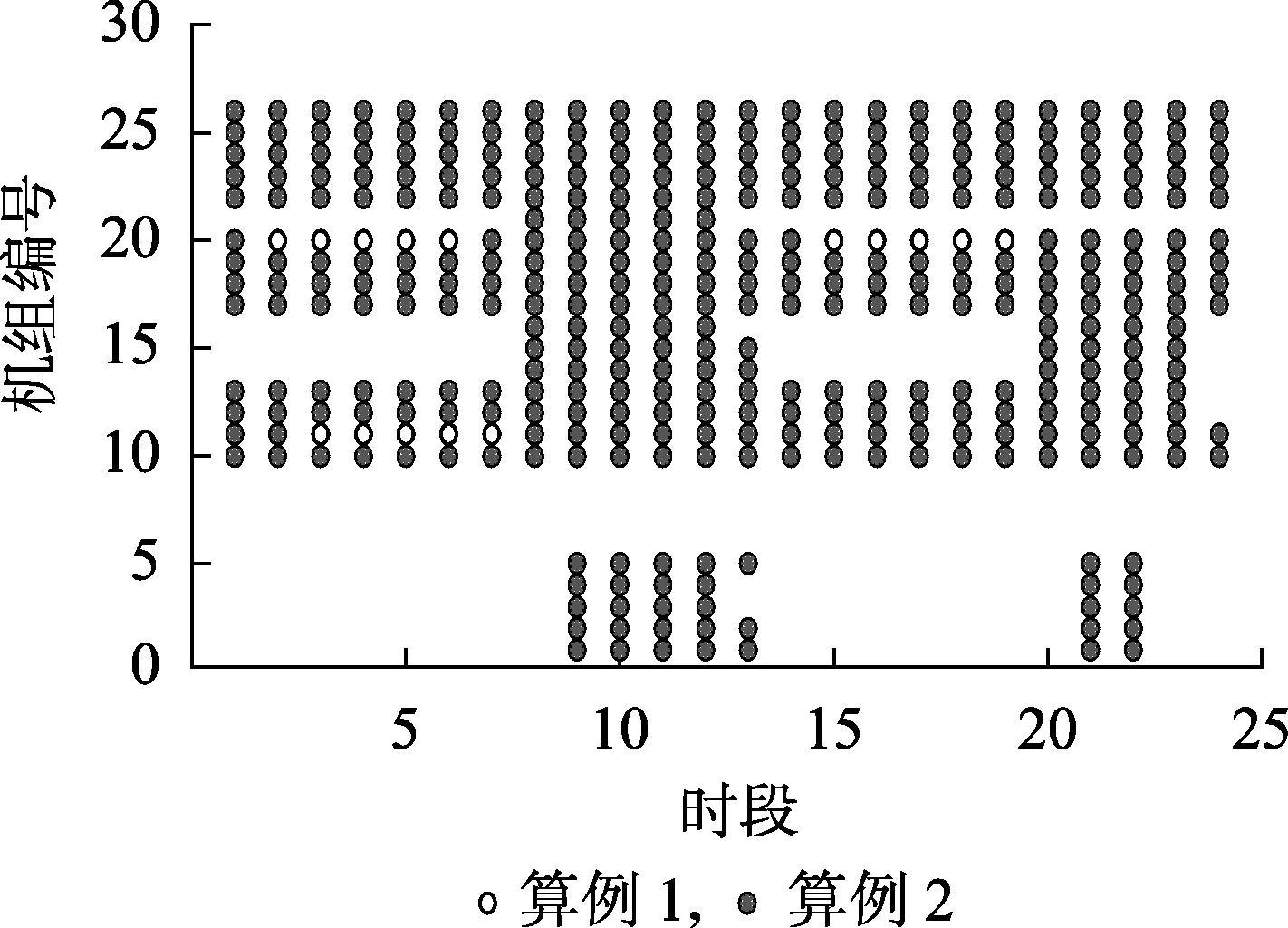
图5 算例1和2的常规机组运行状态比较Fig.5 Comparison of operation states of conventional units between Case 1 and 2

具体地，图3为算例1中储能系统的放电、充电以及储存电量变化情况。可以看出，虽然储能系统的充电容量大于放电容量，储能系统与风电场配合运行会有一定的电能损失，但是在负荷低谷、风电高发时段(第1—6、15—18时段)，储能系统充电，在负荷高峰、风电低发时段(第8—13、20—23时段)，储能系统放电，这使得负荷的峰谷差减小，从而增大了发电成本较低的机组在负荷低谷时段的出力，并减小了发电成本较高的机组在负荷高峰时段的出力，因此常规机组的出力成本减小。图4和图5分别为算例1和算例2的风电允许出力区间上下界以及常规机组组合比较，从图中可以看出储能系统通过在负荷低谷时段充电，增大了风电功率的消纳空间，并使得机组11和20在第3—6、15—18时段一直保持运行，减小了机组的启停成本，验证了风储联合运行的优越性。此外，算例1由于考虑的风电消纳空间增大，受风电不确定性的影响变小，较正调度成本也相对较小。

另外从表2中可以看出，与算例3和4相比，基于鲁棒区间优化方法的算例1和2的基本运行成本较大，主要原因是风电功率的不确定区间覆盖了风电功率预测误差场景，并且鲁棒区间优化方法要求机组组合优化决策在最极端风电出力场景下运行成本最低，这使得弃风功率、常规机组发电成本、储能系统运行成本都较大，从而使得系统基本运行成本最大。但在风电功率预测误差概率分布无法准确获取，例如本文均匀分布的极端情况下，相较于其他优化方法，算例3确定性方法的校正调度成本最大，而鲁棒区间优化方法的校正调度成本最小。具体原因分析如下：鲁棒优化方法能够使得在所有风电允许场景内，常规机组具备足够的调节容量以跟踪风电出力的变化，并且满足网络安全约束，因此，当风电功率预测误差服从不同概率分布时，鲁棒优化方法的校正调度成本最小；相比之下，其他优化方法受风电的不确定性影响较大，需要通过重新配置备用容量和切负荷措施来维持系统的安全运行，校正调度成本非常可观，其中确定性方法侧重调度方案的经济性，因而在调度方案的鲁棒性方面较差。在实际风电功率预测误差服从均匀分布的极端情况下，确定性方法的校正调度成本均远大于鲁棒区间优化方法，使得前者的总调度成本相对于其他方法均较大，而算例4的随机规划方法介于两者之间。

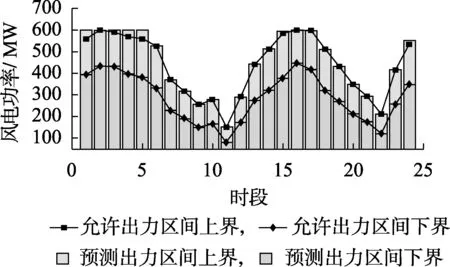
图6 算例1风电允许出力和预测出力的区间上下界比较Fig.6 Comparison of allowable and predicted upper/lower bound of wind power output interval in Case 1

可见在确定风储联合优化运行方式时，确定性方法和随机规划方法不适用于风电功率预测误差的概率特性刻画差异较大的场合。

此外，与基于现有鲁棒优化方法[7-9]的风储联合运行调度模型相比，本文提出的鲁棒区间调度模式能够计及系统旋转备用约束和网络安全约束对预测区间限制的影响，并能够从这2个方面约束考虑优化风电预测出力区间。图6为算例1风电允许出力和预测出力的区间上下界比较，从图中可以看出，在风电反调峰特性比较明显的情况下，算例1的风电允许出力区间仍小于风电预测出力区间，而此时采用现有鲁棒优化方法的风储联合运行调度模型会存在无解情况。

除储能系统外，利用需求侧响应资源参与电网调度可以进一步提升风电消纳水平[15]，因此未来需要在本文基础上，进一步研究考虑价格需求响应的鲁棒区间机组组合模型。

5 结论

本文利用风电功率预测的区间信息，提出了基于两阶段鲁棒区间优化的风储联合运行机组组合模型，并针对该模型中连续变量和离散变量间存在耦合关系导致计算过程中的对偶转换失效而难以求解的问题，提出了基于Benders分解算法的两阶段迭代求解策略。对含风电场和储能系统的IEEE-RTS 26机测试系统的蒙特卡洛仿真分析表明：在风电功率预测误差的概率特性刻画差异较大的场合，相对于确定性方法和随机规划方法，本文两阶段鲁棒区间优化方法在确定风储联合运行方式时能更全面地考虑风电不确定性对系统运行经济性和可靠性的影响；当风电渗透率较高且具有反调峰特性时，相对于现有鲁棒优化方法，本文模型能够从系统旋转备用约束和网络安全约束方面考虑，优化风电预测出力区间，综合优化风电消纳与储能系统运行。