变中思悟 探中明理——以苏教版五下《分数的基本性质》的教学设计为例

/朱国军 戴厚祥

小学数学的“分数”知识板块蕴含着丰富的数学思想，有助于培养学生的辩证思维。在教学苏教版五下《分数的基本性质》一课时，教师可以通过精心的教学设计，让学生经历分数基本性质的建构过程，归纳概括出分数的基本性质，运用分数的基本性质解决有关的数学问题。在此过程中培养学生观察、分析、比较、归纳、概括及动手实践的能力，发展学生的思维，让学生初步体会“变”与“不变”的辩证思想。本节课的教学设计以学生的探索活动为核心，寓数学思想方法于教与学的过程之中，以“变”与“不变”为主线，以“猜想—验证—观察—结论”的研究过程为暗线，让学生透过现象理解“商不变规律”“分数的基本性质”“比的基本性质”，体会其形不同而质同，感悟“变与不变”的辩证思想。

一、创设情境，引入分数

师（导入）：在“幸福嘉年华”寒假生活成果博览展销会上，点赞卡的数量是衡量学生表现的标准。在活动中，我统计了每组学生的参与人数和获赞人数，如表1。

表1 点赞卡统计表

师：从表格中的数量信息看，哪个小组表现得好？

生：从各组获赞比例看，各个小组表现都不错。

【设计意图】对信息的准确解读与理解，是生成新问题的必要基础。上课伊始，通过情境创设，以学生亲身经历的“幸福嘉年华”活动中的点赞卡引入，激发了学生探究新知的欲望，引发学生关注点赞人数与参与人数两个数量，让学生主动发现和应用分数。

二、自主探究，构建新知

1.猜测验证，形象感知。

学生汇报：

（1）折

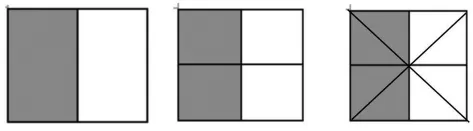
图1 学生的折纸方案

（2）转化

（3）摆

把8根小棒平均分成两份，取其中的一份是4根，把8根小棒平均分成四份，取其中的两份是4根，把8根小棒平均分成八份，取其中的四份也是4根。

（4）画

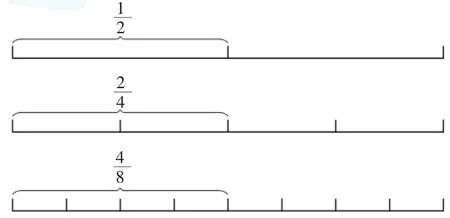
图2 学生所画线段图

【设计意图】引导学生用画一画、折一折、摆一摆、说一说等方法初步感受分数的“变与不变”，从而对其中的变化规律产生感性的、浅显的认识，渗透“数形结合”和“变中有不变”的数学思想方法。

2.想象列举，深入体验。

师：通过研究我们发现，分子分母不同，分数却相等。你还能从生活中找到像这样相等的分数吗？

生1：分西瓜。同样的西瓜平均分成4份取1份，和平均分成12份取3份是同样多的，他们的和是相等的。（如图3）

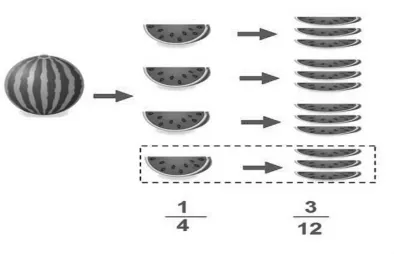
图3 平均分西瓜

生2：班级的座位分组。36人平均分成3组，其中的一组是12人；平均分成9组其中的3组也是12人；平均分成36份其中的12份也是12人，也就是

师（小结）：通过这两个例子，我们再次验证：分子分母变化，分数的大小可能不变。（板书：

【设计意图】通过任意举例再次验证，让学生的认知从单一具体现象发展为普遍规律，深刻感受分数的“变”与“不变”，为下一教学环节中由“变”到“不变”的转换奠定基础。

3.观察等式，探究规律。

师：比一比，看谁能在30秒内找出最多对相等的分数？

生3：其他组分数道理同上。

板书：分数的分子分母都乘或除以相同的数，分数的大小不变。

【设计意图】把分数教学的重点聚焦在学生的认知难点“分数的分子、分母怎么变，分数的大小才会不变”这个问题上，设计三次不同层次的探究活动：先创设情境引出一组相等分数让学生验证，再让学生从生活中找相等的分数并验证，最后让学生凭直觉快速写出相等的分数。分层次的教学设计，让学生由浅入深地理解分数的变化规律。

4.争论辨析，建构意义。

生（交流）：分子分母不能除以0，因为除数不能是0，乘0的话，分母就是0了，而分母不能为0，所以0除外。

师（小结）：分数的分子和分母同时乘或除以一个相同的数（0除外），分数的大小不变，这就是分数的基本性质。（板书：0除外：分数的基本性质）

课件演示：中国古代数学家刘徽在数学名著《九章算术》中对分数基本性质的研究。

【设计意图】在学生知晓“分数的分子分母同时乘或除以一个相同的数，分数的大小不变”这一规律后，出示特殊情况，引导学生主动质疑相同数0是否除外，使学生在质疑、释疑的过程中对规律有了进一步的理解，培养了他们的问题意识和严谨的数学学习态度。

三、拓展延伸，内化应用

出示习题：

3.选数：给定10个数，选出与某数相等的分数。

师：a与b之间的关系是什么？为什么存在这样的关系？你怎么知道的？

【设计意图】练习题的教学目的不能只停留在技能的掌握上，还应该关注学生的感悟、联想和提升。“写数”：通过在数轴上写相等的分数，感受“值同形不同的分数在数轴上的位置一样”的简约和极限思想；“改数”引导学生思考将异分母分数转化成同分母分数的规律，为以后学习约分、通分埋下伏笔，更便于分数大小比较、分数的加减运算；“填数”引导学生揭示（a、b是不为0的自然数）中a与b的倍数关系，既巩固了新知，又渗透了函数思想，有利于促进学生对数学的不断思索。

四、总结内容，提炼方法

师：毕达哥拉斯曾经说过：“在数学的天地里，重要的不是我们知道什么，而是怎么知道什么。”说说看，今天你知道了什么，又是怎么知道的呢？

学生交流后总结：

1.我们知道了分数的基本性质；

2.我们通过折一折、画一画、想一想发现了分数的基本性质；

3.我还知道了分数的基本性质和商不变的规律具有同样的性质……

师（总结）：我们在四年级认识了商不变的规律，今天我们又研究了分数的基本性质，到了六年级我们还会认识比的基本性质。在这样的学习中，变化的是学习内容，不变的是数学本质规律，许多数学知识都有着变与不变的表象，而我们都是在变与不变中寻求数学规律。

【设计意图】引导学生回顾所学知识和基本技能，反思学习过程，不仅交流知识技能方面的收获，还着重让学生分享学习方法、情感态度的体会，有助于学生内化、优化认知结构，感悟探究方法和数学思想，体验主动探究获取知识的愉悦，增强学习的动力和信心。