水位变化对近岸人工沙坝养滩效果影响的试验研究❋
拾 兵, 于 冬, 赵恩金, 赵多苍
(1.中国海洋大学工程学院,山东 青岛 266100; 2.中国铁建大桥工程局集团有限公司, 天津 300300)
水位变化对近岸人工沙坝养滩效果影响的试验研究❋
拾 兵1, 于 冬1, 赵恩金1, 赵多苍2
(1.中国海洋大学工程学院,山东 青岛 266100; 2.中国铁建大桥工程局集团有限公司, 天津 300300)
海滩侵蚀已经成为全球性的大问题,不仅引起了学术界广泛关注,也引起了民众的普遍关心。当前防护海滩侵蚀最有效的措施为海滩喂养,即人工补沙。本文采用极端高水位、设计高水位和0.00 m水位,进行近岸人工沙坝二维断面试验,研究不同水位下人工沙坝以及岸滩的变化,探究不同水位对人工补沙养滩防护效果的影响。试验结果表明:不同水位条件下,水位低时,人工沙坝顶部在形成的沙槽,随着水位升高,沙槽消失;岸滩受到波浪侵蚀区域向岸移动,侵蚀区域面积在扩大,岸滩的淤积区域也向岸移动。本文对所研究内容利用Flow-3D进行了数值模拟研究,其结果与物理试验吻合,可为近海补沙养滩工程提供理论依据。
水位;人工沙坝;岸滩;二维断面试验;数值模拟
日益严重的海滩侵蚀已引起全世界的关注,并成为海岸工程研究的热点课题。当前防护海滩侵蚀最有效的措施是海滩喂养,即进行滩肩补沙和沙坝补沙,并视海岸环境的特点辅以导堤促淤或外防波堤掩护。这种措施已为全球广泛应用[1]。
对于近岸沙坝补沙的研究,一般从理论研究、现场观测、物理试验和数值模型等四个方面进行。而国内外所进行的近海沙坝补沙试验研究,则一般研究水下沙坝对波浪折减效果,或者从研究近岸补沙对泥沙输移、沙坝移动和剖面演变等方面着手[2]。近年来,科研人员针对人工补沙,进行了很多试验研究,取得了丰硕的成果。Dette等[3]对宽与窄两组水下沙坝在相同波浪条件作用下进行水槽试验,研究其地形变化情况,结果显示,窄沙坝与宽沙坝相比,在沙坝高度减小方面速度较快、幅度较大,且有更多的泥沙向岸侧移动,而宽沙坝则有部分泥沙向海侧输移。Hoyng[4]通过试验对高位、低位两种近岸补沙方案进行了常浪及风暴浪下进行研究,结果表明近岸补沙在各工况下都降低离岸输沙,增强向岸输沙,人工补沙的高度对养护效果起到非常重要的影响。吴建等[5]通过进行二维物理断面试验,研究了近岸人工沙坝补沙对人工海滩波浪场、流场的影响,以及海滩剖面的演变。马悦等[6]利用Delft3D软件对极限波高作用下的沙坝变形与岸滩演变进行了数值模拟,将物理试验与数值模拟两种方法得到的地形结果进行了分析比较。杨燕雄等[7]以北戴河海滩的治理工程为背景,通过二维及三维模型试验研究了近岸人工沙坝补沙养滩工程中的参数设计和选取问题。赵多苍等[8]进行物理模型试验,开展了极限波高对近岸人工沙坝及岸滩演变的影响研究,探索了极端条件下人工沙坝达到动态稳定的条件。
而针对水位变化对近岸人工沙坝养滩效果影响方面研究则相对较少。因此,本文拟开展近岸人工沙坝对水位变化的响应研究,探索在不同水位下人工沙坝和岸滩的演变情况和对养滩效果的影响,并利用数值模型研究结果作为验证,为近海补沙养滩工程提供理论依据与技术支持。
1 理论分析
沙坝透射系数Kt为波浪越过人工沙坝时,坝后波高与坝前入射波高的比值:

(1)
式中:Ht为坝后透射波高;H为坝前入射波高。
透射系数为检验沙坝消减波浪能力的主要指标,透射系数愈小,沙坝的消浪效果愈好[9]。
波陡为波高与波长之比,见式(2),它表示波动的平均斜率[10]。当水位升高,波高、波陡会随之变化,故沙坝透射系数亦相应出现改变。

(2)
此外,随着水位的升高,初始岸线后的海滩会被淹没,水位增加会引起近岸海滩水下坡上移,坝顶水深加大。由此而引起水动力条件及波能增强,海洋动力环境会发生改变,即波浪场、潮流场和泥沙发生变化,故岸滩及沙坝剖面均会随之发生演变。受到近岸人工沙坝补沙的影响,初始剖面非均衡稳定的剖面,在水位升高的作用下,岸滩及沙坝剖面演变存在着复杂性。
本文采用极端高水位、设计高水位和0.00 m水位,对近岸人工沙坝及岸滩进行二维断面试验,分析波陡参数对沙坝透射系数的影响,研究不同水位下人工沙坝以及岸滩的变化,探究不同水位对人工沙坝补沙养滩防护效果的影响。
2 物理模型试验
2.1 试验条件
二维物理模型试验在山东省海洋工程重点实验室波浪水槽中进行,波浪水槽的尺寸为:长60.0 m、宽3.0 m、深2.0 m。波浪水槽的造波系统由波流水槽、造波控制系统、水槽前端的推板式造波机和水槽末端的多孔介质消能措施4部分组成。
波高测量采用天津水运工程科学研究院所生产的SG2000型波高仪。海床高程采用激光全站仪进行测量,精度为1 mm。试验岸滩剖面通过野外调查和观测确定的典型剖面,试验横断面长600 m,试验断面布置如图1所示。根据模型布置,离岸距离112 m处为1号波高仪,测量浅水波高;离岸距离217 m处为2号波高仪,测量坝后波高;离岸距离290 m处为3号波高仪,测量坝前波高;离岸距离402 m处为4号波高仪,测量深水波高,这样可以测量垂直岸线沿程有代表性的波高值,继而可得到沿程波高的变化情况,通过2号、3号所得数据也可计算沙坝透射系数。

图1 试验断面示意图Fig.1 Sketch of the experiment section
2.2 试验比尺
本断面试验是为了研究不同水位条件下人工沙坝及岸滩与波浪之间的相互作用,根据相似理论,重力是主要作用力,模型试验相似应首先满足重力相似[10]。采用几何比尺λl=10的正态波浪模型,模型比尺按表1选取。

表1 模型比尺Table 1 Model scale
2.3 试验参数
2.3.1 试验水位及波浪参数 试验采用0.00、1.35 m(设计高水位)和2.66 m(极端高水位)3种水位(黄海高程)作为代表水位,进行潮位控制。试验采用规则波,在距离岸边400 m为外海开边界的入射动力条件,各工况波高为3种水位对应的规则波极限波高。3种水位对应的极限波高、波浪周期和波长参数数值见表2。

表2 3种水位对应的极限波高、波浪周期和波长数值Table 2 Extreme wave height, wave period, and wave length with three different water levels
2.3.2 泥沙参数 岸滩位置处的模型沙中值粒径为0.06 mm,对应原型沙粒径为0.60 mm的天然沙。人工沙坝处模型沙中值粒径为0.15 mm,对应原型沙粒径为1.5 mm的中粗沙。
2.3.3 试验工况 本模型试验研究人工沙坝设计参数中,离岸距离、沙坝高程和坝顶宽度等保持不变,而水位及其引起的入射波等条件变化时,对人工沙坝消弱波浪、养护海滩及自身演变的影响。人工沙坝设计为潜坝(有一定的过水能力),坝顶高程设计为-0.9 m,坝顶宽度为30 m,离岸距离250 m。在人工沙坝迎水坡处较陡,波浪会发生破碎,破碎波类型为卷破波,波峰的前沿面首先变成直立面,随即向前呈卷舌状,最后卷舌没入到波谷中。卷破波水体有较大范围的紊动与回流,容易产生沙坝泥沙输移。根据试验目的,试验方案设计组次如表3所示。

表3 试验工况Table 3 Experiment cases
3 试验结果及分析
3.1 不同水位下波高沿程变化
图2为不同水位时波高沿着离岸距离的变化图。其中,离岸距离112 m处波高H1对应1号波高仪数据;离岸距离217 m处是沙坝后波高H2,对应2号波高仪数据;离岸距离为290 m处是沙坝前波高H3,对应3号波高仪数据;离岸距离402 m处波高H4对应4号波高仪数据;离岸距离为250 m处是沙坝坝顶波高。

图2 不同水位时波高沿程变化Fig.2 The changes of wave height along distance with different water levels
从图中可以看到:波浪在向岸滩传播过程中,波高一直在衰减,在波浪越过人工沙坝时,波高下降趋势尤为明显,说明人工沙坝有比较好的消减波浪效果。
由图2中曲线亦可得到:不同水位条件下,波高沿程变化曲线斜率有所不同。在水位较低时,人工沙坝前后位置处波高变化曲线斜率明显较大;而在水位较高时,在相同位置,波高变化曲线斜率不大。原因在于试验各工况中,人工沙坝高程为定值,当水位较低时,坝顶水深较小,限制了波浪的传播,波高可能在人工沙坝斜坡处或坝顶位置发生破碎,波高则减小;而当水位较高时,坝顶水深较大,大于波浪破碎水深,波浪越过人工沙坝时没有发生破碎,波高衰减不明显。对比结果中坝顶处波高与沙坝前波高之比,通过计算可知,当水位分别为0.0、1.35和2.66 m时,二者比值为0.497、0.803及0.895。通过以上数据可以说明前述原因正确。
3.2 波陡对透射系数的影响
表4为3种水位对应组次4、5、6中波浪的透射系数的变化值。由表可知:随着水位的升高,对应的波浪参数随之变化,透射系数亦逐渐增大。
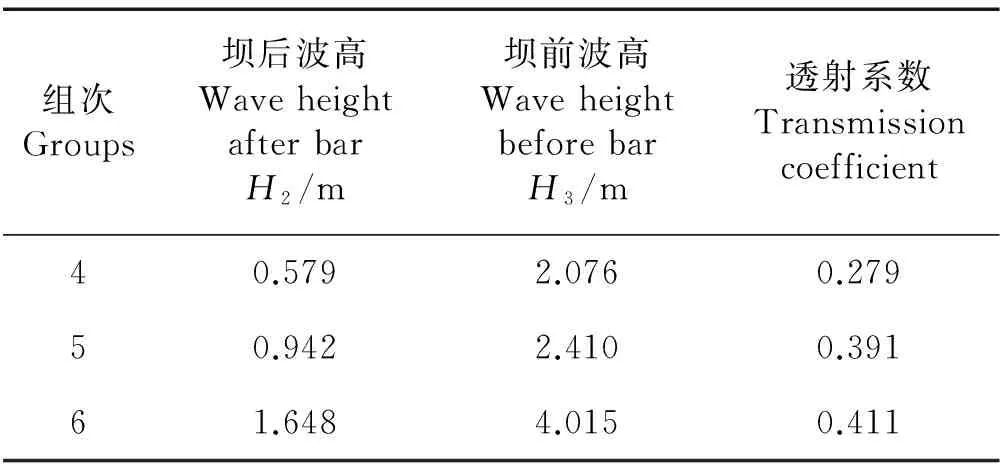
表4 三种水位对应的波浪透射系数Table 4 Wave transmission coefficients with the three different water levels
图3是当沙坝高程为-0.9 m时,波浪透射系数与入射波波陡之间关系曲线。
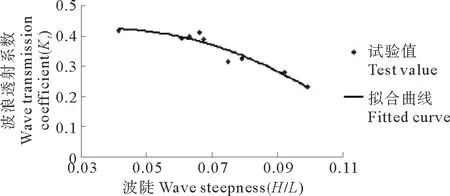
图3 波浪透射系数与波陡的关系曲线Fig.3 Relation curve between wave transmission coefficient and wave steepness
从图3可以看到波浪透射系数随着入射波波陡的增大而减小。在有限振幅波理论中,波浪进入浅水区后,极限坡陡不是常数,它与相对水深有关,根据有限水深的极限坡陡公式[10]:

(3)
拟合波陡与透射系数之间的关系曲线,可得:

(4)
式中:Kt为透射系数;H为坝前入射波波高;L为坝前入射波波长;H/L为波陡。拟合曲线与实测数据的相关系数为0.85。
当波陡达到此值时,波浪将发生破碎。因此,波浪越过沙坝时,相同坝顶水深,波陡越大,波浪越容易达到破碎条件,由于破碎造成的波能量大量耗损,从而使人工沙坝的消浪作用加大,波浪透射系数减小明显。
3.3 水位不同对沙坝变形的影响
图4为不同水位工况下沙坝剖面演变图,对应的是沙坝高程为-0.9 m中的3种工况。

图4 不同水位工况沙坝剖面图Fig.4 The profiles of sand bar with different water levels
由图4可知,0.00 m水位时,可观察到人工沙坝剖面顶部有比较明显的沙槽出现;而在设计高水位、极端高水位两种工况下,没有观测到人工沙坝剖面顶部有比较明显的沙槽出现。
分析可知:不同水位条件下,水位低时,人工沙坝顶部在形成的沙槽,随着水位升高,沙槽消失。出现此现象的原因在于:试验中沙坝高程为-0.9 m,高度较低,而水位又比较高,沙坝顶部有一定的过水能力。当水位很大时,沙坝坝顶水深大于波浪破碎临界水位,入射波在坝顶上方尚未发生波浪破碎,故而未形成沙槽。
此外,与初始放置的人工沙坝比较而言,波浪作用后,沙坝背水面坡角变陡,迎水面坡角变得平缓,但随着水位的逐渐上升,迎水面坡角逐渐变陡。
3.4 水位不同对岸滩变形的影响
图5是不同水位工况的岸滩演变图,对应的是沙坝高程为-0.9 m中的3种工况。

图5 不同水位工况的岸滩剖面图Fig.5 The profiles of beach with different water levels
由图5可知:不同水位工况时,各水位对应的岸滩侵蚀区域与淤积区域也各异,具体见表5,表中距离均为离岸距离。
分析可知:不同水位工况下,随着水位的升高,岸滩受到波浪侵蚀区域向岸移动,侵蚀区域面积扩大;随着水位的升高,岸滩的淤积区域也向岸移动。究其原因,水位升高会直接淹没海滨而引起海岸线后退,不仅如此,还引起近岸海洋水动力加强,越滩波浪增多,破坏岸滩的平衡稳定而造成海滩侵蚀、岸线退却[10]。

表5 3种水位对应的侵蚀与淤积区域Table 5 Erosion and deposition areas with three different water levels
从长期看,此结论与Bruun模型所揭示的规律一致,即随着海平面的上升,海滩平衡剖面向上部与向陆移动[12-13](见图6)。只是短期内受人工沙坝补沙的影响,水位上升后,岸滩侵蚀、岸线后退效果没有理论上的明显。

图6 Bruun模型示意图(1962年)Fig.6 Sketch according to the Bruun Model (1962)
4 数值模拟
4.1 控制方程
本文主要应用的是FLOW-3D软件其中的VOF模型及两相流(泥沙与水流)进行数值模拟研究,入口为波浪边界,出口为自由出流边界。
本文所建立的数值波浪水槽要模拟波浪与沙坝的相互作用,波浪是不可压缩粘性流体的运动,FLOW-3D将连续性方程和不可压缩粘性流体运动的Navier-Stokes方程作为流体运动的控制方程。波浪会出现剧烈的变形破碎,适合采用RNGk-ε模型进行模拟。
连续性方程:

(5)
动量方程式

(6)

(7)

(8)
其中:ρ为流体密度;VF是可流动的体积分数;Ax、Ay、Az代表着x、y、z3个方向可流动的面积分数;u、v、w为对应x、y、z的速度分量;Gx、Gy、Gz为物体在x、y、z3个方向的重力加速度;fx、fy、fz为3个方向的黏滞力加速度。
泥沙模型中悬沙的对流扩散方程为
(9)
其中:Cs为悬沙浓度;Lj为泥沙通量;Dj为沉降项。
4.2 数值模型波浪水槽
为与试验结果进行对照,本文采用的模拟区域与试验模型尺寸相同。数值模型地形图如图7所示,计算区域为长宽高为:40.0 m×15.5 m×1.0 m。Xmin为线性波浪边界条件,Xmax为自由出流边界条件,Zmin为壁面边界条件,Ymin、Ymax、Zmax均为对称边界条件。

图7 模型地形示意图Fig.7 Terrain sketch of the model
4.3模型验证
以模型试验中离岸距离为400 m处3种入射波高数据为基础,对数模波浪进行验证。从图8、9、10中可以看出,波浪试验值与数模值相吻合较好。

图8 2.34 m波高验证图Fig.8 Verifications of wave height 2.34 m

图9 3.00 m波高验证图Fig.9 Verifications of wave height 3.00 m

图10 4.40 m波高验证图Fig.10 Verifications of wave height 4.40 m
4.4 结果对比
为证明试验结果的有效性,本文将数值模型沿程波高、沙坝变形及岸滩变形结果与试验结果对比。图11为各水位下沿程波高对比图。图12水位为1.35 m、波高3.00 m情况下沙坝演变对比图。图12为水位为1.35 m、波高3.00 m情况下岸滩演变对比图。
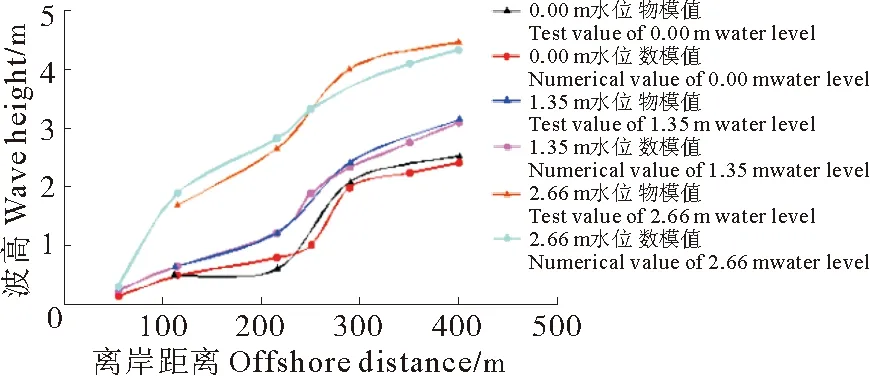
图11 波高对比图Fig.11 Comparison of wave height
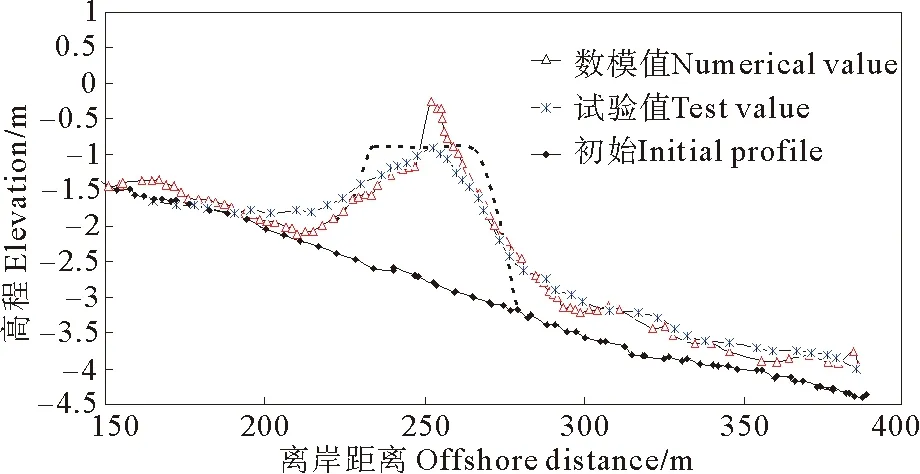
图12 沙坝对比图Fig.12 Comparison of sand bar

图13 岸滩对比图Fig.13 Comparison of beach
由以上图可知,数值模型结果与物理模型结果曲线规律相吻合,证明试验结果有效,可用于指导工程实践,为工程应用提供理论支持与科学依据。
5 结论
本文通过对3种不同水位下近海人工沙坝养滩二维物理模型试验研究,并通过数值模型验证,得出以下结论:
(1) 波浪在沿着离岸距离向岸滩传播中,波高一直在减小,在波浪越过人工沙坝时,波高下降趋势尤为明显,这说明人工沙坝有较好的消减波浪效果;
(2) 波浪越过沙坝时,相同坝顶水深,波陡越大,波浪越容易达到破碎条件,由于破碎造成的波能大量耗损,从而使人工沙坝的消浪作用加大,波浪透射系数减小;
(3) 不同水位条件下,水位低时,人工沙坝顶部在形成的沙槽,随着水位升高,沙槽消失;
(4) 不同水位工况下,随着水位的升高,岸滩受到波浪侵蚀区域向岸移动,侵蚀区域面积扩大,岸滩的淤积区域也向岸移动。
6 进一步研究的探讨
(1) 由于本试验中波高仪数量及其布置位置的局限,无法测量在岸滩处(离岸距离小于110 m)波高详细变化情况,因此不能精确地研究此区域波高的变化对岸滩的地形塑造的影响,下一步需要优化试验方案,以期使研究数据丰富,结果更加完善。
(2) 本试验中离岸距离、沙坝高程和坝顶宽度等保持不变,而水位及其引起的入射波等条件变化时,对人工沙坝消弱波浪、养护海滩及自身变形的影响。试验工况需要增加,包括改变沙坝高程、坝顶宽度和沙坝离岸距离等,这样可以系统地研究水位对人工沙坝补沙养滩效果的影响。
[1] 王颖, 吴小根. 海平面上升与海滩侵蚀[J]. 地理学报, 1995, 50(2): 118-127.
Wang Y, Wu X G. Sea level rise and beach response[J]. Acta Geographica Sinica, 1995, 50(2): 118-127.
[2] 吴建, 拾兵. 近岸补沙养护海滩研究综述[J]. 海洋科学, 2011, 35(8): 108-112.
Wu J, Shi B. A review of the shoreface nourishment for beach protection[J]. Marine Sciences, 2011, 35(8): 108-112.
[3] Dette H H, Larson M, Murphy J, et al. Application of prototype flume tests for beach nourishment assessment[J]. Coastal Engineering, 2002, 47: 137-177.
[4] Hoyng C W. Erosive and Accretive Coastal Profile Response[D]. Delft: Delft University of Technology, 2008.
[5] 吴建, 拾兵, 李智, 等. 近岸人工沙坝保滩促淤的试验研究[J]. 海洋通报, 2012, 31(2): 176-180.
Wu J, Shi B, Li Z, et al. Experimental study on the shore nourishment for beach protection and siltation promotion[J]. Marine Science Bulletin, 2012, 31(2): 176-180.
[6] 马悦, 拾兵, 杨燕雄, 等. 近海人工沙坝护岸养滩的模拟方法[J]. 海洋地质前沿, 2013, 29(2): 31-36.
Ma Y, Shi B, Yang Y X, et al. Simulation methods for artificial nearshore sanbars for costal protection and beach nourishment[J]. Marine Geology Frontiers, 2013, 29(2): 31-36.
[7] 杨燕雄, 杨雯, 邱若峰, 等. 人工近岸沙坝在海滩养护中的应用-以北戴河养滩工程为例[J]. 海洋地质前沿, 2013, 29(2): 23-30.
Yang Y X, Yang W, Qiu R F, et al. Application of artificial submerged sandbars to beach nourishment—a case from Beidaihe beach[J].Marine Geology Frontiers, 2013, 29(2): 23-30.
[8] 赵多苍, 拾兵, 宋朋远, 等. 极限波高下人工沙坝的动力调整研究[J].中国海洋大学学报: 自然科学版, 2014, 44(6): 97-102.
Zhao D C, Shi B, Song P Y, et al. Study of Artificial Sand Bar Dynamic Adjustment on Limit Wave Height[J]. Periodical of Ocean University of China: Natural Science Edition, 2014, 44(6): 97-102.
[9] 赵多苍. 沙质海滩侵蚀与近岸沙坝防护技术研究[D].青岛: 中国海洋大学, 2014.42-45.
Zhao D C. Study on Sandy Beach Erosion and Protection Technology for the Offshore Artificial Sand Bar[D]. Qingdao: Ocean University of China, 2014.42-45.
[10] 邹志利. 海岸动力学[M]. 北京: 人民交通出版社, 2009.77-81.
Zou Z L. Coast Dynamics[M]. Beijing: China Communications Press, 2009.77-81.
[11] 严恺. 海岸工程[M]. 北京: 海洋出版社, 2002.570-598.
Yan K. Coastal Engineering[M]. Beijing: China Ocean Press, 2002.570-598.
[12] Bruun P. Sea-level rise as a cause of shore erosion[J]. Journal Waterways and Harbors Division, 1962, 88: 117-130.
[13] Bruun P. The Bruun rule of erosion by sea-level rise: A discussion of large-scale two-and-three-dimensional usages[J]. Journal of Coastal Research, 1988, 4(4): 627-648.
责任编辑 陈呈超
ExperimentalStudyonEffectofBeachNourishmentwiththeOffshoreArtificialSandyBarResponsetoWaterLevelChange
SHI Bing1,YU Dong1,ZHAO En-Jin1,ZHAO Duo-Cang2
(1. College of Engineering, Ocean University of China, Qingdao 266100, China; 2. China Railway Construction Bridge Engineering Bureau Groups Co Ltd, Tianjin 300300, China)
Beach erosion has become a major global problem, which not only causes Widespread attention from academia, but also causes widespread concern from people. At the present time, the most effective protection measures of beach erosion is beach nourishment, namely artificial sand filling. In this paper, two-dimensional sectional experiment of the offshore artificial sand bar was conducted with three different water levels, which were extreme high water level(2.66m), design high water level(1.35 m) and 0.00 m water level, respectively. This experiment was designed to study the change of artificial sand bar and beach, and explores the effect of beach nourishment protection under the condition of the three different water level. The result shows that: Under the case of different water levels, when water level was low, sand tanks produced on the top of artificial sand bar; with water level increasing, sand tanks disappeared. Erosion areas of beach under the wave action condition were closer to shore and become larger. Deposition areas of beach were closer to shore too. In this paper, Flow-3D was also used to carry out numerical simulation for the research content, which results were consistent with the two-dimensional sectional experiment. The study could provide a theoretical basis for the offshore filling sand beach nourishment project.
water level; artificial sand bar; beach; two-dimensional sectional experiment; numerical simulation
P753
A
1672-5174(2018)01-104-07
10.16441/j.cnki.hdxb.20150221
拾兵, 于冬, 赵恩金, 等. 水位变化对近岸人工沙坝养滩效果影响的试验研究[J]. 中国海洋大学学报(自然科学版), 2018, 48(1): 104-110.
SHI Bing, YU Dong, ZHAO En-Jin, et al. Experimental study on effect of beach nourishment with the offshore artificial sandy bar response to water level change[J].Periodical of Ocean University of China, 2018, 48(1): 104-110.
国家自然科学基金项目(51279189)资助
Supported by the National Natural Science Foundation of China(51279189)
2015-06-22;
2016-01-28
拾 兵(1961-),教授,博导,主要从事河流、河口与海岸动力学研究。E-mail:sediment@ouc.edu.cn

