基于CMIP3与CMIP5模式对北太平洋大气环流模态的评估分析❋

陈 峥， 甘波澜， 吴立新

(1.中国海洋大学物理海洋教育部重点实验室，山东 青岛 266003； 2.青岛海洋科学与技术国家实验室， 山东 青岛 266200)

基于CMIP3与CMIP5模式对北太平洋大气环流模态的评估分析❋

陈 峥1,2， 甘波澜1,2， 吴立新1,2

(1.中国海洋大学物理海洋教育部重点实验室，山东 青岛 266003； 2.青岛海洋科学与技术国家实验室， 山东 青岛 266200)

以美国国家海洋和大气局-环境科学协作研究所(NOAA-CIRES)二十世纪大气再分析数据集第二套c版(Twentieth-Century Reanalysis Dataset Version 2c；20CR V2c)资料所提取的二十世纪北太平洋大气环流模态作为观测参考值，利用泰勒图方法与谱分析方法，分别对太平洋北美型遥相关(Pacific-North America Teleconnection; PNA)与北太平洋涛动(North Pacific Oscillation; NPO)模态在国际耦合模式比较计划第三阶段(Coupled Model Intercomparison Project Phase 3；CMIP3)与CMIP5两套多模式数据集合中的表现进行了从空间型到时间周期的综合评估与对比分析工作，并对PNA的4个异常中心以及NPO的2个偶极子进行简化命名。评估结果表明：整体上CMIP5模式对PNA与NPO的空间型模拟能力要优于CMIP3模式，80%的CMIP5模式都能很好的体现与观测PNA/NPO模态相近的空间分布与振幅，而CMIP3模式只能达到约60%。在模式模拟优秀率上，CMIP5也远高CMIP3约10%。在使用谱分析方法对两套资料对时间模拟能力评估结果表明：CMIP5相比于CMIP3并没有太大的进步，整体合格率与CMIP3持平。其中大部分模式能够很好的模拟出同观测一致的PNA 1～2年和4～6年的年际周期，对其20～25年的年代际周期的模拟相对较差；而对NPO来说，更多模式的功率峰值都在1～2年周期上，而且只有约一半模式能够体现与观测相同的2～4年周期。

太平洋-北美型遥相关(PNA)；北太平洋涛动(NPO)；泰勒图；谱分析

现有研究表明，联合国政府间气候变化专门委员会(Intergovernmental Panel on Climate Change；IPCC)多模式在大尺度范围内对于区域和全球气候变化具有较强的模拟能力并能够很好地模拟各个气候要素，模式的不断发展与完善，也在一定程度上降低了气候预测的不确定性。全球气候模式是气候变化预估与机理研究的重要工具，但由于全球气候系统的复杂性、气候模式的可靠性与代表性等因素，模式对气候变化的模拟能力仍然存在一些不足之处，并且模式本身的系统性误差仍是不可避免的，而且由于模式在初始条件与参数化方案设置、空间分辨率以及机理等方面的差异，会导致不同模式间的模拟结果存在较大差异，这在一定程度上会影响气候预测及预估水平[1-2]。

现如今，开展气候变化预估与机理研究主要依赖全球气候系统模式，通过数值模式构建地球大气环境，模拟人类的生活环境，在模式能够较为准确的模拟地球目前大气环境的基础上，通过改变模式参数(如温室气体浓度等)，以达到对未来气候变化预估目的。其中准确且合理的模拟历史气候是预估报未来气候变化的基础，从而解决人类可持续性发展的根本问题。而模式评估本身也是开展气候模拟、趋势预测与预估的基础性工作，也是深入了解模式所存在不足的重要途径，有利于对气候变化影响、适应和减缓等方面的研究，其中，对大气低频变率主模态的模拟为模式评估的重点对象[3-4]。

太平洋-北美型遥相关(Pacific-North America teleconnection；PNA)与北太平洋涛动(North Pacific Oscillation；NPO)在冬季北太平洋大气环流模态中占据主导地位，并且与亚太急流和太平洋风暴轴的位置与强度有密切联系，同时对北美水文气候有重要影响。正位相的PNA与西风急流的增强以及向东延伸有关，而急流的北移以及其出口区的扩张则与正位相的NPO有关[5-6]。在涡旋平均流相互作用的框架下，PNA与NPO都对与流速异常的风暴轴变化具有调制作用，如风暴轴活动的纬向移动和下降流增强等都与其有关[6-8]。研究表明，这些大气动力变化都对北美的气候具有重要影响，尤其在冬季[9-10]，如PNA与北太平洋阻塞频率[11]、北美降雪厚度[12]以及美国北部与中部地区的降水[13]有关，而NPO与冬季北美西部地区和白令海西部冰雪圈的气温与降水有关[5]。此外，PNA在阿留申低压处的负异常信号与太平洋年代际振荡(Pacific Decadal Oscillation；PDO)[3,14]有关，而NPO则为驱动北太平洋回旋振荡(North Pacific Gyre Oscillation；NPGO)的大气外强迫[4,15]。

PNA与NPO作为北太平洋大气环流主模态，对环太平洋区域气候变率具有深远影响，与人类所生存的气候条件息息相关，因此有必要评估IPCC多模式对其模拟的能力。本文创新之处在于，之前从未有人使用IPCC两次评估报告所评估的两套国际耦合模式比较计划(Coupled Model Intercomparison Project；CMIP)多模式数据集(CMIP3与CMIP5)进行对PNA/NPO空间型与时间周期的模拟能力的综合评估与对比分析工作，因此本文的评估与分析是必要并且具备实际应用价值的。对比评估可以反应出IPCC两套多模式数据集合模拟能力的异同，比较结果对改进模式有极为重要的启示意义。

1 研究背景

PNA与NPO是冬季北太平洋区域变化的主要大气环流结构，是具有行星尺度的大气异常模态，是对流层中上层、海平面气压层上大气环流变化最显著的模态，其演变不仅直接影响北太平洋附近地区的天气和气候，甚至对整个北半球的大气环流异常及气候突变都有重要影响。

PNA是北半球中纬度变化的主要环流结构之一，是北太平洋对流层中上层大气环流变化最显著的模态，涉及了北太平洋和北美大陆区域大气环流的异常状态，具有4个异常活动中心。以正位相为例：其中2个为正异常结构分别位于夏威夷群岛(20°N, 160°W)与加拿大亚伯达(55°N, 115°W)，以及2个负异常结构分别位于阿留申群岛南部海区(45°N, 165°W)和美国墨西哥湾岸区(30°N, 85°W)；反之为 PNA 的负位相[16]。对于 PNA 的空间结构，人们常采用经验正交函数(EOF)分解的方法来得到。对冬季北半球 500 hPa位势高度异常场进行EOF分解后，第一模态的空间分布可以看做是PNA型遥相关。此外，正负位相的PNA模态所分别对应的地表气温和降水异常，对研究环太平洋地区冬季旱涝灾害，以及暖冬冷冬的预测，具有重要意义。

NPO是在北太平洋海区经向上的具有2个海平面气压异常中心的偶极子，以正位相为例，正异常结构位于副热带夏威夷群岛附近，负异常位于阿拉斯加附近[17]，是北半球大气中一个显著经向的跷跷板式的低频振荡模态。Linkin和Nigam[5]指出，NPO在海平面气压场的异常信号在对流层中表现为西太平洋型遥相关(West Pacific Teleconnection；WP)[16]，为500 hPa位势高度场中位于PNA之后的第二主模态。研究发现，当北太平洋涛动增强时，活动中心之间的气压差增大，阿留申低压较常年偏东，夏威夷高压偏西；当北太平洋涛动弱时，活动中心之间的气压差减小，阿留申低压则较常年偏西，夏威夷高压偏东。

根据PNA与NPO对北太与北美的水文气候的影响，作者认为对这两个模态在IPCC多模式二十世纪的模拟中进行综合评估十分必要。但至今为止，相关评估工作还不完善，如Stoner等[1]评估了CMIP3模式对PNA对模拟情况，发现大部分模式在冬季能够抓住似PNA型的模态，但是高估了PNA在位势高度异常上的方差贡献率，并且忽略了对PNA周期的评估。Furtado等[2]使用CMIP3中20C3M与A1B情景，发现NPO与NPGO型海表温度异常有关，但在全球变暖后空间型并无太大改变。而在IPCC第五次评估报告中所评估的CMIP5模式中，对PNA与NPO的模拟能力的评估工作尚不完整[18]。这也是本文进行CMIP3/CMIP5模式在二十世纪情景下对PNA/NPO的模拟能力进行综合评估与对比分析工作的动力之所在。

2 数据与方法

2.1 观测数据

本文作为观测资料所采用的研究数据主要包括：位势高度场(GPH)和海表面气压场(SLP)，数据均来自美国国家海洋和大气局-环境科学协作研究所(NOAA-CIRES)二十世纪大气再分析数据集第二套c版(Twentieth-Century Reanalysis Dataset Version 2c；20CR V2c)[19-20]。20CR V2c是目前国际上最新发展的一套具有创新性、综合性的二十世纪全球大气环流再分析数据集，该数据集与观测模式相结合，可提供一套极为全面的气候描述与分析。本文使用整个二十世纪的月平均数据，并将2°×2°网格差值到2.5°×2.5°网格，其中GPH场取500 hPa层。

本文选取此数据集作为观测资料是因为20CR V2c中二十世纪中后期数据资料与其它大气再分析数据(如ECMWF、NCEP/NCAR资料等)相比，结果表明20CR V2c具有较高的数据质量，并且对北太平洋区域太平洋-北美型遥相关和北太平洋涛动的变率和趋势评估具有较高可信度[19-23]。

2.2 模式数据

本文采用IPCC第四次评估报告(Forth Assessment Report，即AR4)中所评估的22个CMIP3全球海气耦合模式的数值试验输出资料[24]；以及采用IPCC第五次评估报告(AR5)中所评估的隶属于气候模型诊断与比对项目(Program for Climate Model Diagnosis and Intercomparison；PCMDI)的35个CMIP5模式资料[25]；使用两套IPCC多模式所输出的GPH与SLP场分别研究各模式对二十世纪PNA与NPO的地理分布与时间周期的模拟结果；将各模式资料全部差值到2.5°×2.5°网格以便于比较。对于CMIP3(CMIP5)多模式，本文选取其对二十世纪模拟情景20C3M(Historical)进行评估分析，该情景使用二十世纪观测资料的人为与自然变率对大气的影响作为外强迫，此试验中温室气体(二氧化碳)浓度为观测值，该情景除了考虑了太阳常数和温室气体的影响外，还考虑了火山爆发、硫化物、臭氧、碳循环和气溶胶等对气候变化的影响，作者使用同观测一致的1900—1999年作为实验研究的时间长度。本文所采用的22(35)个CMIP3(CMIP5)模式均选取“run1”(“r1i1p1”)运行结果，各模式名称参考泰勒图例见(见图3～图6)。

2.3 主要方法介绍

2.3.1 北太平洋大气环流主模态的获取 针对PNA(NPO)模态，本文主要使用500 hPa GPH场(SLP场)进行提取，使用范围为10N°～80°N，150°E～60°W(10N°～80°N，120°E～60°W)的区域，使用EOF及回归等方法进行分析处理各模式的冬季资料。本文采用的获取模态的具体方法如下：

(1)将500 hPa GPH场(SLP场)进行去趋势以及去除逐月气候态处理以得到异常场GPHa(SLPa)。

(2)将GPHa(SLPa)进行3个月的滑动平均以达到低通滤波的目的，并从中取出12、1和2(DJF)组成一个新的连续冬季场。

(3)再将冬季场乘以纬度权重后进行时空变换，将三维场变为时间-空间二维场之后进行EOF分解，得到其特征向量所表征PNA(NPO)正位相所对应的第一(二)主成分PC1(PC2)。

(4)将PC1(PC2)进行标准化处理，再将步骤2中的冬季异常场回归到标准化序列上，从而最终得到PNA(NPO)空间模态，单位：m(hPa)。

2.3.2 泰勒图分析方法 泰勒图[26]能够将多模式的相关信息集中表示，是近年来被广泛采用的应用于模式评估与检验的有效方法，能够将多个变量的标准差、与参考值的相关系数以及均方根偏差综合显示在一张二维图上。在泰勒图中，可以将多个模式的相关信息集中表示，全面清晰地反映多模式的模拟能力。标准差反映多变量自身的离散程度，相关系数表示变量值与参考值的相似性，均方根误差表示变量与参考值之间的离散度，均方根误差值越小，表明与参考值自身的离散程度越接近。

下面具体来说泰勒图的三个组成部分：

(1)标准差公式(σ)：

(1)

上式：标准差为σ；N个变量x，其平均值为μ。标准差为一组数据与其平均值的分散程度，标准差越小，代表这些数值越接近平均值。

(2)相关系数(R)：

假设参考值(Reference)f与变量m，其相关系数R表达式为：

(2)

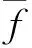
(3)均方根误差(E)：

假设参考值f变量m，其均方根误差E表达式为：

(3)

均方根误差反映的是变量值与参考值之间的离散程度。

本文使用20CR V2c作为观测资料作为参考值，各模式对PNA(单位：m)/NPO(单位：hPa)模态(单位：m)的模拟结果作为变量值，对两套IPCC多模式集合进行泰勒图分析，以评估其对北太平洋大气环流主模态的模拟能力。值得注意的是，本文泰勒图统一使用标准化泰勒图，即对参考值与变量值的标准差与均方根误差同除以参考值的标准差，令参考值=1，E=0，并消除其物理量单位。

2.3.3 谱分析方法 周期性连续信号的频谱可表示为离散的非周期序列,它的幅度频谱的平方所排成的序列即为其功率谱。利用谱分析方法能够找到数据的相关特性。通常一个时间序列是以时间轴为参考基准进行记录的，直观上并不能获取数据内部的基本特性与周期规律。本文通过谱分析的方法，将时域转换到频域上，通过分析频域的特征来获取数据的周期特性。

为研究PNA与NPO的功率谱周期特性，本文对其EC(Expansion Coefficient)时间序列进行了功率谱分析。参考Furtado等[2]工作中对低频变率的北太平洋环流系统振荡(North Pacific Gyre Oscillation)的谱分析研究。首先构建出PNA与NPO各自的EC时间序列，使用EC时间序列的主要原因为PNA与NPO在冬季尤为显著，因此从GPH与SLP场截取DJF组成冬季连续场进行分析，然而谱分析当中，需要全年连续的时间序列，因此本文在做PNA与NPO的谱分析时，需要应用到EC时间序列。谱分析具体方法如下：

(1)利用GPH/SLP异常场获取PNA/NPO模态(模态获取的具体方法参考2.3.1)。

(2)再次利用GPH/SLP原始异常场(三维场)除以PNA/NPO模态(二维场)得到该模态的EC时间序列(一维场)。

(3)对PNA/NPO的EC时间序列做功率谱分析，一般功率谱纵坐标为功率，横坐标为频率。将功率-频率结果换算为功率-周期，取功率谱峰值超过90%信度的周期进行着色。

由于非负值的功率谱曲线所覆盖的面积在数值上等于其总功率(能量)，考虑到每个IPCC模式总功率可能各不相同，因此本文所有功率谱均使用标准化的功率，即各周期的功率值除以总功率，消除物理量单位，从而得到功率百分比以方便多模式之间的对比。

在谱分析方法第三步骤当中，使用的信度检验主要参考Torrence和Compo[27]的工作，其主要思想为先对PNA/NPO的EC时间序列构建一个适合的背景谱，然后根据F检验当中的90%信度的分布值乘以其背景谱，得到功率谱90%信度检验线。

3 对空间模态的模拟能力评估结果

本文选取20CR V2c再分析资料所提取的PNA/NPO模态作为泰勒图的参考值，对CMIP3/CMIP5两套多模式集合对其空间分布模拟能力进行综合评估与对比分析。图1表示观测资料所提取的冬季PNA模态，其主成分方差贡献率为29.8%，前人研究当中往往将PNA作为一个整体，并没有对其各异常中心进行分别命名。作为本文的创新点，本文分别统计其4个中心异常的变化情况，并对每个中心进行重新简化命名，按照其4个异常中心地理位置分布，自西向东依次命名为PNAa，PNAb，PNAc和PNAd，具体对应关系可参考图1。其中PNAb为PNA最强异常中心。其中心异常值的变化往往决定着PNA的变化，PNAb经常伴随气旋式海表面风异常与风应力异常，当中纬度西风加强时，北太平洋在中纬度将失去热量，而在北美西岸到阿拉斯加地区，由于受到埃克曼平流作用所造成的沿岸上升流的影响，海洋又将得到热量，由此得到一个PNAb上空对流的正反馈机制，而其高空对应西风急流出口区域，为辐散区，这使得对流会异常的强，强对流所导致的局地降水的增多，也会在高空大气释放潜热，通过非绝热加热来加热大气，会在北太平洋中纬度PNAb区形成一个较强的低压异常，从而影响整个PNA的变化。

图1 20CR V2c北太平洋500 hPa位势高度异常场的冬季PC1回归场(单位：m)Fig.1 Regression pattern of the 500 hPa GPHa onto the PC1 in wintertime at North Pacific from 20CR V2c

图2表示观测资料所提取的冬季NPO模态，其主成分方差贡献率为20.0%。作为北太平洋大气环流的第二主模态，同PNA一样，本文对NPO偶极子也进行了简化命名，根据其南北“跷跷板”式的偶极子异常的特殊结构，由北向南，依次命名为NPOa与NPOb。NPO表现为从海平面到对流层高层相似的垂直结构，NPOa对应气旋式的海表面风应力和风速异常，NPOb对应气旋式的海表面风应力和风速异常。

图2 20CR V2c北太平洋海平面气压异常场的冬季PC2回归场(单位：hPa)Fig.2 Regression pattern of the SLPa onto the PC2 in wintertime at North Pacific from 20CR V2c

为综合反映两套多模式集合的模拟效果，本文使用图1、图2所示的整个二十世纪的观测PNA(NPO)模态作为泰勒图中的参考值。两套多模式也同样使用对二十世纪大气模拟的情景(CMIP3：20C3M；CMIP5：Historical)，使用相同的时间段，对CMIP3/CMIP5模式的空间模拟能力进行评估。

3.1 PNA空间型模拟能力评估结果

首先本文通过2.3.1小节的方法获取CMIP3中21个模式与CMIP5中30个模式的PNA模态。因无特殊科学意义，这51个模态并未在本文附图。本文分别计算CMIP3与CMIP5各模式与观测PNA模态的相关系数，均方根误差与各自的标准差，并分别绘制CMIP3(见图3)与CMIP5(见图4)的模拟结果泰勒图。

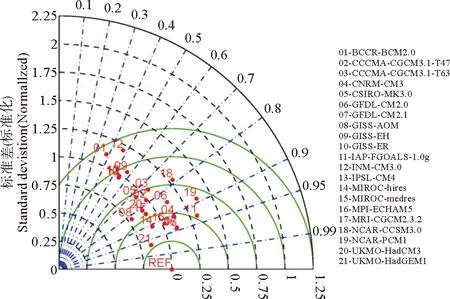
(图中黑色虚线代表标准差，刻度参考Y轴；蓝色点划线表示与观测资料的相关系数，刻度参考弧上刻度值；绿实线表示各模式与参考值间的均方根误差，刻度值位于X轴；REF为观测资料参考值；带序号红点为各模式所提取的PNA模态，模式名称及对应序号见图右列。Standard deviation and the centered pattern RMS difference are normalized by the observational standard deviation. Normalized standard deviation and spatial correlation coefficient of a model are given by the radial distance from the origin (black dashed line) and the azimuthal position of the model (blue dot-dashed line), respectively. The distance from the REF (i.e., observation) to a red point (i.e., a model) is the normalized CRMS (green solid line.).)

图3 CMIP3多模式对PNA模态模拟结果泰勒图
Fig.3 Taylor diagrams for displaying normalized pattern statistics of PNA in CMIP3 models

3.1.1 能力评估 利用图3与4的结果，设计统计表(见表1)。根据相关性显著原理，相关系数超过0.4则认为具有相关关系，超过0.7则表示具有较高的相关程度。由于本文为空间相关，格点数较多，为更好的体现各模式与观测间的关系，因此认为相关系数超过0.5为具有空间相似关系，而本文泰勒图全部进行了标准化以反映不同模式间的差异性，因此在观测值自身标准差(σ=1)附近，R=0.5对应E≈1，因此我们定义各模式模拟合格标准为R≥0.5，E≤1。同理良好标准为R≥0.8，E≤0.75；优秀标准R≥0.9，E≤0.5。

如图3所示，21个CMIP3模式名称列于泰勒图右侧，所对应的编号体现于泰勒图结果中，其模拟能力见表1，其中CCR-BCM2.0(R=0.38)和INM-CM3.0(R=0.47)模式对PNA模拟失败；86%的模式具有与观测相似的PNA幅度(标准差σ在1±25%范围内)，IAP-FGOALS-1.0g(σ=1.31)，NCAR-CCSM3.0(σ=1.28)与NCAR-PCM1(σ=1.37)模式所模拟的PNA幅度皆过大。表现优秀的6个模式为：CNRM-CM3，GFDL-CM2.1，MIROC-hires，MIROC-medres，MPI-ECHAM5，UKMO-HadGEM1。

图4 同上图，但是为CMIP5多模式对PNA模态模拟结果泰勒图Fig.4 As in fig.3, but for PNA in CMIP5 models

/%

而图4中，30个CMIP5模式有80%的模式能够模拟出于观测相似的空间结构(Rgt;0.8)，所有模式都成功模拟出PNA模态(Rgt;0.5)；90%的模式具有与观测相似的PNA幅度(σ在1±25%范围内)，BNU-ESM(σ=1.31)，CESM1(BGC)(σ=1.37)与NorESM1-M(σ=1.32)模式所模拟的PNA幅度皆过大。表1中模拟优秀的14个模式为ACCESS1.3，BNU-ESM，CanESM2，CESM1(CAM5)，CMCC-CESM，CMCC-CM，GFDL-CM3，GFDL-ESM2G，HadGEM2-AO，HadGEM2-ES，IPSL-CM5A-LR，MPI-ESM-LR，NorESM1-M，NorESM1-ME。

3.1.2 结果分析 就整体而言，CMIP3与CMIP5大部分模式能够很好的模拟出PNA模态的地理分布及其幅度，其中CMIP3中UKMO-HadGEM1(R=0.97,E=0.28)模式的对空间形态的模拟结果最佳，而CMCC-CESM(R=0.97,E=0.33)模式在CMIP5中最佳但仍不如UKMO-HadGEM1模式，CCCMA-CGCM3.1-T47(σ=0.99)，IPSL-CM4(σ=0.99)与MIROC-medres(σ=1.02)模式对PNA幅度的模拟最佳。

与CMIP3相比，CMIP5各项指标均更为优越，但是不同模式间的差异仍旧比较大，其相关系数从0.52(INM-CM4)到0.97(CMCC-CESM)，均方根误差从0.31(GFDL-CM3)到0.99(EC-EARTH)有57%的模式Elt;0.5。整体上，CMIP5各模式对PNA的模拟能力较好。

3.2 NPO空间型模拟能力评估结果

基本原理与步骤同上小节PNA模态相同，首先获取CMIP3中22个模式与CMIP5中32个模式的NPO模态，并分别绘制CMIP3(见图5)与CMIP5(见图6)的模拟结果泰勒图及其统计表(见表2)。

图5 同图3，但是为CMIP3多模式对NPO模态模拟结果泰勒图Fig.5 As in fig.3, but for NPO in CMIP3 models

3.2.1 能力评估 如图5所示，22个CMIP3模式中BCCR-BCM2.0(R=0.06)，GISS-EH(R=0.05)，INM-CM3.0(0.49)，UKMO-HadGEM1(0.01)模式对NPO模态模拟失败；64%的模式具有与观测相似的NPO幅度(标准差σ在1±25%范围内)，BCCR-BCM2.0，(σ=0.66)CCCMA-CGCM3.1-T47(σ=0.72)，CCCMA-CGCM3.1-T63(σ=0.67)，GISS-AOM(σ=0.62)，GISS-EH(σ=0.74)，GISS-ER(σ=0.74)，UKMO-HadCM3(σ=0.69)，UKMO-HadGEM1(σ=0.64)8个模式所模拟的NPO幅度皆过小。表现优秀的8个模式为：CSIRO-MK3.0，GFDL-CM2.1，IPSL-CM4，MIROC-hires，MIROC-medres，MIUB-ECHO-G，NCAR-CCSM3.0，NCAR-PCM1。

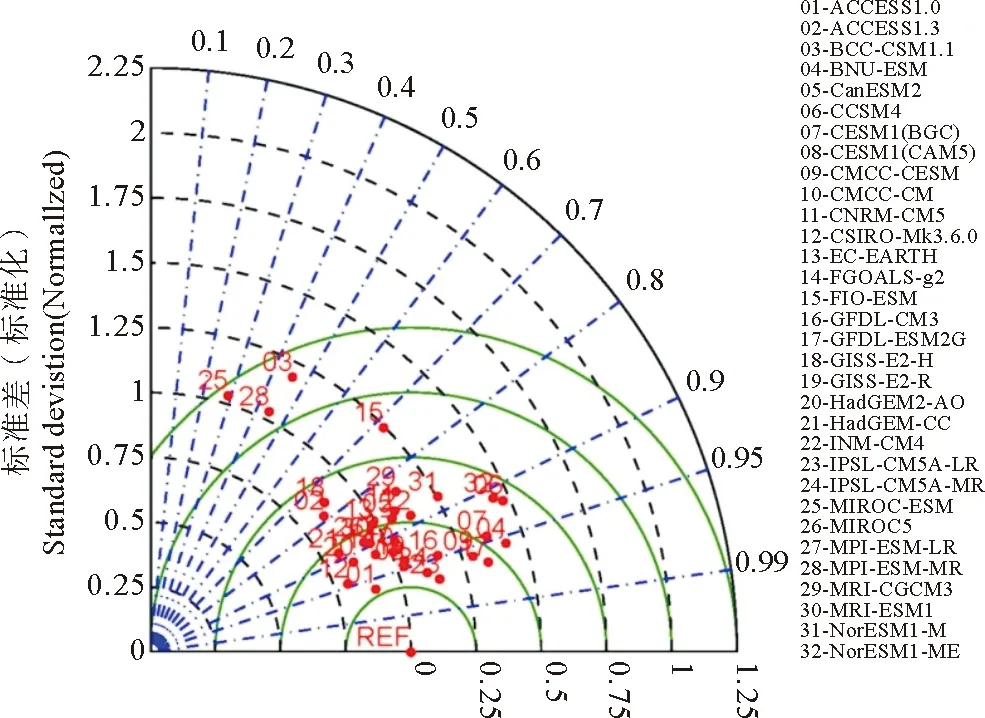
图6 同图3，但是为CMIP5多模式对NPO模态模拟结果泰勒图Fig.6 As in fig.3, but for NPO in CMIP5 models

如图6所示，32个CMIP5模式中BCC-CSM1.1，MIROC-ESM，MPI-ESM-MR三个模式没能成功模拟出NPO模态(Rlt;0.5)；78%的模式具有与观测相似的NPO幅度(σ在1±25%范围内)，BNU-ESM(σ=1.43)，CCSM4(σ=1.47)，CESM1(BGC)(σ=1.37)，CMCC-CESM(σ=1.29)，GFDL-ESM2G(σ=1.34)，NorESM1-M(σ=1.26)，NorESM1-ME(σ=1.44)7个模式所模拟的NPO变率过大，表现优秀的13个模式为：ACCESS1.0, CESM1(CAM5), CMCC-CESM, CMCC-CM, CSIRO-Mk3.6.0, FGOALS-g2, GFDL-CM3, GFDL-ESM2G, GISS-E2-R, HadGEM2-AO, IPSL-CM5A-LR, IPSL-CM5A-MR, MPI-ESM-LR。

以上模拟能力结果见统计表2。

表2 CMIP3/CMIP5模式评估结果统计表(NPO) /%

Note：①Excellent rate;②Good rate;③Failure rate

3.2.2 结果分析 就整体而言，CMIP3与CMIP5大部分模式能够很好的模拟出NPO模态的地理分布及其幅度，其中CSIRO-MK3.0(R=0.95,E=0.34)，MIROC-hires(R=0.95, E=0.32)，NCAR-CCSM3.0(R=0.96,E=0.35)，模式在CMIP3多模式集合中的对空间形态的模拟结果最佳，GFDL-CM2.1(σ=1.00)模式对NPO幅度的模拟最佳。

而CMIP5中ACCESS1.0(R=0.96,E=0.28)，CMCC-CESM(R=0.96,E=0.44)，GFDL-ESM2G(R=0.97,E=0.46)，IPSL-CM5A-LR(R=0.97,E=0.30)，IPSL-CM5A-MR(R=0.96,E=0.31)5个模式的对空间形态的模拟结果最佳，数量上要多于CMIP3模式，同CMIP3多模式一样，CMIP5不同模式间的差异也是比较大，其相关系数从0.29(MIROC-ESM)到0.97(IPSL-CM5A-LR)，均方根误差从0.28(ACCESS1.0)到1.21(MIROC-ESM)有50%的模式Elt;0.5。总的来说，CMIP5模式对NPO的模拟能力相对较好，各项指标均优于CMIP3模式。

4 对时间周期的模拟能力评估结果

本文评估CMIP3/CMIP5模式对PNA/NPO的时间模拟能力，是基于谱分析方法综合评估各模式对PNA/NPO的时间周期的模拟能力。

本文基于2.3.3节谱分析方法的内容，获得各模式所模拟的二十世纪PNA/NPO的EC时间序列，并对该序列进行功率谱分析。为综合反映两套多模式集合的模拟能力，本文设计了多模式标准化功率谱填色图(见图7)。从该图中，可以清晰的看到每个模式所模拟的PNA/NPO的周期及其所对应的标准化功率。将观测资料的功率谱置于第一行以方便下面多模式与其对比分析，此外本文还对该功率谱填色图做了进一步的统计分析，绘制与其对应的统计直方图(见图8)，并对PNA与NPO进行CMIP3与CMIP5的综合评估与对比分析。

4.1 对PNA周期的模拟评估

从图7与9中可以看到，观测资料与多模式的功率谱在一年周期内的季节尺度上存在较多峰值，表明PNA具有较多的不同周期的季节信号。本文重点关注其一年以上的年际信号与年代际信号。从观测资料中，可以看到PNA具有2个年际信号分别为1～2年周期与4～6年周期，以及一个广域周期的年代际信号，其峰值位于20～25年。根据以上PNA的周期特点，本文分别对CMIP3与CMIP5的多模式进行评估分析。

4.1.1 CMIP3结果 如图7，在21个CMIP3模式的功率谱中，可以看到UKMO-HadCM3与MRI-CGCM2.3.2两个模式完整的抓住了同观测相同的3个周期信号，其中UKMO-HadCM3刚好有3个同观测相同的周期信号，不过在年代际信号的模拟上，其周期要短于观测，峰值位于15年周期左右；而MRI-CGCM2.3.2模式在年际尺度上有4个周期信号，其中1～2年周期2个、3～5年周期1个、6～8年周期1个，其中对年代际信号的模拟其周期要长于观测，并且其整体标准化功率要大于观测，其峰值位于30年左右的周期上。除这两个模式以外，有33%(7/21)的模式能够抓到2个同观测相同的周期信号；有38%(8/21)的模式能够抓到一个周期信号且大部分抓住其1～2年的周期；而19%(4/21)的模式未能抓住任意一个同观测相同的周期，其中MIROC-medres在年际与年代际尺度上均无过信度的周期信号，IAP-FGOALS-1.0g在2～4年的周期上所表现的功率过于高。

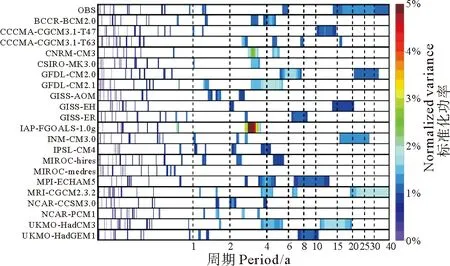
(横坐标为周期(单位：年)，纵坐标表示各模式(第一行OBS为观测值)，填色区代表其功率超过90%信度的部分，其标准化功率强度详见色带刻度。X-axis is for period (unit:year)；y-axis is for the models(first line shows the observation).Only significant power values(over 90% confidence level)are shaded.See colorbar for the normalized variance.)

图7 观测与CMIP3多模式中PNA的EC时间序列的标准化功率谱
Fig.7 Power spectra (% of total variance explained) of the EC time series of PNA for observations and CMIP3 historical simulations

从图8对多模式功率谱统计直方图来看，大部分的模式都能抓住其1～2年的周期，不过其平均功率峰值要小与观测。而有大部分模式也表征出其与之相近的2～4年周期，若按照1～4年的周期尺度来看，多模式的平均峰值同观测功率峰值一致，且90%(19/21)的模式能够抓住这个周期信号。对于其4～6年周期，有33%(7个)模式存在峰值，不过其功率强度都整体偏大与观测。峰值位于20～25年周期的模式仅有14%(3个)，不过具有年代际尺度的模式有33%(7个)，其功率强度都与观测相似。

整体来说CMIP3多模式数据集合中，能够完整体现同观测一致的PNA周期信号的模式很少，大部分模式能够正确表征PNA1～4年的周期，对4～6年的周期功率强度模拟的偏高，有一小部分模式正确模拟出PNA的年代际信号的周期与功率。

4.1.2 CMIP5结果 如图9，在30个CMIP5模式的功率谱中，可以看到ACCESS1.3，FGOALS-g2和GFDL-CM33个模式完整的抓住了同观测相同的3个周期信号，其中ACCESS1.3在2～4年周期上还存在一个信号，在年代际信号的模拟上，其周期为30～40年，要长于观测；而FGOALS-g2模式比其在CMIP3当中的FGOALS-1.0g模式有了长足的进步，在2～4年周期上，同样也存在一个信号，其中对年代际信号的模拟其周期要长于观测，并且其整体标准化功率要大于观测，其峰值位于30年左右的周期上；GFDL-CM3在2～4年周期上有3个信号，其年代际周期长度较短，为15年左右的周期。除这3个模式以外，有33%(10/30)的模式能够抓到两个同观测相同的周期信号；有43%(13/30)的模式能够抓到一个周期信号且大部分抓住其1～2年的周期；而13%(4/30)的模式未能抓住任意一个同观测相同的周期，其中MIROC5在4～10年的周期上所表现的功率过于高。

(横坐标为与上图对应的周期，纵坐标表示标准化功率，蓝条表示在观测值在其周期上的功率峰值， “*”表示各模式在该周期上过信度的功率峰值，红条表示所有“*”的平均值。Period in years is shown on the x-axis;normalized variance is shown on the y-axis;“*”denotes the model which has a peak in the specific bin;red bars are derived by averaging the “*”.)

图8 直方图为上图通过信度的峰值平均的统计图
Fig.8 Histograms of mean spectral peaks of the EC time series of PNA

从图10对多模式功率谱统计直方图来看，大部分的模式都能抓住其1～2年的周期，其平均功率峰值要小与观测，而有大部分模式也表征出其与之相近的2～4年周期，若按照1～4年的周期尺度来看，多模式的平均峰值同观测功率峰值一致，且87%(26/30)的模式能够抓住这个周期信号。对于其4～6年周期，有50%(15个)模式存在峰值，此结果要优于CMIP3，不过其功率强度都整体偏大与观测。而峰值位于20～25年周期的模式仅有7%(2个)，具有年代际尺度的模式有27%(8个)，其功率强度都与观测相似，虽然能够表征PNA年代际尺度的模式增多，但因为CIMP5多模式基数大，因此在对年代际的模拟上，整体反而不如CMIP3。

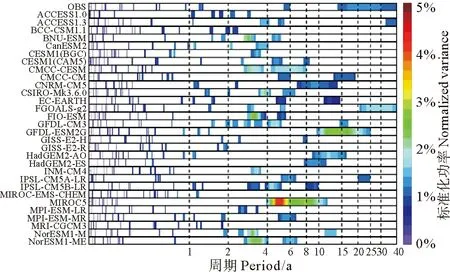
图9 同图7，但是为CMIP5多模式模拟PNA的EC时间序列的标准化功率谱Fig. 9 As in fig.7, but for EC time series of PNA in CMIP5 historical simulations

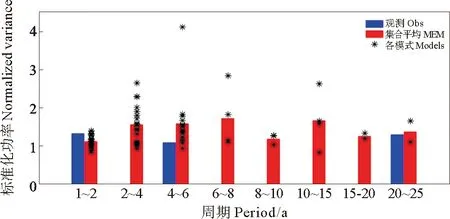
图10 同图8，但是为为上图通过信度的峰值平均的统计图Fig. 10 As in fig.8, but for PNA in CMIP5 models

综合来说CMIP5多模式数据集合中，能够完整体现同观测一致的PNA周期信号的模式很少，大部分模式能够正确表征PNA1～4年的周期，对4～6年的周期功率强度模拟的偏高，有一小部分模式正确模拟出PNA的年代际信号的周期与功率。以上结论基本与CMIP3中一致。

4.2 对NPO周期的模拟评估

从图11与13观测资料中可以看到NPO仅有一个2～4年的年际信号，其峰值位于2～3年。根据以上NPO的周期特点，分别对CMIP3与CMIP5的多模式进行评估分析。

4.2.1 CMIP3结果 如图11，在22个CMIP3模式的功率谱中，可以看到41%(9/22)的模式捕捉到其2～4年的信号，其中UKMO-HadCM3模式同观测模式一样有且仅有一个2～4年的年际周期，而有14%(3个)模式表现出15～25年的年代际信号，并且77%(17/22)的模式都表现出NPO1～2年的信号，少量模式反映其4～6与6～10年周期。

而从图12对多模式功率谱统计直方图来看，CMIP3模式对2～4年周期的模拟，在功率上还是要大于观测一些，整体来说CMIP3多模式数据集合中，将近一半模式能够体现同观测相同的2～4年周期信号，但对其功率强度模拟偏高。

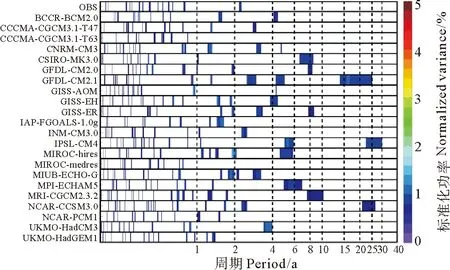
图11 同图7，但是为CMIP3多模式模拟NPO的EC时间序列的标准化功率谱Fig. 11 As in fig.7, but for EC time series of NPO in CMIP3 historical simulations

图12 同图8，但是为为上图通过信度的峰值平均的统计图Fig.12 As in fig.8, but for NPO in CMIP3 models

4.2.2 CMIP5结果 如图13，在32个CMIP5模式的功率谱中，可以看到44%(14/32)的模式捕捉到其2～4年的信号，其中GISS-E2-R与INM-CM4模式同观测模式一样有且仅有一个2～4年的年际周期，而有13%(4个)模式表现出年代际信号，并且84%(27/32)的模式都表现出NPO1～2年的信号，部分模式反映其4～6与6～10年周期。

从图14对多模式功率谱统计直方图来看，CMIP5模式对2～4年周期的模拟，在功率上还是要大于观测许多，整体来说CMIP3多模式数据集合中，将近一半模式能够体现同观测相同的2～4年周期信号，但对其功率强度模拟偏高。同CMIP3的结论类似，CMIP5多模式中，更多的模式表现出NPO在1～2年的年际周期信号。

5 总结与讨论

本文以20CR V2c资料所提取的二十世纪北太平洋大气环流模态作为观测参考值，利用泰勒图方法与谱分析方法，分别对PNA与NPO模态在CMIP3与CMIIP5两套多模式数据集合中的表现进行了从空间型到时间周期的综合评估与对比分析工作。因之前从未有人使用IPCC两次评估报告所评估的两套全球海气耦合多模式数据集(CMIP3与CMIP5)进行对PNA/NPO的模拟能力的评估，因此这也是本文的创新之处并且也具备实际应用价值的。本文另一个创新之处在于首次为PNA的4个异常中心以及NPO的2个偶极子进行简化命名，令我们所要表达的某个异常中心的描述更加明确，不易产生混乱的理解。

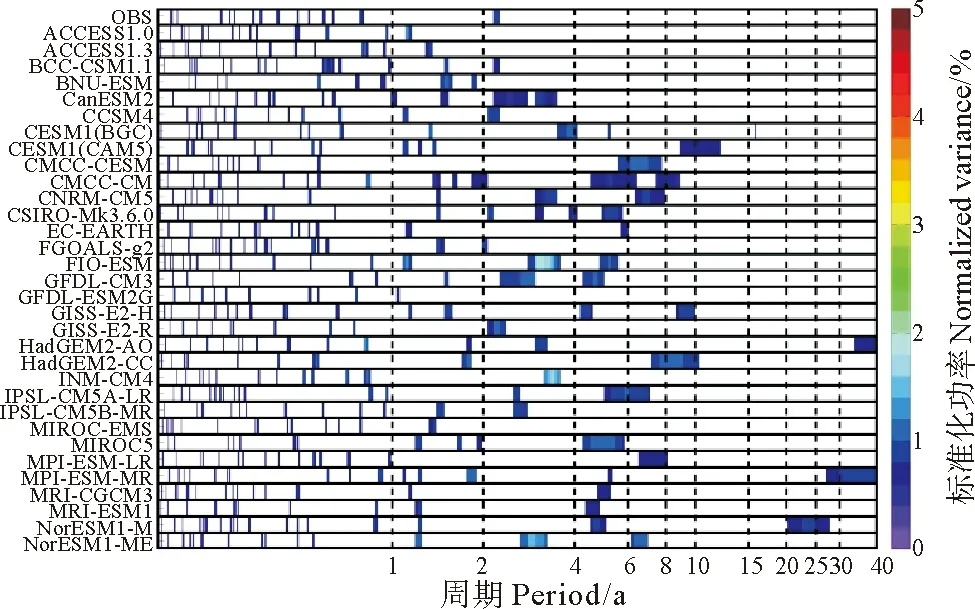
图13 同图7，但是为CMIP5多模式模拟NPO的EC时间序列的标准化功率谱Fig. 13 As in fig.7, but for EC time series of NPO in CMIP5 historical simulations

图14 同图8，但是为为上图通过信度的峰值平均的统计图Fig. 14 As in fig.8, but for NPO in CMIP5 models

本文对CMIP3与CMIP5在二十世纪PNA与NPO模态的空间模拟能力进行系统的评估，其结果表明：整体上CMIP5模式对PNA与NPO的空间型模拟能力要优于CMIP3模式，80%的CMIP5模式都能很好的体现与观测资料相近的北太平洋大气环流模态，而CMIP3模式只能达到约60%。在对PNA/NPO模拟优秀的模式上，CMIP5的优秀率也远高CMIP3约10%。若按照PNA与NPO进行划分，CMIP5模式整体对PNA的模拟要优于NPO，不过PNA作为北太平洋第一主模态，相对比较容易被模式捕捉到，而CMIP3模式对NPO对模拟两极分化比较严重，模拟较好的模式与模拟失败的模式都比模拟PNA模态的要多。两套模式本身都对PNA模态标准差模拟的偏大，而对NPO模态，CMIP3标准差整体偏小，而CMIP5整体偏大。

在使用谱分析方法对两套资料对时间模拟能力评估上，研究结果表明：在对时间的模拟能力方面，CMIP5相比于CMIP3并没有太大的进步，虽然CMIP5表现优异的模式数量比CMIP3的多，但是由于其基数大，从概率学讲，其成功的数量也会相对多，不过整体合格率与CMIP3持平。其中大部分模式能够很好的模拟出同观测一致的PNA 1～2和4～6年的年际周期，对其20～25年的年代际周期的模拟相对较差，而对NPO来说，大部分模式也都能体现1～4年的年际周期，不过更多模式的功率峰值都在1～2年周期上，而且只有约一半模式能够体现与观测相同的2～4年周期。不过多模式整体对NPO周期的捕捉能力，要优于PNA，不过NPO在观测当中仅有一段2～4年的年际周期，而PNA有3段周期，其中一个为年代际周期，而多模式对年代际周期的模拟通常不是太好，无疑加大了对PNA周期模拟的难度。

通过本文对CMIP3/CMIP5模式的模拟评估发现，IPCC两套多模式对空间型的模拟明显要优于对时间周期的模拟。在空间型的模拟上，CMIP5模式比CMIP3模式有了很大的提高，而在时间周期的模拟上，二者相差不大。通过模式评估，本文找到了对PNA/NPO模拟优秀的模式。使用这些模式对北太平洋大气环流模态进行分析，能够提高结果的可信度。对比评估可以反应出IPCC两套多模式数据集合模拟能力的异同，比较结果对改进模式有极为重要的启示意义。

致谢：感谢WCRP耦合模式工作小组所提供的CMIP模式数据。

[1] Stoner K, Hayhoe K, Wuebbles D J. Assessing general circulation model simulations of atmospheric teleconnection patterns[J]. J Climate, 2009, 22(16): 4348-4372.

[2] Furtado J C, Lorenzo E D, Schneider N, et al. North Pacific decadal variability and climate change in the IPCC AR4 models[J]. J Climate, 2011, 24: 3049-3067.

[3] Latif M, Barnett T P. Decadal climate variability over the North Pacific and North America: Dynamics and predictability[J]. J Climate, 1996, 9: 2407-2423.

[4] Di Lorenzo E, Schneider N, Cobb K M, et al. North Pacific Gyre Oscillation links ocean climate and ecosystem change[J]. Geophys Res Lett, 2008, 35: L08607. doi: 10. 1029/2007GL032838.

[5] Linkin M E, Nigam S. The North Pacific Oscillation-West Pacific teleconnection pattern: mature-phase structure and winter impacts[J]. J Climate, 2008, 21: 1979-1997.

[6] Wettstein J J, Wallace J M. Observed patterns of month-tomonth storm track variability and their relationship to the background flow[J]. J Atmos Sci, 2010, 67: 1420-1437.

[7] Lau N C. Variability of the observed midlatitude storm tracks in relation to low-frequency changes in the circulation pattern[J]. J Atmos Sci, 1988, 45: 2718-2743.

[8] Rogers J C. Patterns of low-frequency monthly sea-level pressure variability (1899-1986) and associated wave cyclone frequencies[J]. J Climate, 1990, 3: 1364-1379.

[9] Leathers D J, Yarnal B, Palecki M A. The Pacific/North American teleconnection pattern and United States climate. Part I: Regional temperature and precipitation associations[J]. J Climate, 1991, 4: 517-528.

[10] Nigam S. Teleconnections[M].//Holton J R, Pyle J A, Curry J A, eds. Encyclopedia of Atmospheric Sciences. London: Academic, 2003: 2243-2269.

[11] Croci-Maspoli M, Schwierz C, Davies H C. Atmospheric blocking: space-time links to the NAO and PNA[J]. Clim Dyn, 2007, 29: 713-725.

[12] Ge Y, Gong G. North American snow depth and climate teleconne- ction patterns[J]. J Climate, 2009, 22: 217-233.

[13] Harding K J, Snyder P K. The relationship between the Pacific-North American teleconnection pattern, the great plains low-level ket, and North Central US heavy rainfall events[J]. J Climate, 2015, 28: 6729-6742.

[14] Deser C, Phillips A S, Hurrell J W. Pacific interdecadal climate variability: Linkages between the tropics and the North Pacific during boreal winter since 1900[J]. J Climate, 2004, 17: 3109-3124.

[15] Chhak K C, Lorenzo E D, Schneider N, et al. Forcing of low-frequency ocean variability in the Northeast Pacific[J]. Journal of Climate, 2009, 22(5): 1255-1276.

[16] Wallace J M, Gutzler D S. Teleconnections in the geopotential height field during the northern hemisphere winter[J]. Mon Weather Rev, 1981, 109: 784-812.

[17] Walker G T, Bliss E W. World weather V[J]. Mem Roy Meteor Soc, 1932, 4: 53-84.

[18] Christensen J H, Kanikicharla K K, Marshall G, et al. Climate phenomena and their relevance for future regional climate change[J]. ProgressusInquisitiones De Mutatione Climatis, 2013.

[19] Compo G P, Whitaker J S, Sardeshmukh P D, et al. The Twentieth Century Reanalysis Project[J]. Quarterly Journal of the Royal Meteorological Society, 2011, 137(654): 1-28.

[20] Compo G P, Whitaker J S, Sardeshmukh P D, et al. Intercom Parison of an Improved 20th Century Reanalysis Version 2c Dataset Spanning 1850 to 2012[C]. USA: AGU Fall Meeting, 2014.

[21] Baxter S, Nigam S. Key role of the North Pacific Oscillation-West Pacific Pattern in generating the extreme 2013/14 North American winter[J]. Journal of Climate, 2014, 28(20): 8109-8117.

[22] Khouakhi A, Villarini G. On the relationship between atmosph- eric rivers and high sea water levels along the U. S. West Coast[J]. Geophysical Research Letters, 2016,43(16): 8815-8822.

[23] Lou J, Zheng X, Frederiksen C S, et al. Simulated decadal modes of the NH atmospheric circulation arising from intra-decadal variability, external forcing and slow-decadal climate processes[J]. Climate Dynamics, 2107,48(7): 2635-2652.

[24] Solomon S. Climate Change 2007 : The physical science basis : contributionof Working Group I to the Fourth Assessment Report of theIntergovernmental Panel on Climate Change[C].USA: Intergovernmental Panel on Climate Change, 2007: 710-719.

[25] Taylor K E, Stouffer R J, Meehl G A. An overview of CMIP5 and the experiment design[J]. Bulletin of the American Meteorological Society, 2011, 93(4): 485-498.

[26] Taylor K E. Summarizing multiple aspects of model performance in a single diagram[J]. Journal of Geophysical Research Atmospheres, 2001, 106(D7): 7183-7192.

[27] Torrence C, Compo G P. A practical guide to wavelet analysis[J]. Bulletin of the American Meteorological Society, 1998, 79(79): 61-78.

责任编辑 庞 旻

TheAssessmentofNorthPacificAtmosphericCirculationPatternsBasedonCMIP3andCMIP5Models

CHEN Zheng1,2， GAN Bo-Lan1,2， WU Li-Xin,1,2

(1. The Key Laboratory of Physical Oceanography, Ministry of Education, Ocean University of China, Qingdao 266003, China; 2.Qingdao National Laboratory for Marine Science and Technology, Qingdao 266003, China)

Based onNOAA-CIRESTwentieth-Century Reanalysis dataset version 2c(20CR V2c) data, the North Pacific Atmospheric Circulation Patterns at twentieth century have been captured as for observational reference. By using Taylor diagram and spectrum analysis, thespatiotemporal features ofPacific-North American teleconnection (PNA) and North Pacific Oscillation (NPO) in twentieth century simulations are evaluated among Coupled Model Intercomparison Project Phase 3 (CMIP3)/CMIIP5 models, and also, the simpler name for each PNA (NPO) quadrupole (dipole) is defined.Analysis reveals that while the 80% of CMIP5 models and 60% of CMIP3 models reasonably simulate either the geographical distribution or the amplitude of PNA/NPO pattern. As for excellent models in spatial simulations, CMIP5 models are 10% more than CMIP3’s. As for the temporal featuresanalyzed by power spectrum,CMIP5 models show little improvement.Most models simulate the 1～2 years and 4～6 years interannualvariabilities of PNA, qualitatively consistent with the observation, whereas models generally lack the capability to reproduce the decadal (20～25 years) variability of PNA.And for NPO, most models show 1～2 years interannualperiod, only half of the models can simulate 2～4 years period which consistent with the observation.

Pacifical-North Ameaica Teleconnection(PNA)；North Pacific Oscillation(NPO)；Taylor diagram； spectrum analysis

P732.6

A

1672-5174(2018)01-001-11

10.16441/j.cnki.hdxb.20170085

陈峥， 甘波澜， 吴立新.基于CMIP3与CMIP5模式对北太平洋大气环流模态的评估分析[J].中国海洋大学学报(自然科学版), 2018, 48(1): 1-11.

CHEN Zheng， GAN Bo-Lan， WU Li-Xin.The assessment of North Pacific atmospheric circulation patterns based on CMIP3 and CMIP5 models[J].Periodical of Ocean University of China, 2018, 48(1): 1-11.

国家自然科学基金项目(41521091；41490643；41490640)资助

Supported by the National Natural Science Foundation of China(41521091; 41490643;41490640)

2017-02-29;

2017-03-29

陈 峥(1989-)，男，博士生。E-mail:chenzhengouc@163.com