考虑剪胀效应的边坡堆载稳定性研究

符碧君

（景德镇玉田水库管理处，江西景德镇 333000）

1 概况

边坡在堆载作用下产生的变形反应与边坡的多种性质相关[1,2]，譬如：堆载大小、边坡材料以及变形发展阶段等。针对不同的材料，边坡的变形比较复杂，其中包括边坡受到剪切力时，在剪切变形过程中出现的剪胀现象。对于研究边坡的安全系数，其主要考虑的材料参数为粘聚力C、内摩擦角φ以及剪胀角ψ，同时在计算过程中的屈服准则也应该考虑。如今，学者对于计算中的剪胀角处理方法主要有两种[3-6]：1）关联流动法则，即将材料的内摩擦角φ认为与剪胀角ψ相等；2）非关联流动法则，即认为材料的剪胀角ψ为零。上述2种处理方法，在使用过程中较为极端。一种将边坡材料的剪胀效果过度放大，而另一种基本忽略材料的剪胀角所带来的影响。鉴于此，有学者开始对剪胀角对边坡安全系数的影响进行研究。研究方法包括，研究其屈服准则、泊松比、非流动法则等对边坡稳定性的影响[7-10]，但是，对在堆载边坡下的安全系数与剪胀角之间关系方面的研究较少。

下文利用有限元软件及有限元强度折减法，对施加有堆载的边坡进行安全系数计算，同时考虑边坡材料有剪胀角影响，对比分析堆载边坡的安全系数随着不同剪胀角取值的剪胀效应，并为实际工程中的剪胀角取值提供一定的参考意义。

2 有限元分析方法及屈服准则

2.1 强度折减法

有限元强度折减法最早由Zienkiewicz提出，目前在岩土界被广泛使用。其方法为：通过对边坡岩土体材料参数进行一定的折减，主要是针对材料参数的粘聚力以及内摩擦角，再对边坡进行有限元迭代，直到计算出该边坡为临界破坏时，对应的折减系数的数值，最后将该数值作为边坡的稳定安全系数[9]。强度折减法对边坡材料的折减公式：

式中：Ki——强度折减系数；C——模型计算前的初始粘聚力的值；φ——模型计算前初始内摩擦角的值；Ci——模型进行强度折减后粘聚力的值；φi——进行强度折减完成后内摩擦角的值。

2.2 考虑剪胀角的Mobr-Coulomb屈服准则

根据不少学者对有限元强度折减法的深入认识，发现其在对安全系数求解过程中具有一定的缺陷性——材料参数的选取，提出考虑材料参数中的剪胀角影响。鉴于此，该文采用一种考虑映入材料剪胀角（即材料在受到剪力时出现塑性变形）的应变比：

对于摩尔—库伦屈服准则可以采用应力张量以及应力偏张量分别表示为：

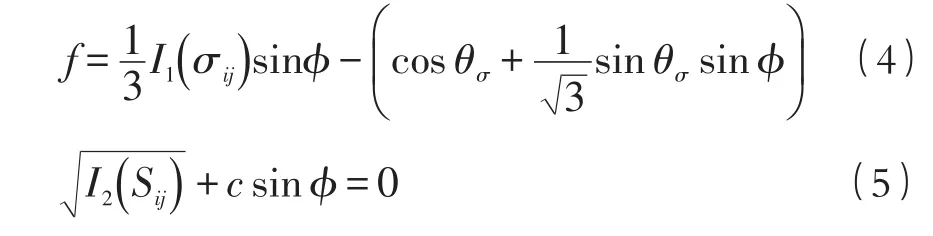
式中：I1(σij)——应力张量中的第一不变量；I2(Sij)——应力偏张量中的第二不变量；c——为黏聚力；θσ——应力Lode角度。

同时采用非关联流动法则，即Q≠f，计算过程中采用两者采用同一种形式，遂可以在式中进行Ψ与φ的互换，得到下式：

对式（6）（7）进行相互简化，可得：

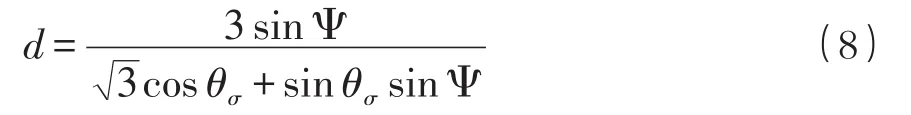
将式（6）中Q在最小值时所对应的Lode角θσ值带入至式（8）并简化得：

同时根据引入剪胀角后的广义Mises屈服准则，两者最后进行相应的简化与匹配，最后应用于实际有限元计算中。

3 有限元计算

在有限元软件Midas GTS-NX中建立简易的均质加载边坡模型，具体的模型几何尺寸及边坡模型荷载Q加载位置的简化模型，见图1。对于均质边坡模型的材料参数具体如下：重度γ，取值为20 kN/m3；粘聚力，c取值为30 kPa；内摩擦角 φ，取值为20°；弹性模量，E取值为10 MPa；以及材料的泊松比 μ，取值为0.30；荷载Q为均布荷载，其取值为20 kN/m。

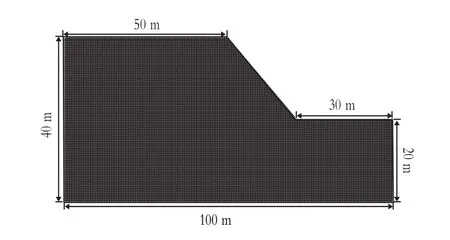
图1 简化模型

边坡模型的约束采用坡底边界约束其水平和竖向位移，而边坡模型的左右两边约束其水平位移，其余边界采用自由约束。

4 分析与讨论

为研究在堆载情况下对均质边坡安全系数的影响，通过有限元软件进行计算内摩擦角不变（φ=20°）的情况下，改变剪胀角的大小（0°，2°，…，18°，20°），并运用上述的屈服准则进行计算安全系数。堆载边坡在不考虑剪胀角时，采用强度折减法计算其安全系数为1.351。在考虑剪胀角时，均质堆载边坡的剪胀角与安全系数的关系，见图2。

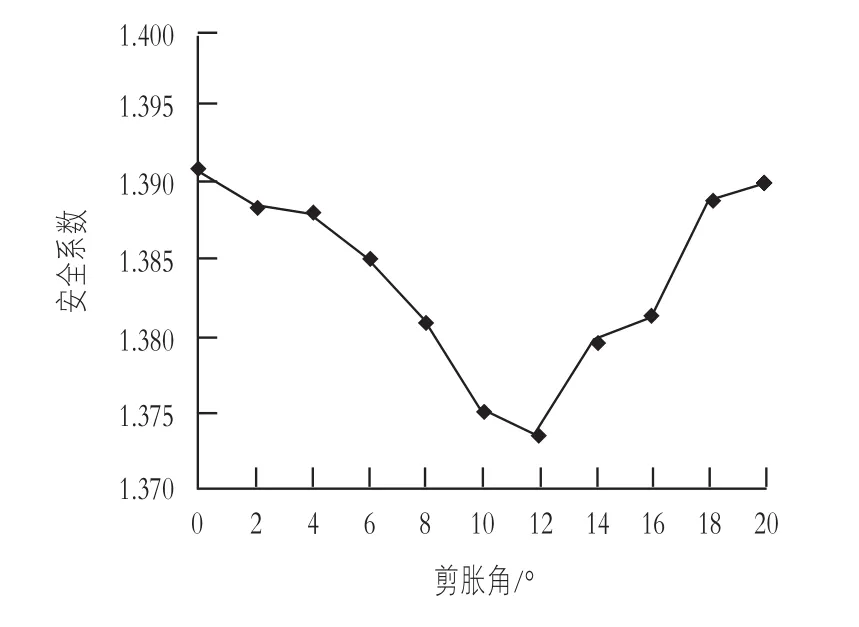
图2 剪胀角与安全系数的关系

由图2可知，边坡在考虑剪胀角时，其安全系数随着剪胀角的增加呈现出先减小后增大的趋势，并且剪胀角在1/2内摩擦角范围处达到安全系数的最小值。

考虑剪胀角堆载边坡失稳时位移矢量图，见图3。可以看出，随着剪胀角的增加，失稳时边坡的位移矢量图越明显，最大位移逐渐减小；随着剪胀角的增加，最大位移区域逐渐向坡脚移动。

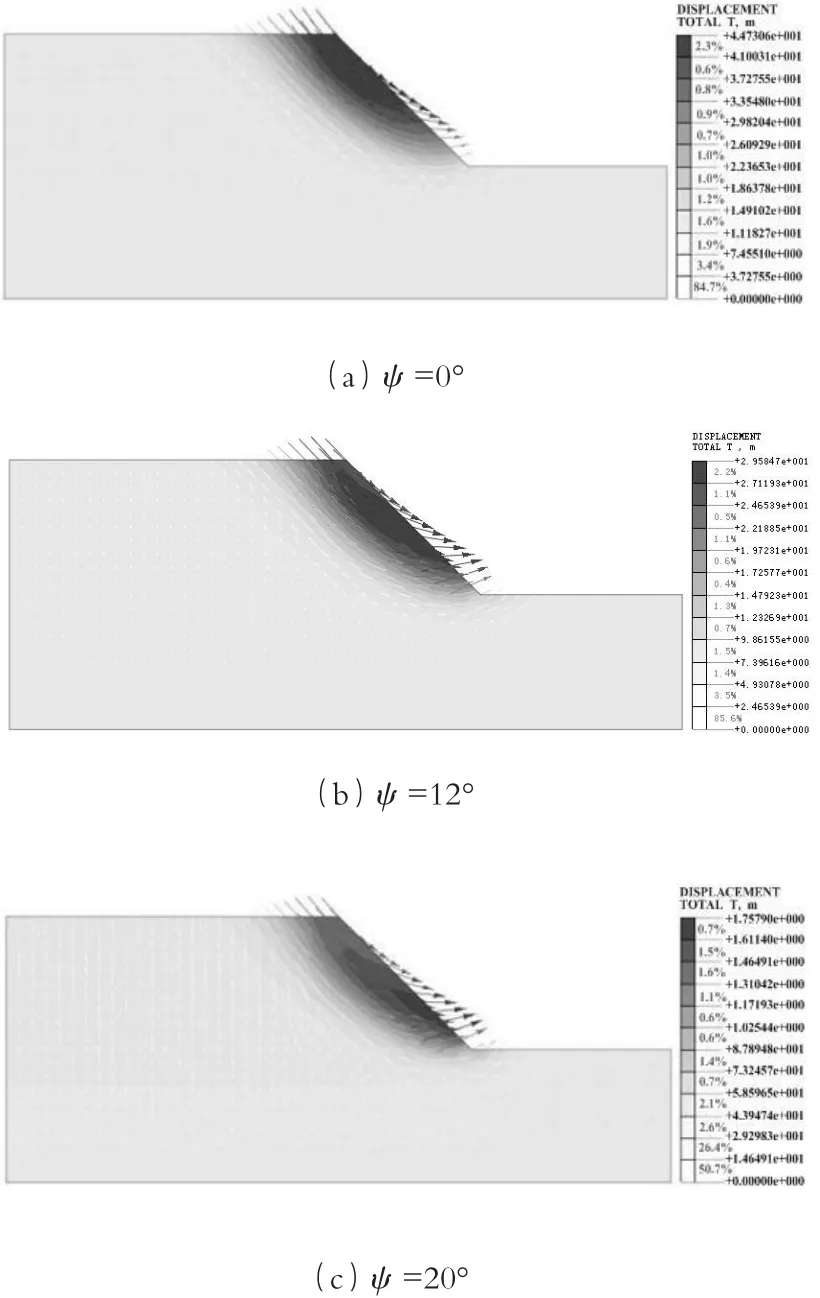
图3 考虑剪胀角失稳时位移矢量图

不考虑剪胀角堆载边坡失稳时位移矢量图，见图4。可以看出，不考虑剪胀角时边坡位移矢量图与ψ=20°（ψ=φ）时的矢量图基本相同，但其产生的位移更大。根据计算可得，计算安全系数过程中考虑剪胀角与不考虑剪胀角之间的最大误差为3.90%（ψ=0°时）。

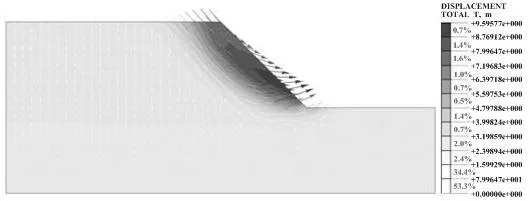
图4 不考虑剪胀角失稳时位移矢量图

5 结论

1）通过有限元强度折减法计算考虑剪胀角的边坡模型安全系数可得，随着剪胀角的增加，其安全系数先减小后增加；并且剪胀角在1/2内摩擦角范围处，其安全系数达到最小。

2）在计算边坡失稳时的位移矢量过程中发现，剪胀角越大其位移矢量越往坡脚处移动。

3）不考虑剪胀角时，边坡位移矢量与ψ=φ时的位移矢量图相同，但产生的位移值更大，两者安全系数最大误差为3.90%。