配电网谐波量测装置最优配置方法

李 炜， 仉志华， 隋国正， 孙 东， 曲泽奇

(1. 中国石化股份胜利油田分公司技术检测中心，山东 东营 257000; 2. 中国石油大学(华东)信息与控制工程学院，山东 青岛 266580; 3. 胜利油田河口采油厂，山东 东营257200)

0 引言

近年来，为实现节能减排与生产工艺灵活调整要求，油田电网中变频器等非线性电力电子设备日益增加，且有随机接入系统的网电钻机、网电修井机等设备，导致油田电网谐波源数量和类型不断增加，谐波分布日趋复杂。谐波含量超标易造成补偿电容器无法投入甚至爆炸、谐波谐振以及保护误动作等问题，直接影响油田供电系统的安全可靠运行。所以，研究油田电网中谐波产生的机理、总结在油田生产设备中典型谐波源发生特性，分析谐波产生的影响十分必要。谐波在线监测系统为分析和掌握油田电网谐波发射与传递规律，提供了有效手段。谐波量测装置费用高昂，从经济角度考虑不可能所有节点全部安装。同时，谐波状态估计的可观性和估计精度与量测量的数量、性质、位置以及系统网络的拓扑结构密切相关。

Heydt等人提出利用系数矩阵最小条件数法进行谐波量测配置优化[1],但此法仅能得到保证量测方程有解的最小量测点数量，没有涉及可观性等。文献[2]提出了关联矩阵可以判断可观测性，但未给出具体方法。文献[3]利用增广关联矩阵判断系统可观测性，且说明了冗余度对谐波状态估计精度的影响，但其状态量需要多次搜索，运算量大。文献[4]提出了逻辑判断法判断可观性，但只能判断电流量测支路对侧节点的可观性。文献[5]利用了网络拓扑分析可观性的方法，但其默认支路量测与节点电压量测分离，运算量大，不适合现有装置。

本文在文献[5]的基础上，一方面利用谐波量测装置可以测量节点电压及相关联的所有支路电流的特点，改进了可观性分析的算法，提高了运算效率；另一方面，引入可观测度与冗余度的概念，达到了提高谐波状态估计可观测度与精度的目的。

1 谐波状态估计基础理论

谐波量测装置量测量为节点电压、支路电流和节点注入电流，状态量为节点电压。在电网络的拓扑结构、支路参数以及量测装置安装布局已知的条件下，谐波状态估计表达式为[6-7]：

Z=HX+ε

(1)

式中：Z为量测量，通过量测装置直接读取；H为量测方程，与线路的拓扑结构、线路的参数以及量测装置的安装布点有关；ε为量测误差；X为要求解的状态量。量测方程表示量测量与状态量之间的关系，由以下三部分构成：

(1) 电压量测方程：

Vm,i=IVT,i

(2)

式中：Vm,i为节点i谐波电压量测量；VT,i为节点i谐波电压状态量；I为适当维数的单位矩阵。

(2) 节点注入量测方程：

(3)

式中：Im,i为节点i谐波注入电流量测量，中间节点的谐波注入电流值为0；VT,j为节点j谐波电压状态量；yi,j为节点导纳矩阵中对应节点i和j的分块导纳矩阵元素；n为网络节点总数。

(3) 支路量测方程：

Ii,j=Yi,j(Vi-Vj)

(4)

式中：Ii,j为节点i到j之间支路的电流；Vi和Vj为节点i和节点j的节点电压；Yi,j对应节点i和j之间的导纳矩阵。

2 谐波状态估计的可观性逻辑判断方法

谐波量测配置理论基于谐波状态估计可观性分析。可观性分析就是在已知系统网络拓扑结构和量测装置配置的基础下，通过利用量测装置提供的数据来确定未知节点状态的能力[8-9]。若基于量测装置提供的数据通过量测方程能够得出整个系统节点的电压或电流相量，即通过对系统状态估计可以使系统各节点状态已知，此时系统网络视为完全可观。若基于量测装置提供的数据通过量测方程不能得到整个系统的节点电压或电流相量，则此时系统网络不可观或不完全不可观。

谐波状态估计的可观性逻辑判断方法主要基于前文的3类量测方程。由于谐波量测装置不仅可测所安装节点的电压，还可测与该节点相关联的所有支路的电流，因此谐波状态估计的可观性有下列特点[10-14]：

(1) 若节点存在量测装置，则该节点的状态完全可观；(2) 在本侧节点电压可观时，支路电流量测使与该量测支路互联的对侧节点的状态可观；(3) 若某支路两端的节点电压均可观时，则该支路的电流可观；(4) 若某节点无可疑谐波源，且该节点没有配置量测装置，若该节点相连所有支路电流仅有一个未知，则可根据基尔霍夫电流定律对该支路电流进行求解，该支路电流可观。

可见，当量测配置选在包含支路关联关系最多的节点时，其可观的范围最大。

3 量测配置优化方法

量测装置的优化布点根据优化目的的不同，大体可以分为几类：(1) 出于经济性考虑，配置最少的量测装置，达到最大程度的可观。(2) 配置较少的量测装置，优先考虑使谐波状态估计达到一定精度，其次达到最大程度的可观。(3) 配置一定的量测装置，优先考虑达到最大程度的可观，其次使谐波状态估计达到一定精度。

系统可观测范围可由可观测度表示，可观测度[15]是指可观测的节点数与电网络中总节点数的比值，可观测度为1则表示系统完全可观。同时在可观的情况下，考虑系统的冗余度，冗余度[15]为量测点被重复测量的次数。文中量测装置的优化布点，是通过配置一定数量的量测装置，使其达到系统的最大可观，当不同量测配置方案的可观性一致时，优先选择冗余度最大的方案。

根据谐波状态估计可观性的特点，文中将节点的可观性分为直接可观和间接可观[16-22]。直接可观判断依据可观性特点(1)、(2)、(3)，通过关联矩阵进行一次运算即可判断；间接可观判断依据可观性特点(4)，须对关联矩阵进行二次运算得到。综上，量测配置优化分为2个步骤：

(1) 直接可观节点判断。以系统的可观测度为目标，假设系统的节点数为n，有k个量测配置方案，建立量测装置的优化布点函数：

(5)

通过此步骤，可以判断出每种量测配置方案下除本身装有量测装置的节点外直接可观的节点，即新增直接可观节点，以及各直接可观节点重复测量的次数即冗余度。

(2) 间接可观节点判断。对于第i个量测配置方案下新增的直接可观节点m，有：

fm=Am-Xi

(6)

式中：Am为关联矩阵的第m行，表示m节点与各节点之间的关联关系；Xi为第i种量测配置方案。

若fm中，除第m列外，仅有一列元素为1，则该列对应节点可观，Fi中该列元素加1；对各量测配置方案的所有新增直接可观节点重复执行步骤(2)。

完成所有步骤后，分析F中的每一行(即每种量测配置方案)的元素，对每种量测配置方案下的可观测度和冗余度进行比较，选择可观测度最大的量测配置方案为最优配置方案，若有多个量测配置方案可观测度同时最大时，选择冗余度最大的量测配置方案。上述过程流程图如图1所示。

图1 量测配置优化流程Fig.1 Flow chart of measurement configuration optimization

4 算例分析

本算例以胜利油田河口采油厂大一变电所某馈线为研究对象，在线路上选取节点布置量测装置。对该线路模型进行简化，简化图如图2所示。根据线路模型简图，关联矩阵A如下：

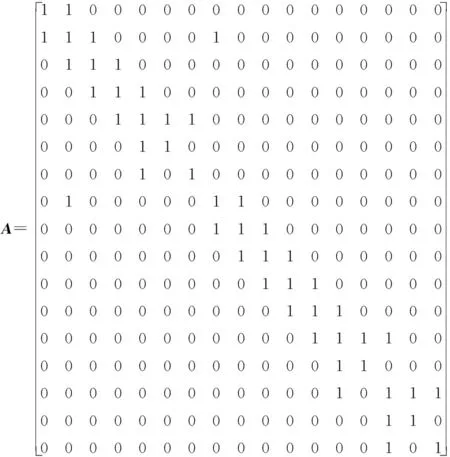
图2 线路模型简化图Fig.2 Simplified schematic of Oilfield distribution network line

(1) 当量测装置数量分别为3和4时，对关联矩阵进行可观性分析，得到量测配置优化布点结果如表1所示。从表1中可以看出，当量测装置数目为3时，共有2种配置方案可供选择，2种策略可观测度和冗余度相同，均为系统部分可观且达到系统最大可观测度，且量测冗余度均为0，可根据油田现场实际情况选择合适的配置方案；当量测装置数量为4时，共有3种配置方案可供选择，系统最大可观测度达到0.882 353，且量测冗余度均为0。

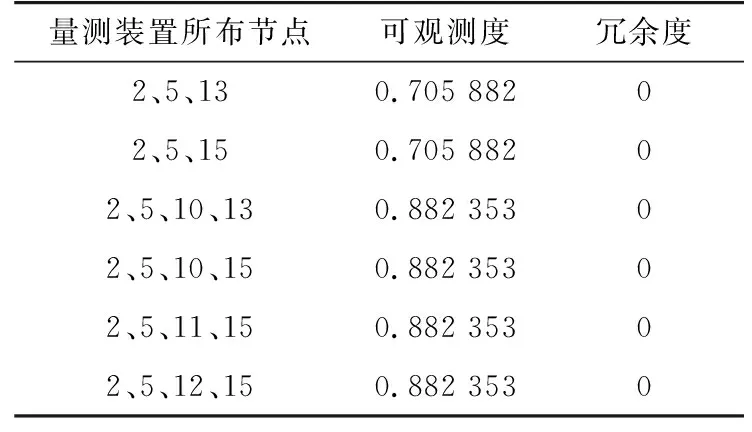
表1 量测装置布点方案Tab.1 Measuring device layout scheme

(2) 当量测装置数量为5时，利用关联矩阵进行可观性分析，量测配置优化布点结果如表2所示。

表2 考虑系统可观测度最大的量测优化布点方案Tab.2 Optimized layout scheme considering the maximum observability of the system

由表2可以看出，当量测装置数量为5时，系统可以达到完全可观的布点方案有6种，但其冗余度并不相同，此时，从状态估计精度角度考虑，选择冗余度最大的方案，即方案Ⅰ与方案Ⅲ。

由于油田现场实际情况复杂，有些节点施工难度高，不便于安装量测装置，且不同节点负载特性不同，因此可适当选择量测配置方案。

(3) 当量测装置为5时，采用表2中方案Ⅰ作为谐波量测装置配置方案，进行谐波状态估计，以5次谐波为例，量测量如表3、4所示，表4中支路编号“2—1”指节点2与节点1之间支路编号，支路电流量测方向为节点2指向节点1，其他支路同理。状态估计结果如表5所示，其中误差指估计值相对于仿真值的误差。

表3 节点电压量测量Tab.3 Measurement of node voltage

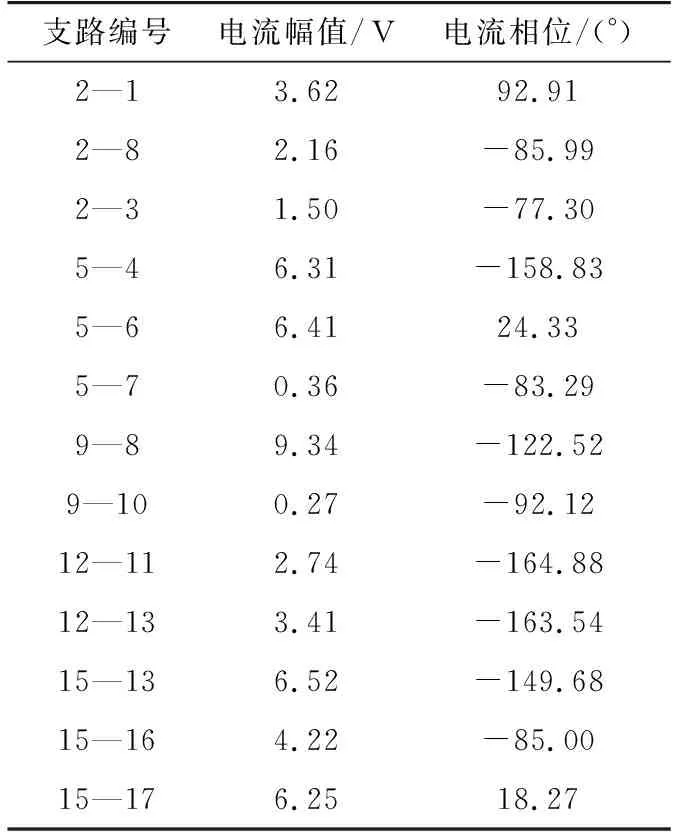
表4 支路电流量测量Tab.4 Measurement of branch current

表5 5次谐波电压幅值和相位误差对比Tab.5 5th harmonic voltage amplitude and phase error comparison

可以看出，根据表2的方案Ⅰ，系统达到了完全可观，且精度较高，误差较小。

5 结语

由于油田配电网网络拓扑结构复杂，节点支路众多，谐波源分布不规律，较为分散，使得谐波状态估计量测装置配置不要求实现全局可观。本文的量测装置最优配置方法，在给定量测装置数量的情况下，可以实现最大程度的可观。且本方法通过关联矩阵进行计算，由于关联矩阵的稀疏性，使得量测装置配置原则简洁明了。当不同的量测装置配置方案可观测度相同时，优先选取量测冗余度最大的量测装置配置方案，提高状态估计的精度。并针对胜利油田河口采油厂大一变电所某馈线进行量测装置配置优化，分别给出了当量测装置数目为3、4、5时的量测装置配置方案，并根据配置方案，给出了量测装置数目为5时的谐波状态估计结果，结果表明系统达到完全可观，且误差较小。算例验证了本方法的有效性。